다이나믹 프로그래밍 (DP)

📑 정의

하나의 문제는 단 한 번만 풀도록 하는 알고리즘이다. 한 번 푼 것을 여러 번 다시 푸는 비효율적인 알고리즘을 개선시키는 방법이기도 하다.

일반적으로 상당수 분할 정복 기법은 동일한 문제를 다시 푼다는 단점을 갖고 있다.

• 다만 분할 정복 기법은 "정렬" 과 같은 몇몇 요소에 대해서는 동일한 문제를 다시 풀게 되는 단점이 없다.
  예를 들어 1~7을 정렬해야할 때 1~3/4~7 나눠서 정렬하고 다시 합하면 서로 1~3, 4~7 서로 다른 문제이기 때문에 중복이 없어 문제가 되지 않는다. 대표적으로 큌 정렬이나 병합 정렬은 매우 빠르다.

단순 불할 정복으로 풀게 되면 심각한 비효율성을 낳는 대표적인 예시가 바로 피보나치 수열이다.
피보나치 수열은 특정한 숫자를 구하기 위해 그 앞에 있는 수자와 두 칸 앞에 있는 숫자의 합을 구해야한다.

🧫 예시

피보나치 수열의 점화식: D[i] = D[i-1] + D[i-2]

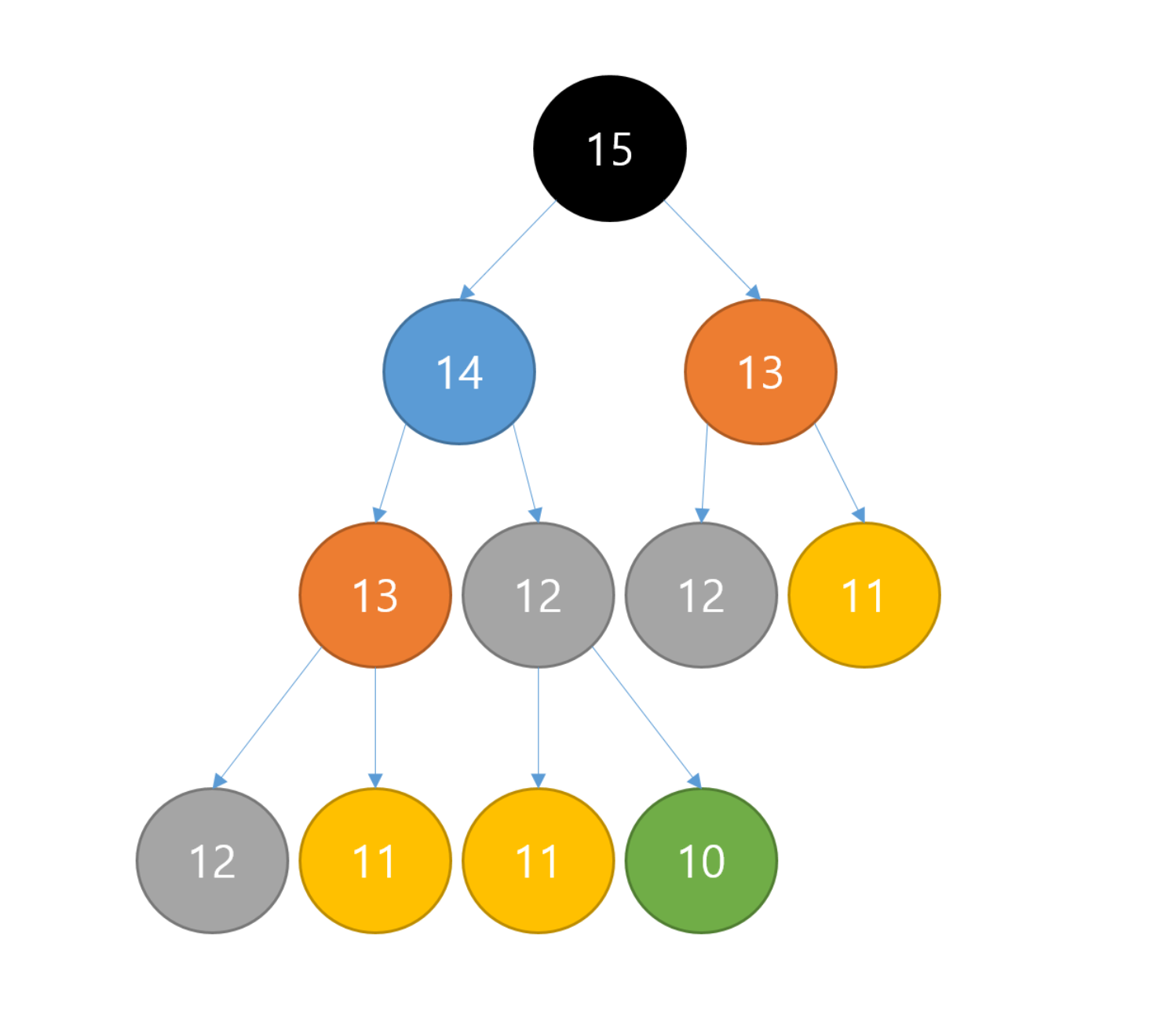
만약 단순 분할 정복 기법을 사용해 15번 째 피보나치 수열을 구한다고 가정한다면 위 사진을 봤을 때 동일한 노드들이 여러 번 반복되는 것을 확인할 수 있다.
이렇게 불필요하게 12 라는 수가 여러번 반복적으로 계산될 것이다. 따라서 이런 불필요한 연산을 줄이고자 동적 프로그래밍 기법을 사용해야 한다.

다이나믹 프로그래밍은 다음의 가정 하에 사용할 수 있다.

1. 큰 문제를 작은 문제로 나눌 수 있다.
2. 작은 문제에서 구한 정답은 그것을 포합하는 큰 문제에서도 동일하다.

불할 정복 기법 예제 코드

public class DivideConquer {
    public static void main(String[] args) {
        int q = 10;
        int answer = divideConquer(q);
        System.out.println("피보나치 " + q + " 은 " + answer);
    }

    public static int divideConquer(int x) {
        if (x == 1) return 1;
        if (x == 2) return 1;
        return divideConquer(x - 1) + divideConquer(x - 2);
    }
}

만약 이 10을 50으로 바꾼다면 굉장히 오래걸리는데 이 50을 얻기위해 실행될 연산 횟수를 구해보자.
대충 계산해보면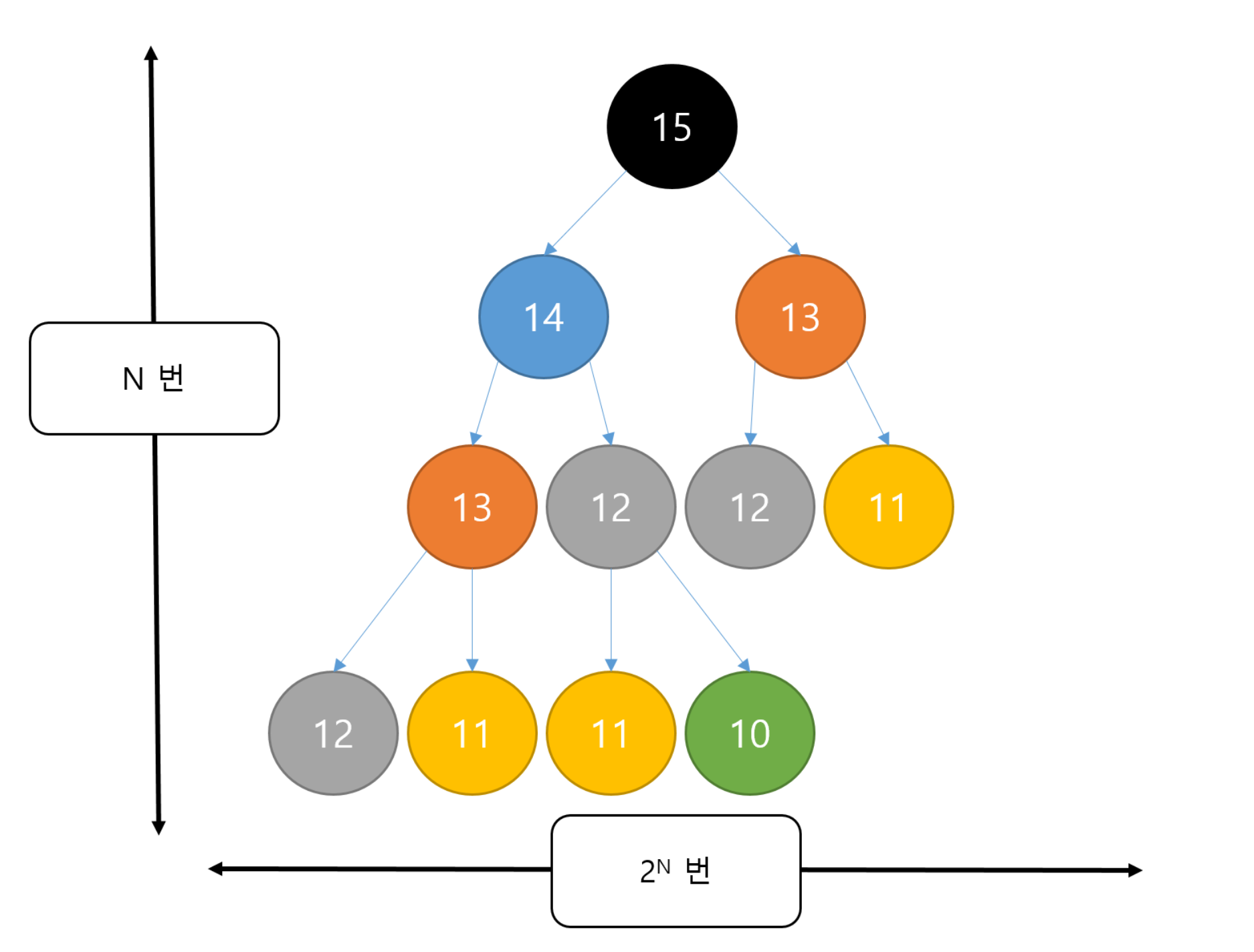
2의 50 승 즉, 대충 2^10 을 1000 이라 놓고 0이 15개 있으니 1,000,000,000,000,000 1000 조 번 이상 반복해야한다. 따라서 우리는 memoization 을 사용하여 기존에 구했던 데이터를 그대로 사용할 것이다. 그럼 실행 횟수가 2^n => n 번으로 극적으로 줄어들게 된다.

public class DivideConquer {
	// memo 해시맵 생성
    static Map<Integer, Long> memo = new HashMap<>();

    public static void main(String[] args) {
        int q = 50;
        Long answer = divideConquer(q);
        System.out.println("피보나치 " + q + " 은 " + answer);
    }

    public static Long divideConquer(int x) {
    	// 1 1 2 3 5 ... 형식으로 가기 때문에 최초 앞에 2개는 1 로 설정
        if (x <= 2) return 1L;
        
        // 메모 해시맵에 해당 키가 있다면 해당 값을 반환
        if (memo.containsKey(x)) return memo.get(x);
        
        // 없다면 계산 후 변수에 저장
        long value = divideConquer(x - 1) + divideConquer(x - 2);
        memo.put(x, value);
        return value;
    }
}

예제 1. 2xn 타일링

대표적인 dp의 기본 예제이다.

여기서 가장 중요한 것은 패턴을 찾고 해당 패턴을 점화식으로 만드는 것이다. 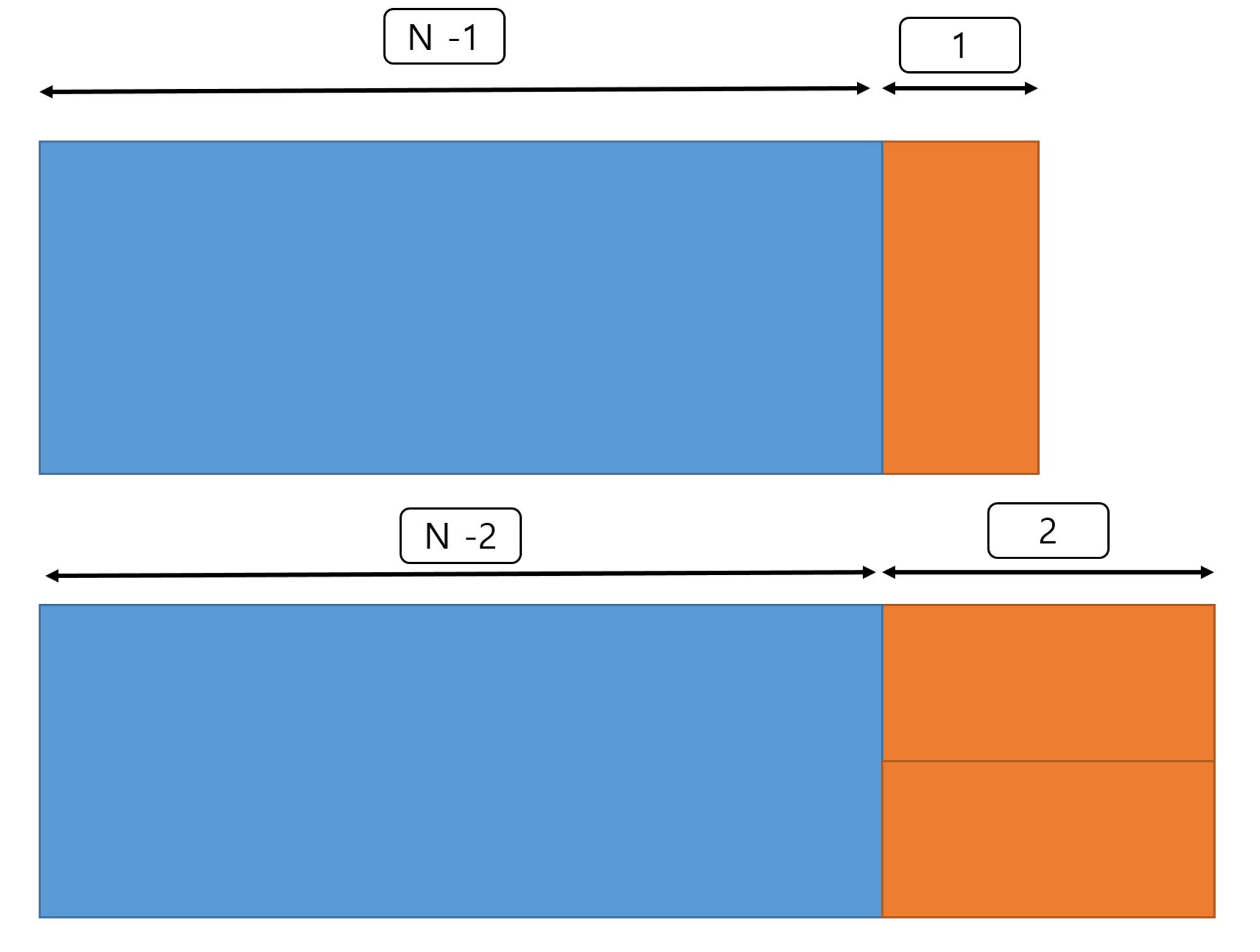위 사진을 보면 한 칸 늘어났을 때의 경우의 수는 1개 이고 두 칸 늘어났을 때 경우의 수 역시 1개 이다. 따라서 N 은 n-1 과 n-2 방법을 더한 것이 바로 N 의 값이 되기 때문에 점화식은 피보나치 수열과 같다. D[i] = D[i-1] + D[i-2]

import java.io.*;
import java.util.HashMap;

public class BackJoon11726 {
    private static HashMap<Long, Long> memo = new HashMap<>();

    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        Long ffibonacchhi = ffibonacchhi(Long.parseLong(br.readLine()));
        System.out.println(ffibonacchhi);
    }

    public static Long ffibonacchhi(Long x) {
        if(x==1) return 1L;
        if(x==2) return 2L;
        if(memo.containsKey(x)) return memo.get(x);
        long value = (ffibonacchhi(x - 1) + ffibonacchhi(x - 2)) % 10007;
        memo.put(x, value);
        return value;
    }
}

예제 2. 2xn 타일링 2

대표적인 dp의 기본 예제의 응용 버전 이다.

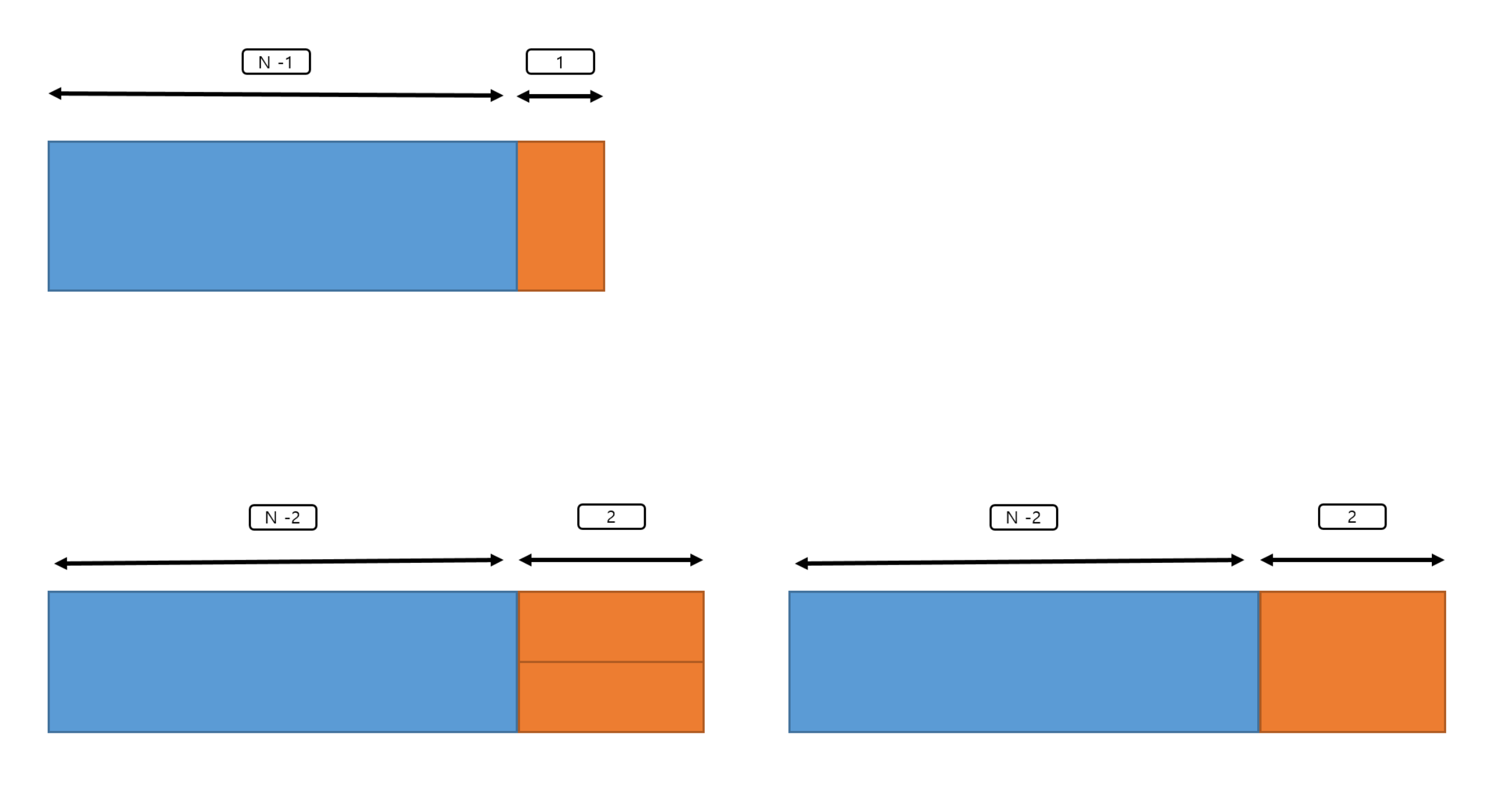
문제에서 추가된 것은 2x2 의 정사각형이 추가되었다. 2칸이 증가되었을 때 방법이 하나 추가된 것이니 방법의 수는 X2 가 된다.
따라서 위 ffibonacchhi 함수의 점화식에서 D[i] = D[i-1] + 2*D[i-2] 로 수정만 해주고, 놓치면 안 되는 부분은 이제 2가 될 경우엔 총 3가지의 방법이 있기 때문에 x 가 2인 경우엔 2L 이 아닌 3L 이 되면 된다.

예제 3. 타일 채우기

이 문제는 한 번 더 꼬아서 생각해야하고 손으로 6번 까지는 그려보고 알았다.

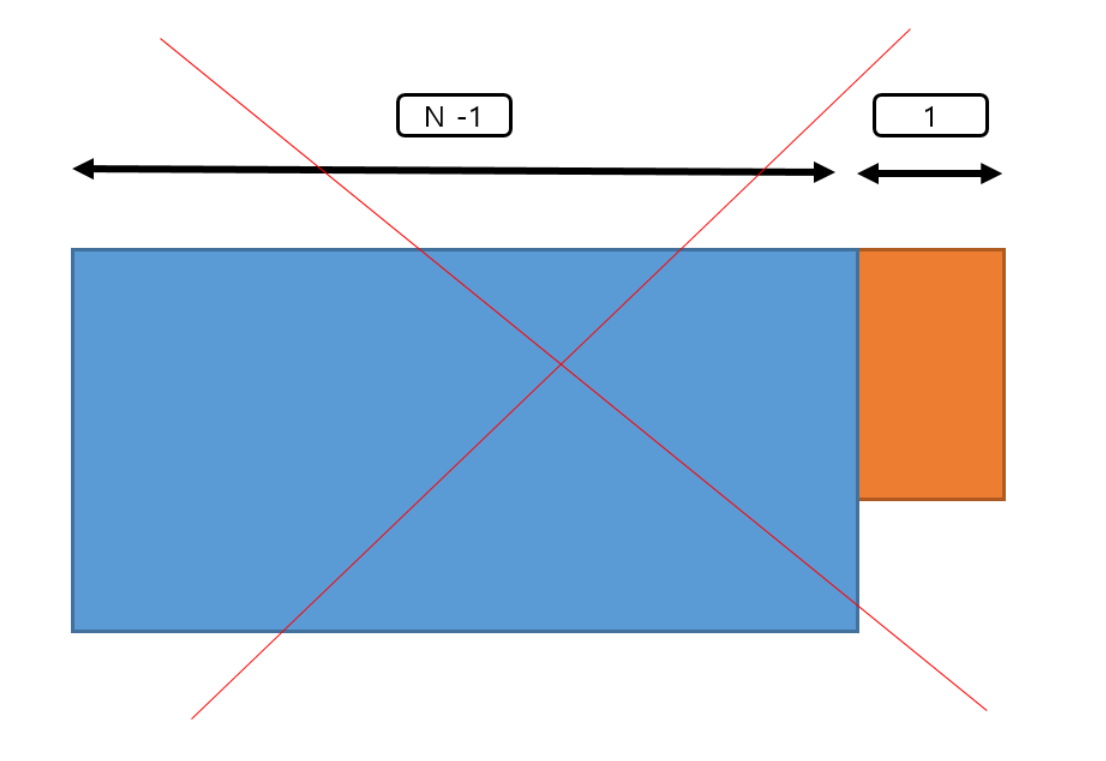
홀수들은 1x2 혹은 2x1 즉, 넓이가 짝수로 늘어나는 방법은 타일을 채울 수 없다. 그러므로 홀수는 제외.
짝수일 경우는
2일 경우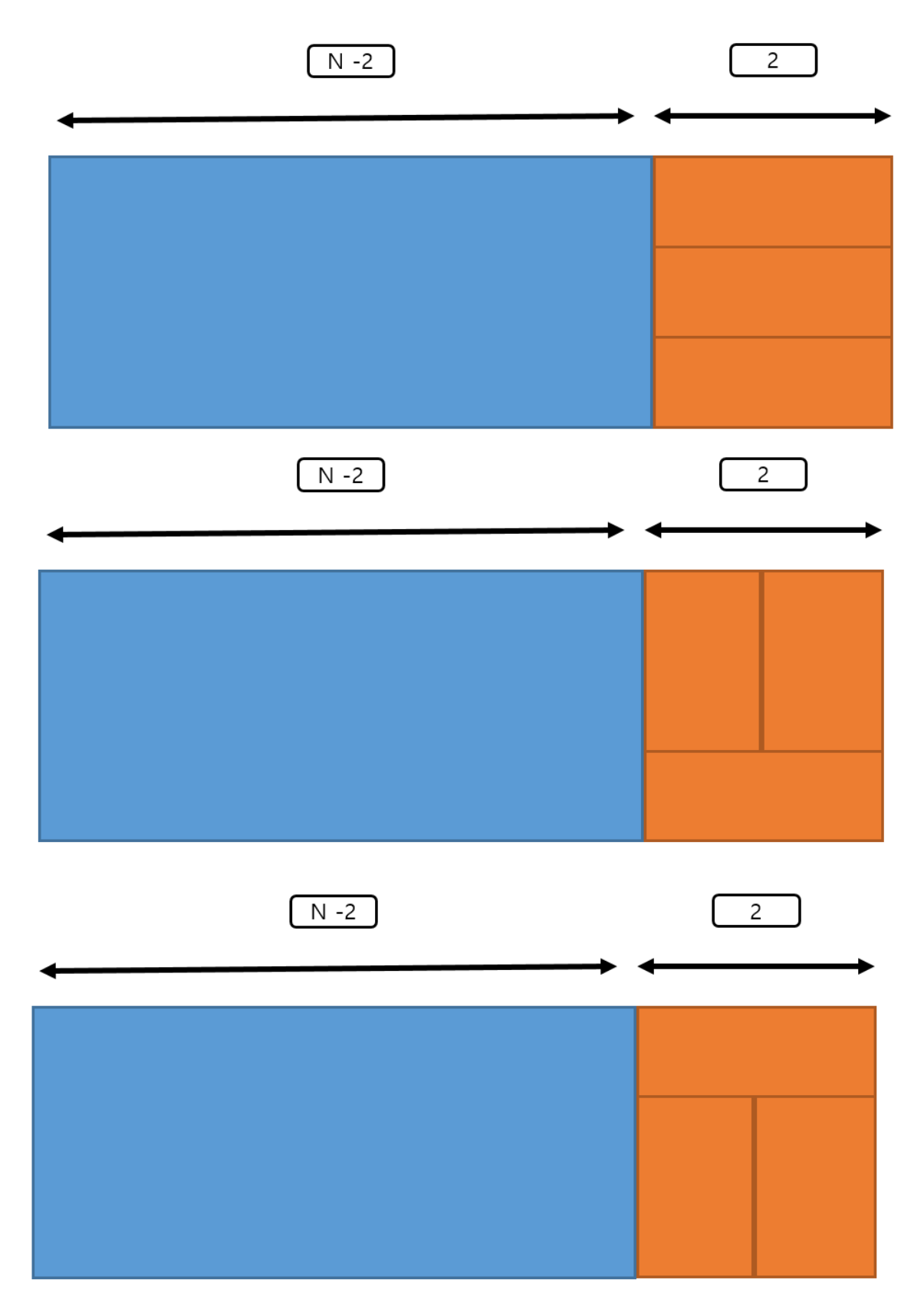

4일 경우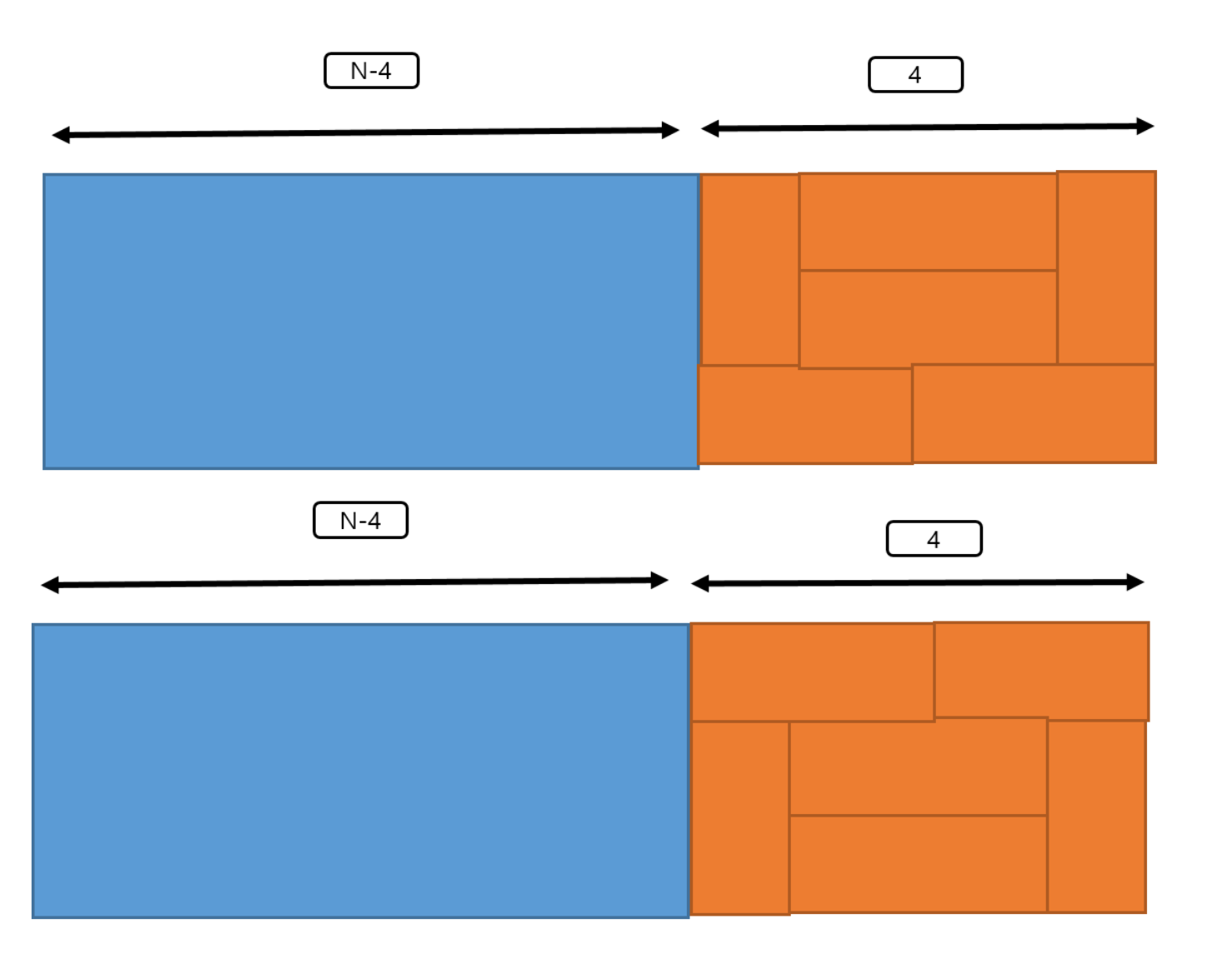

6일 경우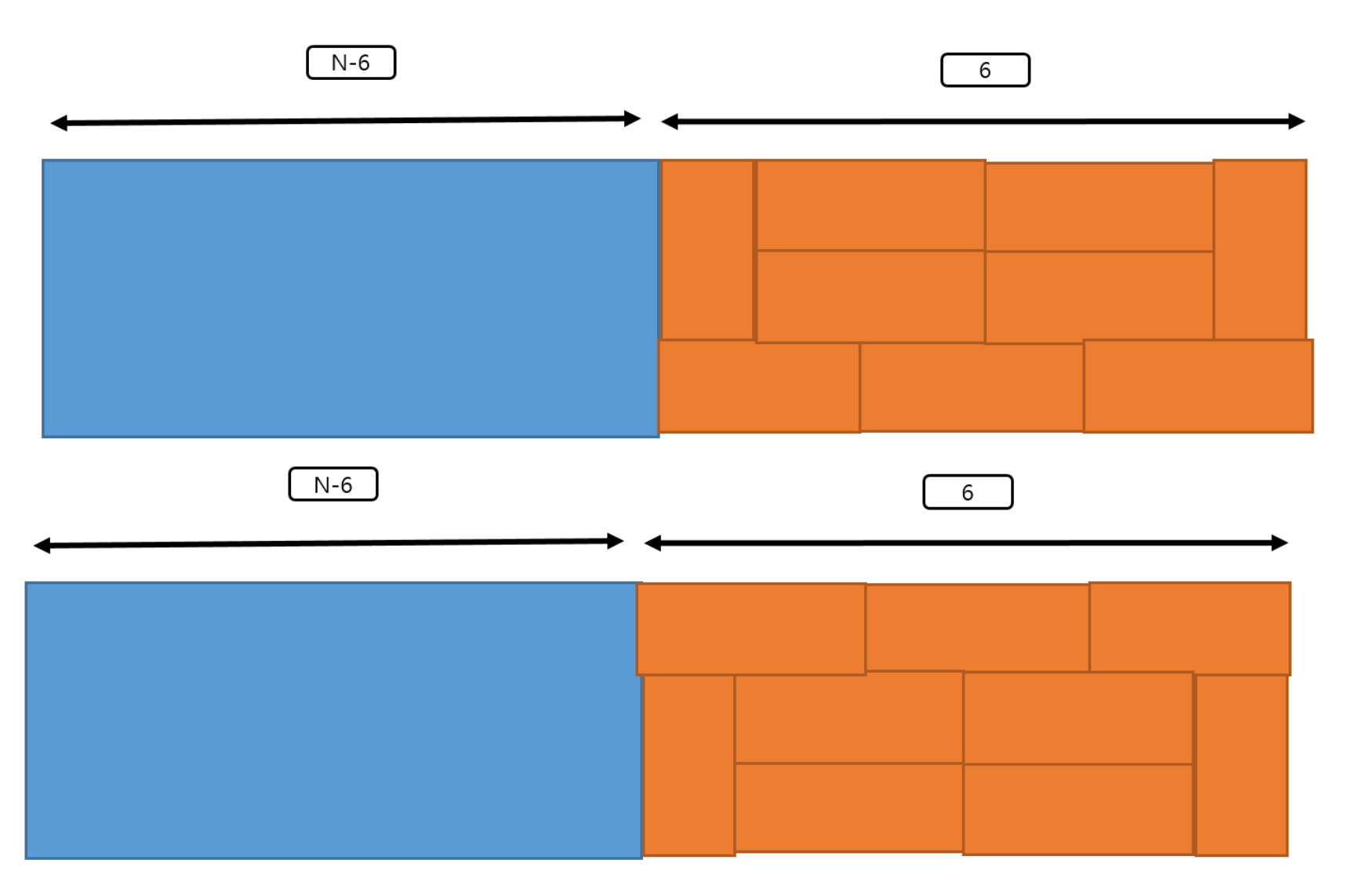

이렇게 n+2 개씩 2개의 경우의 수가 계속 추가되어야한다. 따라서 10 의 점화식을 보면 D[10] = 3*D[8] + 2*D[6] + 2*D[4] + 2*D[2] + 2*D[0] 이 되고 이를 코드으로 옮기면

import java.io.*;
import java.util.*;

public class BackJoon2133 {
    private static Map<Integer, Integer> memo = new HashMap<>();

    public static void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        System.out.println("정답은: "+ffibonachi(N));
    }

    public static int ffibonachi(int x) {
        if(x == 0) return 1;
        // 초기값 2는 3
        if(x == 2) return 3;
        // 홀수는 0
        if(x % 2 != 0) return 0;

        if(memo.containsKey(x)) return memo.get(x);

        // 점화식 계산
        int sum = 3 * ffibonachi(x - 2);
        for (int i = 4; i <= x; i += 2) {
            sum += 2 * ffibonachi(x - i);
        }
        memo.put(x, sum);
        return sum;
    }
}

여기서 n 이 0일 때 왜 1일까? 생각할 수 있을 텐데 앞서 작성한 점화식을 수식으로 옮기면 다음과 같다.

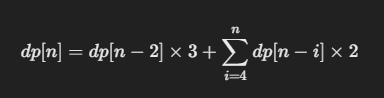
그리고 이때 n 에 2를 집어넣었을 때 가장 기본으로 dp[0] = 1 이 되어야 뒤에 곱하는 값이 0이 안 되기 때문이다.

예제 4. 타일 채우기 3 [2차원 DP]

문제

import java.io.*;
import java.util.*;

public class BackJoon14852 {
    private static Map<Integer, Integer> memo = new HashMap<>();

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        System.out.println(pibonacchi(Integer.parseInt(br.readLine())));
    }

    public static int pibonacchi(int x) {
        if(x==0) return 1;
        if(x==1) return 2;
        if(memo.containsKey(x)) return memo.get(x);
        int sum = 2 * pibonacchi(x - 1);
        sum += 3 * pibonacchi(x - 2);
        for (int i = 3; i <= x; i++) {
            sum += 2 * pibonacchi(x - i);
        }
        memo.put(x, sum);
        return sum % 1_000_000_007;
    }
}

앞서 분 문제와 굉장히 유사하다 그래서 바로 풀었더니 바로 "시간초과" 바로 여기서 앞에서 풀면서 의아했던 점이 바로 풀렸다. D[10] = 3*D[8] + 2*D[6] + 2*D[4] + 2*D[2] + 2*D[0] 앞서 작성했던 이 식을 생각해보면 각각의 D[n-2i] 에 각각의 *2 연산이 계속 들어가고 있다. 그래서 이를 어떻게 하면 좋을까 고민하다 도저히 정답을 모르겠어 해답지를 보니

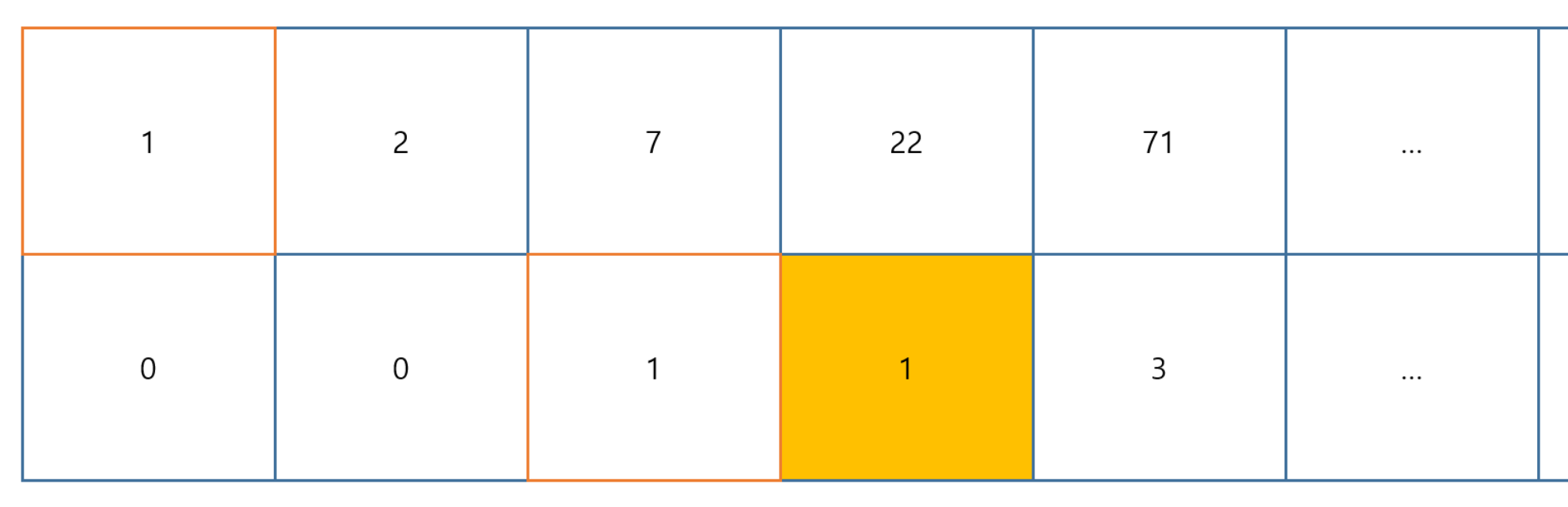
이렇게 2차원 dp 를 사용하여 패턴을 찾아내면 된다. 그럼 위에서 작성 예제대로 D[10] 를 구해보자.
1. dp[i][0] 은 앞서 우리가 구한 일반 점화식을 계산한 값이 들어간다고 생각한다. 3*D[8] + 2*D[6]
2. dp[i][1] 은 일반 점화식 이외에 추가적으로 계산되는 값이 들어간다. 2*D[4] + 2*D[2] + 2*D[0]
3. dp[i][1] 은 바로 한 칸 앞 dp[i-1][1] 와 2칸 앞의 dp[i-3][0] 을 넣어주면 된다.

import java.io.*;

public class BackJoon14852 {
    private static final int MOD = 1_000_000_007;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());

        int [][] memo = new int[N + 1][N + 1];

        System.out.println(pibonacchi(memo, N));
    }

    public static int pibonacchi(int[][] memo, int x) {
        // 2차원 memo 테이블 생성
        memo[0][0] = 1;
        memo[1][0] = 2;
        memo[2][0] = 7;
        memo[0][1] = 0;
        memo[1][1] = 0;
        memo[2][1] = 1;

        // 점화식
        for (int i = 3; i <= x; i++) {
            memo[i][1] = (memo[i - 3][0] + memo[i - 1][1]) % MOD;
            memo[i][0] = (2 * memo[i - 1][0] + 3 * memo[i - 2][0] + 2 * memo[i][1]) % MOD;
        }

        return memo[x][0];
    }
}

• 위 코드에서 2차원 dp 를 memo 라고 작성하였으나 dp 라고 작성하는 것이 변수명 짖는 규칙에 맞아보입니다.

import java.io.*;

public class BackJoon14852 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        System.out.println(solve(N));
    }

    public static int solve(int N) {
        final int MOD = 1_000_000_007;

        if (N == 0) return 1;
        if (N == 1) return 2;
        if (N == 2) return 7;

        // DP 배열 선언
        int[] dp = new int[N + 1];
        int[] sum = new int[N + 1]; // 누적합 배열

        // 초기값 설정
        dp[0] = 1;
        dp[1] = 2;
        dp[2] = 7;

        sum[0] = dp[0];
        sum[1] = (sum[0] + dp[1]) % MOD;
        sum[2] = (sum[1] + dp[2]) % MOD;

        // 점화식 계산
        for (int i = 3; i <= N; i++) {
            dp[i] = (2 * dp[i - 1] + 3 * dp[i - 2] + 2 * sum[i - 3]) % MOD;
            sum[i] = (sum[i - 1] + dp[i]) % MOD;
        }

        return dp[N];
    }
}