탐색
너비 우선 탐색
📝 정의
탐색을 할 때 너비를 우선으로 하여 탐색을 수행하는 탐색 알고리즘이다.
"특히 맹목적인 탐색"을 하고자 할 때 사용할 수 있는 탐색 기법이다.
🛠 특징
너비 우선 탐색은 '최단 경로'를 찾아준다는 점에서 최단 길이를 보장해야할 때 많이 사용한다.
너비 우선 탐색은 Queue 로 구현한다.
⚙ 동작
- 큐에서 하나의 노드를 꺼낸다.
- 해당 노드에 연결된 노드 중 방문하지 않은 노드를 방문하고, 차례대로 큐에 삽입한다.
- 1-2 를 반복한다.
public class BFS {
public static void main(String[] args) {
ArrayList<List<Integer>> graph = new ArrayList<>();
int numOfNodes = 6;
for (int i = 0; i <= numOfNodes; i++) {
graph.add(new ArrayList<>());
}
// 간선은 양 방향 연결이어야 함.
graph.get(1).add(2);
graph.get(2).add(1);
graph.get(1).add(3);
graph.get(3).add(1);
graph.get(2).add(4);
graph.get(4).add(2);
graph.get(2).add(5);
graph.get(5).add(2);
graph.get(3).add(6);
graph.get(6).add(3);
bfs(1, graph, numOfNodes);
}
public static void bfs(int start, ArrayList<List<Integer>> graph, int numOfNodes) {
Queue<Integer> q = new LinkedList<>();
boolean[] visited = new boolean[numOfNodes + 1];
q.add(start);
visited[start] = true;
while (!q.isEmpty()) {
int current = q.poll();
System.out.print(current + " ");
for (Integer neighbor : graph.get(current)) {
if (!visited[neighbor]) {
q.add(neighbor);
visited[neighbor] = true;
}
}
}
}
}깊이 우선 탐색
📝 정의
탐색을 할 때 깊이를 우선으로 하여 탐색을 수행하는 탐색 알고리즘이다.
"특히 맹목적인 탐색"을 하고자 할 때 사용할 수 있는 탐색 기법이다.
🛠 특징
너비 우선 탐색은 Stack 로 구현한다.
그런데 Stack 을 사용하지 않고 재귀만 사용해서도 구현이 가능하다.
⚙ 동작
- 큐에서 하나의 노드를 꺼낸다.
- 해당 노드에 연결된 노드 중 방문하지 않은 노드를 방문하고, 차례대로 큐에 삽입한다.
- 1-2 를 반복한다.
public class DFS {
public static void main(String[] args) {
List<List<Integer>> graph = new ArrayList<>();
int numOfNodes = 6; // 노드 수
for (int i = 0; i <= numOfNodes; i++) {
graph.add(new ArrayList<>());
}
// 간선 추가 (양방향 그래프 예시)
graph.get(1).add(2);
graph.get(1).add(3);
graph.get(2).add(4);
graph.get(2).add(5);
graph.get(3).add(6);
// 양방향 추가 (반대 방향도 추가)
graph.get(2).add(1);
graph.get(3).add(1);
graph.get(4).add(2);
graph.get(5).add(2);
graph.get(6).add(3);
boolean[] visited = new boolean[numOfNodes + 1];
dfs(1, graph, visited);
}
public static void dfs(int node, List<List<Integer>> graph, boolean[] visited) {
visited[node] = true;
System.out.print(node + " ");
for (int neighbor : graph.get(node)) {
if (!visited[neighbor]) {
dfs(neighbor, graph, visited);
}
}
}
}합집합 찾기
📝 정의
대표적인 그래프 알고리즘이다.
서로소 집합 ( Disjoint-set ) 알고리즘이라고도 불린다. 즉, 합집합 알고리즘은 서로 같은 집합이 아닌 것들을 찾는 것과 같다고도 볼 수 있다.
여러 개의 노드가 존재할 때 두개의 노드를 선택해서, 현재 이 두 노드가 서로 같은 그래프에 속하는 판별하는 알고리즘
🛠 특징
크루스칼 알고리즘의 밑걸음이 된다.
2개의 노드를 합치고 더 작은 값을 "부모" 로 칭하는데 이를 "유니온" 이라고 하고, 최종 부모 노드를 찾아가는 것을 재귀로 구현한다.
⚙ 동작
- 최초에 이렇게 무질서 하게 노드가 존재한다고 가정한다. 이는 각각의 노드의 부모가 자기 자신이 되는 것이다.
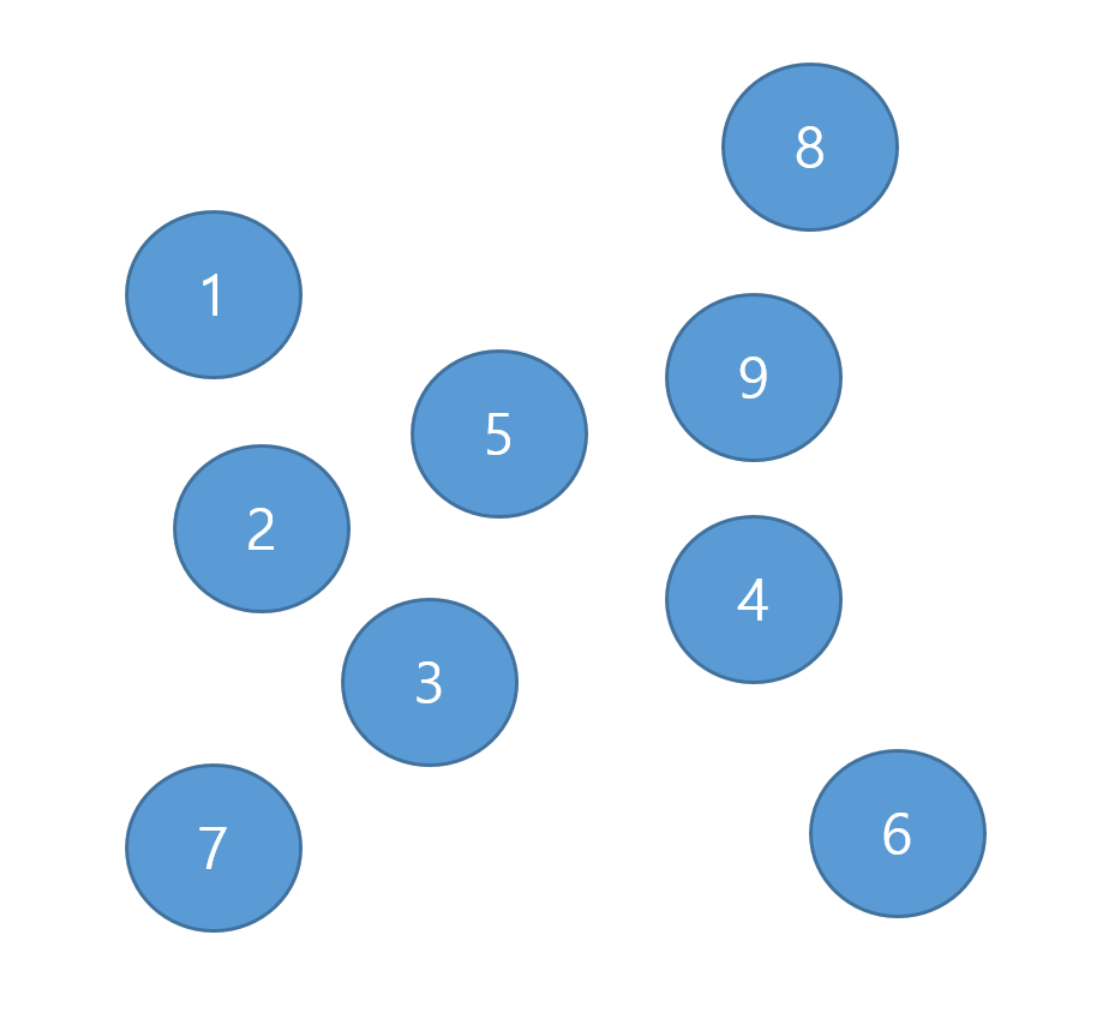
| 자식 | 1 | 2 | 3 | 4 | ... | 9 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 2 | 3 | 4 | ... | 9 |
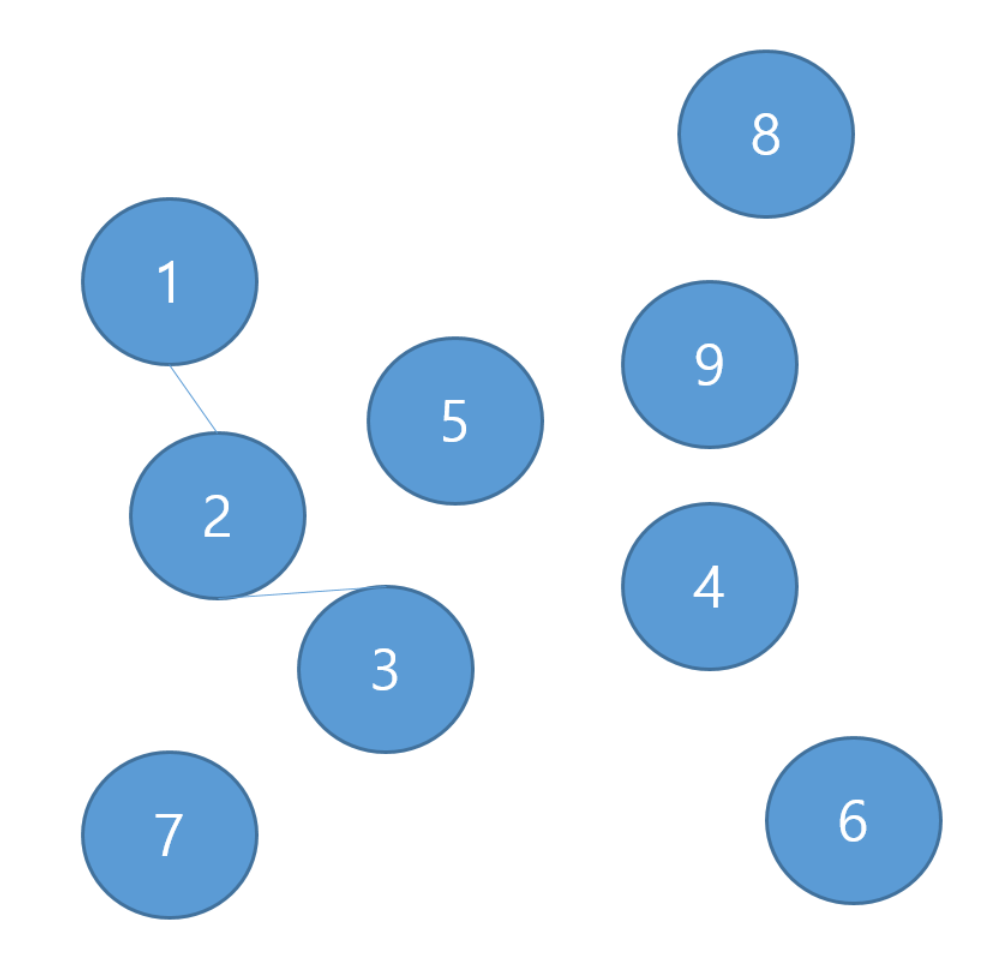
| 자식 | 1 | 2 | 3 | 4 | ... | 9 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 1 | 2 | 4 | ... | 9 |
이렇게 간선이 생성될 때 간선에 붙은 2개의 노드 중 더 작은 노드쪽으로 값을 합친다. 이것이 바로 합침(Union) 이라 하는 것이다.
- 그리고 여기서 1과 3이 연결되었는지 는 부모노드만 보고는 판별할 수 없기 때문에 여기서 재귀가 사용된다.
그래서 결과적으로 Union 연산이 다 수행되고 나면 아래와 같이 된다.
| 자식 | 1 | 2 | 3 | 4 | ... | 9 |
|---|---|---|---|---|---|---|
| 부모 | 1 | 1 | 1 | 4 | ... | 9 |
public class Union {
public static void main(String[] args) {
int[] ary = new int[11];
for (int i = 0; i <= 10; i++) {
ary[i] = i;
}
// 위 사진과 같은 간선을 생성하기
unionParent(ary, 1, 2);
unionParent(ary, 2, 3);
unionParent(ary, 3, 4);
unionParent(ary, 4, 5);
unionParent(ary, 6, 7);
unionParent(ary, 7, 8);
unionParent(ary, 8, 9);
unionParent(ary, 9, 10);
// 여기에 1, 9 든 2, 8 이든 서로 간섭하지 않던 두 집합을 하나의 간선으로 연결 해준 후
// findParent 를 하면 결과가 다르게 나올 것이다.
findParent(ary, 1, 10);
}
public static int getParent(int[] parent, int x) {
if(parent[x]==x) return x;
return parent[x] = getParent(parent, parent[x]);
}
public static void unionParent(int[] parent, int x, int y) {
x = getParent(parent, x);
y = getParent(parent, y);
if (x > y) {
parent[x] = y;
} else {
parent[y] = x;
}
}
public static void findParent(int[] parent, int x, int y) {
x = getParent(parent, x);
y = getParent(parent, y);
if (x == y) {
System.out.println("부모가 동일합니다.");
} else {
System.out.println("부모가 다릅니다.");
}
}
}
크루스칼 알고리즘
📝 정의
가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘이다.
즉, 최소비용 신장트리를 만들기 위한 대표적인 알고리즘이다.
예를들어 여러 개의 도시가 있을 때 각 도시를 도로를 이용해 연결하고자 할 때 비용을 최소한으로 하고자 할 때 적용하는 알고리즘이다.
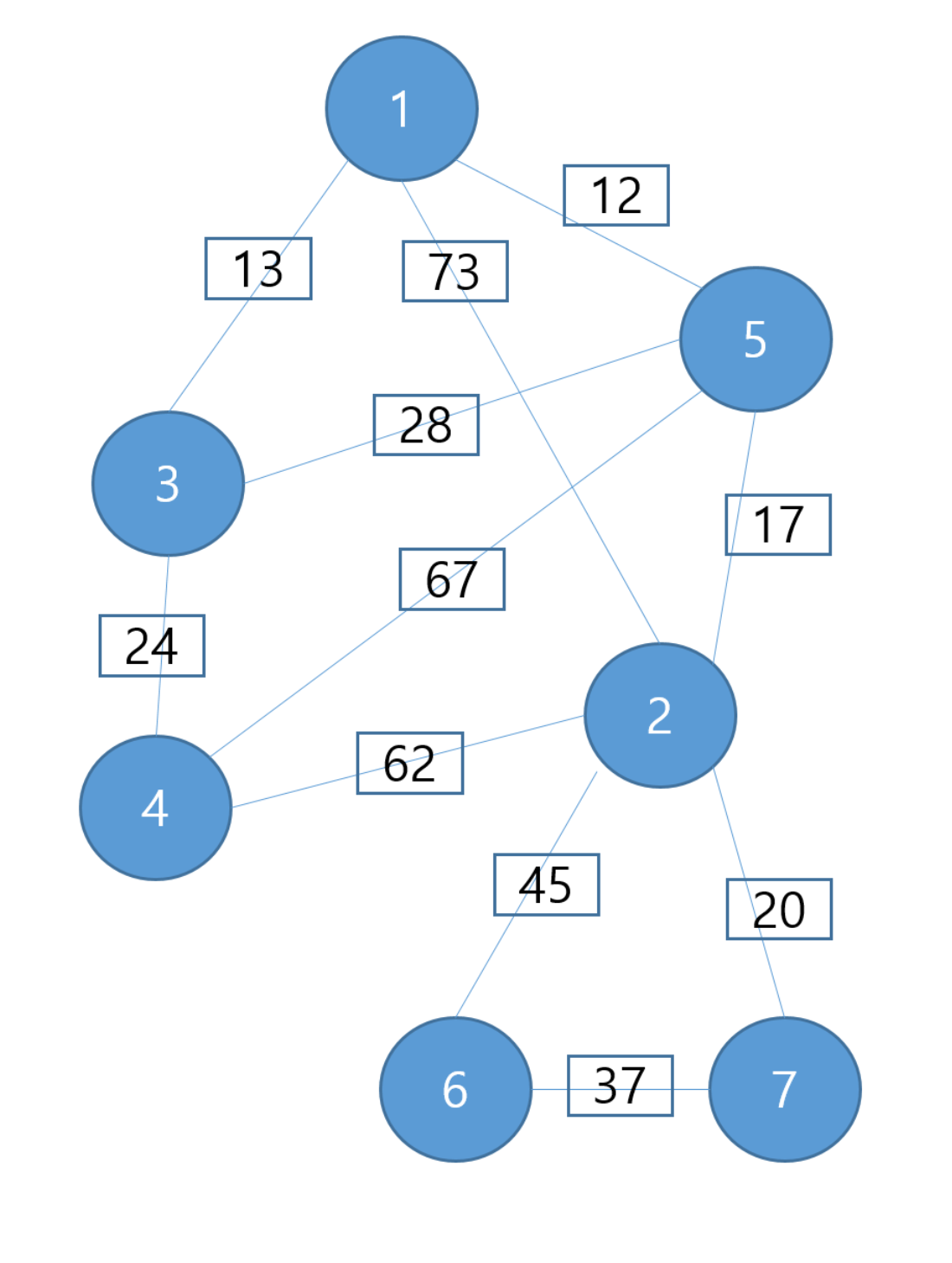
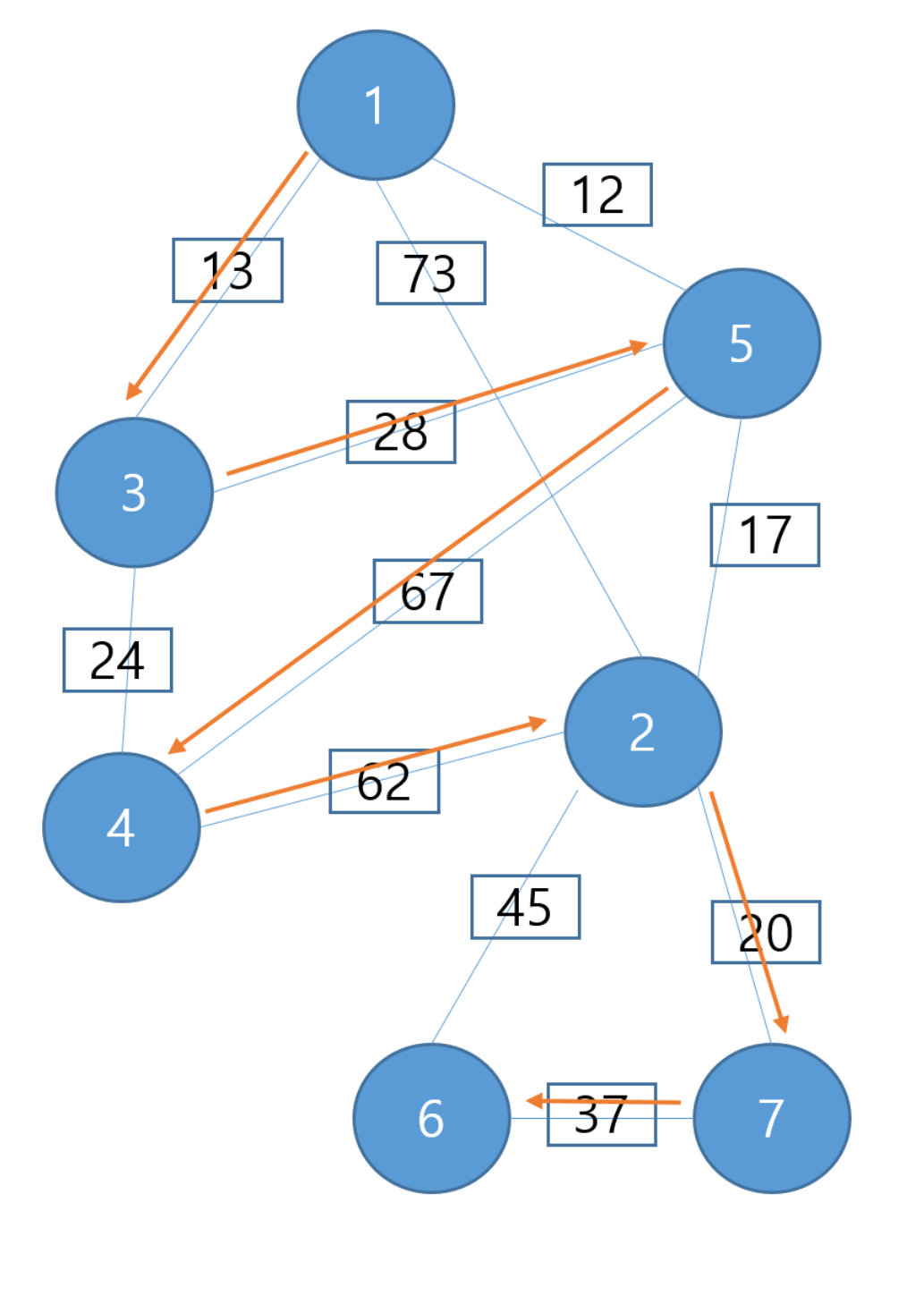
이렇게 최소한의 비용을 사용하여 모든 노드를 연결하는 방법을 찾는 알고리즘이다.
🛠 특징
크루스칼 알고리즘에서 모든 노드를 연결할 때 최소 비용은 반드시 노드-1 개의 간선을 사용하는 것이다.
방법은 간선을 거리가 짧은 순서대로 그래프에 포함시킨다.
여기서 사이클을 형성하면 안 된다.
사이클이란?
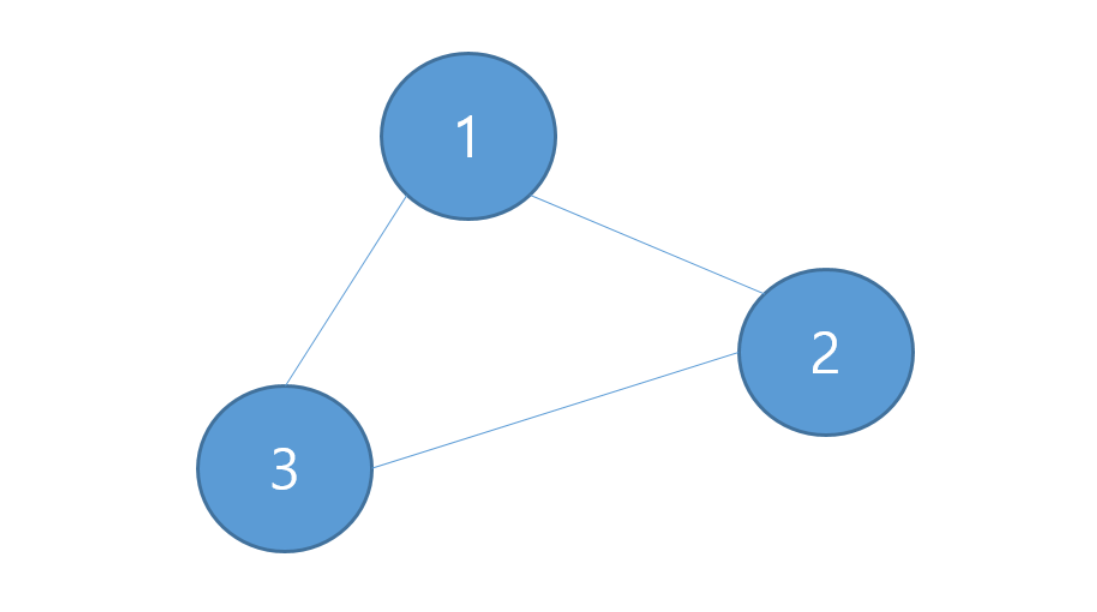
이렇게 폐회로가 형성되는 경우를 사이클이라 한다.
⚙ 동작
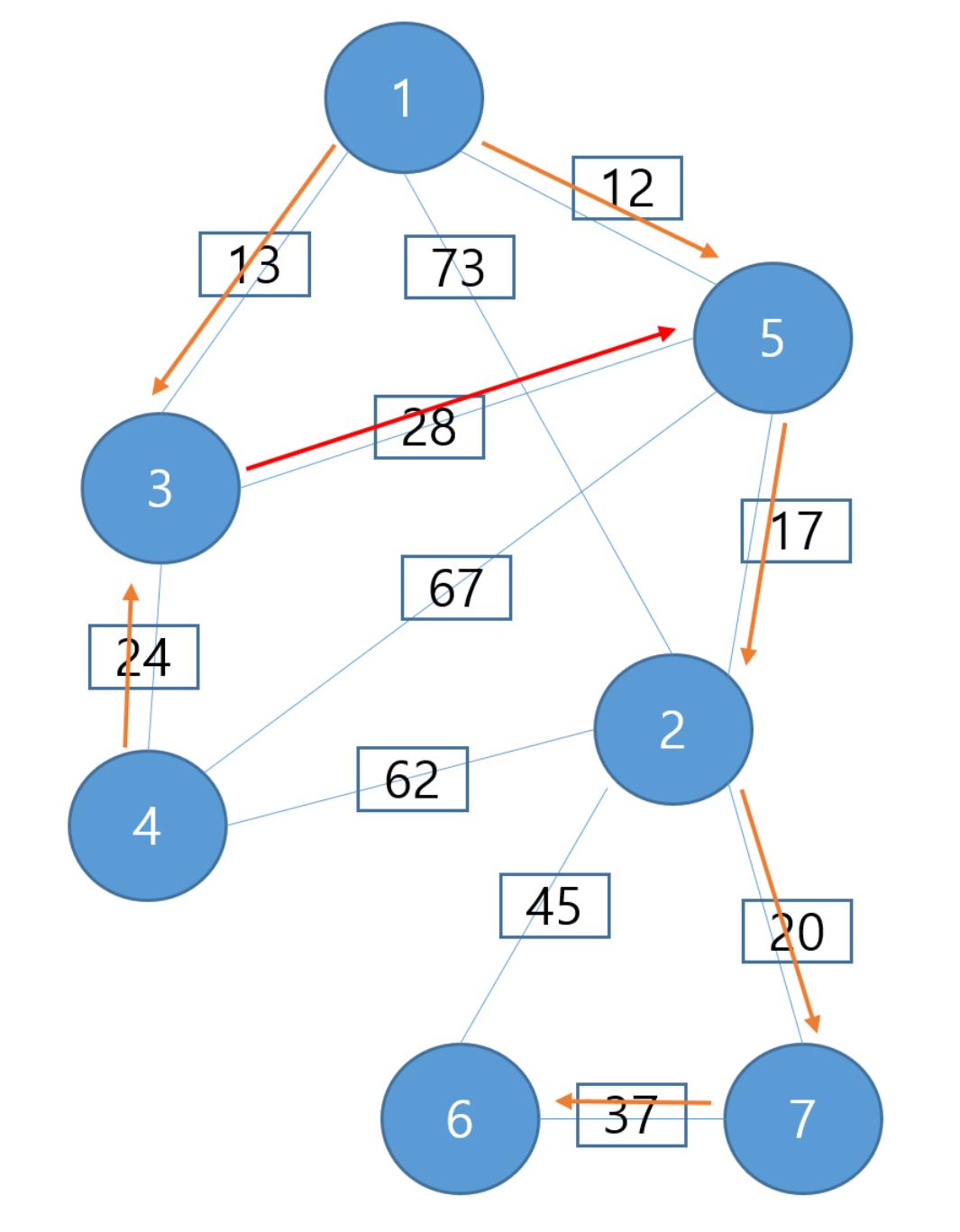
- 모든 간선들을 거리를 기준으로 먼저 오름차순 정렬을 수행
- 정렬된 순서에 맞게 그래프에 포함
- 포함하기 전 사이클 테이블을 확인
- 사이클을 형성하는 경우 간선을 포함 X
위 일련의 동작 과정을 통해 7개의 노드에 6개의 간선을 그려넣었다.
우선 12, 13, 17, 20, 24 를 그래프에 포함시키고 다음 28 인데 28을 넣으면 사이클 테이블에 들어가기 때문에 제외
다음 37을 포함시킴으로써 드디어 모든 노드가 연결이 되었다.
그럼 여기서 어떻게 Union 알고리즘을 접목하여 사용할 수 있을까? => 바로 사이클 테이블을 구성할 때 사용한다.
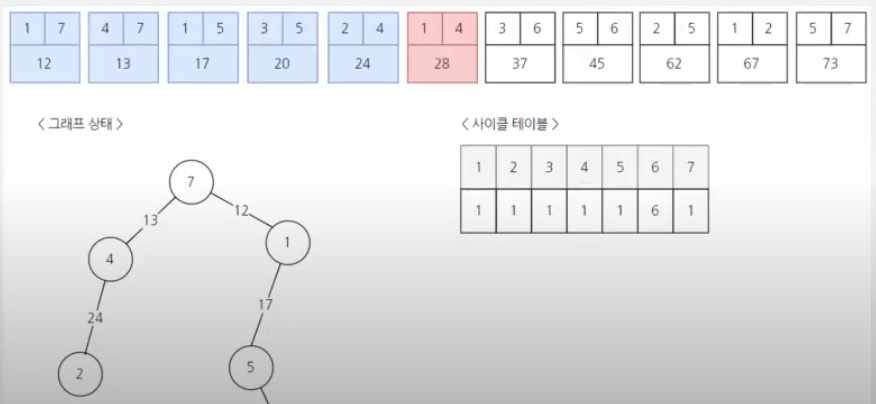여기 위 사진에서 사이클 테이블에 간선 기준으로 정렬하고 해당 간선에 연결된 노드 2개가 사이클 테이블에 모두 같은 부모를 가르키고 있으면 사이클이 형성되기 때문에 제끼고 넘어가면 된다.
public class Kruskal {
static class Edge implements Comparable<Edge> {
int from, to, weight;
Edge(int from, int to, int weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public int compareTo(Edge o) {
return this.weight - o.weight;
}
}
static class UnionFind {
private int[] parent, rank;
// union 사이클 테이블 생성
UnionFind(int size) {
parent = new int[size + 1];
rank = new int[size + 1];
for (int i = 0; i <= size; i++) {
parent[i] = i;
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
// union 사이클 테이블에 사이클이 발생하는지 bool 값으로 반환하는 함수
public boolean union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX == rootY) {
return false;
}
if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else {
parent[rootY] = rootX;
rank[rootX]++;
}
return true;
}
}
public static void main(String[] args) {
List<Edge> edges = new ArrayList<>();
edges.add(new Edge(1, 7, 12));
edges.add(new Edge(1, 4, 28));
edges.add(new Edge(1, 2, 67));
edges.add(new Edge(1, 5, 17));
edges.add(new Edge(2, 4, 24));
edges.add(new Edge(2, 5, 62));
edges.add(new Edge(3, 5, 20));
edges.add(new Edge(3, 6, 37));
edges.add(new Edge(4, 7, 13));
edges.add(new Edge(5, 6, 45));
edges.add(new Edge(5, 7, 73));
int numOfNodes = 7;
kruskal(numOfNodes, edges);
}
public static void kruskal(int numOfNodes, List<Edge> edges) {
Collections.sort(edges);
UnionFind uf = new UnionFind(numOfNodes);
// 모든 노드를 연결한 간선의 최종 길이
int mstWeight = 0;
// 크루스칼 알고리즘을 통해 최종적으로 들어갈 배열 생성
List<Edge> mst = new ArrayList<>();
// 모든 노드를 돌며
for (Edge edge : edges) {
// 사이클이 발생하지 않으면 최종 answer 에 추가
if (uf.union(edge.from, edge.to)) {
mst.add(edge);
mstWeight += edge.weight;
}
}
System.out.println("최소 신장 트리의 총 가중치: " + mstWeight);
for (Edge edge : mst) {
System.out.println(edge.from + " - " + edge.to + " (가중치: " + edge.weight + ")");
}
}
}
# 최소 신장 트리의 총 가중치: 123
# 1 - 7 (가중치: 12)
# 4 - 7 (가중치: 13)
# 1 - 5 (가중치: 17)
# 3 - 5 (가중치: 20)
# 2 - 4 (가중치: 24)
# 3 - 6 (가중치: 37)
이진 트리의 구현과 순회(Traversal) 방식
📝 정의
기본적으로 가장 많이 사용되는 비선형 자료구조는 Binary Tree 이다.
이진 트리는 트리 자료구조를 활용한 대표적인 예시로 데이터의 탐색 속도 증진을 위해 사용하는 구조이다.
🛠 특징
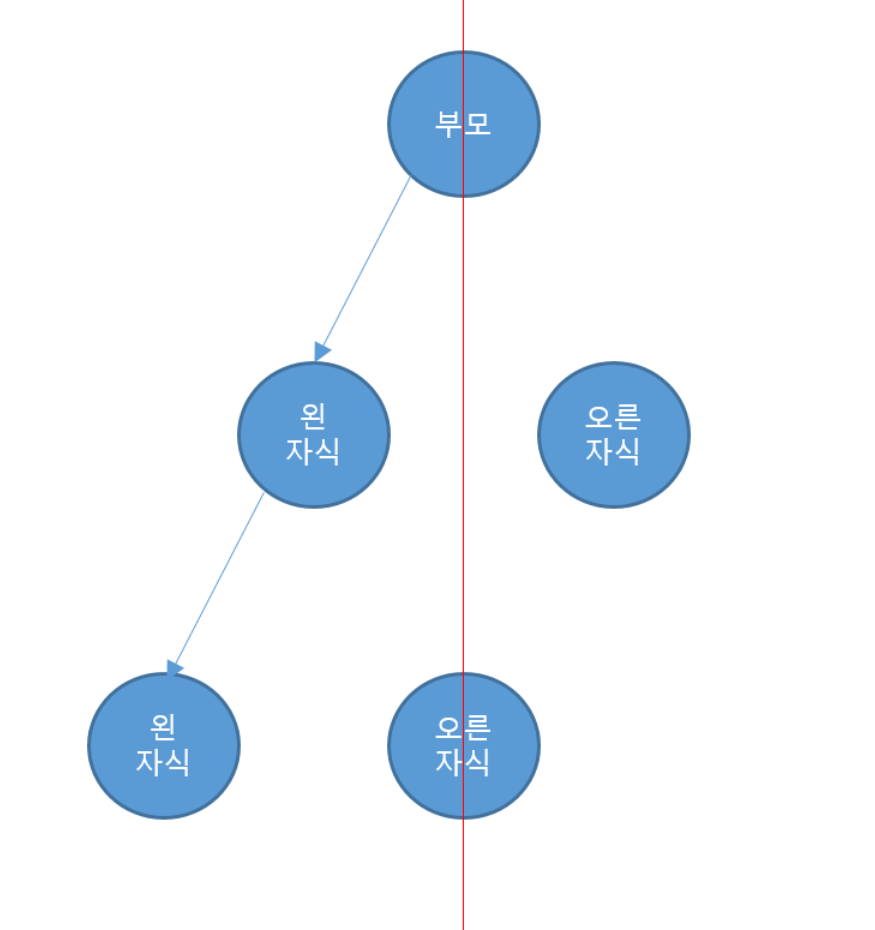한 간선을 내려갈 때마다 반대쪽 방향의 노드는 볼 필요가 없기 때문에 1/2 씩 줄어들게 된다. 이는 높이: log2n 을 갖는다. 그렇기 때문에 탐색 속도가 매우 빠르다고 할 수 있다.
그런데 이 이진 트리에서 "포인터"의 개념이 들어오는데 힙 정렬을 구현할 때는 완전 이진 트리가 사용되었다.
반면 그냥 이진 트리는 배열로 표현하기 어렵다. 왜냐하면 완전 정렬이 안 되어있을 수 있기 때문이다. 그리고 이를 코드적으로 설명하자면
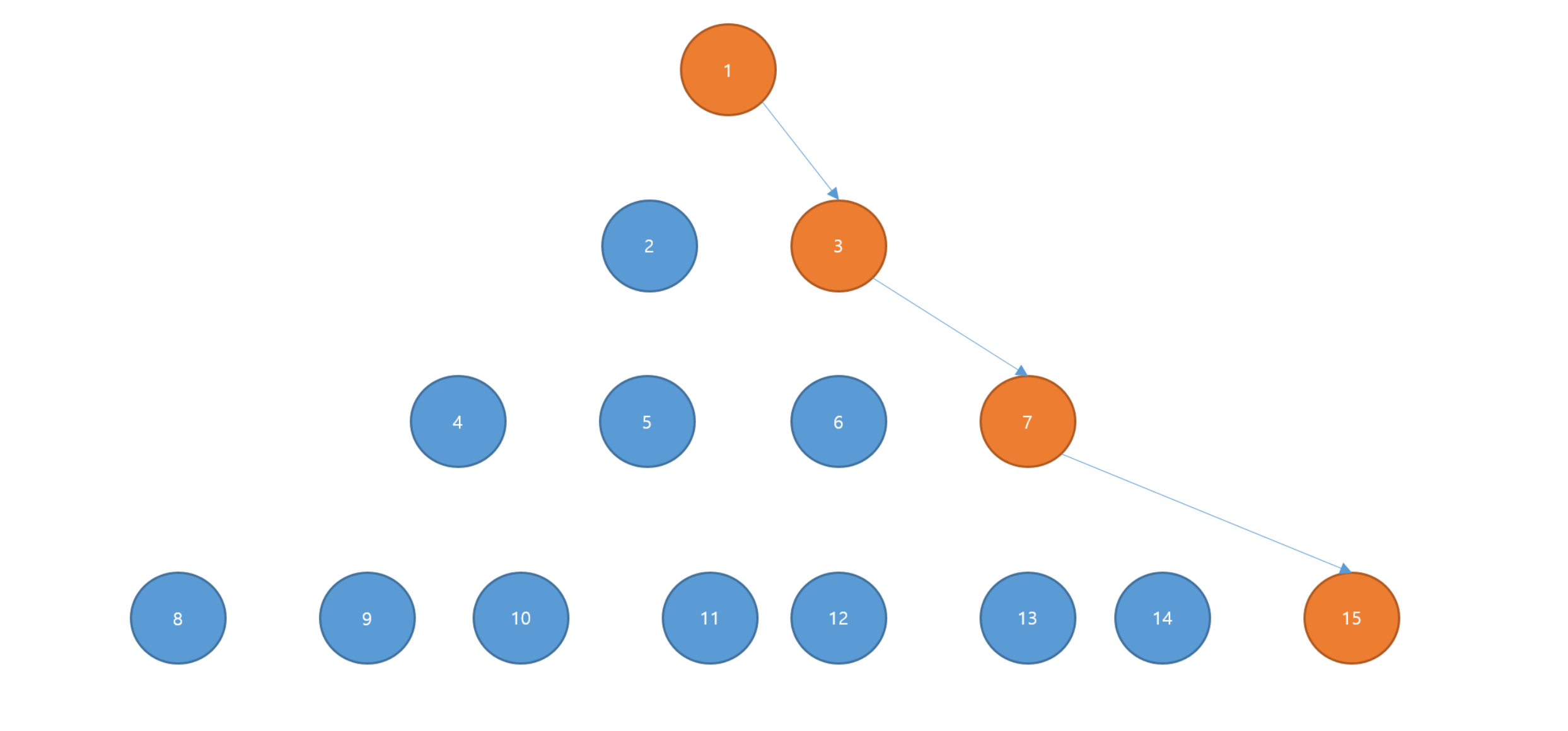단순히 4 개의 이진 트리를 표현하고 싶지만 필요한 공간은 15개가 필요하기 때문에 메모리 낭비가 너무 심하다. 따라서 일반 이진 트리는 배열로 표현하기 어렵다.
따라서 "포인터"가 필요한 것이다. 위처럼 4개의 이진 트리를 표현하기 위해서 4개의 공간만 사용하면 되기 때문이다.
-
이진 트리
부모 노드 밑에 2개 이하의 자식 노드만 갖고 있다면 된다. -
완전 이진 트리
heapify 가 완료되어 정렬이 된 상태의 이진트리 -
포화 이진 트리
heapify 가 완료되어 정렬이 완료됨 + 모든 부모 노드는 반드시 2개의 자식 노드를 갖고있어야함.
⚙ 동작
하나의 노드를 방문 했을 때
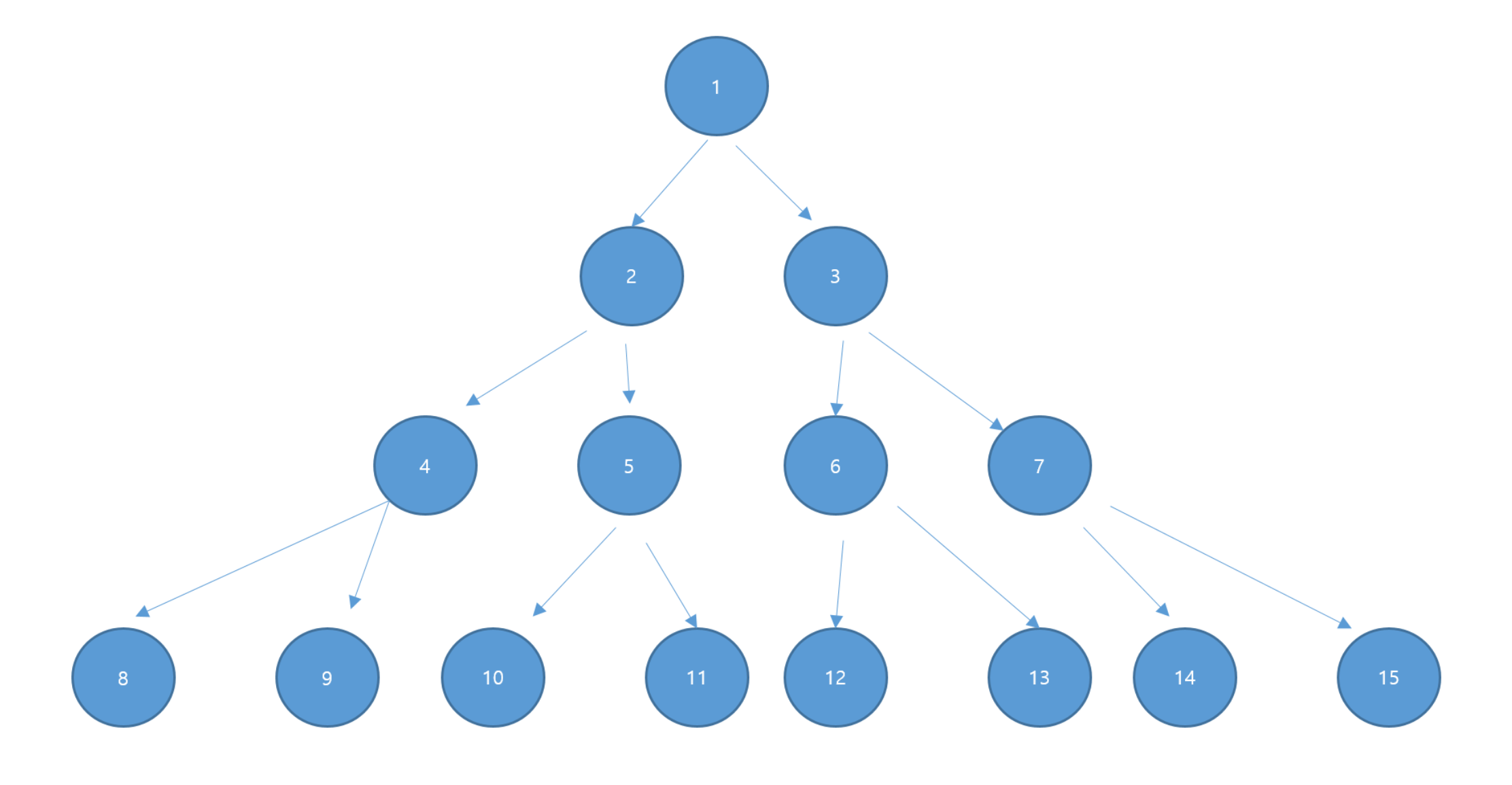
1. 전위 순회 (Preorder Traversal)
- 먼저 자기 자신을 처리
- 왼쪽 자식 방문
- 오른쪽 자식 방문
1 - 2 - 4 - 8 - 9 - 5 - 10 - 11 - 3 - 6- 12 - 13 - 7 - 14 - 15
2. 중위 순회 (Inorder Traversal)
- 왼쪽 자식 방문
- 먼저 자기 자신을 처리
- 오른쪽 자식 방문
8 - 4 - 9 - 2 - 10 - 5 - 11 - 1 - 12 - 6 - 13 - 3 - 14 - 7 - 15
3. 후위 순회 (Postorder Traversal)
- 왼쪽 자식 방문
- 오른쪽 자식 방문
- 먼저 자기 자신을 처리
주로 계산기 수식을 컴퓨터가 이해하기 좋게 후위 순회로 처리함.
8 - 9 - 4 - 10 - 11 - 5 - 2 - 12 - 13 - 6 - 14 - 15 - 7 - 3 - 1
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinaryTree {
Node root;
public BinaryTree() {
this.root = null;
}
// 트리에 새 값을 삽입하는 메서드 (간단한 수동 삽입)
public void insert(int value) {
root = insertRec(root, value);
}
// 재귀적으로 삽입
private Node insertRec(Node current, int value) {
if (current == null) {
return new Node(value);
}
if (value < current.value) {
current.left = insertRec(current.left, value);
} else if (value > current.value) {
current.right = insertRec(current.right, value);
}
return current;
}
// 전위 순회 (루트, 왼쪽, 오른쪽)
public void preorderTraversal(Node node) {
if (node != null) {
System.out.print(node.value + " ");
preorderTraversal(node.left);
preorderTraversal(node.right);
}
}
// 중위 순회 (왼쪽, 루트, 오른쪽)
public void inorderTraversal(Node node) {
if (node != null) {
inorderTraversal(node.left);
System.out.print(node.value + " ");
inorderTraversal(node.right);
}
}
// 후위 순회 (왼쪽, 오른쪽, 루트)
public void postorderTraversal(Node node) {
if (node != null) {
postorderTraversal(node.left);
postorderTraversal(node.right);
System.out.print(node.value + " ");
}
}
// 루트에서 순회를 시작하는 공용 메서드
public void traverseTree(String order) {
System.out.println(order + " traversal:");
switch (order.toLowerCase()) {
case "preorder":
preorderTraversal(root);
break;
case "inorder":
inorderTraversal(root);
break;
case "postorder":
postorderTraversal(root);
break;
default:
System.out.println("Invalid traversal type");
break;
}
System.out.println();
}
// 여기서부터 간단한 이진 트리 예제
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
// 트리에 노드 삽입 (수동)
tree.insert(50);
tree.insert(30);
tree.insert(70);
tree.insert(20);
tree.insert(40);
tree.insert(60);
tree.insert(80);
// 트리 순회
tree.traverseTree("preorder");
tree.traverseTree("inorder");
tree.traverseTree("postorder");
// 완전 이진 트리 예제 (gpt)
CompleteBinaryTree completeTree = new CompleteBinaryTree();
for (int i = 1; i <= 15; i++) {
completeTree.insert(i);
}
System.out.println("Complete Binary Tree - Level Order Traversal:");
completeTree.levelOrderTraversal();
// 균형 이진 탐색 트리 예제 (gpt)
BalancedBinaryTree balancedTree = new BalancedBinaryTree();
balancedTree.buildFromSortedArray(new int[]{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15});
System.out.println("Balanced Binary Tree - Inorder Traversal:");
balancedTree.inorderTraversal(balancedTree.root);
}
}
// 완전 이진 트리 구현 (gpt)
class CompleteBinaryTree {
Node root;
java.util.Queue<Node> queue;
public CompleteBinaryTree() {
this.root = null;
this.queue = new java.util.LinkedList<>();
}
public void insert(int value) {
Node newNode = new Node(value);
if (root == null) {
root = newNode;
queue.add(root);
} else {
Node current = queue.peek();
if (current.left == null) {
current.left = newNode;
} else if (current.right == null) {
current.right = newNode;
queue.poll();
}
queue.add(newNode);
}
}
public void levelOrderTraversal() {
java.util.Queue<Node> tempQueue = new java.util.LinkedList<>();
tempQueue.add(root);
while (!tempQueue.isEmpty()) {
Node current = tempQueue.poll();
System.out.print(current.value + " ");
if (current.left != null) tempQueue.add(current.left);
if (current.right != null) tempQueue.add(current.right);
}
System.out.println();
}
}
// 균형 이진 탐색 트리 구현 (gpt)
class BalancedBinaryTree {
Node root;
public void buildFromSortedArray(int[] sortedArray) {
root = buildRec(sortedArray, 0, sortedArray.length - 1);
}
private Node buildRec(int[] array, int start, int end) {
if (start > end) {
return null;
}
int mid = (start + end) / 2;
Node node = new Node(array[mid]);
node.left = buildRec(array, start, mid - 1);
node.right = buildRec(array, mid + 1, end);
return node;
}
public void inorderTraversal(Node node) {
if (node != null) {
inorderTraversal(node.left);
System.out.print(node.value + " ");
inorderTraversal(node.right);
}
}
}
智(지)! 德(덕)! 體(체)!