🛁 21278. 호석이 두 마리 치킨
문제
컴공 출신은 치킨집을 하게 되어있다. 현실을 부정하지 말고 받아들이면 마음이 편하다. 결국 호석이도 2050년에는 치킨집을 하고 있다. 치킨집 이름은 "호석이 두마리 치킨"이다.
이번에 키친 도시로 분점을 확보하게 된 호석이 두마리 치킨은 도시 안에 2개의 매장을 지으려고 한다. 도시는 N 개의 건물과 M 개의 도로로 이루어져 있다. 건물은 1번부터 N번의 번호를 가지고 있다. i 번째 도로는 서로 다른 두 건물 Ai 번과 Bi 번 사이를 1 시간에 양방향으로 이동할 수 있는 도로이다.
키친 도시에서 2개의 건물을 골라서 치킨집을 열려고 한다. 이 때 아무 곳이나 열 순 없어서 모든 건물에서의 접근성의 합을 최소화하려고 한다. 건물 X 의 접근성은 X 에서 가장 가까운 호석이 두마리 치킨집까지 왕복하는 최단 시간이다. 즉, "모든 건물에서 가장 가까운 치킨집까지 왕복하는 최단 시간의 총합"을 최소화할 수 있는 건물 2개를 골라서 치킨집을 열려고 하는 것이다.
컴공을 졸업한 지 30년이 넘어가는 호석이는 이제 코딩으로 이 문제를 해결할 줄 모른다. 알고리즘 퇴물 호석이를 위해서 최적의 위치가 될 수 있는 건물 2개의 번호와 그 때의 "모든 건물에서 가장 가까운 치킨집까지 왕복하는 최단 시간의 총합"을 출력하자. 만약 이러한 건물 조합이 여러 개라면, 건물 번호 중 작은 게 더 작을수록, 작은 번호가 같다면 큰 번호가 더 작을수록 좋은 건물 조합이다.
입력
첫 번째 줄에 건물의 개수 N과 도로의 개수 M 이 주어진다. 이어서 M 개의 줄에 걸쳐서 도로의 정보 Ai , Bi 가 공백으로 나뉘어서 주어진다. 같은 도로가 중복되어 주어지는 경우는 없다. 어떤 두 건물을 잡아도 도로를 따라서 오고 가는 방법이 존재함이 보장된다.
출력
한 줄에 건물 2개가 지어질 건물 번호를 오름차순으로 출력하고, 그때 모든 도시에서의 왕복 시간의 합을 출력한다.
만약 건물 조합이 다양하게 가능하면, 작은 번호가 더 작은 것을, 작은 번호가 같다면 큰 번호가 더 작은 걸 출력한다.
제한
2 ≤ N ≤ 100
N-1 ≤ M ≤ N×(N - 1)/2
1 ≤ Ai , Bi ≤ N (Ai ≠ Bi)
예제 입력 1
5 4
1 3
4 2
2 5
3 2
예제 출력 1
1 2 6
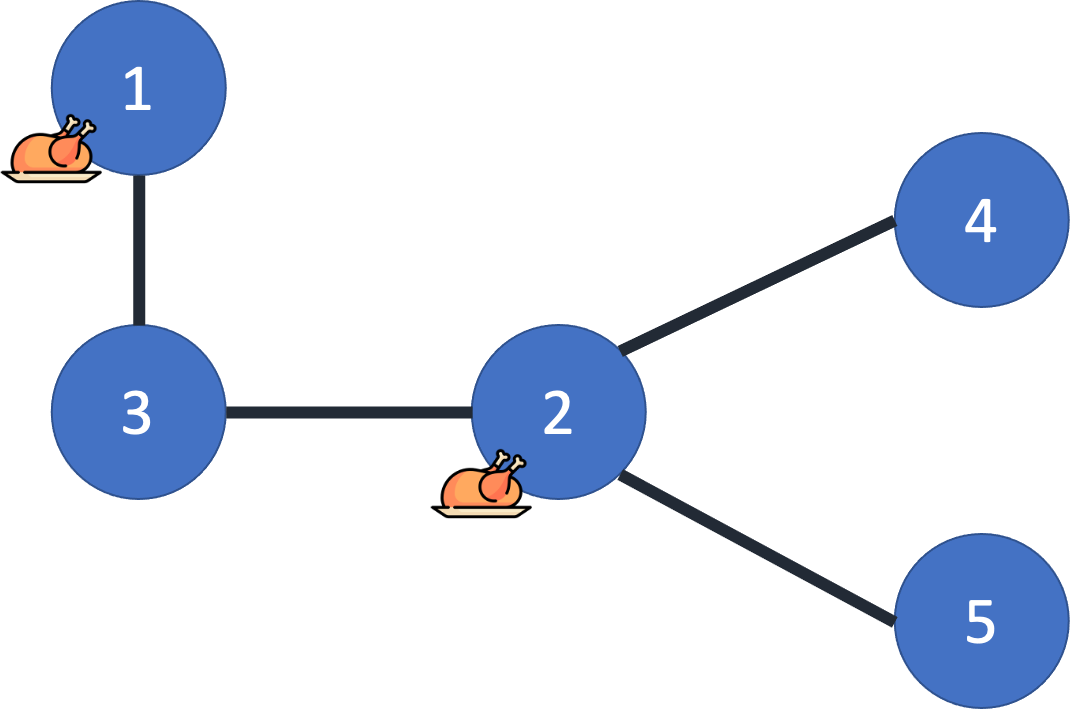
위의 그림과 같이 1번과 2번 건물에 치킨집을 짓게 되면 1번부터 5번 건물에 대해 치킨집까지의 왕복 시간이 0, 0, 2, 2, 2 로 최소가 된다. 2번과 3번 건물에 지어도 동일한 왕복 시간이 나오지만 더 작은 건물 번호를 출력해야 함을 유의하자.
알고리즘 분류
- 그래프 이론
- 브루트포스 알고리즘
- 그래프 탐색
- 너비 우선 탐색
- 플로이드–워셜
- 최단 경로
코드 - python3 성공
# 건물 N개, 도로 M개
# i번째 도로 = 서로 다른 두 건물 Ai 번과 Bi 번 사이를 1 시간에 양방향으로 이동할 수 있는 도로
# 2개의 건물을 골라 치킨집 오픈
# 모든 거물에서의 접근성의 합 최소화
# 접근성 = 가장 가까운 치킨집까지 왕복하는 최단 시간
# "모든 건물에서 가장 가까운 치킨집까지 왕복하는 최단 시간의 총합"을 최소화할 수 있는 건물 2개 선택
import sys
input = sys.stdin.readline
n, m = map(int, input().split()) # 건물 n, 도로 m
INF = int(1e9)
graph = [[INF] * (n + 1) for _ in range(n + 1)] # 그래프 초기화
# 도로 정보 입력
for _ in range(m):
a, b = map(int, input().split())
graph[a][b] = 1 # a -> b 가는 도로 존재
graph[b][a] = 1 # b -> a 가는 도로 존재
# 자기 자신은 초기화
for a in range(1, n + 1):
for b in range(1, n + 1):
if a == b:
graph[a][b] = 0 # 모든 건물로부터 자기 자신으로 가는 거리는 0으로 초기화
# 1. 모든 정점에서 모든 정점으로 가는 최소 거리 구하기
for k in range(1, n + 1): # 모든 건물 쌍 사이의 최단 거리 계산
for a in range(1, n + 1): # 출발 노드
for b in range(1, n + 1): # 도착 노드
graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b]) # 최단 거리 갱신
# 2. 2개의 건물을 선택하여(예상 치킨집) 모든 집을 방문해서 걸리는 거리를 측정
min_sum = INF
result = list()
for i in range(1, n): # 건물 2개를 뽑는다.
for j in range(2, n + 1):
sum_ = 0 # 모든 건물로부터의 접근성 합
for k in range(1, n + 1): # 모든 집을 방문하면서 거리를 측정
sum_ += min(graph[k][i], graph[k][j]) * 2 # k -> i, k -> j 중에 짧은 거리 합치기
if sum_ < min_sum:
min_sum = sum_
result = [i, j, sum_]
print(*result)🛁 1922. 네트워크 연결
문제
도현이는 컴퓨터와 컴퓨터를 모두 연결하는 네트워크를 구축하려 한다. 하지만 아쉽게도 허브가 있지 않아 컴퓨터와 컴퓨터를 직접 연결하여야 한다. 그런데 모두가 자료를 공유하기 위해서는 모든 컴퓨터가 연결이 되어 있어야 한다. (a와 b가 연결이 되어 있다는 말은 a에서 b로의 경로가 존재한다는 것을 의미한다. a에서 b를 연결하는 선이 있고, b와 c를 연결하는 선이 있으면 a와 c는 연결이 되어 있다.)
그런데 이왕이면 컴퓨터를 연결하는 비용을 최소로 하여야 컴퓨터를 연결하는 비용 외에 다른 곳에 돈을 더 쓸 수 있을 것이다. 이제 각 컴퓨터를 연결하는데 필요한 비용이 주어졌을 때 모든 컴퓨터를 연결하는데 필요한 최소비용을 출력하라. 모든 컴퓨터를 연결할 수 없는 경우는 없다.
입력
첫째 줄에 컴퓨터의 수 N (1 ≤ N ≤ 1000)가 주어진다.
둘째 줄에는 연결할 수 있는 선의 수 M (1 ≤ M ≤ 100,000)가 주어진다.
셋째 줄부터 M+2번째 줄까지 총 M개의 줄에 각 컴퓨터를 연결하는데 드는 비용이 주어진다. 이 비용의 정보는 세 개의 정수로 주어지는데, 만약에 a b c 가 주어져 있다고 하면 a컴퓨터와 b컴퓨터를 연결하는데 비용이 c (1 ≤ c ≤ 10,000) 만큼 든다는 것을 의미한다. a와 b는 같을 수도 있다.
출력
모든 컴퓨터를 연결하는데 필요한 최소비용을 첫째 줄에 출력한다.
예제 입력 1
6
9
1 2 5
1 3 4
2 3 2
2 4 7
3 4 6
3 5 11
4 5 3
4 6 8
5 6 8
예제 출력 1
23
힌트
이 경우에 1-3, 2-3, 3-4, 4-5, 4-6을 연결하면 주어진 output이 나오게 된다.
알고리즘 분류
- 그래프 이론
- 최소 스패닝 트리
코드 - python3 성공
import sys
input = sys.stdin.readline
N = int(input())
M = int(input())
def find_parent(x): # 부모 노드를 찾는 함수
if parent[x] != x:
parent[x] = find_parent(parent[x]) # 재귀 호출
return parent[x]
def union_parent(a, b): # 두 노드를 합치는 함수
a = find_parent(a) # 부모 노드 찾기
b = find_parent(b)
if a < b: # 두 노드 중 작은 번호를 가지는 노드를 부모로 설정
parent[b] = a
else:
parent[a] = b
parent = [i for i in range(N+1)]
edges = []
for _ in range(M):
a, b, c = map(int, input().split()) # 선 정보 컴퓨터A, 컴퓨터B, 비용C
edges.append((c, a, b))
edges.sort()
result = 0
for c, a, b in edges:
if find_parent(a) != find_parent(b): # 선이 연결하려는 두 컴퓨터가 같은 집합에 속하지 않는 경우
union_parent(a, b) # 두 컴퓨터 연결
result += c # 최소 비용 추가
print(result)🛁 1197. 최소 스패닝 트리
문제
그래프가 주어졌을 때, 그 그래프의 최소 스패닝 트리를 구하는 프로그램을 작성하시오.
최소 스패닝 트리는, 주어진 그래프의 모든 정점들을 연결하는 부분 그래프 중에서 그 가중치의 합이 최소인 트리를 말한다.
입력
첫째 줄에 정점의 개수 V(1 ≤ V ≤ 10,000)와 간선의 개수 E(1 ≤ E ≤ 100,000)가 주어진다. 다음 E개의 줄에는 각 간선에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 정점과 B번 정점이 가중치 C인 간선으로 연결되어 있다는 의미이다. C는 음수일 수도 있으며, 절댓값이 1,000,000을 넘지 않는다.
그래프의 정점은 1번부터 V번까지 번호가 매겨져 있고, 임의의 두 정점 사이에 경로가 있다. 최소 스패닝 트리의 가중치가 -2,147,483,648보다 크거나 같고, 2,147,483,647보다 작거나 같은 데이터만 입력으로 주어진다.
출력
첫째 줄에 최소 스패닝 트리의 가중치를 출력한다.
예제 입력 1
3 3
1 2 1
2 3 2
1 3 3
예제 출력 1
3
알고리즘 분류
- 그래프 이론
- 최소 스패닝 트리
풀이
- 크루스칼
코드 - python3 성공
import sys
input = lambda: sys.stdin.readline().rstrip()
V, E = map(int, input().split()) # 정점의 개수, 간선의 개수
# Kruskal Algorithm
edges = []
for _ in range(E):
A, B, C = map(int, input().split()) # 간선 정보
edges.append((A, B, C))
edges.sort(key=lambda x: x[2]) # C(Cost)가 적은 것부터 정렬
# Union-Find
parent = [i for i in range(V+1)] # 부모노드 초기화
def get_parent(x): # 부모 노드 찾는 함수
if parent[x] == x: # 부모 노드를 찾으면 경로 상의 모든 노드의 부모를 최상위 루트 노드로 갱신
return x
parent[x] = get_parent(parent[x]) # get_parent 거슬러 올라가면서 parent[x] 값도 갱신
return parent[x]
def union_parent(a, b): # 두 노드를 합치는 함수
a = get_parent(a)
b = get_parent(b)
if a < b: # 작은 쪽이 부모가 된다. (한 집합 관계라서 부모가 따로 있는 건 아님)
parent[b] = a
else:
parent[a] = b
def same_parent(a, b): # 두 노드의 부모가 같은지 확인하는 함수 \
return get_parent(a) == get_parent(b) # 부모가 같으면 같은 집합에 속함.
answer = 0
for a, b, cost in edges:
# cost가 작은 edge부터 하나씩 추가해가면서 같은 부모를 공유하지 않을 때(사이클 없을 때)만 확정
if not same_parent(a, b):
union_parent(a, b)
answer += cost
print(answer)🛁 11578. 팀원 모집
문제
2015년 11월 28일은 기다리고 기다리던 제1회 IUPC가 열리는 날이다. IUPC는 Inha University Programming Contest의 약자로 인하대학교 IT공대 학부생이면 누구나 참여할 수 있는 프로그래밍 경시대회이다.
IUPC의 총상금은 무려 110억 원이나 되며 고급스러운 점심과 많은 다과가 제공되어 참가자들이 대회에 집중할 수 있도록 최적의 환경을 제공한다. 그중 참가자들을 진정 열광시키는 것은 수많은 팀에게 추첨을 통해 문화상품권을 나눠준다는 점이다.
컴퓨터정보공학과에 재학 중인 강호는 대회에 참가하기 위해 팀원을 모집하려고 한다. IUPC가 여타 많은 대회와 다른 점이 있다면 문제의 수가 많고 팀원의 수가 무제한이라는 것이다. IUPC에서 모든 문제를 다 풀어 우승한 뒤 엄청난 부와 명예를 챙기고 싶은 강호는 모든 문제를 풀 수 있는 팀을 만들고 싶어 한다. 하지만 팀원의 수가 많으면 많을수록 자신에게 돌아오는 상금이 적어지기 때문에 최소한의 팀원으로 대회를 우승하고 싶어 한다.
강호가 선택할 수 있는 팀원의 목록과 각각의 팀원들이 해결할 수 있는 문제의 번호들이 주어졌을 때 강호가 IUPC에서 최소한의 팀원으로 모든 문제를 다 풀어 우승할 수 있도록 팀을 만들어보자.
입력
첫 번째 줄에 문제의 수 N과 강호가 팀원으로 고를 수 있는 학생들의 수 M이 공백을 구분으로 차례대로 주어진다. N과 M은 1이상 10이하의 자연수이다.
두 번째 줄부터 M개의 줄에 차례대로 i(1 ≤ i ≤ M)번 학생들이 풀 수 있는 문제의 개수 Oi와 i번 학생이 풀 수 있는 문제의 번호 Pij(1 ≤ j ≤ Oi, 1 ≤ Pij ≤ N)가 Oi개 주어진다.
출력
모든 문제를 풀 수 있으면서 팀원의 수가 가장 적은 팀을 구해 팀원의 수를 출력한다. 만약 모든 문제를 풀 수 있는 팀을 만들 수 없다면 -1을 출력한다,
예제 입력 1
5 4
2 3 4
2 1 2
4 1 2 3 4
1 5
예제 출력 1
2
힌트
3번 학생과 4번 학생을 선택하면 1번부터 5번까지 모든 문제를 풀 수 있는 팀을 만들 수 있다. 1번, 2번, 4번 학생을 선택해도 모든 문제를 다 풀 수 있지만 팀원의 수가 3명이라 답이 될 수 없다.
알고리즘 분류
- 브루트포스 알고리즘
- 비트마스킹
코드 - python3 성공
import sys
input = sys.stdin.readline
from itertools import combinations
n, m = map(int, input().split()) # 문제 수, 학생 수
s = [0] * m # 문제 해결 능력
answer = 0 # 모든 문제가 해결됨
flag = 0
for i in range(n): # 팀이 이기려면 모든 문제를 해결해야 함
answer |= (1 << i)
for i in range(m): # 학생의 문제 해결 능력에 대한 비트마스크 생성
tmp = (list(map(int, input().split())))
for j in tmp[1:]:
s[i] |= (1 << j - 1)
def find(): # 모든 문제를 해결하기 위해 필요한 최소 학생 수 탐색
for i in range(1, m + 1):
d = list(combinations(s, i)) # 각 팀 크기에 대해 가능한 모든 학생 조합을 생성
for probs in d:
tmp = 0
for prob in probs: # 각 조합에 대해 학생들의 문제 해결 능력의 합집합을 계산
tmp |= (prob)
if answer == tmp: # answer 비트 마스크오 같아면 모든 문제 해결
return i # 최소 학생 수로 팀 크기 반환
return -1
print(find())