2938. 3으로 나누어 떨어지지 않는 배열

문제

자연수로 이루어진 배열이 주어졌을 때, 수의 순서를 적절히 바꿔서 인접한 두 수의 합이 3으로 나누어 떨어지지 않는 배열을 만드는 프로그램을 작성하시오.

입력

첫째 줄에 배열의 크기 N이 주어진다. (1 ≤ N ≤ 10000)

둘째 줄에는 배열에 들어있는 수가 공백으로 구분되어 주어진다. 수는 1,000,000보다 작거나 같은 자연수이다.

출력

만약, 3으로 나누어 떨어지지 않게 배열을 만들 수 있다면 첫째 줄에 출력한다. 불가능하다면 -1을 출력한다.

예제 입력 1

3
1 2 3

예제 출력 1

2 3 1

예제 입력 2

5
4 6 3 9 8

예제 출력 2

3 4 6 8 9

예제 입력 3

6
3 7 6 4 2 8

예제 출력 3

3 7 4 6 2 8

예제 입력 4

3
3 12 9

예제 출력 4

-1

알고리즘 분류

• 해 구성하기
• 많은 조건 분기

코드1 - 메모리 초과

# https://slowsure.tistory.com/138

import sys
import itertools
input = sys.stdin.readline

n = int(input())
arr = list(map(int, input().split()))
per = list(itertools.permutations(arr, n))
per.sort()

# print(per)
# print(len(per))

answer = [-1]
bool = False

for i in range(len(per)):
    for j in range(n-1):
        if((per[i][j] + per[i][j+1])%3 == 0): # 3으로 나누어 떨어지면
            break
        elif(j == n-2): # 3으로 나누어 떨어지지 않으면서 j for문 끝까지 돌았을 때
            answer = per[i]
            bool = True
            break
    if(bool == True):
        break

for k in answer:
    print(k, end=" ")

---

8901. 화학 제품

문제

상근이는 각기 다른 병에 담긴 세 화학 물질 A, B, C를 가지고 있다. 두 화학 물질을 같은 양만큼 혼합하면, 화학 제품을 얻을 수 있다.

A와 B를 혼합하면 AB가 되고, B와 C를 혼합하면 BC, C와 A를 혼합하면 CA가 된다. (A 하나와 B 하나를 혼합하면 AB 하나를 얻게 된다) AB, BC, CA의 가격은 모두 다르다. 따라서, 만드는 화학 제품에 따라서 얻는 이익은 달라진다. 항상 정수 단위 만큼 두 화학 물질을 혼합할 수 있다.

예를 들어, A를 5만큼, B를 3만큼, C를 7만큼 가지고 있고, 각 화학 제품의 가격은 다음과 같은 경우를 생각해보자.

화학 제품	단위 가격
AB	$100
BC	$30
CA	$80

A 하나와 B하나를 혼합해 AB 하나를 만들면 $100을 얻게 된다. 그 다음 B 2개와 C 2개를 혼합하면 $60을 얻게 되고, C 4개와 A 4개를 혼합해 $320을 얻게 된다. 총 이익은 $480이 되고 이 이익이 가능한 이익 중 최댓값이다. 한 화학 물질은 모두 사용하지 않을 수도 있다. 이 예제에서는 C를 하나 사용하지 않았다.

다른 예로, A가 3개, B가 3개, C가 3개가 있고, AB, BC, CA의 가격이 모두 $100인 경우를 생각해보자. A 2개와 B 2개를 혼합해 $200을 얻고, B 1개와 C 1개를 혼합해 $100을 얻을 수 있다. 마지막으로 C 1개와 A 1개를 섞으면 $100을 얻는다. 총 이익은 $400이 되고, 이 값도 가능한 이익 중 최댓값이다.

상근이가 가지고 있는 A, B, C의 양과 AB, BC, CA의 가격이 주어졌을 때, 상근이가 얻을 수 있는 최대 이익을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 두 줄로 이루어져 있다. 첫째 줄에는 상근이가 가지고 있는 A, B, C의 양이 주어진다. 둘째 줄에는 AB, BC, CA의 가격이 주어진다. 입력으로 주어지는 모든 숫자는 정수이며, 1보다 크거나 같고, 1,000보다 작거나 같다.

출력

각 테스트 케이스 마다 최대 이익을 출력한다.

예제 입력 1

2
5 3 7
100 30 80
3 3 3
100 100 100

예제 출력 1

480
400

알고리즘 분류

• 브루트포스 알고리즘

코드1 - pypy 통과 / python 시간초과

# 세 화학 물질을 두개씩 혼합 가능
# 이익의 최댓값
# 가능한 모든 조합에 대해 이익을 계산하고 최대 이익 탐색

import sys
input = sys.stdin.readline

def max_profit(a, b, c, price):
    # 가능한 모든 조합에 대해 이익을 계산하고 최대 이익을 찾음
    max_price = 0
    for i in range(0, min(a,b)+1): # ab 화합물이 1개일때, 2개일때, 3개일때...
        for j in range(0, min(b-i,c)+1): # bc 화합물이 1개일때, 2개일때, 3개일때...
            k = min(a - i, c - j)  # ca 화합물은 남은 양만큼 사용
            max_price = max(max_price, i*price[0] + j*price[1] + k*price[2])

    return max_price

t = int(input())

for i in range(t):
    a, b, c = map(int, input().split())
    price = list(map(int, input().split()))

    result = max_profit(a, b, c, price)
    print(result)

---

11657. 타임머신

문제

N개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 버스가 M개 있다. 각 버스는 A, B, C로 나타낼 수 있는데, A는 시작도시, B는 도착도시, C는 버스를 타고 이동하는데 걸리는 시간이다. 시간 C가 양수가 아닌 경우가 있다. C = 0인 경우는 순간 이동을 하는 경우, C < 0인 경우는 타임머신으로 시간을 되돌아가는 경우이다.

1번 도시에서 출발해서 나머지 도시로 가는 가장 빠른 시간을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.

출력

만약 1번 도시에서 출발해 어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다. 그렇지 않다면 N-1개 줄에 걸쳐 각 줄에 1번 도시에서 출발해 2번 도시, 3번 도시, ..., N번 도시로 가는 가장 빠른 시간을 순서대로 출력한다. 만약 해당 도시로 가는 경로가 없다면 대신 -1을 출력한다.

예제 입력 1

3 4
1 2 4
1 3 3
2 3 -1
3 1 -2

예제 출력 1

4
3

예제 입력 2

3 4
1 2 4
1 3 3
2 3 -4
3 1 -2

예제 출력 2

-1

예제 입력 3

3 2
1 2 4
1 2 3

예제 출력 3

3
-1

알고리즘 분류

• 그래프 이론
• 최단 경로
• 벨만–포드

코드

import sys

input = sys.stdin.readline


def bf(start):
    # 시작 도시의 최단 시간을 0으로 초기화
    dist[start] = 0

    # 간선을 탐색하기 위한 for문. 간선은 n-1개여야 하므로 n번 반복
    for i in range(1, n + 1):
        # 각 도시에 대해 최단 거리 갱신을 위한 for문
        for a in range(1, n + 1):
            # 현재 도시에서 이동 가능한 도시와 걸리는 시간에 대해 반복
            for next, time in graph[a]:
                # 현재까지 계산된 최단 시간이 무한대가 아니고, 다음 도시로 가는 최단 시간이 현재까지의 최단 시간보다 작으면
                if dist[a] != float('inf') and dist[next] > dist[a] + time:
                    # 최단 시간 갱신
                    dist[next] = dist[a] + time
                    # n-1번 이후에도 값이 갱신되면 음수 사이클 존재
                    if i == n:
                        return True  # 음수 사이클 존재
    return False


# 도시 개수, 버스 개수 입력
n, m = map(int, input().split())
# 각 도시에서 이동 가능한 도시와 걸리는 시간을 저장하는 그래프 초기화
graph = [[] for i in range(n + 1)]
# 각 도시로 가는 최단 시간을 저장하는 리스트 초기화
dist = [float('inf') for i in range(n + 1)]

# 버스 노선 정보 입력 및 그래프 업데이트
for i in range(m):
    a, b, c = map(int, input().split())
    graph[a].append([b, c])

# 음수 사이클 여부 확인
negative_cycle = bf(1)

# 음수 사이클이 존재하면 -1 출력
if negative_cycle:
    print(-1)
else:
    # 각 도시로 가는 최단 시간 출력
    for i in range(2, n + 1):
        # 도시로 가는 경로가 없으면 -1 출력, 그렇지 않으면 해당 도시로 가는 최단 시간 출력
        if dist[i] == float('inf'):
            print(-1)
        else:
            print(dist[i])

---

인사고과

문제 설명

완호네 회사는 연말마다 1년 간의 인사고과에 따라 인센티브를 지급합니다. 각 사원마다 근무 태도 점수와 동료 평가 점수가 기록되어 있는데 만약 어떤 사원이 다른 임의의 사원보다 두 점수가 모두 낮은 경우가 한 번이라도 있다면 그 사원은 인센티브를 받지 못합니다. 그렇지 않은 사원들에 대해서는 두 점수의 합이 높은 순으로 석차를 내어 석차에 따라 인센티브가 차등 지급됩니다. 이때, 두 점수의 합이 동일한 사원들은 동석차이며, 동석차의 수만큼 다음 석차는 건너 뜁니다. 예를 들어 점수의 합이 가장 큰 사원이 2명이라면 1등이 2명이고 2등 없이 다음 석차는 3등부터입니다.

각 사원의 근무 태도 점수와 동료 평가 점수 목록 scores이 주어졌을 때, 완호의 석차를 return 하도록 solution 함수를 완성해주세요.

제한 사항

1 ≤ scores의 길이 ≤ 100,000
scores의 각 행은 한 사원의 근무 태도 점수와 동료 평가 점수를 나타내며 [a, b] 형태입니다.
scores[0]은 완호의 점수입니다.
0 ≤ a, b ≤ 100,000
완호가 인센티브를 받지 못하는 경우 -1을 return 합니다.

입출력 예

scores	result
[[2,2],[1,4],[3,2],[3,2],[2,1]]	4

입출력 예 설명

5 번째 사원은 3 번째 또는 4 번째 사원보다 근무 태도 점수와 동료 평가 점수가 모두 낮기 때문에 인센티브를 받을 수 없습니다. 2 번째 사원, 3 번째 사원, 4 번째 사원은 두 점수의 합이 5 점으로 최고점이므로 1 등입니다. 1 등이 세 명이므로 2 등과 3 등은 없고 1 번째 사원인 완호는 두 점수의 합이 4 점으로 4 등입니다.

코드

def solution(scores):
    answer = 0
    target_a, target_b = scores[0]
    target_score = target_a + target_b

    # 첫번째 점수에 대해서 내림차순,
    # 첫 번째 점수가 같으면 두 번째 점수에 대해서 오름차순으로 정렬합니다.
    scores.sort(key=lambda x: (-x[0], x[1]))
    maxb = 0

    for a, b in scores:
        if target_a < a and target_b < b:
            return -1

        if b >= maxb:
            maxb = b
            if a + b > target_score:
                answer += 1

    return answer + 1

---

1005. ACM Craft

문제

서기 2012년! 드디어 2년간 수많은 국민들을 기다리게 한 게임 ACM Craft (Association of Construction Manager Craft)가 발매되었다.

이 게임은 지금까지 나온 게임들과는 다르게 ACM크래프트는 다이나믹한 게임 진행을 위해 건물을 짓는 순서가 정해져 있지 않다. 즉, 첫 번째 게임과 두 번째 게임이 건물을 짓는 순서가 다를 수도 있다. 매 게임시작 시 건물을 짓는 순서가 주어진다. 또한 모든 건물은 각각 건설을 시작하여 완성이 될 때까지 Delay가 존재한다.

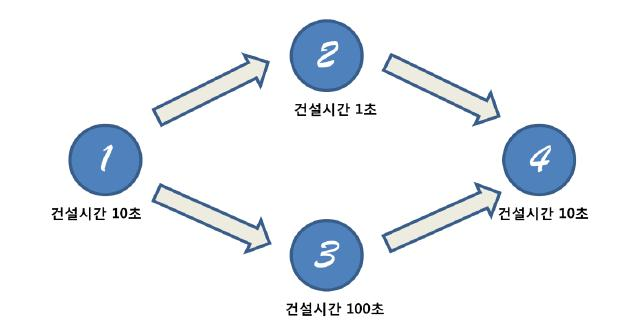
위의 예시를 보자.

이번 게임에서는 다음과 같이 건설 순서 규칙이 주어졌다. 1번 건물의 건설이 완료된다면 2번과 3번의 건설을 시작할수 있다. (동시에 진행이 가능하다) 그리고 4번 건물을 짓기 위해서는 2번과 3번 건물이 모두 건설 완료되어야지만 4번건물의 건설을 시작할수 있다.

따라서 4번건물의 건설을 완료하기 위해서는 우선 처음 1번 건물을 건설하는데 10초가 소요된다. 그리고 2번 건물과 3번 건물을 동시에 건설하기 시작하면 2번은 1초뒤에 건설이 완료되지만 아직 3번 건물이 완료되지 않았으므로 4번 건물을 건설할 수 없다. 3번 건물이 완성되고 나면 그때 4번 건물을 지을수 있으므로 4번 건물이 완성되기까지는 총 120초가 소요된다.

프로게이머 최백준은 애인과의 데이트 비용을 마련하기 위해 서강대학교배 ACM크래프트 대회에 참가했다! 최백준은 화려한 컨트롤 실력을 가지고 있기 때문에 모든 경기에서 특정 건물만 짓는다면 무조건 게임에서 이길 수 있다. 그러나 매 게임마다 특정건물을 짓기 위한 순서가 달라지므로 최백준은 좌절하고 있었다. 백준이를 위해 특정건물을 가장 빨리 지을 때까지 걸리는 최소시간을 알아내는 프로그램을 작성해주자.

입력

첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부터 N번까지 존재한다)

둘째 줄에는 각 건물당 건설에 걸리는 시간 D1, D2, ..., DN이 공백을 사이로 주어진다. 셋째 줄부터 K+2줄까지 건설순서 X Y가 주어진다. (이는 건물 X를 지은 다음에 건물 Y를 짓는 것이 가능하다는 의미이다)

마지막 줄에는 백준이가 승리하기 위해 건설해야 할 건물의 번호 W가 주어진다.

출력

건물 W를 건설완료 하는데 드는 최소 시간을 출력한다. 편의상 건물을 짓는 명령을 내리는 데는 시간이 소요되지 않는다고 가정한다.

건설순서는 모든 건물이 건설 가능하도록 주어진다.

제한

2 ≤ N ≤ 1000
1 ≤ K ≤ 100,000
1 ≤ X, Y, W ≤ N
0 ≤ Di ≤ 100,000, Di는 정수

예제 입력 1

2
4 4
10 1 100 10
1 2
1 3
2 4
3 4
4
8 8
10 20 1 5 8 7 1 43
1 2
1 3
2 4
2 5
3 6
5 7
6 7
7 8
7

예제 출력 1

120
39

예제 입력 2

5
3 2
1 2 3
3 2
2 1
1
4 3
5 5 5 5
1 2
1 3
2 3
4
5 10
100000 99999 99997 99994 99990
4 5
3 5
3 4
2 5
2 4
2 3
1 5
1 4
1 3
1 2
4
4 3
1 1 1 1
1 2
3 2
1 4
4
7 8
0 0 0 0 0 0 0
1 2
1 3
2 4
3 4
4 5
4 6
5 7
6 7
7

예제 출력 2

6
5
399990
2
0

코드

import sys
from collections import deque
input = sys.stdin.readline

# 테스트 케이스의 개수 T를 입력받음
t = int(input())

# 각 테스트 케이스에 대해 반복
for _ in range(t):
    # 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K를 입력받음
    n, k = map(int, input().rstrip().split())

    # 각 건물당 건설에 걸리는 시간 D1, D2, ..., DN을 입력받음
    d = list(map(int, input().rstrip().split()))

    # 건물간의 건설 순서를 저장할 그래프와 각 건물의 진입차수를 저장할 리스트 초기화
    graph = [[] for _ in range(n + 1)]
    inDegree = [0 for _ in range(n + 1)]

    # 각 건물의 건설시간을 저장할 리스트와 큐 초기화
    dp = [0 for _ in range(n + 1)]
    queue = deque()

    # 건설 순서를 입력받아 그래프와 진입차수를 설정
    for i in range(k):
        a, b = map(int, input().rstrip().split())
        graph[a].append(b)
        inDegree[b] += 1

    # 승리하기 위해 건설해야 할 건물의 번호 W를 입력받음
    w = int(input().rstrip())

    # 진입차수가 0인 건물을 큐에 추가하고 해당 건물의 건설시간을 초기화
    for i in range(1, n + 1):
        if inDegree[i] == 0:
            queue.append(i)
            dp[i] = d[i - 1]

    # 큐가 빌 때까지 반복
    while queue:
        # 현재 건물을 꺼냄
        tmp = queue.popleft()

        # 현재 건물과 연결된 건물들에 대해 진입차수를 감소시키고 건설시간을 업데이트
        for i in graph[tmp]:
            inDegree[i] -= 1
            dp[i] = max(dp[i], dp[tmp] + d[i - 1])

            # 만약 진입차수가 0이 되면 큐에 추가
            if inDegree[i] == 0:
                queue.append(i)

    # 승리하기 위해 건설해야 할 건물 W의 건설완료에 필요한 최소 시간 출력
    print(dp[w])