🎄 3987. 보이저 1호

문제

보이저 1호는 1977년에 발사된 NASA의 태양계 무인 탐사선이다. 현재 보이저 1호는 태양권덮개 (헬리오시스)에 있다.

보이저 1호와 같이 오랜 기간동안 활동하는 탐사선은 경로를 항성계를 만날 때 마다 라디오 시그널 메시지를 이용해서 기록하고 있다.

항성계를 N * M개의 직사각형으로 나누어져 있는 N행 M열의 직사각형 그리드라고 생각해보자. 각 칸은 행성, 블랙홀을 포함할 수 있으며, 비어있을 수도 있다. 탐사선은 인접한 네 칸(위, 아래, 오른쪽, 왼쪽)중에서 하나를 골라서 시그널을 보낸다.

시그널은 항상 일직선으로 전파되며, 행성을 만났을 경우에는 전파되는 방향이 90도로 바뀌게 된다. 행성은 '/'와 '\'로 표현되는 두 종류가 있으며, 반사되는 법칙은 아래 그림과 같다.

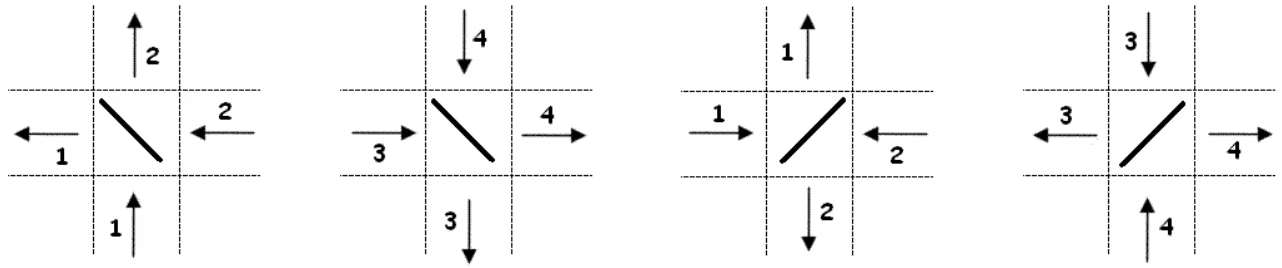
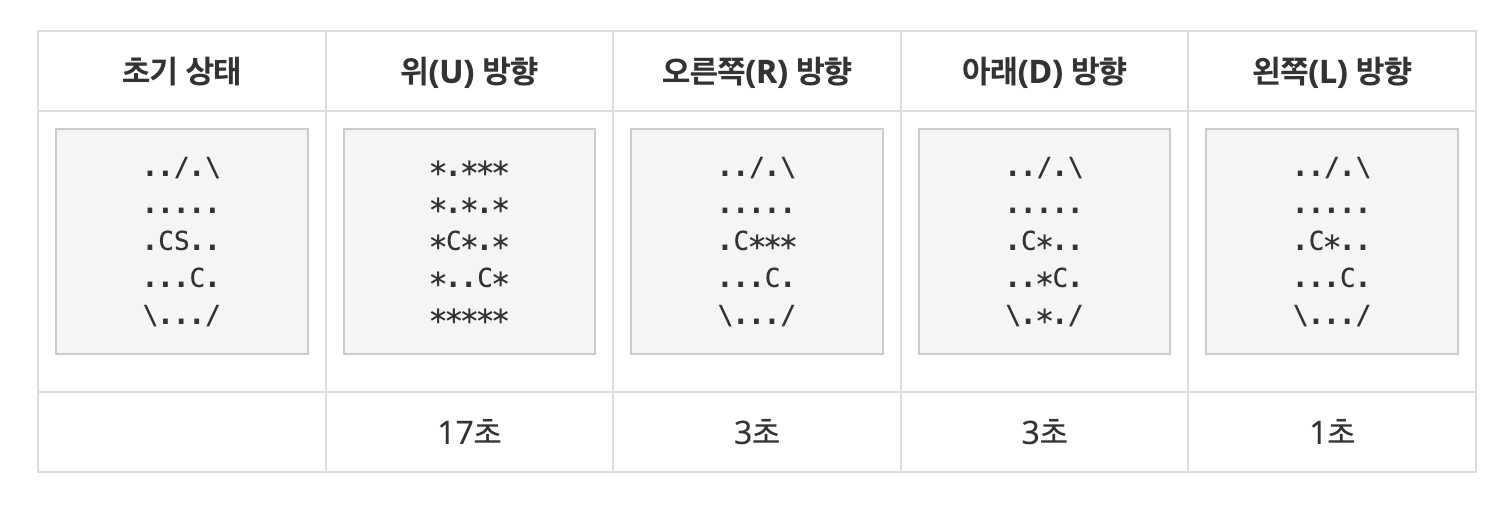
시그널이 블랙홀이 있는 칸을 만나거나 항성계를 벗어날 때 까지 계속 전파된다. 시그널이 인접한 칸으로 이동하는데 걸리는 시간은 1초이다.

탐사선이 어느 방향으로 시그널을 보내면, 시그널이 항성계 내부에 있는 시간이 최대가 되는지 구하는 프로그램을 작성하시오.

입력

첫째 줄에 N과 M이 주어진다. (1 ≤ N, M ≤ 500)

다음 N개 줄에는 M개의 문자가 주어지며, '/'와 '\'는 행성을, C는 블랙홀을, '.'는 빈 칸을 나타낸다.

마지막 줄에는 탐사선이 있는 위치 PR과 PC가 주어진다. (1 ≤ PR ≤ N, 1 ≤ PC ≤ M)

출력

첫째 줄에 시그널을 보내는 방향을 출력한다. (U: 위, R: 오른쪽, D: 아래, L: 왼쪽)

만약, 방향이 여러 가지가 존재한다면, U, R, D, L의 순서 중 앞서는 것을 출력한다.

둘째 줄에는 가장 긴 시간을 출력한다. 만약, 시그널이 항성계 내에서 무한히 전파될 수 있다면 "Voyager"를 출력한다.

예제 입력 1

5 5
../.\
.....
.C...
...C.
.../
3 3

예제 출력 1

U
17

예제 입력 2

5 5
....\
...
./..
../C
.../
1 1

예제 출력 2

D
12

예제 입력 3

5 7
/.....\
../...
...../
/.....\
..../
3 3

예제 출력 3

R
Voyager

힌트

알고리즘 분류

• 구현
• 그래프 이론
• 그래프 탐색
• 시뮬레이션

코드 - python3 성공

import sys

input = sys.stdin.readline

direction = ("U", "R", "D", "L")
dr = (-1, 0, 1, 0)
dc = (0, 1, 0, -1)
P, Q = (1, 0, 3, 2), (3, 2, 1, 0)

N, M = map(int, input().split())
A = [["C"] * (M + 2)]  # 블랙홀로 둘러싸기
for _ in range(N):
    A.append(["C"] + list(input().strip()) + ["C"])
A.append(["C"] * (M + 2))
sr, sc = map(int, input().split())


def solve():
    max_time, max_dir = 0, 0
    for sd in range(4):
        r, c, d, time = sr, sc, sd, 1  # 시작 위치, 시작 방향, 이동 시간
        while True:
            # 블랙홀 만났거나 항성계 벗어나면
            if A[r + dr[d]][c + dc[d]] == "C":
                break

            r += dr[d]
            c += dc[d]

            # 방향 전환
            if A[r][c] == "/":
                d = P[d]
            elif A[r][c] == "\\":
                d = Q[d]
            time += 1

            # 처음 출발한 지점을 동일한 방향으로 접근한 경우 무한 루프
            if (r, c, d) == (sr, sc, sd):
                print(direction[sd])
                print("Voyager")
                return

        # 값이 클 때만 이동 시간, 현재 방향 갱신
        if max_time < time:
            max_time = time
            max_dir = sd

    print(direction[max_dir])
    print(max_time)


solve()

---

🎄 22867. 종점

문제

주행을 마친 버스들이 종점에 들어온다. 종점에 들어온 버스는 버스를 정비하기 위한 자리에 들어간다. 즉, 종점에 버스 4대가 있다면 버스를 정비할 수 있는 공간이 최소 4개 이상 필요하다. 만약 같은 시각에 종점에 들어오는 버스 A와 종점에서 출발하는 버스 B가 있을 경우는 버스 B가 먼저 종점에서 출발하고 그 다음으로 버스 A가 종점으로 들어온다.

버스의 시간표가 매일 동일하며 종점에 들어오는 시각과 나가는 시각이 매일 동일하다.

이번에 버스 시간표가 변경이 되어 버스를 정비하는 공간이 최소 몇 개 이상 필요한지 다시 계산을 해야한다. 이를 도와 계산을 해주자.

입력

첫 번째 줄에는 종점에 들어오는 버스들의 개수
$N$이 주어진다.

두 번째 줄부터
$N+1$번째 줄까지 각 버스가 종점에 들어오는 시각과 종점에서 나가는 시각이 주어진다. 한 버스의 나가는 시각은 들어오는 시각보다 늦다.

주어지는 시각의 형식은 다음과 같다. HH:MM:SS.sss (HH는 시각을, MM은 분, SS은 초, sss 밀리초를 의미한다.)

출력

버스 정비를 위한 공간이 최소 몇 개 이상 필요한지 출력한다.

제한

• $1 ≤ N ≤ 100,000$ 
• $0 ≤ HH < 24$ 
• $0 ≤ MM < 60$ 
• $0 ≤ SS < 60$ 
• $0 ≤ sss < 1000$ 

예제 입력 1

4
06:00:00.000 06:30:00.000
06:10:45.000 06:15:00.000
06:30:00.000 06:40:00.000
06:01:00.001 06:40:00.001

예제 출력 1

3

알고리즘 분류

• 문자열
• 정렬
• 스위핑

코드 - 답은 맞는데 런타임에러

import sys
from collections import deque

input = sys.stdin.readline

def time_to_int(time_str):
    time_parts = time_str.split(':')
    hours, minutes, seconds = map(int, time_parts[:-1])  # Extract hours, minutes, and seconds
    milliseconds = int(time_parts[-1].split('.')[0])  # Extract milliseconds
    return hours * 3600 + minutes * 60 + seconds + milliseconds / 1000

def calculate_min_spaces(n, bus_schedule):
    bus_schedule.sort(key=lambda x: x[0])
    spaces_deque = deque()

    for start_time, end_time in bus_schedule:
        start_int = time_to_int(start_time)
        end_int = time_to_int(end_time)

        while spaces_deque and start_int >= spaces_deque[0]:
            spaces_deque.popleft()

        spaces_deque.append(end_int)

    return len(spaces_deque)

# 입력 받기
n = int(input())
bus_schedule = [tuple(map(str, input().split())) for _ in range(n)]

# 결과 출력
result = calculate_min_spaces(n, bus_schedule)
print(result)

---

🎄 9252. LCS 2

문제

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

입력

첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.

출력

첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를, 둘째 줄에 LCS를 출력한다.

LCS가 여러 가지인 경우에는 아무거나 출력하고, LCS의 길이가 0인 경우에는 둘째 줄을 출력하지 않는다.

예제 입력 1

ACAYKP
CAPCAK

예제 출력 1

4
ACAK

알고리즘 분류

• 다이나믹 프로그래밍

코드 - 답은 맞는데 런타임에러

import sys
input = sys.stdin.readline

N = 1001
s = [[0] * N for _ in range(N)] # DP테이블 초기화

a = input()
b = input()

def print_lcs(i, j): # LCS 출력 재귀 함수
    if s[i][j] == 0: # LCS 길이가 0이라면 함수 종료
        return
    if a[i - 1] == b[j - 1]: # 현재 위치에서 문자가 일치하는 경우
        print_lcs(i - 1, j - 1) # 현재 위치의 문자를 출력
        print(a[i - 1], end="") # 대각선 위치로 이동하여 재귀 호출
    else: # 현재 위치에서 문자가 일치하지 않는 경우
        print_lcs(i - 1, j) if s[i - 1][j] > s[i][j - 1] else print_lcs(i, j - 1) # 조건 만족시 위쪾으로 이동, 그렇지 않으면 왼쪽으로 이동

i = 0
j = 0
for i in range(len(a)): # a 문자열 탐색
    for j in range(len(b)): # b 문자열 탐색
        if a[i] == b[j]: # 두 문자가 일치하는 경우
            s[i + 1][j + 1] = s[i][j] + 1 # 이전 대각선 값 + 1
        else: # 일치하지 않는 경우
            s[i + 1][j + 1] = max(s[i][j + 1], s[i + 1][j]) # 이전 행과 열 중에서 더 큰 값

print(s[i][j])
print_lcs(i, j)

---

🎄 2314. 이세계 게임

문제

트럭 운전사 택희는 오랜 기간 동안의 공로를 인정받아 이세계로 소환되었다. 택희가 소환된 이세계에는 천사 종족 Portableangel과 악마 종족 Legnaelbatrop이 살고 있었다. 택희는 뛰어난 알고리즘 지식을 발휘해 얼마 지나지 않아 두 종족을 모두 지배하는 이세계의 왕이 되었다.

폭군 택희는 지루해지면 이세계의 주민들을 이용해 게임을 한다. 먼저 종족과 무관하게 16명의 개체를 모아서 4×4 격자 형태로 세워 놓는다. 그 다음 각 자리에 어떤 종족이 서야 하는지를 지정해 주고, 그에 맞게 다시 서도록 명령한다. 그러면 이들은 서로 자리를 바꿔서 택희가 원하는 배치를 만들어야 한다. 자리를 바꿀 때는 상하좌우로 인접한 두 개체끼리만 바꿀 수 있으며, 한 개체가 여러 번 자리를 바꿀 수도 있다.

현재 주민들의 배치와 택희가 원하는 배치가 주어질 때, 최소 몇 번의 자리 바꿈이 필요한지 구하여라.

입력

'P' 또는 'L'을 값으로 갖는 4×4 행렬이 공백 없이 주어진다. 이는 현재 주민들의 배치를 나타내며, 'P'는 Portableangel, 'L'은 Legnaelbatrop 종족을 뜻한다.

그 다음 빈 줄이 0개 이상 주어진 뒤 택희가 원하는 배치가 같은 방식으로 주어진다. 택희에게는 최소한의 양심이 있기에 불가능한 배치는 주어지지 않는다.

출력

택희가 원하는 배치를 만들기 위해 필요한 최소 자리 바꿈 횟수를 출력한다.

예제 입력 1

LLLL
PPPP
LLLP
PPLP

LPLP
PLPL
LPLP
PLPL

예제 출력 1

4

알고리즘 분류

• 그래프 이론
• 그래프 탐색
• 너비 우선 탐색
• 비트마스킹

코드 - 답은 맞는데 런타임에러

import sys
from collections import deque

input = sys.stdin.readline

# 배열을 문자열 '1011011010111111'로 변환
def arr2bit(arr):
    bit = ''
    for i in range(4):
        for j in range(4):
            bit += arr[i][j]
    return bit

# 문자열을 4*4 배열로 변환
def bit2arr(bit):
    arr = []
    for i in range(4):
        arr.append(list(bit[i * 4:(i + 1) * 4]))
    return arr

inputs = []
while len(inputs) < 8:  # input 데이터의 공백 처리
    tmp = input().strip()
    if tmp:
        inputs.append(list(tmp))

current_board = inputs[:4]
target_board = inputs[4:]

trans = {
    'L': '0',
    'P': '1'
}
for i in range(4):
    for j in range(4):
        current_board[i][j] = trans[current_board[i][j]]
        target_board[i][j] = trans[target_board[i][j]]

targetbit = arr2bit(target_board)  # 목표값
startbit = arr2bit(current_board)  # 시작값

Q = deque()
Q.append(startbit)

# 방문처리 dictionary로
visited = dict()
visited[startbit] = 0  # count로 활용
while Q:
    bit = Q.popleft()
    board = bit2arr(bit)
    # 목표값과 비교
    if bit == targetbit:
        ans = visited[bit]
        break
    # 수평교환
    for i in range(4):
        for j in range(3):
            if board[i][j] != board[i][j + 1]:
                board[i][j], board[i][j + 1] = board[i][j + 1], board[i][j]
                # 2차원 배열 -> 문자열
                newbit = arr2bit(board)
                if not visited.get(newbit):
                    visited[newbit] = visited[bit] + 1
                    Q.append(newbit)
                board[i][j], board[i][j + 1] = board[i][j + 1], board[i][j]

    # 수직교환
    for i in range(3):
        for j in range(4):
            if board[i][j] != board[i + 1][j]:
                board[i][j], board[i + 1][j] = board[i + 1][j], board[i][j]
                # 2차원 배열 -> 문자열
                newbit = arr2bit(board)
                if not visited.get(newbit):
                    visited[newbit] = visited[bit] + 1
                    Q.append(newbit)
                board[i][j], board[i + 1][j] = board[i + 1][j], board[i][j]

# 출력
print(ans)

---

🎄 11066. 파일 합치기

문제

소설가인 김대전은 소설을 여러 장(chapter)으로 나누어 쓰는데, 각 장은 각각 다른 파일에 저장하곤 한다. 소설의 모든 장을 쓰고 나서는 각 장이 쓰여진 파일을 합쳐서 최종적으로 소설의 완성본이 들어있는 한 개의 파일을 만든다. 이 과정에서 두 개의 파일을 합쳐서 하나의 임시파일을 만들고, 이 임시파일이나 원래의 파일을 계속 두 개씩 합쳐서 소설의 여러 장들이 연속이 되도록 파일을 합쳐나가고, 최종적으로는 하나의 파일로 합친다. 두 개의 파일을 합칠 때 필요한 비용(시간 등)이 두 파일 크기의 합이라고 가정할 때, 최종적인 한 개의 파일을 완성하는데 필요한 비용의 총 합을 계산하시오.

예를 들어, C1, C2, C3, C4가 연속적인 네 개의 장을 수록하고 있는 파일이고, 파일 크기가 각각 40, 30, 30, 50 이라고 하자. 이 파일들을 합치는 과정에서, 먼저 C2와 C3를 합쳐서 임시파일 X1을 만든다. 이때 비용 60이 필요하다. 그 다음으로 C1과 X1을 합쳐 임시파일 X2를 만들면 비용 100이 필요하다. 최종적으로 X2와 C4를 합쳐 최종파일을 만들면 비용 150이 필요하다. 따라서, 최종의 한 파일을 만드는데 필요한 비용의 합은 60+100+150=310 이다. 다른 방법으로 파일을 합치면 비용을 줄일 수 있다. 먼저 C1과 C2를 합쳐 임시파일 Y1을 만들고, C3와 C4를 합쳐 임시파일 Y2를 만들고, 최종적으로 Y1과 Y2를 합쳐 최종파일을 만들 수 있다. 이때 필요한 총 비용은 70+80+150=300 이다.

소설의 각 장들이 수록되어 있는 파일의 크기가 주어졌을 때, 이 파일들을 하나의 파일로 합칠 때 필요한 최소비용을 계산하는 프로그램을 작성하시오.

입력

프로그램은 표준 입력에서 입력 데이터를 받는다. 프로그램의 입력은 T개의 테스트 데이터로 이루어져 있는데, T는 입력의 맨 첫 줄에 주어진다.각 테스트 데이터는 두 개의 행으로 주어지는데, 첫 행에는 소설을 구성하는 장의 수를 나타내는 양의 정수 K (3 ≤ K ≤ 500)가 주어진다. 두 번째 행에는 1장부터 K장까지 수록한 파일의 크기를 나타내는 양의 정수 K개가 주어진다. 파일의 크기는 10,000을 초과하지 않는다.

출력

프로그램은 표준 출력에 출력한다. 각 테스트 데이터마다 정확히 한 행에 출력하는데, 모든 장을 합치는데 필요한 최소비용을 출력한다.

예제 입력 1

2
4
40 30 30 50
15
1 21 3 4 5 35 5 4 3 5 98 21 14 17 32

예제 출력 1

300
864

알고리즘 분류

• 다이나믹 프로그래밍

코드 - python3 시간초과 / pypy 성공

import sys
input = sys.stdin.readline

t = int(input())

for _ in range(t):
    k = int(input())
    arr = [0] + list(map(int, input().split()))  # 각 파일의 비용을 담고 있는 리스트
    s = [0] * (k + 1)  # 각 비용을 이용한 부분합을 담고 있는 리스트

    s[1] = arr[1]
    for i in range(2, k + 1):
        s[i] = s[i - 1] + arr[i]
    # 이렇게 넣어놓으면 i부터 j까지의 합을 s[j] - s[i-1]로 구할 수 있다.

    dp = [[0] * (k + 1) for _ in range(k + 1)]
    # dp[i][j]는 i번째 파일부터 j번째 파일까지를 합치는 데 필요한 최소 비용을 담고 있다
    # 즉 우리가 구해야 하는 것은 dp[1][n]

    for n in range(2, k + 1):  # 길이. 최대 k까지 돌아야 하므로 range는 2, k+1
        for i in range(1, k - n + 2):  # 시작 위치. 길이가 n일때 1,2,...n 부터 시작해서 k-(n-1),...k-1,k까지 돈다.
            # 예를 들어 길이가 2면 k-1까지 돌아야한다.

            dp[i][i + n - 1] = min(dp[i][j] + dp[j + 1][i + n - 1] for j in range(i, i + n - 1)) + (
                        s[i + n - 1] - s[i - 1])
            # j는 중간에 잘리는 위치. (i, i+n-1) 에서 j가 될 수 있는 것은 i부터 i+n-2까지.
            # 그리고 뒤에 i부터 i+n-1까지의 부분합을 더해준다. (s 리스트 이용)

    print(dp[1][k])

---

🎄 pro3. 자물쇠와 열쇠

문제 설명

고고학자인 "튜브"는 고대 유적지에서 보물과 유적이 가득할 것으로 추정되는 비밀의 문을 발견하였습니다. 그런데 문을 열려고 살펴보니 특이한 형태의 자물쇠로 잠겨 있었고 문 앞에는 특이한 형태의 열쇠와 함께 자물쇠를 푸는 방법에 대해 다음과 같이 설명해 주는 종이가 발견되었습니다.

잠겨있는 자물쇠는 격자 한 칸의 크기가 1 x 1인 N x N 크기의 정사각 격자 형태이고 특이한 모양의 열쇠는 M x M 크기인 정사각 격자 형태로 되어 있습니다.

자물쇠에는 홈이 파여 있고 열쇠 또한 홈과 돌기 부분이 있습니다. 열쇠는 회전과 이동이 가능하며 열쇠의 돌기 부분을 자물쇠의 홈 부분에 딱 맞게 채우면 자물쇠가 열리게 되는 구조입니다. 자물쇠 영역을 벗어난 부분에 있는 열쇠의 홈과 돌기는 자물쇠를 여는 데 영향을 주지 않지만, 자물쇠 영역 내에서는 열쇠의 돌기 부분과 자물쇠의 홈 부분이 정확히 일치해야 하며 열쇠의 돌기와 자물쇠의 돌기가 만나서는 안됩니다. 또한 자물쇠의 모든 홈을 채워 비어있는 곳이 없어야 자물쇠를 열 수 있습니다.

열쇠를 나타내는 2차원 배열 key와 자물쇠를 나타내는 2차원 배열 lock이 매개변수로 주어질 때, 열쇠로 자물쇠를 열수 있으면 true를, 열 수 없으면 false를 return 하도록 solution 함수를 완성해주세요.

제한사항

• key는 M x M(3 ≤ M ≤ 20, M은 자연수)크기 2차원 배열입니다.
• lock은 N x N(3 ≤ N ≤ 20, N은 자연수)크기 2차원 배열입니다.
• M은 항상 N 이하입니다.
• key와 lock의 원소는 0 또는 1로 이루어져 있습니다.
  • 0은 홈 부분, 1은 돌기 부분을 나타냅니다.

입출력 예

key	lock	result
[[0, 0, 0], [1, 0, 0], [0, 1, 1]]	[[1, 1, 1], [1, 1, 0], [1, 0, 1]]	true

입출력 예에 대한 설명

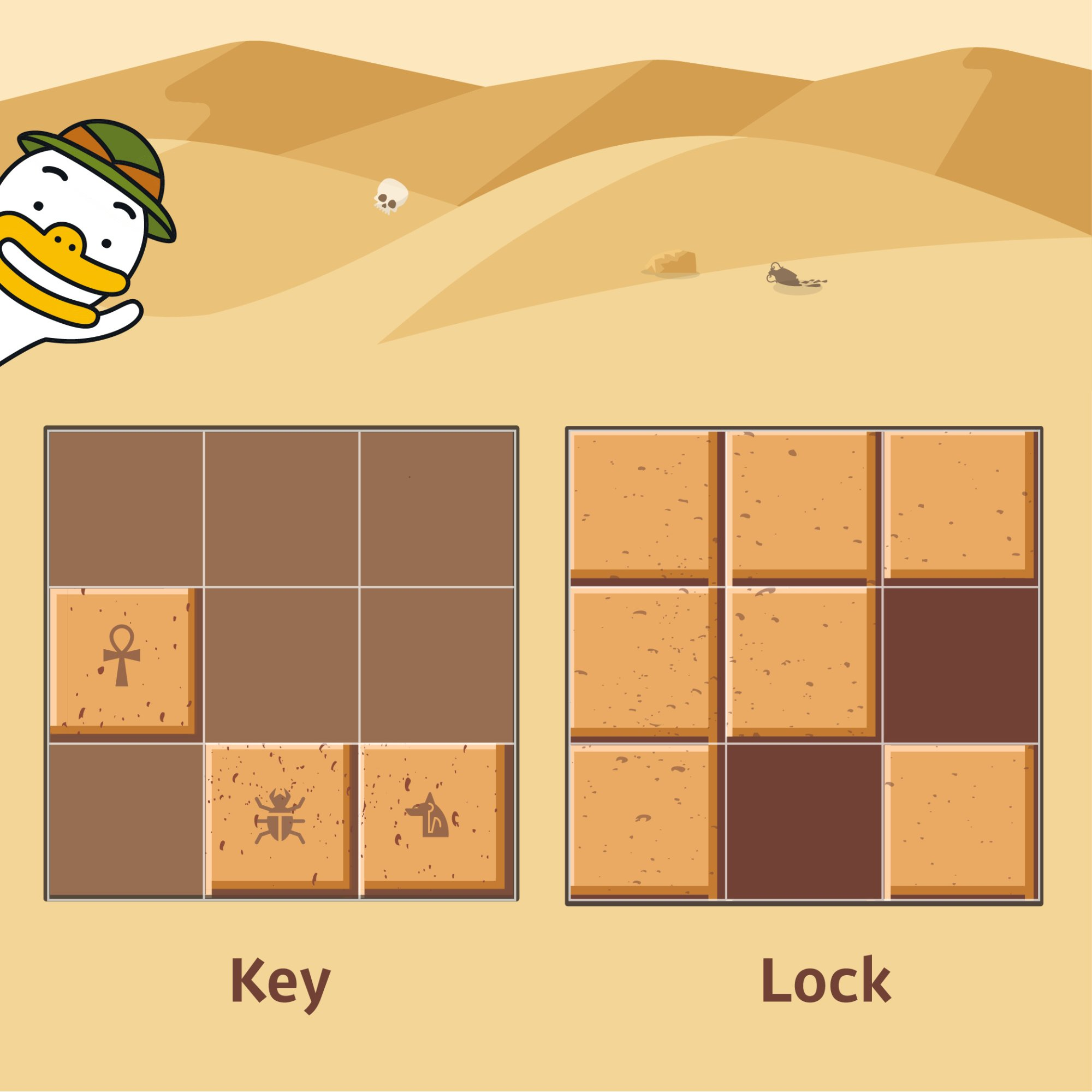
key를 시계 방향으로 90도 회전하고, 오른쪽으로 한 칸, 아래로 한 칸 이동하면 lock의 홈 부분을 정확히 모두 채울 수 있습니다.

코드

# 자물쇠와 열쇠

# NxN 2차원 리스트 d도 회전
# 회전 각도 d => 1: 90도, 2: 180도, 3: 270도
def rotate(array, d):
    n = len(array)  # 배열의 길이
    result = [[0] * n for _ in range(n)]

    if d % 4 == 1:
        for r in range(n):
            for c in range(n):
                result[c][n - r - 1] = array[r][c]
    elif d % 4 == 2:
        for r in range(n):
            for c in range(n):
                result[n - r - 1][n - c - 1] = array[r][c]
    elif d % 4 == 3:
        for r in range(n):
            for c in range(n):
                result[n - c - 1][r] = array[r][c]
    else:
        for r in range(n):
            for c in range(n):
                result[r][c] = array[r][c]

    return result


# 자물쇠 중간 NxN 부분이 모두 1인지 확인
def check(new_lock):
    n = len(new_lock) // 3
    for i in range(n, n * 2):
        for j in range(n, n * 2):
            if new_lock[i][j] != 1:
                return False
    return True


def solution(key, lock):
    m = len(key)
    n = len(lock)
    # 기존 자물쇠보다 3배 큰 자물쇠
    new_lock = [[0] * (n * 3) for _ in range(n * 3)]
    # 새로운 자물쇠의 중앙 부분에 기존 자물쇠 넣기
    for i in range(n):
        for j in range(n):
            new_lock[n + i][n + j] = lock[i][j]

    # 열쇠를 (1, 1)부터 (N*2, N*2)까지 이동시키며 확인
    for i in range(1, n * 2):
        for j in range(1, n * 2):
            # 열쇠를 0, 90, 180, 270도로 회전시키며 확인
            for d in range(4):
                r_key = rotate(key, d)  # key를 d만큼 회전시킨 리스트
                for x in range(m):
                    for y in range(m):
                        new_lock[i + x][j + y] += r_key[x][y]

                if check(new_lock):
                    return True

                for x in range(m):
                    for y in range(m):
                        new_lock[i + x][j + y] -= r_key[x][y]

    return False