LCS 알고리즘이란?
❗ LCS는 Longest Common Subsequence의 줄임말로, 공통 부분 문자열 중 가장 길이가 긴 문자열을 말합니다.
이 때, Substring과 Subsequence와의 차이점을 보고 넘어가겠습니다.
- SubString: 전체 문자열에서 연속된 부분 문자열
- ex) ABCDEFG 에서 Substring은 ABC, DEFG, ABCDEF, ... 등이 있다.
- Subsequence: 전체 문자열에서 꼭 연속된 문자열인 것은 아닌 부분 문자열
- ex) ABCDEFGH 에서 Subsequence는 ABD, AEFGH, AFI, ... 등이 있다.
- 단, 앞에서부터가 아니라 순서가 뒤바뀐 IHE, BIDEHF 와 같은 문자열은 부분 문자열이 될 수 없다.

두 가지 구하는 방식 전부 확인해볼 것인데, 일단 먼저 최장 공통 문자열(Substring)부터 확인을 해봅시다.
최장 공통 문자열(Longest Common Substring)
이 방식이 더 쉽고, 이것 이후에 보는 최장 공통 부분수열은 이것의 확장판이라고 생각할 수 있습니다.
먼저, 점화식을 적어보자면 다음과 같습니다.
if i == 0 or j == 0: # 마진 설정 (빈영역 설정)
LCS[i][j] = 0
else if string_A[i - 1] == string_B[j - 1]:
LCS[i][j] = LCS[i - 1][j - 1] + 1
else:
LCS[i][j] = 0LCS: 2차원 배열로, 두개의 string의 길이를 각각 배열의 크기로 가지는 배열
최장 공통 문자열의 점화식을 간단한 로직을 보여주는 코드로서 확인을 해봤습니다.
i와 j는 당연히 각각 String의 Index값이라고 생각할 수 있습니다.
참고로 Index값인데 i - 1, j - 1을 비교하는 이유는 String앞에 빈 문자열을 설정해두기 위함입니다.
그렇게 함으로서 LCS[i - 1][j - 1]을 처리할 때 조건문을 굳이 사용할 필요가 사라졌습니다.
최종적으로 배열 안에서 가장 높은 Value값을 가지고 있는 것이 최장 공통 문자열의 길이라고 볼 수 있겠네요.
직관적으로 보기 위해서 아래의 그림을 참고합시다.

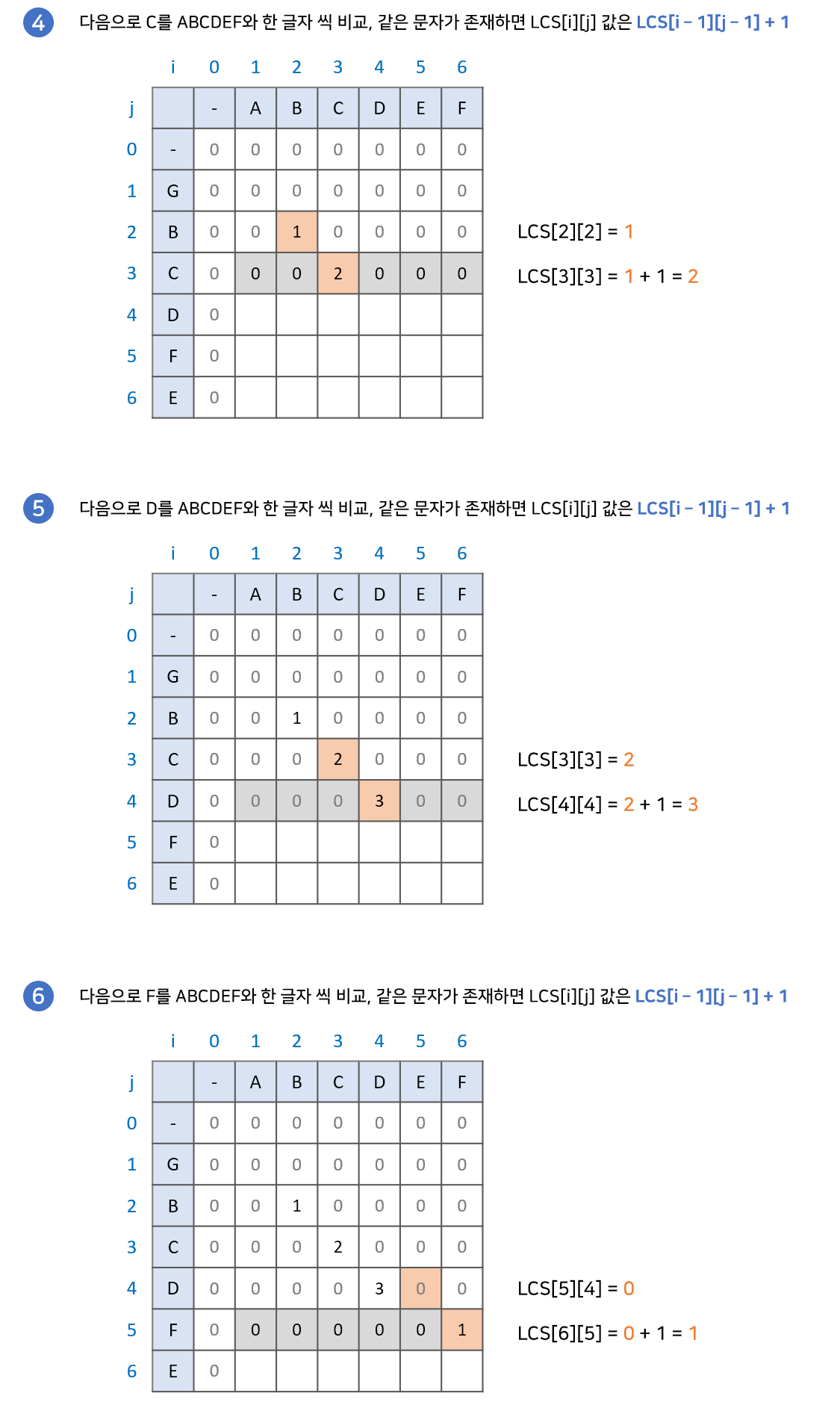
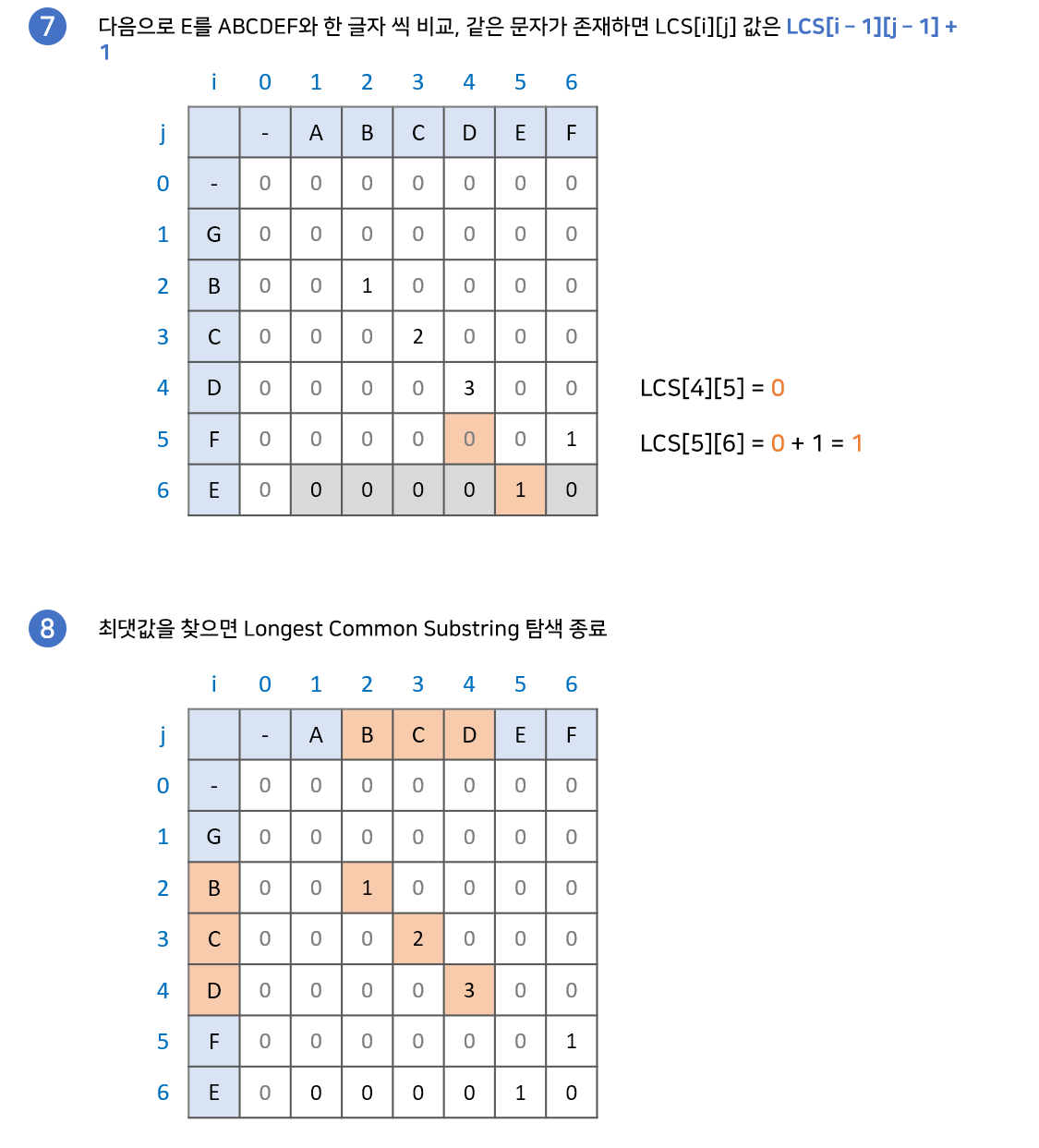
최장 공통 부분수열(Longest Common Subsequence)
최장 공통 부분수열의 경우 어떻게 구해야 할까요?
앞서 봤던 최장 공통 문자열의 경우 연속해서 나오는 문자열을 확인할 때 앞에서 나온 문자열의 일치 여부를 value로 통해 확인했습니다.
그렇다면, 최장 공통 부분수열의 경우에는 앞에서 나온 문자를 떨어져 있는 뒤의 문자도 이용할 수 있도록 해야합니다.
점화식은 다음과 같습니다.
if i == 0 or j == 0:
LCS[i][j] = 0
else if String_A[i - 1] == String_B[j - 1]:
LCS[i][j] = LCS[i - 1][j - 1] + 1
else :
LCS[i][j] = max(LCS[i - 1][j], LCS[i][j - 1])여기서 살펴봐야 될 것은 else 구문입니다.
LCS[i - 1][j]와 LCS[i][j - 1]의 의미
여기서 기본적으로 생각하고 가야될 것이 있습니다.
❗ i와 j는 두 String의 Index 값
부분 수열은 연속된 값이 아닙니다. 때문에 현재의 문자를 비교하는 과정 이전의 최대 공통 부분수열은 계속해서 유지됩니다. '현재의 문자를 비교하는 과정' 이전의 과정이 바로 LCS[i -1]과 LCS[i][j - 1]이 됩니다.
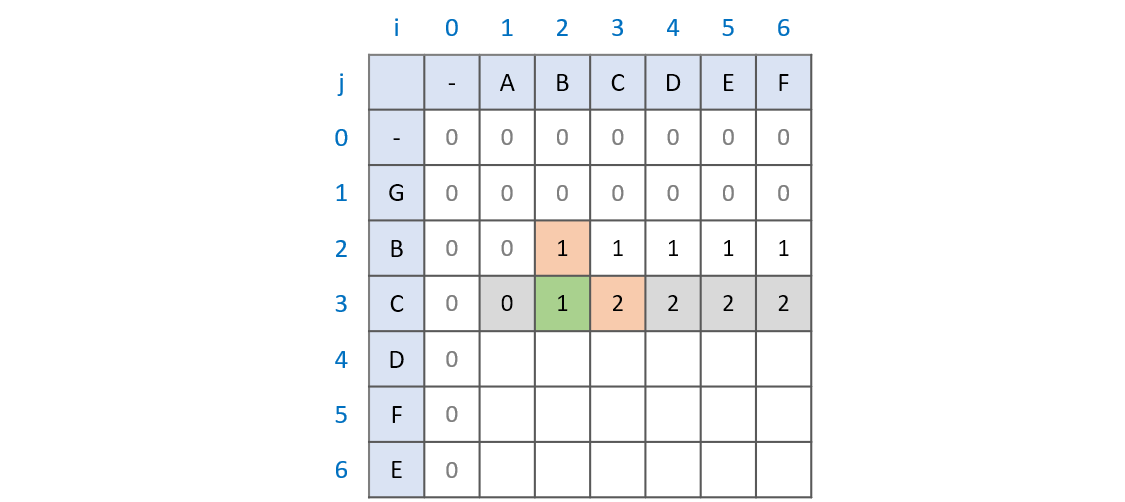
문자열 AB와 GBC를 비교(위 그림의 초록색 부분)하는 과정을 예로 들어보겠습니다. AB와 GBC의 최대 공통 부분수열이 B라는 것을 알기 위해서는 문자열 A와 GBC를 비교하는 과정, 문자열 AB와 GB를 비교하는 과정이 필요합니다. 문자열 AB와 GB의 비교 과정에서 최대 공통 부분수열이 B임을 확인했기 때문에 문자열 AB와 GBC의 최대 공통 부분수열 역시 B가 되는 것입니다.

왜 문자가 같으면 LCS[i][j] = LCS[i - 1][j - 1] + 1인가?
최대 공통 문자열을 구할 때 비교하는 문자가 같으면 LCS[i][j] = LCS[i - 1][j - 1] + 1의 과정을 거쳤습니다. 이 과정이 어떻게 최대 공통 부분수열에도 똑같이 적용될수 있을까?
부분수열은 연속할 필요가 없음을 위에서 확인했습니다. 두 문자가 같은 상황이 오면 지금까지의 최대 공통 부분수열에 1을 더해주는 것입니다.
즉, i와 j의 인덱스 이후에 모두 1씩 더해주는 것입니다.
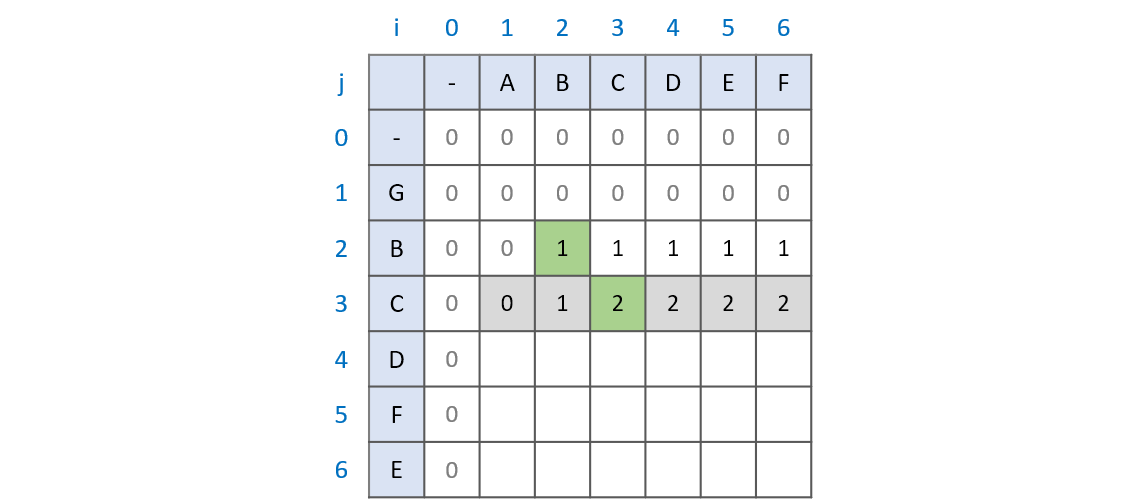
문자열 ABC와 GBC를 비교(초록색 부분)하는 과정을 예로 들어보겠습니다. LCS 배열은 LCS[i - 1][j]와 LCS[i][j - 1]의 비교를 통해 언제나 본인까지의 최대 공통 부분수열 값을 가지고 있습니다. 문자열 AB와 GB를 비교할 때와 문자열 ABC와 GBC를 비교할 때 달라진 점은 두 문자열 모두에 C가 추가된 점입니다. 때문에 기존으 ㅣ최대 공통 부분수열인 B와 C를 더한 BC가 최대 공통 부분수열이 되는 것입니다.

코드
JAVA 코드의 경우 다음과 같습니다.
void lcs_dp(int[][] dp, String str1, String str2, int str1Len, int str2Len) {
for (int i = 1; i < str1Len + 1; i++) {
for (int j = 1; j < str2Len + 1; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
}구현 과정
구현 과정은 다음과 같습니다.
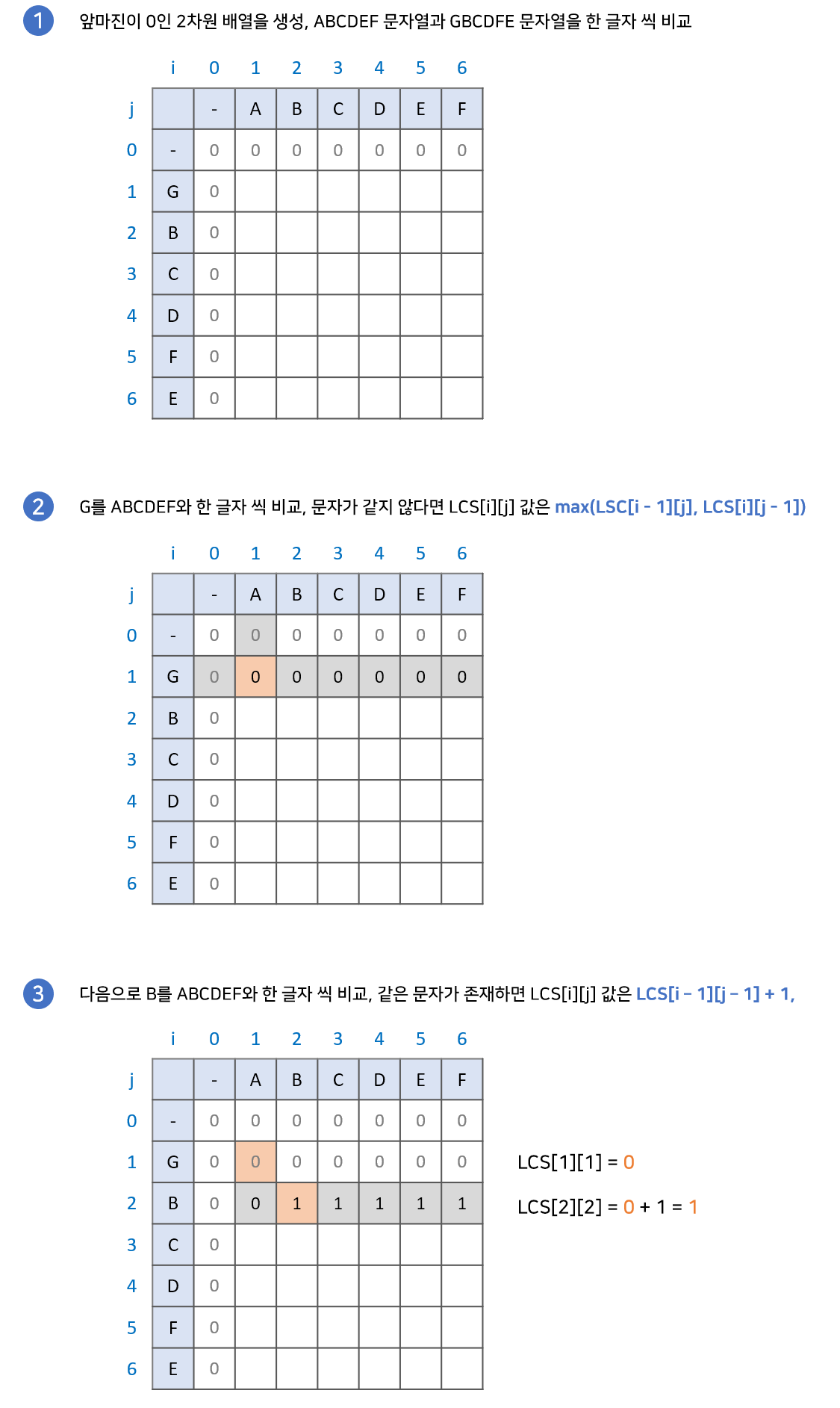
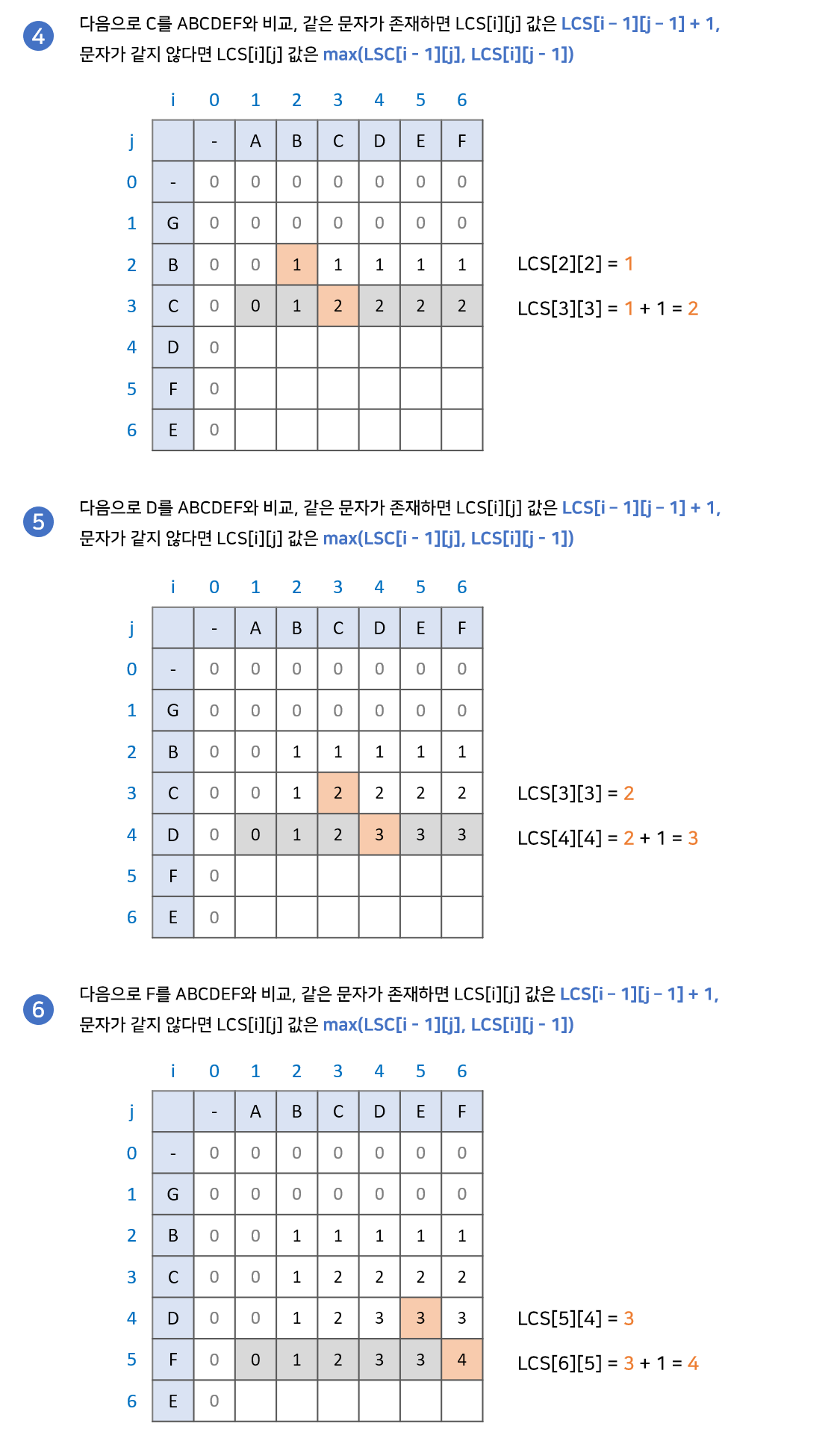

최장 공통 부분수열 문자열 찾기
위에서 LCS 구현 과정을 통해 최장 공통 부분 수열의 길이를 알아봤습니다.
그렇다면, 해당 수열의 문자열은 어떻게 될까요?
과정은 다음과 같습니다.
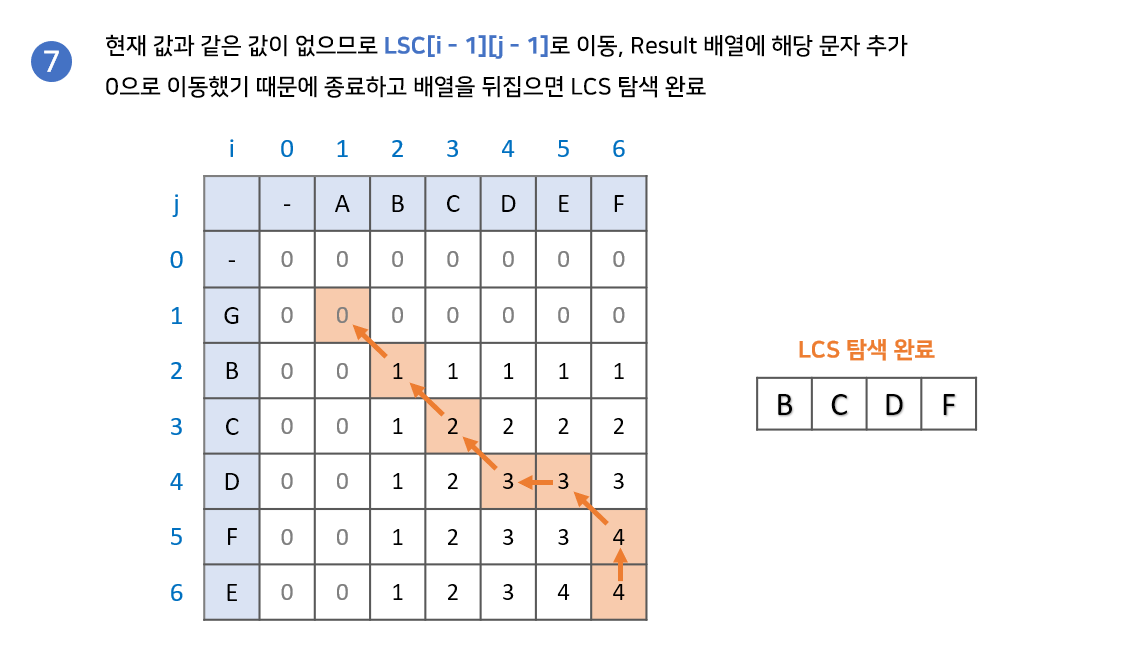
- LCS 배열의 가장 마지막 값에서 시작합니다. 결과값을 저장할 result배열을 준비합니다.
LCS[i - 1][j]와LCS[i][j - 1]중 현재 값과 같은 값을 찾습니다.
2.1. 만약 같은 값이 있다면 해당 값으로 이동
2.2. 만약 같은 값이 없다면result배열에 해당 문자를 넣고LCS[i - 1][j - 1]로 이동- 2번 과정을 반복하다가 0으로 이동하게 되면 종료.
result배열의 역순이 LCS 입니다.
구현 과정
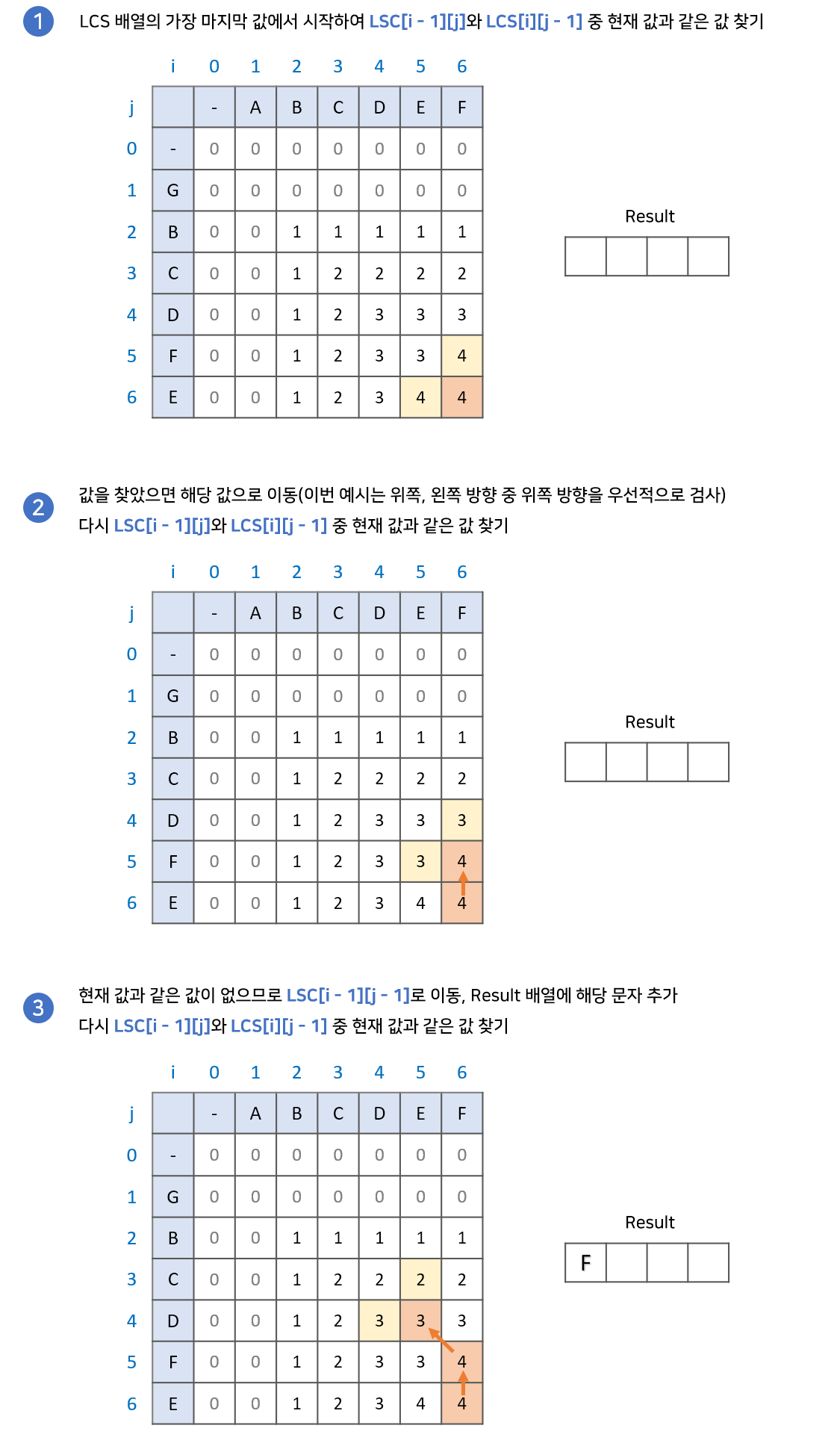
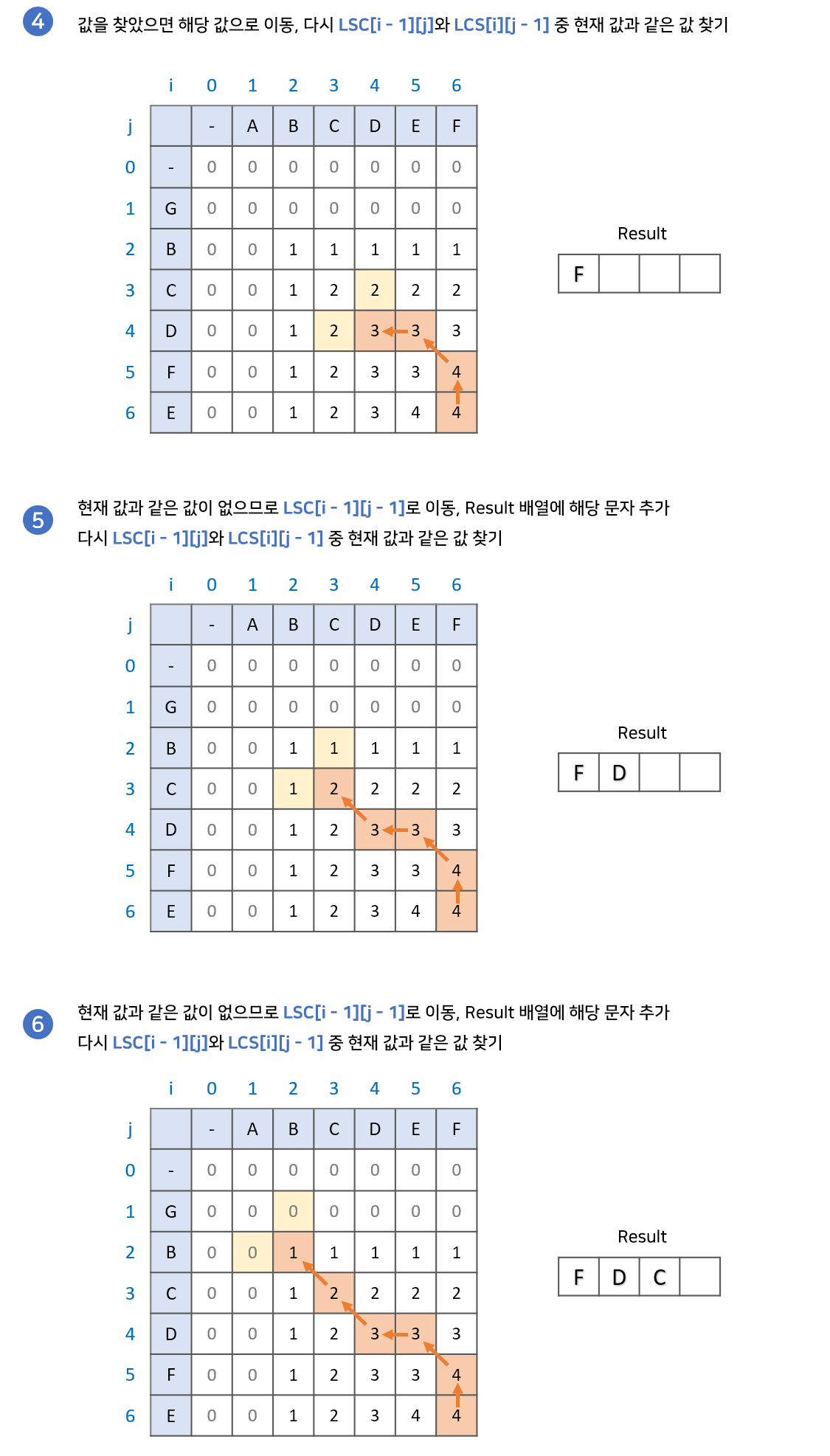
Reference
