백준 17825번: 주사위 윷놀이 복습하는 도중에 문득 내가 순열과 조합에 대해서 재대로 알고 있는 것이 맞는지 의문이 들었습니다.
이번 블로그 정리의 목적은 간단한 개념 정리 및 코드 구현이 아닌 좀 더 심화된 내용을 다뤄볼까 합니다.
따라서 순열과 조합이 무엇인지 간단히 정리하고 코드로 구현해보고 넘어가겠습니다.
일단 순열과 조합 둘 다 기본적으로 중첩 반복문과 재귀 함수의 형태로 표현이 가능합니다.
이 둘에 대해서 알아보기 전에 팩토리얼을 알아야 수식 표현이 간단해 지니깐 정리하고 가겠습니다.
팩토리얼
❗️ 팩토리얼(factorial)은 n이 자연수일 때, 1 부터 n 까지의 모든 자연수의 곱을 의미합니다.
따라서, 이와 같은 형태로 표현이 가능합니다.
n! = n * (n - 1) * (n - 2) * ...*1순열(nPr)
❗️ 순열(Permutation)이란 순서대로 뽑아서 줄을 세우는 걸 의미합니다.
여기서 nPr이 의미하는 것은 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다.
이것을 코드로 구현하는 것은 다음과 같습니다.
중첩 반복문(중복 사용 불가)
int[] nums = {1, 3, 5};
List<Integer[]> result = new ArrayList<>();
int size = nums.length;
boolean[] isUsingNum = new boolean[size];
Integer[] buffer = new Integer[size];
int ptr = 0;
for (int i = 0; i < size; i++) {
if (!isUsingNum[i]) {
buffer[ptr++] = nums[i];
isUsingNum[i] = true;
for (int j = 0; j < size; j++) {
if (!isUsingNum[j]) {
buffer[ptr++] = nums[j];
isUsingNum[j] = true;
for (int k = 0; k < size; k++) {
if (!isUsingNum[k]) {
buffer[ptr++] = nums[k];
result.add(Arrays.copyOf(buffer, size));
buffer[--ptr] = 0;
}
}
buffer[--ptr] = 0;
isUsingNum[j] = false;
}
}
buffer[--ptr] = 0;
isUsingNum[i] = false;
}
}원소 3개만을 사용했는데, 너무 복잡하다. 중첩 반복문은 사실상 사용할 수 있는 코드가 아니라고 봅니다.
재귀함수는 다음과 같은 형태로 되어있습니다.
private static void recursive(List<Integer[]> result, int[] nums, int ptr, Integer[] buffer, int size, boolean[] isUsingNum) {
if (ptr == size) {
result.add(Arrays.copyOf(buffer, size));
} else {
for (int i = 0; i < nums.length; i++) {
if (!isUsingNum[i]) {
buffer[ptr] = nums[i];
isUsingNum[i] = true;
recursive(result, nums, ptr + 1, buffer, size, isUsingNum);
isUsingNum[i] = false;
buffer[ptr] = 0; // 이 부분은 생략 가능하지만 저같은 경우에는 처리를 해주는 것이 좀 더 직관적으로 느껴져서 작성합니다.
}
}
}
}물론, 해당 코드를 그대로 사용하는 상황은 그다지 많지 않을 것입니다. 순열 자체가 상당히 높은 경우의 수를 뽑아내기 때문에 보통은 조건을 걸어두고 backtracking으로 구현하게 될 가능성이 클 것이라고 판단하지만, 그것 또한 해당 코드 방식인 재귀 함수에서 확장되는 방식이라고 판단합니다.
조합(nCr)
조합(Combination)이란 유한 개의 원소에서 주어진 수만큼의 원소들을 고르는 방법입니다.
여기서 nCr이 의미하는 것은 서로 다른 n개중에 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 없음)
조합의 경우에도 중첩 반복문을 사용해서 구현가능 합니다.
의 경우 다음과 같습니다.
int[] nums = {1, 3, 5, 8, 9};
List<Integer[]> result = new ArrayList<>();
int size = nums.length;
final int MAX_BUFFER_SIZE = 3;
Integer[] buffer = new Integer[MAX_BUFFER_SIZE];
int bufferSize = 0;
for (int i = 0; i < size - 2; i++) {
buffer[bufferSize++] = nums[i];
for (int j = i + 1; j < size - 1; j++) {
buffer[bufferSize++] = nums[j];
for (int k = j + 1; k < size; k++) {
buffer[bufferSize] = nums[k];
result.add(Arrays.copyOf(buffer, MAX_BUFFER_SIZE));
buffer[bufferSize] = 0;
}
buffer[--bufferSize] = 0;
}
buffer[--bufferSize] = 0;
}해당 코드 역시 좋아보이진 않습니다.
조합도 재귀 함수로 표현이 가능한데 같은 상황에서 재귀함수 방식을 사용할 경우 다음과 같습니다.
private static void recursive(List<Integer[]> result, Integer[] buffer, int[] nums, int ptr, int size, int bufferSize, int MAX_BUFFER_SIZE) {
if (bufferSize == MAX_BUFFER_SIZE) {
result.add(Arrays.copyOf(buffer, MAX_BUFFER_SIZE));
} else if (ptr < size) {
buffer[bufferSize] = nums[ptr];
recursive(result, buffer, nums, ptr + 1, size, bufferSize + 1, MAX_BUFFER_SIZE);
buffer[bufferSize] = 0;
recursive(result, buffer, nums, ptr + 1, size, bufferSize, MAX_BUFFER_SIZE);
}
}📌 여기서 Tip
해당 방식을 말로 표현해보자면 순서랑 상관이 없으니 정렬을 하던 안하던 상관없이 list들을 순차적으로 탐색하면서 원소를 뽑고, 안뽑고를 결정하면서 넘어가는 것입니다. 그러다가 buffer의 크기가 다 찼다면 다 선택한 것이니깐 결과에 넣어주고 다시 돌아간다면 뽑는 경우가 아닌 안뽑는 경우가 실행될 것이고 이것이 반복적으로 수행될 것입니다. (backtracking)
조합은 또 한 가지 방법을 더 사용할 수 있습니다.
bitmasking 기법을 사용하는 것인데 다음과 같습니다.
int[] nums = {1, 3, 5, 8, 9};
List<Integer[]> result = new ArrayList<>();
int size = nums.length;
final int MAX_BUFFER_SIZE = 3;
Integer[] buffer = new Integer[MAX_BUFFER_SIZE];
for (int i = (1 << 3) - 1; i < (1 << size); i++) {
if (Integer.bitCount(i) == 3) {
int bufferSize = 0;
for (int j = 0; j < size; j++) {
if ((i & (1 << j)) != 0) {
buffer[bufferSize++] = nums[j];
}
}
result.add(Arrays.copyOf(buffer, MAX_BUFFER_SIZE));
}
} 개인적으로는 해당 코드도 굉장히 좋아하는 편입니다.
좀 더 복잡한 경우
여기서부터는 기본적인 순열, 조합 방식이 아닌 좀 더 복잡한 상황에 대해서 정리를 해보려고 합니다.
중복 순열은 사실상 isUsingNum만 사용하지 않는다면 간단하게 구현되는 문제라 넘어가겠습니다.
중복 순열의 공식은 다음과 같습니다.
중복 조합의 경우에는 어떻게 구현해야 할까요?
중복 조합
중복 조합이란 중복 가능한 n개중에서 r개를 선택하는 경우의 수를 의미합니다. (순서 상관 없음)
공식은 다음과 같습니다.
코드로는 다음과 같이 구현할 수 있습니다.
private static void backTracking(List<Integer[]> result, Integer[] buffer, int[] nums, int size, int ptr, int bufferSize, int MAX_BUFFER_SIZE) {
if (bufferSize == MAX_BUFFER_SIZE) {
result.add(Arrays.copyOf(buffer, bufferSize));
} else if (ptr < size) {
// 원소를 넣어주는 경우에도 ptr이 증가하지 않습니다.
buffer[bufferSize] = nums[ptr];
backTracking(result, buffer, nums, size, ptr, bufferSize + 1, MAX_BUFFER_SIZE);
buffer[bufferSize] = 0;
backTracking(result, buffer, nums, size, ptr + 1, bufferSize, MAX_BUFFER_SIZE);
}
}같은 것이 있는 순열
순열이 같은 것이 포함된 원소들을 나열하는 경우의 수는 나열하는 원소의 팩토리얼에 중복된 원소들의 팩토리얼을 나누어주면 됩니다.
예를 들어 aaabb와 같은 경우 a가 3개이고 b가 2개이므로 5!을 3!와 2!로 나누어주면 됩니다.
이와 같은 형태로 구현이 되고 그렇다면 코드는 어떻게 구현이 될까요?
private static void permuteUnique(int[] nums, List<Integer[]> result, int size) {
Arrays.sort(nums);
backTracking(result, new Integer[size], nums, new boolean[size], 0, size);
}
private static void backTracking(List<Integer[]> result, Integer[] buffer, int[] nums, boolean[] isUsingNum, int ptr, int size) {
if (size == ptr) {
result.add(Arrays.copyOf(buffer, size));
} else if (ptr < size) {
for (int i = 0; i < size; i++) {
if (isUsingNum[i] || (i > 0 && nums[i] == nums[i - 1] && !isUsingNum[i - 1])) continue;
buffer[ptr] = nums[i];
isUsingNum[i] = true;
backTracking(result, buffer, nums, isUsingNum, ptr + 1, size);
isUsingNum[i] = false;
buffer[ptr] = 0;
}
}
}중요한 점은 다음과 같습니다.
- 정렬을 해서 같은 원소끼리 붙여둡니다.
- 같은 원소가 여러 개일 경우에는 앞의 원소를 먼저 사용해야만 뒤의 원소를 사용할 수 있도록 설정해서 중복을 피합니다.
원 순열
원 순열은 원 모양의 테이블에 n개의 원소를 나열하는 하는 경우의 수입니다.
공식은 다음과 같습니다.
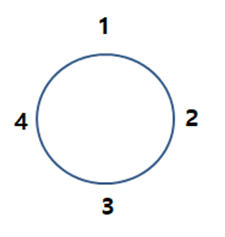
예를 들어 원 모양의 테이블에 4명을 앉힐려고 한다면
1에서 시작해서 1234로 앉히던
2에서 시작해서 2341로 앉히던
3에서 시작해서 3412로 앉히던
4에서 시작해서 4123로 앉히던
원을 돌리면 모두 같다고 봅니다.
이것을 코드로 표현하자면 어떻게 할까요?
핵심은 숫자 하나를 고정해놓고 나머지 숫자들을 정렬하는 것입니다.
숫자 하나를 고정함으로써 나머지 숫자들을 정렬하는 것은 일반 순열 방식과 동일합니다. 따라서, 일반 순열을 구현하는 부분에서 첫번째 요소를 고정해놓고 ptr을 1부터 탐색하기 시작하면 문제 없이 구현할 수 있습니다.
염주 순열
이 경우는 원 순열에서 추가되는 것이 뒤집힌 숫자도 동일하다고 판단하는 조건이 추가됩니다.
n개의 서로 다른 종류의 구슬로 목걸이를 만드는 경우의 수
코드는 다음과 같습니다.
private static void recursive(List<Integer[]> result, TreeSet<String> set, Integer[] buffer, int[] nums, boolean[] isUsingNum, int ptr, int size) {
if (ptr == size) {
String strValue = arrayToString(buffer);
String reverseStrValue = (new StringBuffer(strValue)).reverse().toString();
if (set.contains(strValue) || set.contains(reverseStrValue)) return;
result.add(Arrays.copyOf(buffer, size - 1));
set.add(strValue);
set.add(reverseStrValue);
} else {
for (int i = 1; i < size; i++) {
if (!isUsingNum[i]) {
buffer[ptr - 1] = nums[i];
isUsingNum[i] = true;
recursive(result, set, buffer, nums, isUsingNum, ptr + 1, size);
buffer[ptr - 1] = 0;
isUsingNum[i] = false;
}
}
}
}
private static String arrayToString(Integer[] nums) {
StringBuilder sb = new StringBuilder();
for (int num : nums) {
sb.append(num);
}
return sb.toString();
}
private static void printResult(List<Integer[]> result, int fixNum) {
for (Integer[] value : result) {
System.out.print(fixNum + " ");
for (int i : value) {
System.out.print(i + " ");
}
System.out.println();
}
}조금 더 복잡해 졌는데, 핵심은 Set을 이용하여 표준 형태와 뒤집은 형태를 기록해두고 확인하는 방식으로 구현합니다.
집합의 분할
집합의 분할이란 서로 다른 n개를 똑같은 상자 k개에 넣는 경우의 수를 의미합니다. (빈상자는 있으면 안됌)]
예를 들어서, 서로 다른 6개의 공을 똑같이 생긴 2개의 상자에 넣는 경우의 수같은 상황을 의미합니다.
현재, 필자가 위에서 언급했었던 백준 17825번: 주사위 윷놀이 문제도 이 방식을 요구합니다. "순서가 정해져있는" 주사위 숫자들을 똑같은 말 4개에게 할당해주는 방식을 요구합니다. 물론, 같은 칸에 겹치면 안되는 추가적인 조건이 존재하지만 기본적인 방식은 해당 방식과 동일할 것입니다.
순서가 정해져 있기 때문에 같은 숫자라도 1번째의 숫자 1과 3번째의 숫자 1은 다른 의미를 가지게 되기 때문에 모든 숫자가 다르다고 판단할 수 있을 것 같습니다.
다만, 둘의 차이점은 백준 문제의 경우 말을 사용하지 않아도 되긴 때문에 빈 공집합이 허용되지만 일반적인 집합의 분할에서는 공집합이 허용되지 않습니다.
공식은 다음과 같습니다.
ex) 서로 다른 6개의 공을 똑같이 생긴 2개의 상자에 넣는 경우의 수
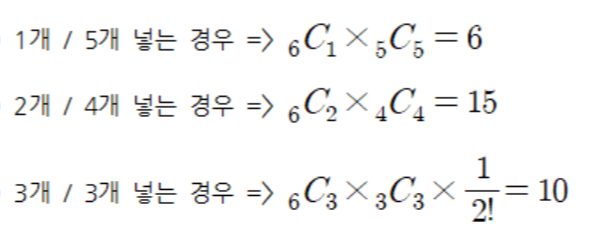
공집합이 허용되지 않는 코드의 경우 다음과 같습니다.
int[] nums = {1, 2, 3, 4, 5};
int n = nums.length;
int k = 3;
List<List<Integer>[]> result = new ArrayList<>();
List<Integer>[] partitions = initPartitionsTable(n);
backtrakcing(result, partitions, nums, 0, n, k);
printResult(result, k);
}
private static void backtrakcing(List<List<Integer>[]> result, List<Integer>[] partitions, int[] nums, int ptr, int size, int k) {
if (ptr == size) {
if (allPartitionsUsed(partitions, k)) {
result.add(copyPartitionsReuslt(partitions, k));
}
} else {
for (int i = 0; i < k; i++) {
if (!partitions[i].isEmpty() || (i == 0 || !partitions[i - 1].isEmpty())) {
partitions[i].add(nums[ptr]);
backtrakcing(result, partitions, nums, ptr + 1, size, k);
partitions[i].remove(partitions[i].size() - 1);
}
}
}
}
private static boolean allPartitionsUsed(List<Integer>[] partitions, int k) {
for (int i = 0; i < k; i++) {
if (partitions[i].isEmpty()) return false;
}
return true;
}
private static List<Integer>[] copyPartitionsReuslt(List<Integer>[] partitions, int k) {
List<Integer>[] copy = initPartitionsTable(k);
for (int i = 0; i < k; i++) {
for (int j = 0; j < partitions[i].size(); j++) {
copy[i].add(partitions[i].get(j));
}
}
return copy;
}
private static List<Integer>[] initPartitionsTable(int k) {
List<Integer>[] partitions = new List[k];
for (int i = 0; i < k; i++) {
partitions[i] = new ArrayList<>();
}
return partitions;
}핵심은 요소 하나씩 탐색하면서 뒤의 박스를 사용하려면 앞의 박스 사용을 강제하도록 하는 것입니다.
백준 문제의 경우 빈 말의 사용이 가능했었죠? 그렇다면 allPartitionsUsed() 함수를 사용하지 않는다면 됩니다. 다른 조건들이 있으니 그것에 맞춰서 풀어주면 될 것입니다.
추가적으로 k가 2인 경우에 한해서 비트 마스킹 풀이도 가능합니다.
int[] nums = {1, 2, 3, 4, 5, 6};
List<List<Integer>> groupAList = new ArrayList<>();
List<List<Integer>> groupBList = new ArrayList<>();
int size = nums.length;
for (int i = (1 << (size - 1)); i < (1 << size); i++) {
List<Integer> groupA = new ArrayList<>();
List<Integer> groupB = new ArrayList<>();
for (int j = 0; j < size; j++) {
if ((i & (1 << j)) != 0) {
groupA.add(nums[j]);
} else {
groupB.add(nums[j]);
}
}
if (groupA.isEmpty() || groupB.isEmpty()) continue;
groupAList.add(groupA);
groupBList.add(groupB);
}자연수 분할과, 이항 정리는 굳이 정리할 필요가 있을 것 같지 않아서 여기까지 정리하고 마무리 하겠습니다.
