세그먼트 트리
세그먼트 트리를 배우기 앞서..
먼저 세그먼트 트리가 무엇인지 알아보기 앞서 해당 문제를 살펴봅시다.
문제
크기가 N인 정수 배열 A가 있고, 여기서 다음과 같은 연산을 최대 M번 수행해야 하는 문제가 있습니다.
- 구간 l, r(l ≤ r)이 주어졌을 때, A[l] + A[l + 1] + … + A[r - 1] + A[r]을 구해서 출력하기
- i번째 수를 v로 바꾸기 (A[i] = v)
1번 연산 A[l] + A[l + 1] + … + A[r - 1] + A[r]을 구하기 위해 소스 1과 같이 모두 더하는 방법이 있습니다.
int ans = 0;
for (int i = l; i <= r; i++) {
ans += a[i];
}해당 코드의 시간 복잡도는 O(N)입니다. 2번 연산 A[i] = v는 O(1)입니다. 연산을 최대 M번 수행해야 하니 연산 하나의 시간 복잡도는 O(N)입니다. 총 시간 복잡도는 O(NM)입니다.
누적 합
누적 합을 사용하면, 1번 연산의 시간 복잡도를 O(1)로 줄일 수 있습니다. 하지만, 2번 연산으로 수가 변경될 때마다 누적 합을 다시 구해야 하기 때문에, 2번 연산의 시간 복잡도는 O(N)입니다. 연산 하나의 시간 복잡도는 O(N)이니 총 시간 복잡도는 O(NM)이 됩니다.
누적 합은 해당 페이지를 참고하면 될 것 같습니다.
세그먼트 트리를 사용하면 해당 연산들의 시간 복잡도를 줄일 수 있습니다.
이제 본격적으로 세그먼트 트리(Segment Tree)에 대해서 알아보도록 하겠습니다.
세그먼트 트리(Segment Tree)
세그먼트 트리를 사용하면 1번 연산과 2번 연산을 O(logN)에 수행할 수 있습니다.
세그먼트 트리의 리프 노드와 리프 노드가 아닌 다음과 같은 의미를 가집니다.
- 리프 노드: 배열의 그 수 자체
- 리프 노드가 아닌 노드: 왼쪽 자식과 오른쪽 자식의 합을 저장
어떤 노드의 번호가 x일때, 왼쪽 자식의 번호는 2x, 오른쪽 자식의 번호는 2x + 1이 됩니다.
구현 방식
-
리프 노드를 제외한 다른 모든 노드는 항상 2개의 자식을 가집니다.
- 따라서, 세그먼트 트리는 Full Binary Tree의 형태를 가집니다.
- 만약, N이 2의 제곱꼴인 경우에는 Perfect Binary Tree가 됩니다.
-
리프 노드가 N개인 Full Binary Tree에는 리프 노드가 아닌 노드가 N - 1개 있습니다. 따라서, 필요한 노드의 수는 2N - 1개 있습니다.
참고로 필요한 노드의 수랑 배열의 크기랑은 별개임을 주의합시다.
-> 세그 먼트 트리의 경우 Full Binary Tree인데, 완전 이진 트리가 아니기 때문에 배열의 순서대로 노드가 채워지는 것이 아니다.- N이 2의 제곱꼴이 아닌 경우에 높이 h = logN입니다.
-
세그먼트 트리(Segment Tree)의 정보를 저장하기 위해서 배열을 사용하겠습니다. 깊이가 가장 깊은 노드와 가장 깊지 않은 리프 노드의깊이 차이는 1보다 작거나 같습니다. 따라서, 배열을 이용해도 공간을 크게 낭비하지 않습니다.
- tree[x] 에 노드 x의 정보를 저장
Size 구하는 방법
=> 먼저 h를 구하고 tree_size를 결정하면 됩니다.int h = (int)Math.ceil(Math.log(n) / Math.log(2)); int tree_size = 1 << (h + 1);
// a: 배열 A
// tree: 세그먼트 트리
// node: 노드 번호
// node에 저장되어 있는 합의 범위가 start - end
void init(long[] a, long[] tree, int node, int start, int end) {
if (start == end) {
tree[node] = a[start];
} else {
init(a, tree, node*2, start, (start+end)/2);
init(a, tree, node*2+1, (start+end)/2+1, end);
tree[node] = tree[node*2] + tree[node*2+1];
}
}코드에 대해서 좀 더 설명하자면 다음과 같습니다.
start == end인 경우는 리프 노드의 경우입니다. 리프 노드는 배열의 그 수를 저장해야 하기 때문에, tree[node] = a[start]가 됩니다.
node의 왼쪽 자식은 node*2이고, 오른쪽 자식은 node*2 + 1입니다. 또, node에 저장된 구간이[start,end]라면, 왼쪽 자식은 [start, (start + end) / 2], 오른쪽 자식은 [(start + end) / 2 + 1, end]가 저장된 구간입니다.
tree[node]에 저장될 값을 구하려면 왼쪽 자식에 저장된 값 tree[node*2], 오른쪽 자식에 저장된 값 tree[node * 2 + 1]을 먼저 구해야 합니다. 따라서, 재귀 함수를 이용해 각각의 값을 먼저 구했습니다.
구간의 합 구하기
구간 left, right가 주어졌을 때, 합을 구하려면 트리를 순회하면서 각 노드에 저장된 구간의 정보와 left, right와의 관계를 살펴봐야 합니다.
node에 저장된 구간이 [start, end] 이고, 합을 구해야하는 구간이 [left, right] 라면 다음과 같이 4가지 경우로 나누어질 수 있습니다.
- [left, right]와 [start, end]가 겹치지 않는 경우
- [left, right]가 [start, end]를 완전히 포함하는 경우
- [start, end]가 [left, right]를 완전히 포함하는 경우
- [left, right]와 [start, end]가 겹쳐져 있는 경우(1, 2, 3 제외한 나머지 경우)
1번의 경우에는 if (left > end || right < start)로 나타낼 수 있습니다. left > end는 [start, end] 뒤에 [left, right]가 있는 경우이고, right < start는 [start, end]앞에 [left, right]가 있는 경우입니다. 이 경우에는 겹치지 않기 때문에, 더이상 탐색을 이어나갈 필요가 없습니다. 따라서 0을 리턴해 탐색을 종료합니다.
2번의 경우는 if (left ≤ start && end ≤ right)로 나타낼 수 있습니다. 이 경우도 더 이상 탐색을 이어나갈 필요가 없습니다. 구해야하는 합의 범위는 [left, right]인데, [start, end]는 그 범위에 모두 포함되고, 그 node의 자식도 모두 포함되기 때문에 더이상 호출을 하는 것은 비효율적입니다. 따라서, tree[node]를 리턴해 탐색을 종료합니다.
3번과 4번의 경우에는 왼쪽 자식과 오른쪽 자식을 루트로 하는 트리에서 다시 탐색을 시작해야 합니다.
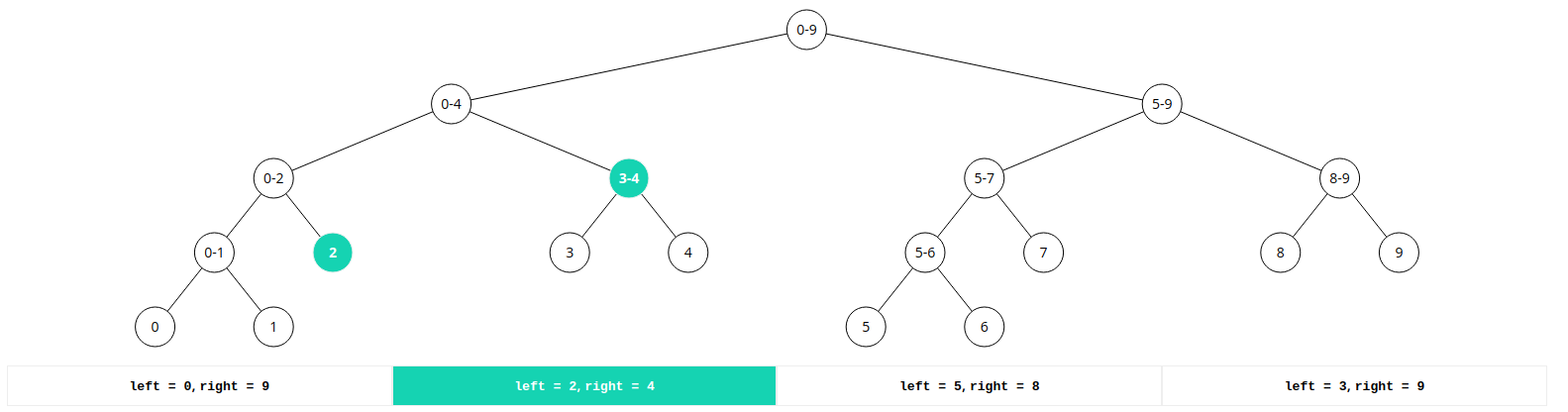
예를 들어 이와 같은 경우를 보자.
left = 0, right = 9인 경우에는 맨 위의 루트 노드만으로 바로 합을 알 수 있습니다.
하지만, left = 2, right = 4인 경우에는 다음과 같이 구해질 것입니다.
먼저, 루트 노드에서 재귀 함수의 형태로 탐색을 들어갈 것이고 왼쪽 오른쪽 탐색이 들어갈 것입니다. 여기서 오른쪽 탐색은 1번의 경우로서 겹치는 부분이 없어서 탐색을 종료합니다.
0 - 9에서 왼쪽으로 탐색이 들어가고 0 - 4로 갈 것입니다. 구하려는 합의 범위가 2 - 4이기 때문에, 0 - 4가 더 큰 범위라서 나눠져서 들어가야 합니다.(3번의 경우)
그래서 왼쪽 오른쪽으로 다시 탐색이 들어갈 것이고, 이와 같은 방식으로 2 , 3 - 4의합을 찾아내서 그 둘을 더해서 구간의 합을 구할 것입니다. 여기서 5 - 9는 1번의 경우로서 겹치지 않기 때문에 탐색을 종료합니다.
left = 3, right = 9인 경우에 조금만 살펴보자면 위와 같은 방식으로 루트 노드에서 왼쪽 서브 트리와 오른쪽 서브 트리로 탐색이 이루어질 것입니다. 여기서 주목해야 할 점은 오른쪽 서브트리입니다.
5 - 9의 경우에는 3 - 9에 포함되어 있기 때문에 결국 더이상의 탐색이 불필요합니다. 이미 구하려는 범위의 합에 포함되어 있기 때문입니다.(2번의 경우)
최종적으로는 왼쪽 서브 트리에서 3 - 4, 오른쪽 서브 트리에서 5 - 9를 꺼내와서 둘의 합을 구하면서 종료할 것입니다.
코드는 다음과 같습니다.
long query(long[] tree, int node, int start, int end, int left, int right) {
if (left > end || right < start) {
return 0;
}
if (left <= start && end <= right) {
return tree[node];
}
long lsum = query(tree, node*2, start, (start+end)/2, left, right);
long rsum = query(tree, node*2+1, (start+end)/2+1, end, left, right);
return lsum+rsum;
}수 변경하기
index번째 수를 val로 변경하는 경우, index번째를 포함하는 노드에 들어있는 합만 변경해주면 됩니다.
원래 index번째 수가 a[index]였고, 바뀐 수가 val이라면, 합은 val - a[index]만큼 변합니다.
수 변경은 다음과 같이 2가지 경우가 있습니다.
- [start, end]에 index가 포함되는 경우
- [start, end]에 index가 포함되지 않는 경우
1번 경우에만 재귀 호출을 진행하고, 2번의 경우는 그 노드의 모든 자식도 index번째를 포함하지 않으니 재귀 호출을 중단하면 됩니다.
리프 노드를 찾으면 그 노드의 합을 변경해줍니다. 이후 리턴될 때마다 각 노드의 합을 자식에 저장된 합을 이용해 다시 구하면 됩니다.
void update(long[] a, long[] tree, int node, int start, int end, int index, long val) {
if (index < start || index > end) {
return;
}
if (start == end) {
a[index] = val;
tree[node] = val;
return;
}
update(a, tree,node*2, start, (start+end)/2, index, val);
update(a, tree,node*2+1, (start+end)/2+1, end, index, val);
tree[node] = tree[node*2] + tree[node*2+1];
}이 방식 말고도 다른 방법도 있습니다. 해당 방식은 vector을 이용하는 방법인데 필자가 벡터에 대해서 정확한 이해도가 없기 때문에 추후에 공부하고 내용을 추가할 예정입니다.
update(a, tree, index, val)은 index번째를 val로 변경하는 코드이고, 이 함수는 index번째를 포함하는 모든 노드의 합에 diff를 더해서 수를 변경하는 update_tree(tree, node, start, end, index, diff)를 호출하는 소스입니다.
void update_tree(vector<long long> &tree, int node, int start, int end, int index, long long diff) {
if (index < start || index > end) return;
tree[node] = tree[node] + diff;
if (start != end) {
update_tree(tree,node*2, start, (start+end)/2, index, diff);
update_tree(tree,node*2+1, (start+end)/2+1, end, index, diff);
}
}
void update(vector<long long> &a, vector<long long> &tree, int n, int index, long long val) {
long long diff = val - a[index];
a[index] = val;
update_tree(tree, 1, 0, n-1, index, diff);
}시간 복잡도
구간의 합 구하기
트리의 각 레벨에서 방문하는 노드의 개수는 4개를 넘지 않습니다. 트리의 높이 H는 logN이기 때문에, 합을 구하는 시간 복잡도는 logN입니다.
첫번째 레벨에서는 루트 노드 하나만 있고, 루트 노드는 반드시 방문하게 됩니다.
리프 노드가 아닌 노드는 2개의 자식을 갖고, 재귀 호출을 하는 경우 항상 2개의 호출을 하게 됩니다. 어떤 레벨에서 방문한 노드의 개수가 2개 이하인 경우에는 다음 레벨에서 방문한 노드의 개수는 4개 이하입니다.
어떤 레벨에서 방문한 노드의 수가 3개 또는 4개인 경우에 다음 레벨에서 방문한 노드의 수가 4개 이하인지 살펴보면 됩니다.
사실 이부분은 무슨 말인가 싶기도 했습니다. 다음 페이지에서 소스 3에서 예제를 입력해보면서 동작하는 방식을 확인해보는 것이 있으니 참고바랍니다.
레벨 l에서 방문한 노드가 3개이고, l, m, r이라고 해봅시다. m은 절대로 재귀 호출을 하지 않습니다. 세그먼트 트리의 모든 퀴리는 연속된 구간의 합을 구하게 되는데, m은 항상 부모 노드의 구간에 포함되는 노드입니다. 재귀 호출이 일어났다는 것은 그 구간의 일부만 포함되어야 한다는 것을 의미하기 때문입니다. 방문한 노드가 4개인 경우도 가장 왼쪽과 오른쪽에 있는 재귀 호출을 할 수 있고, 가운데 있는 노드는 재귀 호출을 하지 않습니다.
따라서, 각 레벨에서 최대 4개의 노드만 방문할 수 있습니다.
수 변경하기
트리의 각 레벨에서 방문하는 노드의 개수는 2개를 넘지 않습니다. 트리의 높이 H는 logN이기 때문에, 시간 복잡도는 logN입니다.
세그먼트 트리를 이용해서 구간의 최솟값도 구할 수 있습니다. 최솟값 이외에도 최댓값, 곱, XOR 연산 등도 구할 수 있습니다.
Reference
