[Java] 보이어-모어(Boyer-Moore)

서정범·2023년 3월 13일
algorithmstring search()
0

자료구조와 알고리즘

목록 보기
22/30
post-custom-banner

Boyer-Moore법

Boyer-Moore법이란?

Boyer-Moore법은 브루트-포스법을 개선한 KMP법보다 효율이 더 우수하기 때문에 실제로 문자열 검색에서 널리 사용하는 알고리즘입니다.

이 알고리즘은 패턴의 마지막 문자부터 앞쪽으로 검사를 진행하면서 일치하지 않은 문자가 있으면 미리 준비한 표에 따라 패턴을 옮길 크기를 정합니다.

기본적으로 Boyer-Moore법은 두 접근 방식의 결합이다.

  1. Bad Character Heuristic(나쁜 문자 이동)
  2. Good Suffix Heuristic(착한 접미부 이동)

위 두 방법은 텍스트에서 패턴을 찾는데 있어 독립적으로 사용 될 수 있다.

사실, 필자가 보고 공부하는 책(Do it! 자료구조와 함께 배우는 알고리즘 입문편)에서도 그렇고 블로그에서 1번의 경우만 적용시켜서 코드를 적어놓는 경우가 많았습니다. 실제로 1번과 2번을 동시에 이용하는 것이 효율성이 높지만, 그만큼 더 이해하는데 어려움을 겪었음을 미리 밝히고 정리를 하도록 하겠습니다.

만약 코드가 잘못된 경우 댓글 남겨주시면 감사하겠습니다!!

두 가지 방식의 동작 원리를 따로 정리하고 같이 사용한 코드를 살펴보는 순서로 진행하겠습니다.

Bad Character Heuristic

Bad Character 휴리스틱의 아이디어는 간단합니다.

먼저, text의 문자와 현재 패턴의 문자가 불일치할 경우, text의 문자를 bad Character이라고 합니다.

그래서 Pattern을 이동시키는데, 두 가지 경우에 주목합니다.

  1. 패턴에 들어있는 문자를 만난 경우
  2. 패턴에 들어 있지 않은 문자를 만난 경우

이 두가지 경우가 있다는 것을 기억하고 예시를 통해서 좀 더 자세히 살펴보도록 하겠습니다.

먼저 1번의 경우를 살펴보도록 하겠습니다.

Bad Character Shift는 그나마 쉬운 편으로, 이 역시 KMP법처럼 Pattern을 얼만큼 이동할 것인지를 테이블로 만들어서 보관하고 있어야 합니다.

Case 1) 패턴에 들어가있는 문자를 만난 경우

패턴에서 일치하지 않는 문자가 마지막으로 발생한 위치를 찾습니다. 그리고 만약 패턴안에 불일치된 문자가 존재한다면, 불일치된 문자의 Index에 맞춰서 패턴을 이동시켜 줍니다.

위 예시를 보자면, 5번 위치부터 비교하는 과정에서 3번에서 불일치가 발생하였습니다. 불일치 문자는 ‘A’로 Pattern안에서 보니 1번 Index에 ‘A’ 문자가 존재합니다. 그래서 다음 비교에서 Pattern의 1번 Index가 Text의 불일치 문자 ‘A’와 비교될 수 있도록 위치를 Shift 해줍니다.

해당 경우 중요한 것은 패턴에 중복되는 문자가 나올 수 있으므로 마지막 위치의 Index를 테이블에 넣어줘야 합니다. 왜냐하면 Boyer Moore법은 뒤에서부터 비교하는 것이기 때문에 마지막 문자 Index가 아닌 다른 Index가 테이블 안에 들어가 있으면 비교 과정을 생략할 수 있기 때문입니다.

다음 예시를 살펴보자.

GCTATG
ATATFG

비교 과정에서 문자 ‘G’는 일치하지만, ‘T’와 ‘F’가 불일치 하여서 밑에 Pattern을 Shift해줘야 할 것이다.

여기서 패턴에는 문자 ‘T’가 2개 존재한다. 1번 Index와 3번 Index에 존재한다. 만약 3이 아닌 1이 테이블에 들어가 있다면 패턴의 1번 Index의 문자가 텍스트의 4번 Index 문자 ‘T’와 비교될 수 있도록 오른쪽으로 3칸 Shift될 것이다. 하지만, 이러면 3번 Index의 ‘T’와 텍스트의 ‘T’가 비교할 기회를 놓쳐버리는 것이기 때문에 문제가 발생한다. 이러한 이유때문에 마지막 Index가 들어가 있어야 하는 것이다.

그렇다면, 다음과 같은 오류도 발생 할 수 있다.

GCFTFG
AFATFG

여기서는 2번째 위치에서 불일치가 발생하였습니다.

이때 불일치 문자는 ‘F’이고 Bad Shift Table에는 ‘F’가 4로 들어가 있을 것입니다. 이때, Text의 불일치 문자의 위치와 Pattern에서 불일치 문자(’F’)의 마지막 위치를 일치시키기 위해서 Pattern을 Shift하면 어떤 현상이 발생할까요?

패턴이 뒤로 Shift 즉, 왼쪽 방향으로 Shift됩니다.

이러한 문제를 해결하기 위해서 비교 과정에서 불일치 문자가 나온 위치(포인터)의 값과 패턴에서 불일치 문자의 마지막 위치의 값을 비교하는 과정이 추가됩니다.

Case 2) 패턴에 들어가 있지 않는 문자를 만난 경우

만약 불일치 문자가 패턴안에 들어가 있지 않다면, 패턴의 어느 Index의 문자와 비교해도 불일치가 나올 것이기 때문에 불일치 문자의 다음 Index와 패턴의 첫번째 Index문자가 비교될 수 있도록 건너 뛰어 줍니다.

위 예시에서, 7번 위치에서 불일치 문자 ‘C’가 나왔다. 패턴을 살펴보니 ‘C’라는 문자가 존재하지 않는다. 즉, 패턴을 옮길 때 7번 위치에 걸쳐진다면 무조건 비교 과정에서 불일치가 나올 것이다.(패턴 안에 존재하지 않는 문자가 이미 들어가 있는 상태이기 때문에)

따라서, 패턴을 불일치 문자가 나온 다음 Index까지 Shift해주는 것입니다.

Good Suffix Shift

Bad Character Heuristic과 마찬가지로, Pattern을 전처리하여 배열을 만드는 것이 필요합니다.

먼저 그림을 통해 살펴보자.

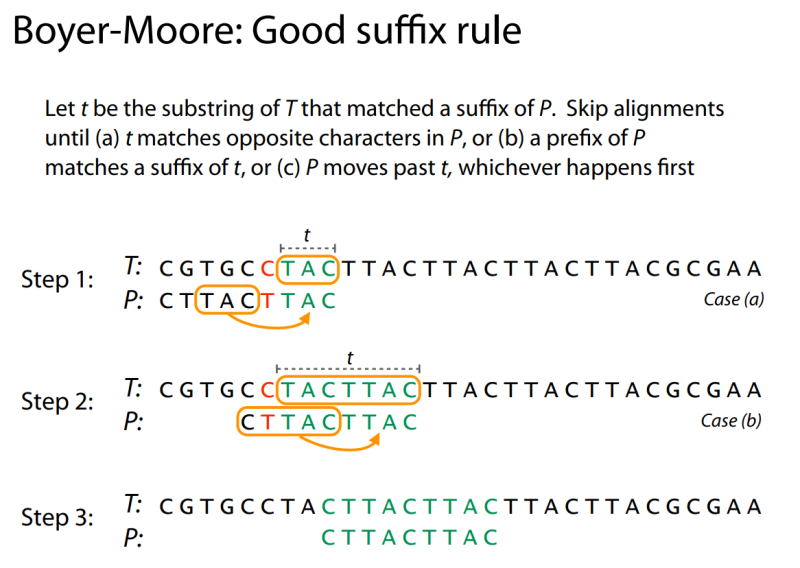
그림 1처럼 불일치 지점이 발생했을 때, 일치한 지점의 접미부와 대응 되는 접두부를 찾아서 패턴의 위치를 이동시켜 본문의 검색을 skip하는 것이다. Step 1에서는 ‘TAC’까지 일치했고 접두부에 ‘TAC’가 일치한 부분이 있다. 이를 이동시키고 다시 패턴의 오른쪽부터 비교를 한다. Step2에서는 일치한 부분이 접두부에서는 ‘CTTAC’까지 일치해서 이 부분을 맞춰 이동시키고 다시 패턴의 오른쪽부터 검사한 상황입니다.

이러한 방식으로 일치하는 부분의 접미부와 패턴의 접두부를 활용하여 이동시키는 것이 Good Suffix Shift입니다. 이 방식에도 3가지 Case가 존재합니다. 텍스트를 T, 패턴을 P, 일치하는 부분 문자열을 t라고 할때 다음과 같습니다.

  1. 패턴 P에서의 다른 부분에 문자열 t가 존재하는 경우
  2. 패턴 P의 prefix가 텍스트 T안의 t의 suffix와 일치 할 때 까지 패턴을 이동
  3. 패턴 P가 t를 지날 때까지 패턴을 이동

순서대로 살펴봅시다.

Case 1) 패턴 P에서의 다른 부분에 문자열 t가 존재하는 경우

패턴 P에서 t가 여러번 존재할 수 있다. 이러한 경우에는, 텍스트 T의 t와 패턴이 정렬되게끔 패턴을 이동한다.

위 예시를 보자면, Index 2에서 불일치가 일어나기 전까지 t는 “AB”가 됩니다.(녹색)

그리고 t인 “AB”를 패턴 P에서 찾습니다. 1번 위치(노란색)에서 t와 동일한 부분을 찾았습니다. 그래서 패턴P를 2칸 이동시켜 패턴 P와 패턴 T의 t가 일치하도록 정렬해줍니다.

Case 2) 패턴 P의 prefix가 텍스트 T안의 t의 suffix와 일치 할 때 까지 패턴을 이동

이것은 패턴 P안에 문자열 t와 전부 일치하는 것이 존재하지는 않지만, 문자열 t의 접미사와는 일치하는 부분(부분문자열)이 있는 경우를 나타냅니다. 다음의 예시를 확인해 봅시다.

위 예시의 경우, 불일치가 일어나기 전까지인 t는 “BAB”(녹색)이며 2 ~ 4번 인덱스에 위치하고 있습니다. 하지만, 패턴 P에 t와 동일한 것이 없기 때문에, t의 suffix와 일치하는 것을 패턴 P의 prefix에서 찾습니다. 노란색 배경으로 칠해져 있는 “AB” Prefix를 0 ~ 1번 인덱스에서 찾았습니다. 이는 t랑 전체 동일하지는 않지만, 인덱스 3번부터인 “AB”, Suffix of t와 일치합니다.

그리고 나서 3칸을 이동해 prefix와 suffix가 일치하도록 패턴을 이동시켜 줍니다.

Case 3) 패턴 P가 t를 지날 때까지 패턴을 이동

위 두 조건이 만족하지 않는다면, 패턴이 t를 지나도록 이동시켜 줍니다.

위 예시에서 볼 수 있듯이, t인 “AB”가 패턴 P에 없습니다. 또한, t의 suffix와 일치하는 패턴 P의 prefix도 존재하지 않습니다. 이러한 경우 인덱스 4번까지 일치하는 것을 패턴에서 찾을 수 없기 때문에 t 다음으로 패턴 P를 이동시킵니다.(Index 5)

여기서 Case 2번의 경우 좀 더 효율적으로 구현이 가능합니다.

Strong Good Suffix Heuristics

텍스트 T의 t와 일치하는 패턴 P의 부분을 t (P([i to n])라 하고, 일치하지 않는 문자를 c (P[i - 1])이라고 했을 때, case 1과 다르게, c가 앞에 존재하지 않는 t를 패턴 P에서 검색한다. 가장 가까운 위치에서 발생한 곳으로 패턴 P를 움직여 줍니다.

예를 들어서, t = P[7 to 8] 이고, c = “C” 인 상황이다.

패턴 P에서 t를 검색해보면, 4번 인덱스에서 처음으로 등장합니다. 하지만, 4번 Index 앞의 문자가 “C”이기 때문에 c 와 동일한 문자인 상황(Pattern에서 Index 3번 문자와 6번 문자)입니다.
그래서 만약 패턴 P의 4번 Index가 텍스트의 7번 Index와 비교되게끔 Shift한다고 한들 불일치 상황이 발생할 것입니다.
따라서, 4번 Index를 건너 뛰고 다시 찾습니다. 인덱스 1번 자리에서 노랜색 배경의 t가 등장하는데, 이때 앞의 문자가 c 와 동일하지 않는 문자이기 때문에 패턴을 6번 옮겨 텍스트 T의 t와 패턴 P의 t가 일치하도록 옮겨줍니다.

해당 글에서는 이 방식까지는 구현하지 않았습니다.

동작 순서

결국 Boyer-Moore 알고리즘의 동작 순서는 다음과 같습니다.

  1. 패턴의 오른쪽 끝부터 비교를 시작합니다.
  2. 비교 중인 문자가 일치하면, 왼쪽으로 한 칸씩 이동하여 다시 비교합니다.
  3. 비교 중인 문자가 일치하지 않으면, bad character rule과 good suffix rule을 적용하여 패턴을 이동합니다.
  4. 텍스트의 끝까지 비교를 마칠 때까지 위의 과정을 반복합니다.

이때, 3번 과정에서 비교하는 과정 전에 만들어 놨던 테이블을 이용하여 두 값을 비교하여 더욱 많이 Shift할 수 있는 숫자를 선택해서 패턴을 이동시켜 주면 됩니다.

코드

코드는 두 가지 경우로 나눠서 올리겠습니다.

  1. Bad Character Heuristic만 사용한 경우
  2. 두 가지 방식 혼용한 경우

Only Bad Character Rule

int bmMatch(String txt, String pat) {
  int pt, pp;                   // txt 커서, pat 커서
  int txtLen = txt.length();    // txt의 문자 개수 
  int patLen = pat.length();    // pat의 문자 개수 
  int[] skip = new int[Character.MAX_VALUE + 1];    // 건너뛰기 표 

  // 건너뛰기 표 만들기 
  for(pt = 0; pt <= Character.MAX_VALUE; pt++)
    skip[pt] = patLen;

  for(pt = 0; pt < patLen - 1; pt++)
    skip[pat.charAt(pt)] = patLen - pt - 1;   // pt == patLen - 1

  // 검색 
  while(pt < txtLen) {
    pp = patLen - 1;     // pat의 끝 문자에 주목 
    while (txt.charAt(pt) == pat.charAt(pp)) {
      if(pp == 0)
        return pt;    // 검색 성공 
      pt--;

    // 따라서, pp = patLen - 1 로 옮겨주고 pt의 경우 (patLen - 1) - pp)만큼 움직였으므로 pt += (patLen - 1) - pp) + 1 로 해주면서 결과적으론 처음 상황에서 한 칸 Shift된 상황인 것이다.
    pt += (skip[txt.charAt(pp)] > patLen - pp) ? skip[txt.charAt(pp)] : patLen - pp;
  }
  return -1;    // 검색 실패 
}

Bad Character Heuristic + Good Suffix Heuristic

int perfectBmMatch(String txt, String pat) {
  int txtLen = txt.length();
  int patLen = pat.length();
  int[] badSkip = new int[Character.MAX_VALUE + 1];
  int[] goodSkip = new int[patLen];

  int shift = 0, pt = 0;

  // badSkip initiallize
  // 전부 -1로 초기화
  for(; pt <= Character.MAX_VALUE + 1; pt++)
    badSkip[pt] = -1;

  // value == Index
  for(pt = 0; pt < patLen - 1; pt++)
    badSkip[pat.charAt(pt)] = pt;       // pt = patLen - 1

  // goodSkip initiallize

  for(int i = 0; i < patLen; i++) {
    goodSkip[i] = patLen;
  }

  int pp = 0;
  while (pt > 0) {
      while (pp >= 0 && pat.charAt(pt + pp) == pat.charAt(pp)) {
      pp--;
    }
    if(pp < 0) {
      for(; pt + pp >= 0; pp--) {
        goodSkip[pt + pp] = pt;
      }
    }
    else {
      goodSkip[pt + pp] = pt;
    }
    pp = patLen - pt;
    pt--;
  }
  
  while (shift <= txtLen - patLen) {
    pp = patLen - 1;
    while(pp >= 0 && txt.charAt(shift + pp) == pat.charAt(pp))
      pp--;
    
    if(pp < 0 ) {
      return shift;
      // 만약 여러개 구하고 싶다면
      // List<Integer>에 add 해주고 이후에도 진행하고 싶다면
      // shift += goodskip[0]
    }

    // badShift 구하는 과정
    // 여기서 max function을 사용하는 이유는 확실히 양수를 얻기 위함에 있다.
    // Negative Shift를 얻을 수 있는데 만약, 비교 과정에서 불일치할 때의 txt의 bad Character가 pattern에서 pp index보다 오른쪽에 위치해 있다면
    // 음수가 나올 것이다. (pp, badSkip Ele = index) 참고: https://greatzzo.tistory.com/8
    int badShift = Math.max(pp - badSkip[txt.charAt(shift + pp)], 1);
    int goodShift = goodSkip[pp];

    shift += goodShift > badShift ? goodShift : badShift;
  }
  return shift;
}

특징

  1. 패턴을 뒤에서부터 비교하여 탐지한다.
  1. Bad Character Rule + Good Suffix Rule

시간 복잡도

텍스트의 문자열 길이를 m이라고 하고 패턴의 문자열 길이를 n이라고 할 때, 시간 복잡도는 다음과 같습니다.

T(n) = O(m/n)

Reference

profile
서정범
개발정리블로그
이전 포스트

[Java] KMP

다음 포스트

[Java] 이진 트리(Binary Tree) + 이진 탐색 트리(Binary Search Tree)

post-custom-banner

0개의 댓글