이진 트리

이진 트리란?

이진 트리(Binary Tree)는 자식 노드가 최대 두개인 노드들로 구성된 트리를 의미합니다.

이 두개의 자식 노드는 왼쪽 자식 노드, 오른쪽 자식 노드로 나눌 수 있습니다.

이진 트리는 모든 노드가 정확하게 두개의 서브 트리를 가지고 있는 것과 마찬가지인데, 다만 서브 트리는 공백이 될 수 있습니다. 즉, 노드의 유한 집합으로서 공백이거나 루트와 두개의 분리된 이진트리인 경우 왼쪽 서브트리와 오른쪽 서브트리로 구성됩니다.

이러한 특성에 의거하여 3가지 종류의 트리를 가지고 있습니다.

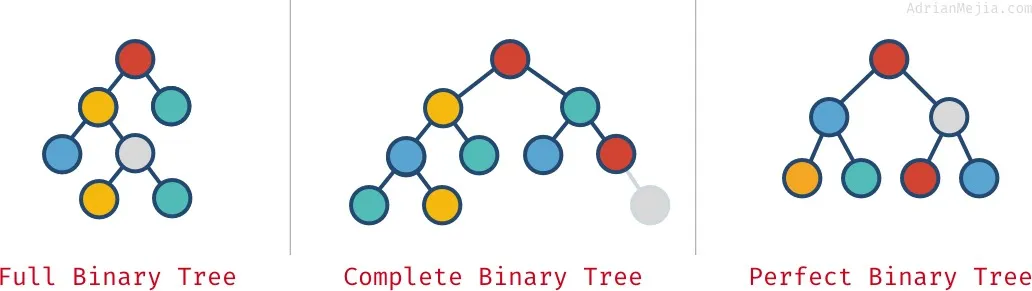
1. 정 이진 트리(Full Binary Tree): 각 노드가 0개 혹은 2개의 자식 노드를 갖는다.
2. 완전 이진 트리(Complete Binary Tree): 마지막 레벨을 제외한 모든 노드가 가득 차있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 한다.
3. 포화 이진 트리(Perfect Binary Tree): 정 이진트리이면서 완전 이진 트리인 경우이다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리

추가적으로 편향 이진 트리(Skewed Binary Tree)도 존재 합니다.

이진 탐색 트리

이진 탐색 트리란?

이진 탐색 트리(Binary Search Tree)는 이진 탐색(Binary Search) + 연결 리스트(Linked List)를 결합한 이진 트리입니다. 이진 탐색 트리도 또한 최대 두 개인 자식 노드들로 구성되는 트리입니다.

이진 탐색의 효율적인 탐색 능력을 유지하면서 빈번한 자료 입력과 삭제를 가능하게끔 고안되었습니다.

이진 탐색 트리는 다음과 같은 특징을 가지고 있습니다.

특징

1. 각 노드에 중복되지 않는 키(Key)가 있다.

2. 루트 노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.

3. 루트 노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.

4. 좌우 서브 트리도 모두 이진 탐색 트리여야 한다.

동작 과정

1. 루트 노드의 키와 찾고자 하는 값을 비교, 만약 찾고자 하는 값이라면 탐색을 종료한다.
2. 찾고자 하는 값이 루트 노드의 키보다 작다면, 왼쪽 서브 트리로 탐색을 진행
3. 찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행
4. 이 과정을 찾고자 하는 값을 찾을 때까지 반복해 진행한다.

찾고자 하는 노드의 높이가 h라면, $O(h)$만큼의 시간이 소요될 것입니다.

탐색 시간 복잡도

트리의 높이가 h라면, 트라 안에 찾고자 하는 값이 있든 없든 최대 h번의 연산 및 탐색이 진행됩니다.

코드

사실 이진 트리와 이진 탐색 트리의 경우 코드가 정말 너무 길어서 Github Page Link를 올려 놓는점 양해 부탁드립니다.

Github/JeongBeomSeo -> 이진 트리, 이진 탐색 트리

---

Reference

• [Data Structure] Java 이진트리(Binary Tree) 구현
• 자바 [JAVA] - Binary Search Tree (이진 탐색 트리) 구현하기
• 자바 [JAVA] - Binary Search Tree (이진 탐색 트리) 구현하기 - Generic