DFS & BFS

개념

DFS는 깊이 우선 탐색으로, 한 노드에서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식을 말합니다. 스택 혹은 재귀 함수를 사용해서 구현할 수 있습니다.

BFS는 너비 우선 탐색으로, 특정 노드에서 탐색을 시작하여 같은 레벨에 있는 모든 노드를 탐색한 후 다음 하위 레벨로 내려가 탐색을 진행하는 방식입니다. 큐를 이용하여 구현할 수 있습니다.

구현 방식

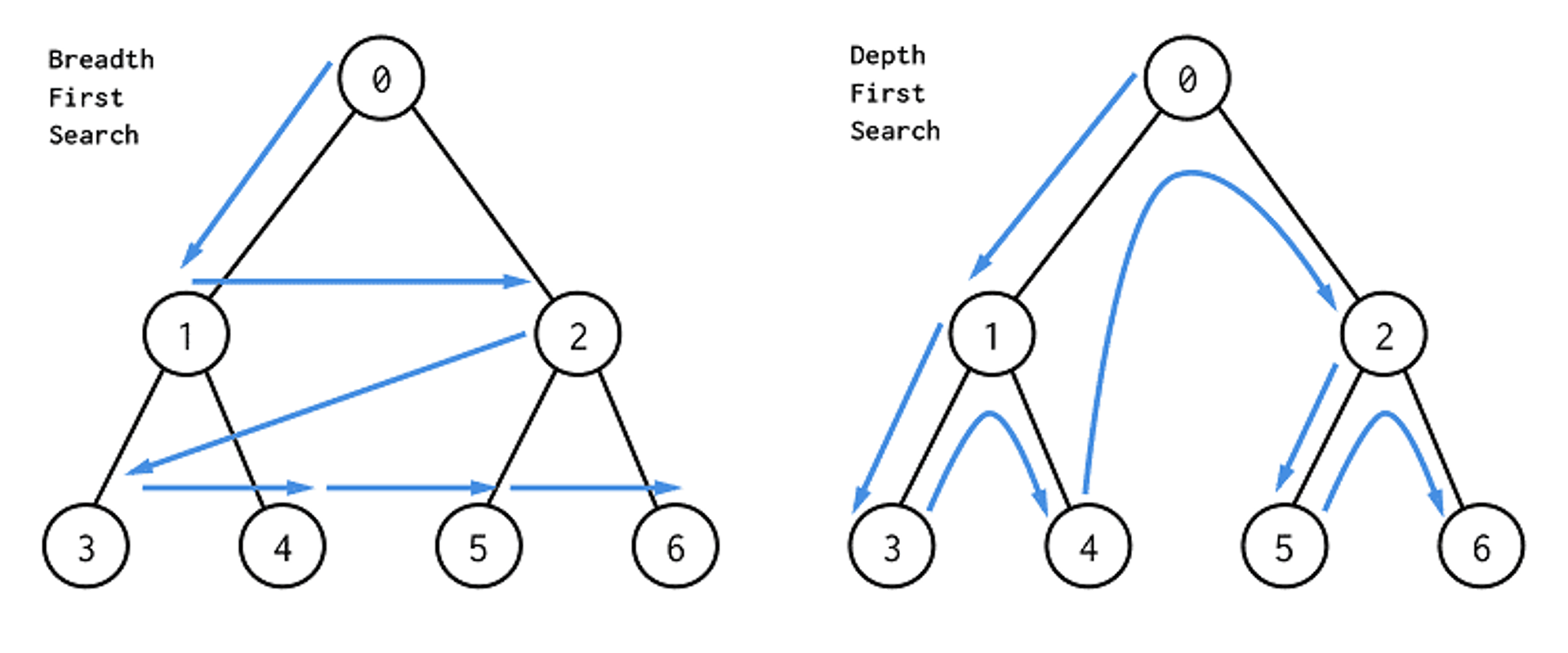
DFS

1. 시작 정점을 방문
2. 자식을 모두 탐색
3. 이때 연결된 자식 노드가 존재하지 않을 때까지 들어갔다면 다시 되돌아 온다.
4. 되돌아 오는 과정에서 다른 자식 노드가 있다면 방문 후 되돌아 오는 과정을 반복하면서 모든 노드 방문

BFS

1. 시작 정점을 방문
2. 시작 정점에 인접한 모든 정점들을 우선 방문
3. 더 이상 방문 할 정점이 없으면 다음 레벨로 내려간다.
4. 다시 인접한 모든 정점들을 우선 방문

장단점

DFS

장점

1. 최선의 경우, 가장 빠른 알고리즘이다. “운 좋게” 해에 도달하는 올바른 경로를 선택한다면, 최소 실행시간에 해를 찾는다.

2. BFS에 비해 저장공간의 필요성이 적다. 백트래킹을 해야하는 노드들만 저장해주면 된다.

단점

1. 찾은 해가 최적이 아닐 가능성이 있다.

2. 최악의 경우, 가능한 모든 경로를 탐험하고나서야 해를 찾으므로, 해에 도달하는 데 가장 오래 시간 소모

BFS

장점

1. 너비를 우선으로 탐색하기 때문에 답이 되는 경로가 여러 개인 경우에도 최단 경로를 보장

단점

1. 최소 실행시간보다는 오래 걸릴다는 것이 거의 확실

2. 최악의 경우, 실행에 가장 긴 시간이 걸릴 수 있다.

코드

DFS

// Using Recursive Function
void DFS(int node) {

  visited[node] = true;
  System.out.print(node + " -> ");

  for(int childNode : graph[node]) {
    if(!visited[childNode]) {
      DFS(childNode);
    }
  }
}

// Using Stack
void DFS(int start) {
  Stack<Integer> stack = new Stack<>();

  stack.add(start);
  System.out.print(start + " -> ");
  visited[start] = true;

  while(!stack.isEmpty()) {
    int curNode = stack.peek();

    boolean hasNearNode = false;
    for(int nearNode : graph[curNode]) {
      if(!visited[nearNode]) {
        visited[nearNode] = true;
        System.out.print(nearNode + " -> ");
        hasNearNode = true;
        stack.add(nearNode);
        break;
      }
    }
    if(!hasNearNode) stack.pop();
  }
}

BFS

// Using Queue
void BFS(int start) {
  Queue<Integer> q = new LinkedList<>();

  q.add(start);
  visitied[start] = true;

  while (!q.isEmpty()) {
    int curNode = q.poll();

    System.out.print(curNode + " -> ");

    for(int adjNode : graph[curNode]) {
      if(!visitied[adjNode]) {
        q.add(adjNode);
        visitied[adjNode] = true;
      }
    }
  }
}

시간 복잡도

DFS와 BFS는 인접행렬로 구현하는냐, 인접리스트로 구현하는냐에 따라 시간 복잡도가 다르게 나옵니다.

DFS

• 인접 행렬
  DFS 하나당 N번의 loop를 돌게 되므로 $O(n)$의 시간복잡도를 가진다. 그런데 N개의 정점을 모두 방문해야 하므로 $n*O(n)$이므로 $O(n^2)$의 시간복잡도를 가지게 된다.
  

• 인접 리스트
  DFS가 총 N번 호출되긴 하지만 인접행렬과 달리 인접 리스트로 구현하게 되면 DFS하나당 각 정점에 연결되어 있는 간선의 개수만큼 탐색을 하게 되므로 예측이 불가능하다. 하지만 DFS가 다 끝난 후를 생각하면, 모든 정점을 한번씩 다 방문하고, 모든 간선을 한번씩 모두 검사했다고 할 수 있으므로 $O(n+e)$의 시간 복잡도를 가진다.
  

BFS

• 인접 행렬
  정점 한개당 N번의 for loop를 돌기 때문에 $O(n)$의 시간이 걸리는데 for loop는 큐에 아무것도 없을 때까지 즉, 모든 정점을 방문할 때까지 실행되므로 n번 반복 실행된다. 따라서 시간복잡도는 $O(n^2)$이다.
  

• 인접 리스트
  모든 간선에 대해서 한번씩 검사를 할 것이고, 각 정점을 한번씩 모두 방문하기 때문에 $(n+e)$만큼의 시간복잡도를 가질 것이다.