[JAVA] 다이나믹 프로그래밍

서정범·2023년 4월 3일
DPalgorithm
0

자료구조와 알고리즘

목록 보기
6/30

다이나믹 프로그래밍(DP)이란?

다이나믹 프로그래밍은 메모리를 적절히 사용하여 수행 식이나 효율성을 비약적으로 향상시키는 방법입니다.

이미 계산된 결과(작은 문제)는 별도의 메모리 영역에 저장하여 다시 계산하지 않도록 합니다.

다이나믹 프로그래밍은 동적 계획법이라고도 부릅니다.

동적(Dynamic)

  • 자료 구조에서 동적 할당(Dynamic Allocation)은 '프로그램이 실행되는 도중에 실행에 필요한 메모리를 할당하는 기법'입니다.
  • 반면에 다이나믹 프로그램에서 '다이나믹'은 별다른 의미 없이 사용된 단어입니다.

사용 조건

예를 들어, 완전 탐색 같은 경우 해결한 문제를 반복적으로 수행하면서 굉장히 비효율적인 측면을 보여주는데 이러한 것을 해결하는데 효율적입니다.

따라서, 다이나믹 프로그래밍은 이러한 문제를 해결하는데 사용하고 다음의 조건을 만족할 때 사용할 수 있습니다.

  1. 최적 부분 구조(Optimal Substructure)
    • 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있습니다.
  2. 중복되는 부분 문제(Overlapping Subproblem)
    • 동일한 작은 문제를 반복적으로 해결해야 합니다.

대표적으로 사용되는 문제

피보나치 수열

다음의 점화식을 확인해보자.

Fn=Fn−1+Fn−2F_n = F_{n-1} + F_{n-2}

이러한 식을 피보나치 수열이라고 합니다.

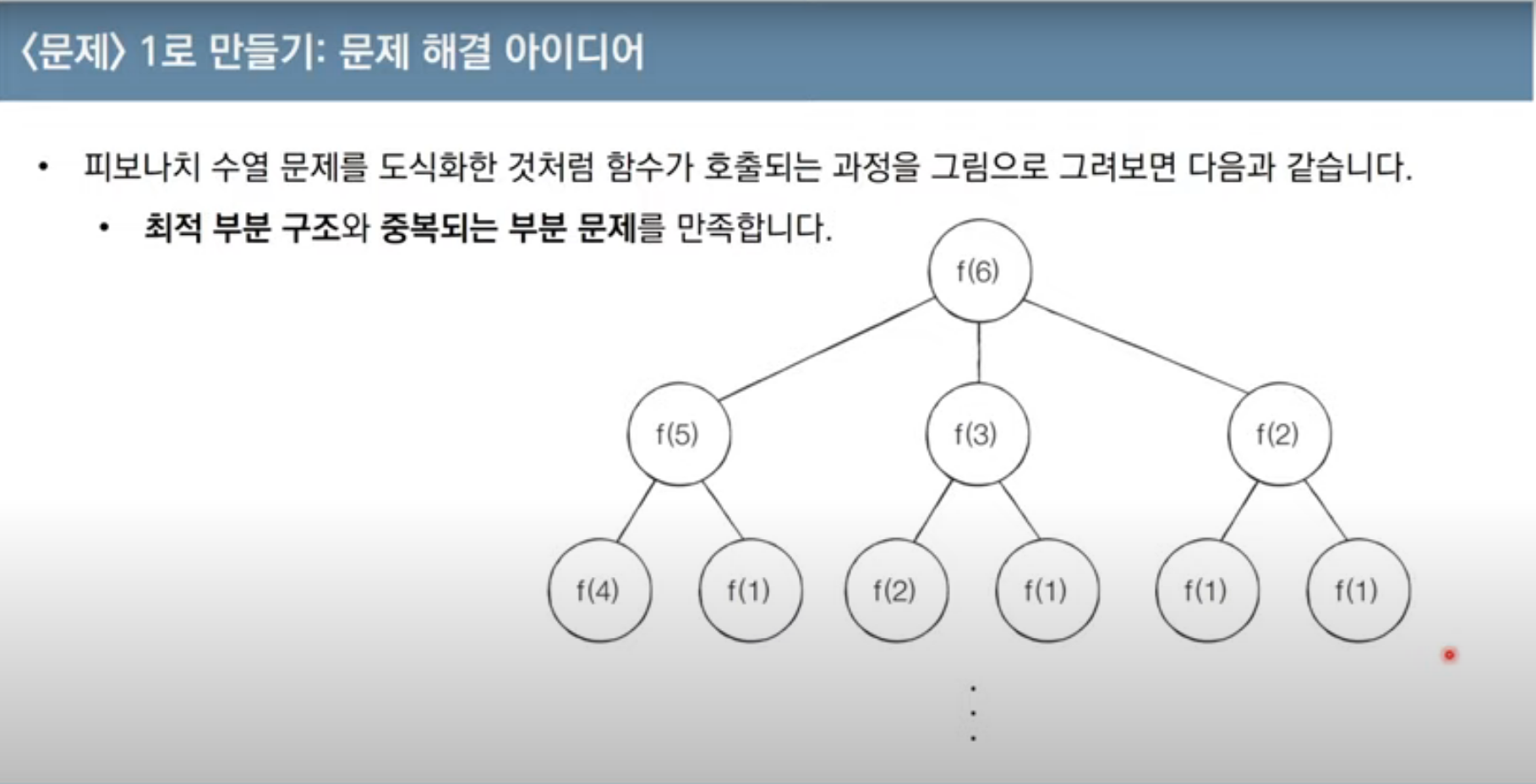
  • 피보나치 수열이 계산되는 과정은 다음과 같이 표현할 수 있습니다.
    • 프로그래밍에서는 이러한 수열을 배열이나 리스트를 이용해 표현합니다.

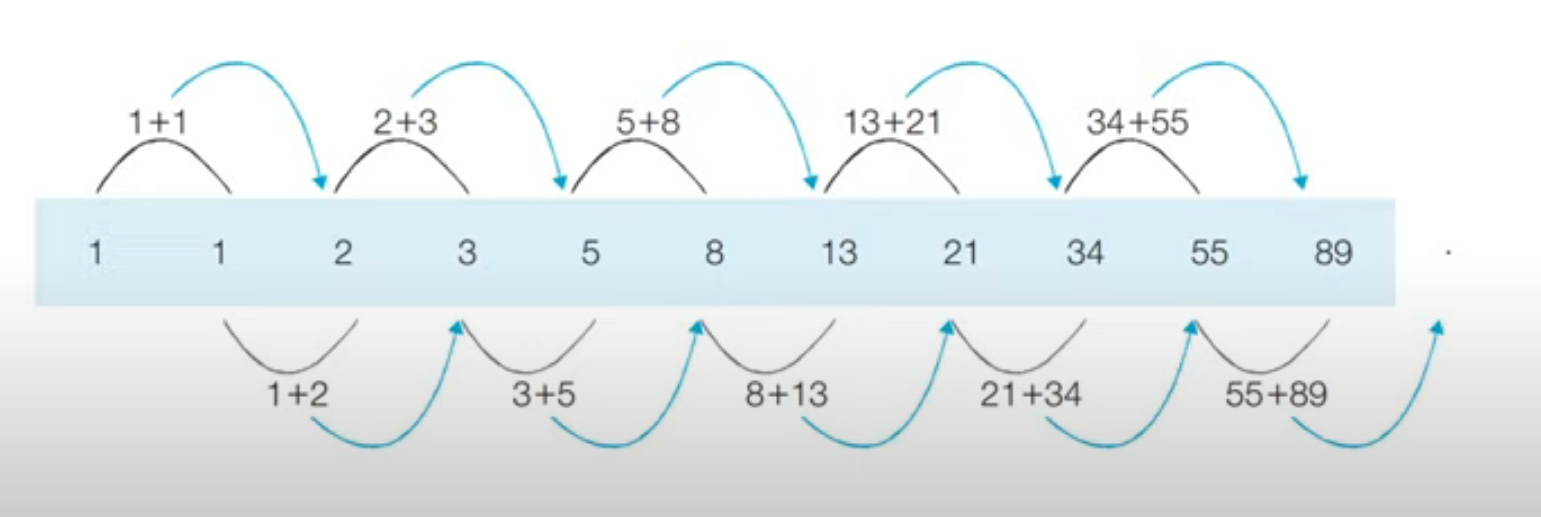
도식화한 모습은 다음과 같습니다.

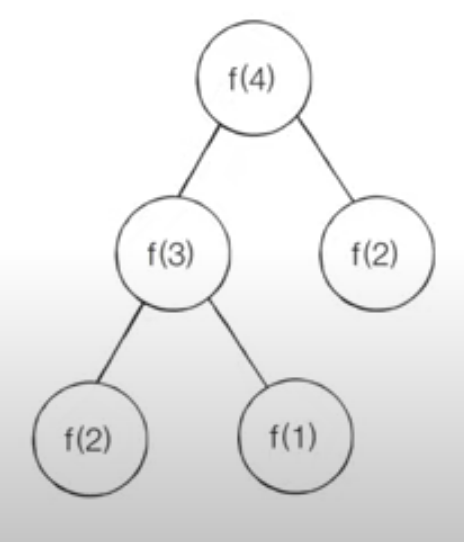
단순 재귀함수로 피보나치 수열을 해결하면 지수 시간 복잡도를 가지게 됩니다.

  • Layer 1 -> 1
  • Layer 2 -> 2
  • Layer 3 -> 4
  • layer n -> 2n−12^{n-1}

피보나치 수열을 일반적인 방식으로 푼다면 시간 복잡도는 O(2n)O(2^n)입니다.

동작 방식

다이나믹 프로그래밍의 구현은 일반적으로 두 가지 방식으로 구현됩니다.

  • Top-Down 방식
  • Bottom-Up 방식

두 방식을 알아보기 전에 Top-Down에서 사용되는 메모이제이션(Memoization)을 살펴보고 가자.

메모이제이션(Memoization)

메모이제이션은 다이나믹 프로그래밍을 구현하는 방법 중 하나입니다.

한 번 계산된 결과를 메모리 공간에 메모하는 기법입니다.

  • 같은 문제를 다시 호출하면 메모했던 겨과를 그대로 가져옵니다.
  • 값을 기록해 놓는다는 점에서 캐싱(Caching)이라고도 합니다.

Top-Down vs Bottom-Up

탑다운(Memoization) 방식은 하향식이라고도 하며 바텀업 방식은 상향식이라고도 합니다.

다이나믹 프로그래밍의 전형적인 형태는 바텀업 방식입니다.

  • 반복문 활용
  • 결과 저장용 리스트는 DP 테이블이라고 부릅니다.

엄밀히 말하면 메모이제이션은 이전에 계산된 견과를 일시적으로 기록해 놓는 넓은 개념을 의미합니다.

  • 따라서 메모이제이션은 다이나믹 프로그래밍에 국한된 개념은 아닙니다.
  • 한 번 계산된 견과를 담아 놓기만 하고 다이나믹 프로그래밍을 위해 활용하지 않을 수도 있습니다.

두가지 방식으로 구현한 소스 코드를 확인해 봅시다.

먼저, 탑다운 방식입니다.

```java
  // 한번 계산된 결과를 메모이제이션(Memoization)하기 위한 리스트 초기화
  int[] dp = new int[101];

  // 피보나치 함수(Fibonacci Function)을 재귀함수로 구현(탑다운 다이나믹 프로그래밍)
  int fibo(int x) {
  // 종료 조건 (1 혹은 2일 때 1을 반환)
  if (x == 1 || x == 2) return 1;

  // 이미 계산한 적이 있는 문제라면 그대로 반환
  if (dp[x] != 0) return dp[x];

  // 아직 계산하지 않은 문제라면 점화식에 따라서 피보나치 결과 반환
  dp[x] = fibo(x - 1) + fibo(x - 2);
  return dp[x];
}

다음은 바텀업 방식입니다.

public static void main(String[] args) {
  // 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
  int[] dp = new int[101];

  //첫 번째 피보나치 수와 두 번째 피보나치 수는 1
  dp[1] = 1;
  dp[2] = 1;
  int n = 100;

  // 피보나치 함수(Fibonacci Function) 반복문으로 구현(바텀업 다이나믹 프로그래밍)
  for (int i = 3; i < n + 1; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }

  System.out.println(dp[i]);
}

피보나치 후열: 메모이제이션 동작 분석

이미 계산된 결과를 메모리에 저장하면 다음과 같이 색칠된 노드만 처리할 것을 기대할 수 있습니다.

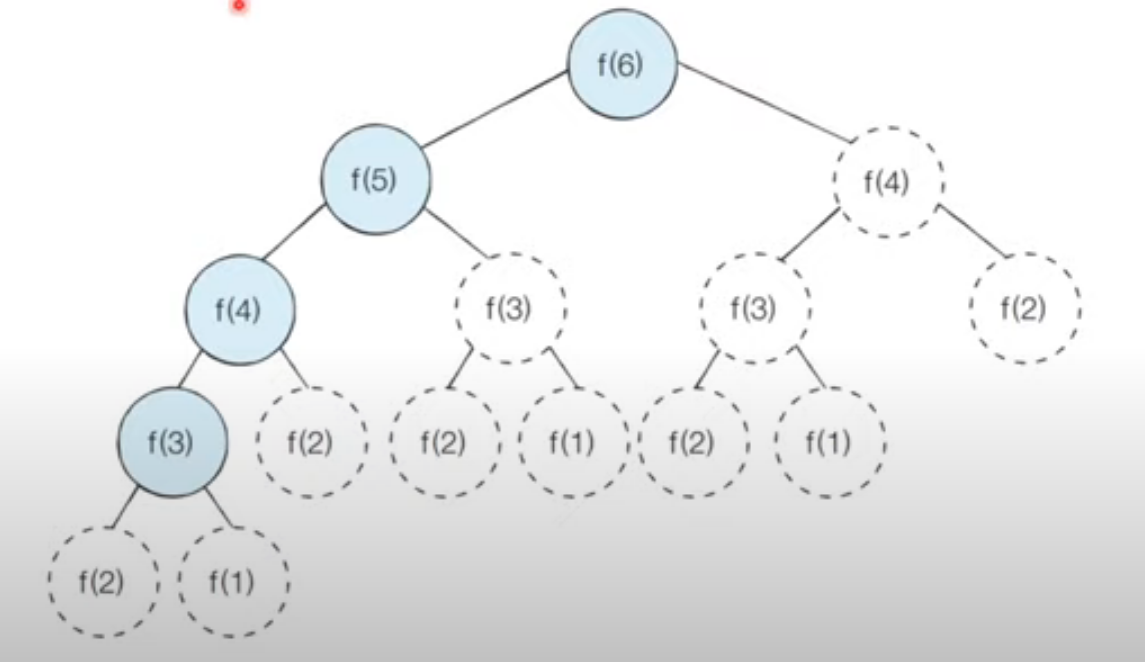
좀 더 나아가서 방문한 노드만 표시를 해보자면 다음과 같습니다.

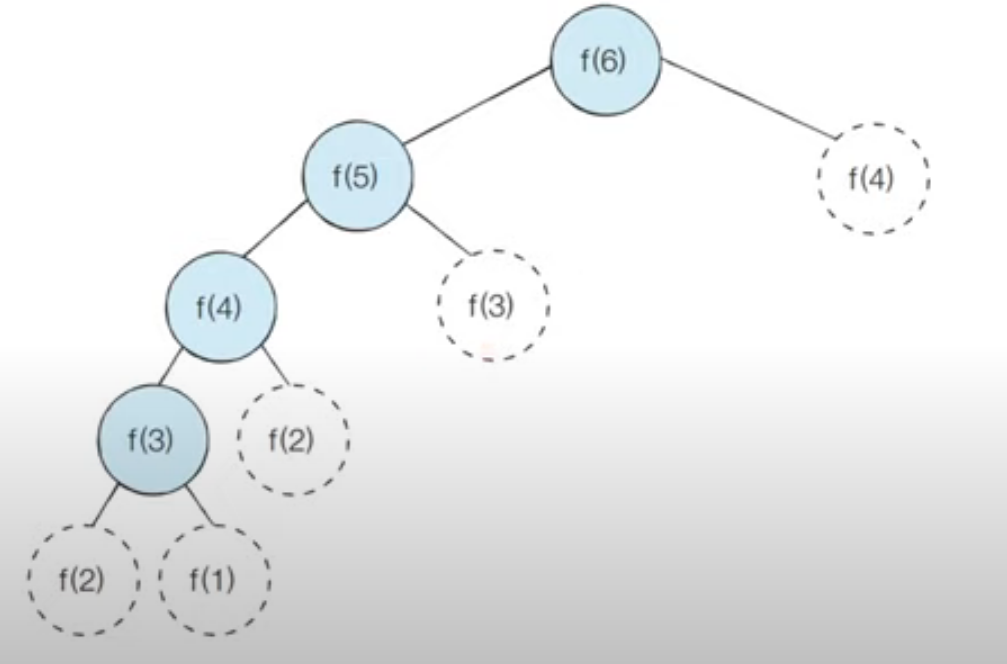
따라서, 메모이제이션을 이용하는 경우 피보나치 수열 함수의 시간 복잡도는 O(N)O(N)입니다.

다이나믹 프로그래밍 vs 분할 정복

  • 다이나믹 프로그래밍과 분할 정복은 모두 최적 부분 구조를 가질 때 사용할 수 있습니다.
    • 큰 문제를 작은 문제로 나눌 수 있으며 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는 상황
  • 다이나믹 프로그래밍과 분할 정복의 차이점은 부분 문제의 중복입니다.
    • 다이나믹 프로그래밍 문제에서는 각 부분 문제들이 서로 영향을 미치며 부분 문제가 중복됩니다.
    • 분할 정복 문제에서는 동일한 부분 문제가 반복적으로 계산되지 않습니다.

예시를 통해서 살펴보겠습니다.

분할 정복의 대표적인 예시인 퀵 정렬을 살벼봅시다.

  • 한번 기준 원소(pivot)가 자리를 변경해서 자리를 잡으면 그 기준 원소의 위치는 바뀌지 않습니다.
  • 분할 이후 해당 피벗을 다시 처리하는 부분 문제는 호출하지 않습니다.

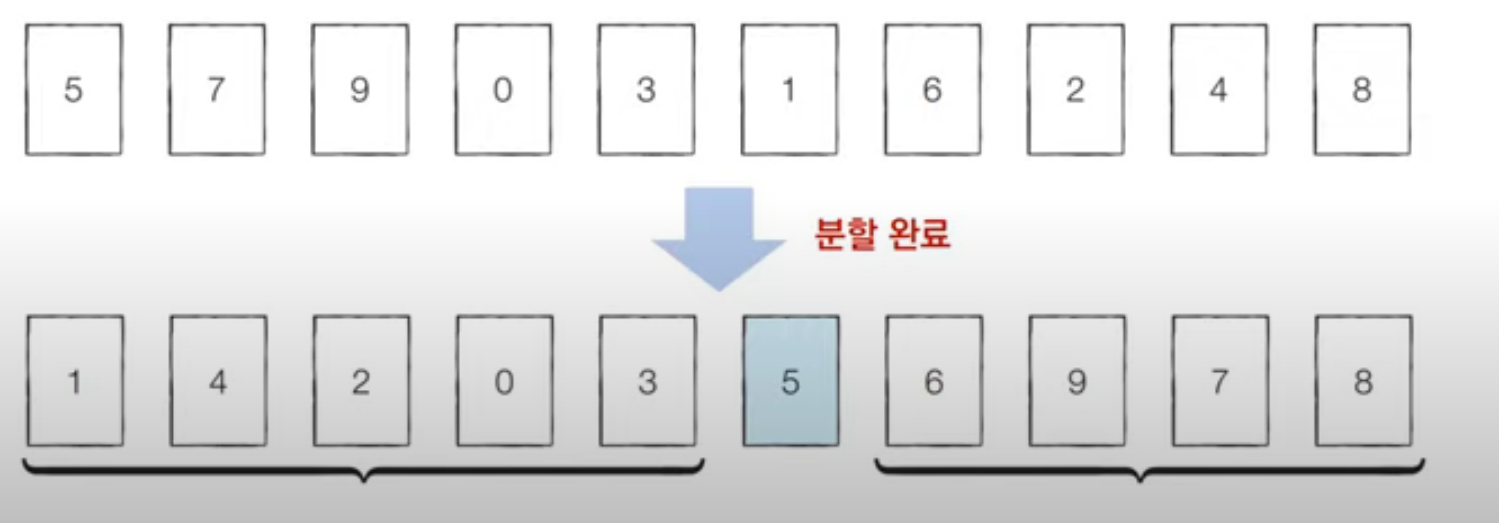
예를 들어, 5를 pivot으로 잡고 퀵 정렬을 했을 경우 아래와 같이 정렬이 됩니다.

이후 부분 문제로 나누어서 양쪽을 정렬할 때 5는 위치의 변동이 없습니다.

다이나믹 프로그래밍 문제에 접근하는 방법

  • 주어진 문제가 다이나믹 프로그래밍 유형임을 파악하는 것이 중요합니다.
  • 가장 먼저 그리디, 구현, 완전 탐색 등의 아이디어로 문제를 해결할 수 있는지 컴토할 수 있습니다.
    • 다른 알고리즘으로 풀이 방법이 떠오르지 않으면 다이나믹 프로그래밍을 고려해 봅시다.
  • 일단 재귀 함수로 비효율적인 완전 탐색 프로그램을 작성한 뒤에 (탑다운) 작은 문제에서 구한 답이 큰 문제에서 그대로 사용될 수 있으면, 코드를 개선하는 방법을 사용할 수 있습니다.
  • 일반적인 코딩 테스트 수준에서는 기본 유형의 다이나믹 프로그래밍 문제가 출제되는 경우가 많습니다.

핵심은 점화식이다.

문제를 통해서 적용해 보겠습니다.

해당 문제는 '이코테'에서 나온 문제입니다.

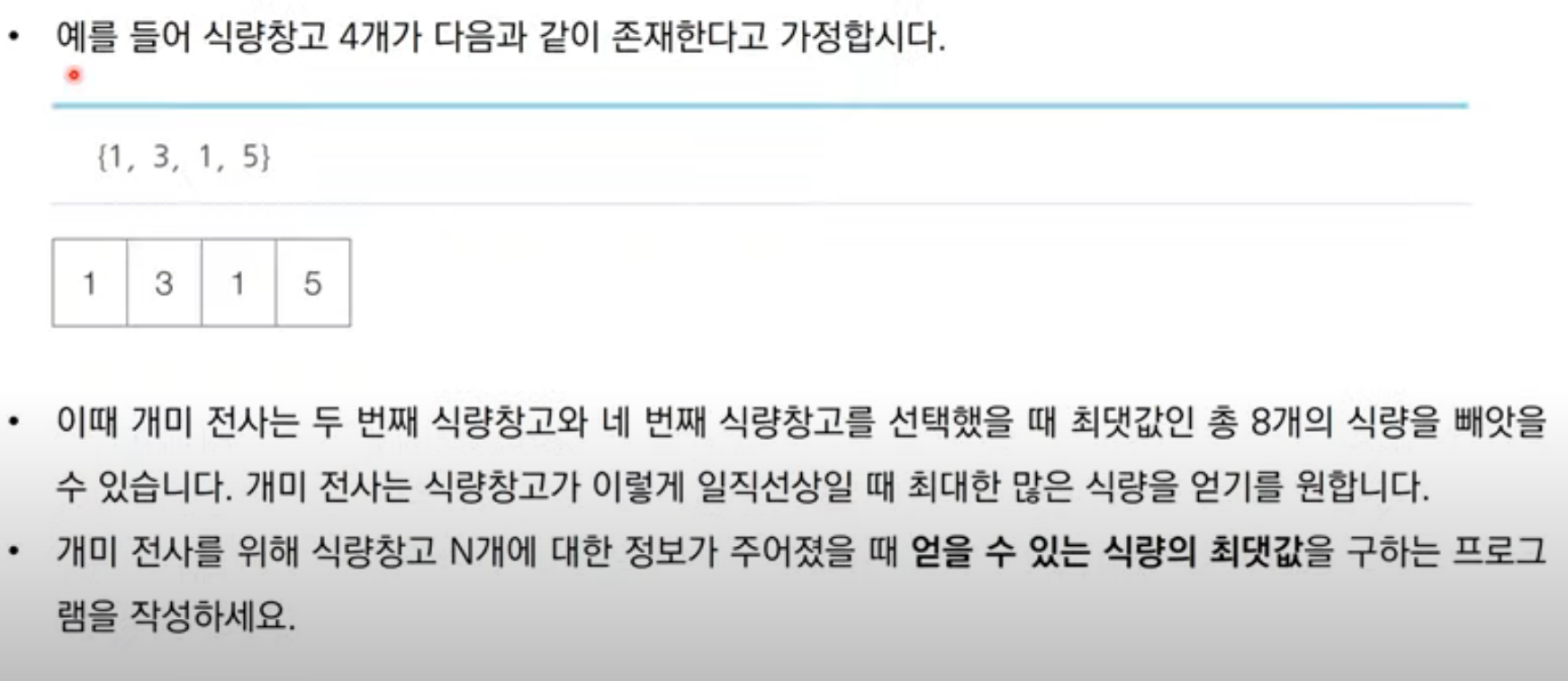
이것을 다이나믹 프로그래밍 기법으로 풀기 위해서 먼저 조건을 살펴봐야 합니다.

  1. 최적 부분 구조
  2. 중복되는 부분 문제

경우의 수를 확인해 봅시다.

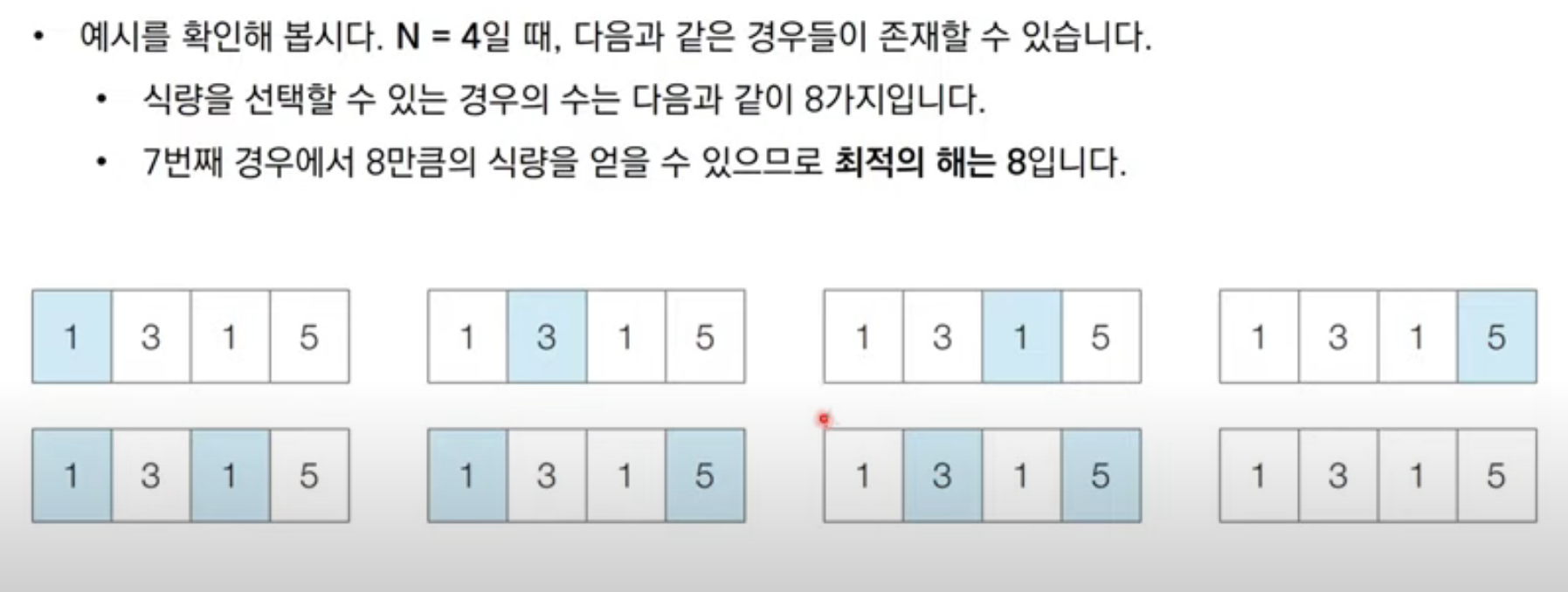
이와 같이 풀 수 있는데,

  1. 만약 0번째 창고만 확인하는 경우 0번째 창고를 선택할 수 있습니다.
  2. 0 ~ 1번째까지 확인하는 경우 0 또는 1번째 창고를 선택할 수 있습니다.
  3. 0 ~ 2번째까지 확인하는 경우 0, 2 또는 1번째 창고를 선택할 수 있습니다.
  4. 0 ~ 3번쨰까지 확인하는 경우 0, 2 또는 1, 3번째 창고를 선택할 수 있습니다.

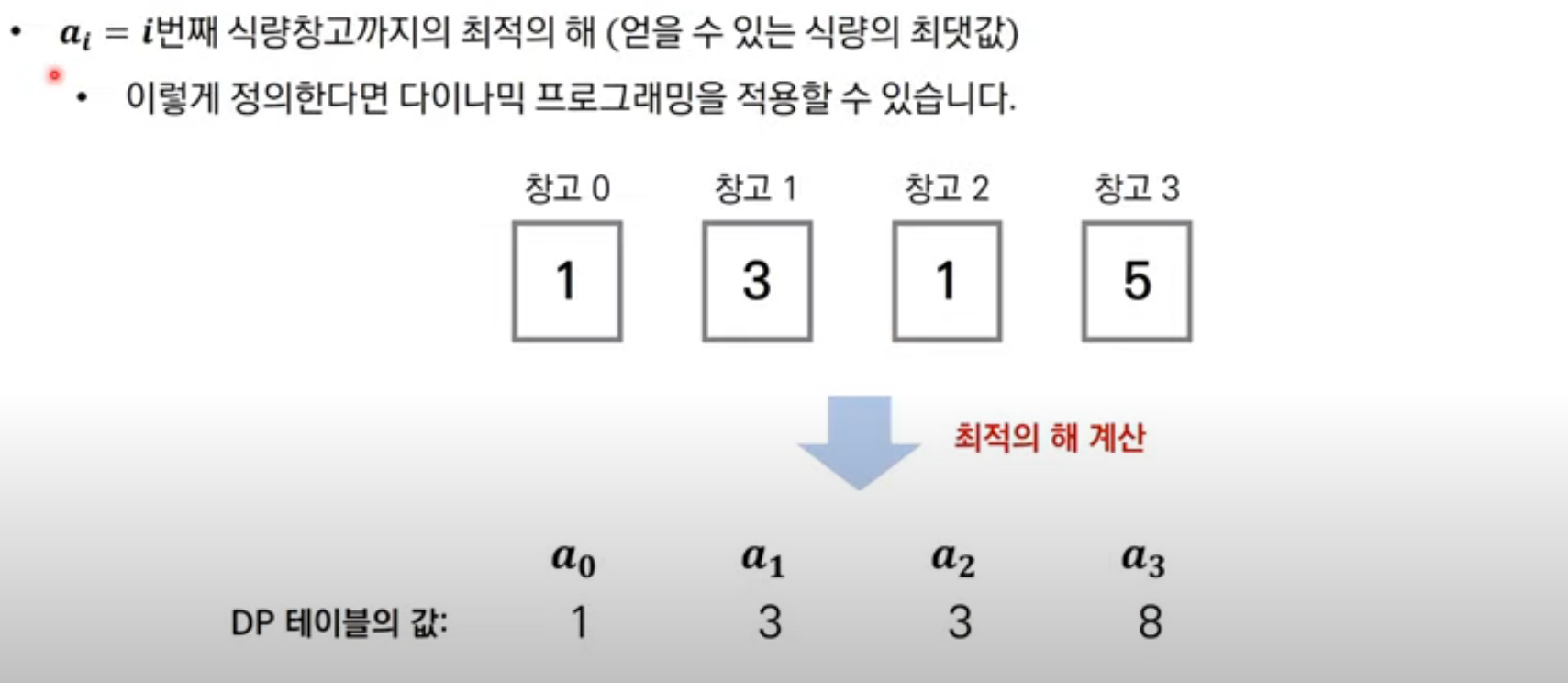
이것을 일반화 시켜보자면 다음과 같습니다.

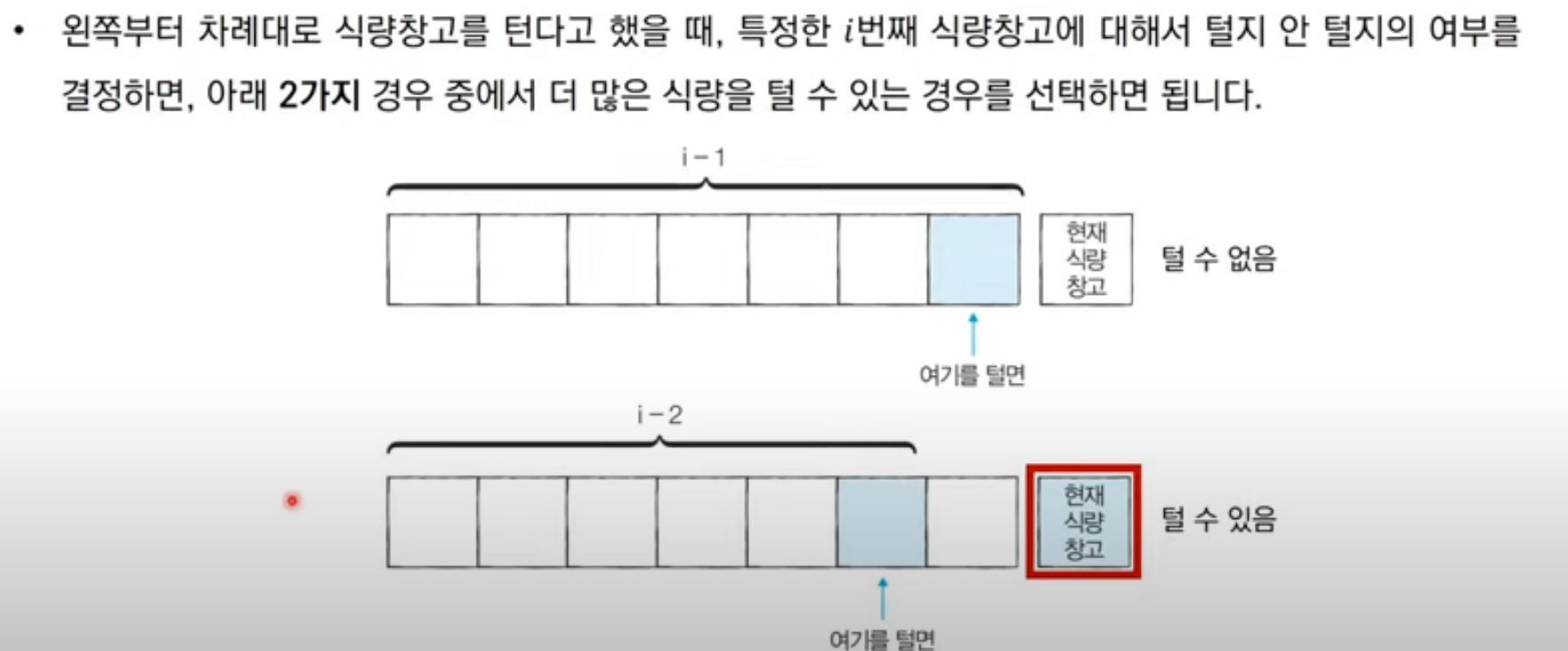
최적 부분 구조의 경우, i - 1번째와 i - 2번째를 이용해서 확인할 수 있습니다.

이를 수식적으로 표현하면 다음과 같습니다.

코드는 다음과 같습니다.

import java.util.Scanner;

public class Main {
  static int[] d = new int[100];
  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    // 정수 N을 입력받기
    int n = sc.nextInt();

    // 모든 식량 정보 입력 받기
    int[] arr = new int[n];
    for (int i = 0; i < n; i++) {
      arr[i] = sc.nextInt();
    }
    // 다이나믹 프로그래밍 (Dynamic Programming) 진행 (바텀업)
    d[0] = arr[0];
    d[1] = Math.max(arr[0], arr[1]);
    for (int i = 2; i < n; i++) {
      d[i] = Math.max(d[i - 1], d[i - 2] + arr[i]);
    }

    // 계산된 결과 출력
    System.out.println(d[n - 1]);
  }
}

다음 문제를 확인해 봅시다.

이것의 최적 부분 구조는 도식화를 통해서 확인할 수 있습니다.

해당 문제는 단순히 1보다 큰 숫자로 나누어 떨어지는 경우에 바로 나누는 것이 아닙니다.

위의 숫자 26의 경우에도 2로 나누는 것보다도 1을 빼고 나서 처리하는 것이 최소 연산으로 나옵니다.

이것을 점화식으로 표현하면 다음과 같습니다.

다음은 해당 문제의 코드입니다.

import java.util.Scanner;

public class Main {
  // 앞서 계산된 결과를 저장하기 위한 DP 테이블 초기화
  static int[] d = new int[300001];
  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    int x = sc.nextInt();
    // 다이나믹 프로그래밍 (Dynamic Programming) 진행(바텀업)
    for (int i = 2; i <= x; i++) {
      // 현재의 수에서 1을 빼는 경우
      d[i] = d[i - 1] + 1;
      // 현재의 수가 2로 나누어 떨어지는 경우
      if (i % 2 == 0)
        d[i] = Math.min(d[i], d[i / 2] + 1);
      // 현재의 수가 3으로 나누어 떨어지는 경우
      if (i % 3 == 0)
        d[i] = Math.min(d[i], d[i / 3] + 1);
      // 현재의 수가 5로 나누어 떨어지는 경우
      if (i % 5 == 0)
        d[i] = Math.min(d[i], d[i / 5] + 1);
    }
    System.out.println(d[x]);
  }
}

그 외에 '이코테'에서 주목할 만한 문제는 다음과 같습니다.

  • 효율적인 화폐 구성
  • 금광
  • 병사 배치하기(Longest Increasing Subsequences, LIS)

'이코테'의 문제가 아니라 대표적인 문제로 '타일링 문제'도 있습니다.

대표적인 문제 LIS Alogirhtm은 다음 페이지에서 정리해놨습니다.

profile
서정범
개발정리블로그
이전 포스트

트리

다음 포스트

[Java] DFS & BFS

0개의 댓글