[Java] 병합 정렬(Merge Sort)

서정범·2023년 3월 13일

Sort algorithm

자료구조와 알고리즘

목록 보기

16/30

병합 정렬

병합 정렬이란?

분할 정렬은 배열을 반으로 나눈 다음, 각 부분에서 재귀적으로 정렬을 수행하는 정렬 알고리즘입니다. 배열이 충분히 작아질 때까지 이 작업을 반복한 다음, 병합 정렬과 같이 두 부분을 합치면서 정렬을 완성합니다.

일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬에 속하며, 분할 정복 알고리즘의 하나 이다.

동작 과정

배열을 반으로 나눕니다.
각 부분에서 재귀적으로 정렬을 수행합니다.
두 부분을 병합합니다.
병합한 배열을 반환합니다.

정렬을 수행하려는 배열이 n개의 요소를 가지고 있다면, 배열을 반으로 나누는 단계에서 $log_2n$ 번의 분할 작업이 필요합니다. 각 단계에서 병합 작업을 수행하는 데에는 최대 n개의 요소를 비교하므로, 각 단계마다 O(n)의 시간 복잡도가 필요합니다.

특징

안정 정렬 + 분할 정복 알고리즘

리스트를 균등한 크기로 분할, 정렬 후 병합

장단점

장점

안정적인 정렬 방법
→ 데이터의 분포에 영향을 덜받는다. 즉, 입력 데이터가 무엇이든 간에 정렬되는 시간은 동일하다.
⇒ $O(log_2n)$ 로 동일

만약 레코드를 연결 리스트(Linked List)로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아진다.
-> 제자리 정렬(in-place sorting)로 구현할 수 있다.
=> 따라서 크기가 큰 레코드를 정렬할 경우에 연결 리스트를 사용한다면, 병합 정렬은 퀵 정렬을 포함한 다른 어떤 정렬 방법보다도 효율적이다.

단점

만약 레코드를 배열(Array)로 구상하면, 임시 배열이 필요하다.
-> 제자리 정렬(in-place sorting)이 아니다.

레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초래한다.

코드

// 병합 정렬
static int[] buff;    // 작업용 배열

// a[left] ~ a[right]를 재귀적으로 병합 정렬
static void __mergeSort(int[] a, int left, int right) {
  if(left < right) {
    int i;
    int center = (left + right) / 2;
    int p = 0;
    int j = 0;
    int k = left;

    __mergeSort(a, left, center);          // 배열의 앞부분을 병합 정렬합니다.
    __mergeSort(a, center + 1, right);     // 배열의 뒷부분을 병합 정렬합니다.

    // 앞부분을 작업용 배열에 넣어주기
    for(i = left; i <= center; i++)
      buff[p++] = a[i];

    // 앞부분과 뒷부분 배열 비교하면서 배열 a에 저장
    while (i <= right && j < p)
      a[k++] = (buff[j] <= a[i]) ? buff[j++] : a[i++];

    // 앞부분에 남아 있는 요소 배열 a에 복사
    while (j < p)
      a[k++] = buff[j++];
  }
}

// 병합 정렬
static void mergeSort(int[] a, int n) {

  buff = new int[n];           // 작업용 배열을 생성합니다.

  __mergeSort(a, 0, n - 1);    // 배열 전체를 병합 정렬 합니다.

  buff = null;                 // 작업용 배열을 해체합니다.
  
}

시간 복잡도

먼저, 병합 정렬의 경우 분할 단계 → 병합 단계로 나누어서 생각할 수 있다.

분할 단계

분할 단계에서는 비교 연산과 이동 연산이 수행되지 않는다.

병합 단계

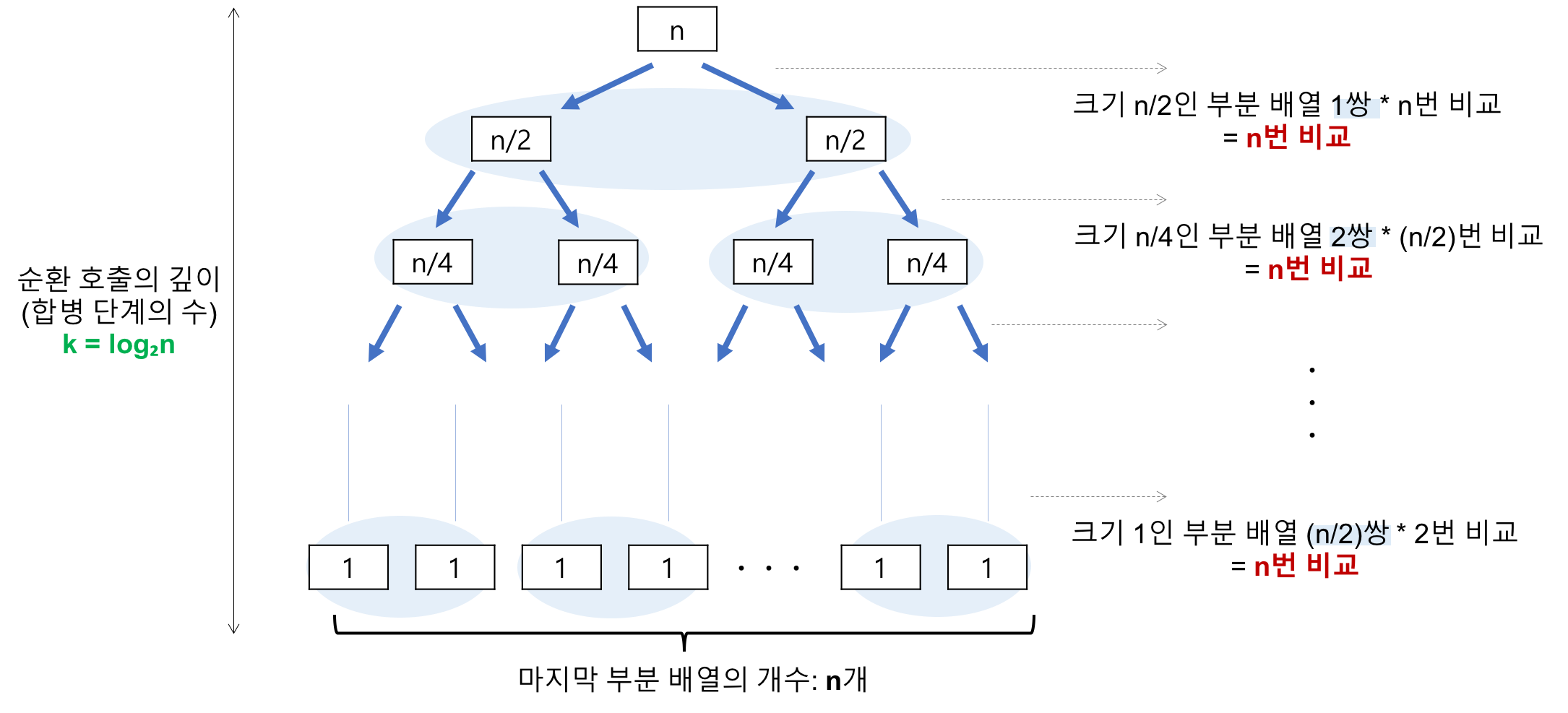
순환 호출의 깊이(합병 단계의 수)

레코드의 개수가 n이라고 하고 2의 거듭제곱이라고 가정(n= $2^k$ )했을 때, $2^3$ → $2^2$ → $2^1$ → $2^0$ 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있을 것입니다. 이것을 일반화하면 $n=2^k$ 의 경우, $k = log_2n$ 임을 알 수 있다.

각 병합 단계의 비교 연산

크기 1인 부분 배열 2개를 합병하는데 최대 2번의 비교 연산이 필요하고, 부분 배열의 쌍이 4개 이므로 2 X 4 = 8번의 비교 연산이 필요하다. 다음 단계에서는 크기 2인 부분 배열 2개를 합병하는데 최대 4번의 비교 연산이 필요하고, 부분 배열의 쌍이 2개 이므로 4 X 2 = 8번의 비교 연산이 필요하다. 마지막 단계에서는 크기 4인 부분 배열 2개를 합병하는데 최대 8번의 비교 연산이 필요하고, 부분 배열의 쌍이 1개 이므로 8 X 1 = 8번의 비교 연산이 필요하다. 이것을 일반화하면 하나의 병합 단계에서는 최대 n번의 비교 연산을 수행함을 알 수 있습니다.

순환 호출의 깊이 만큼의 병합 단계 * 각 병합 단계의 비교 연산 = $nlog_2n$

이동 횟수

순환 호출의 깊이(병합 단계의 수)

$k = log_2n$
레코드를 배열(Array)로 구상하면, 임시 배열이 필요하다.
-> 제자리 정렬(in-place sorting)이 아니다.각 병합 단계의 이동 연산
임시 배열에 복사했다가 다시 가져와야 되므로 이동 연산은 총 부분 배열에 들어 있는 요소의 개수가 n인 경우, 레코드의 이동이 2 X n번 발생한다.