힙 정렬
힙 정렬이란?
힙 정렬(heap sort)는 힙(heap)을 사용하여 정렬하는 알고리즘입니다. 힙은 "부모의 값이 자식의 값보다 항상 크다(작다)"라는 조건을 만족하는 완전이진트리입니다.
자료구조 ‘힙(heap)’
- 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료 구조
- 최대 힙 혹은 최소 힙으로 구성
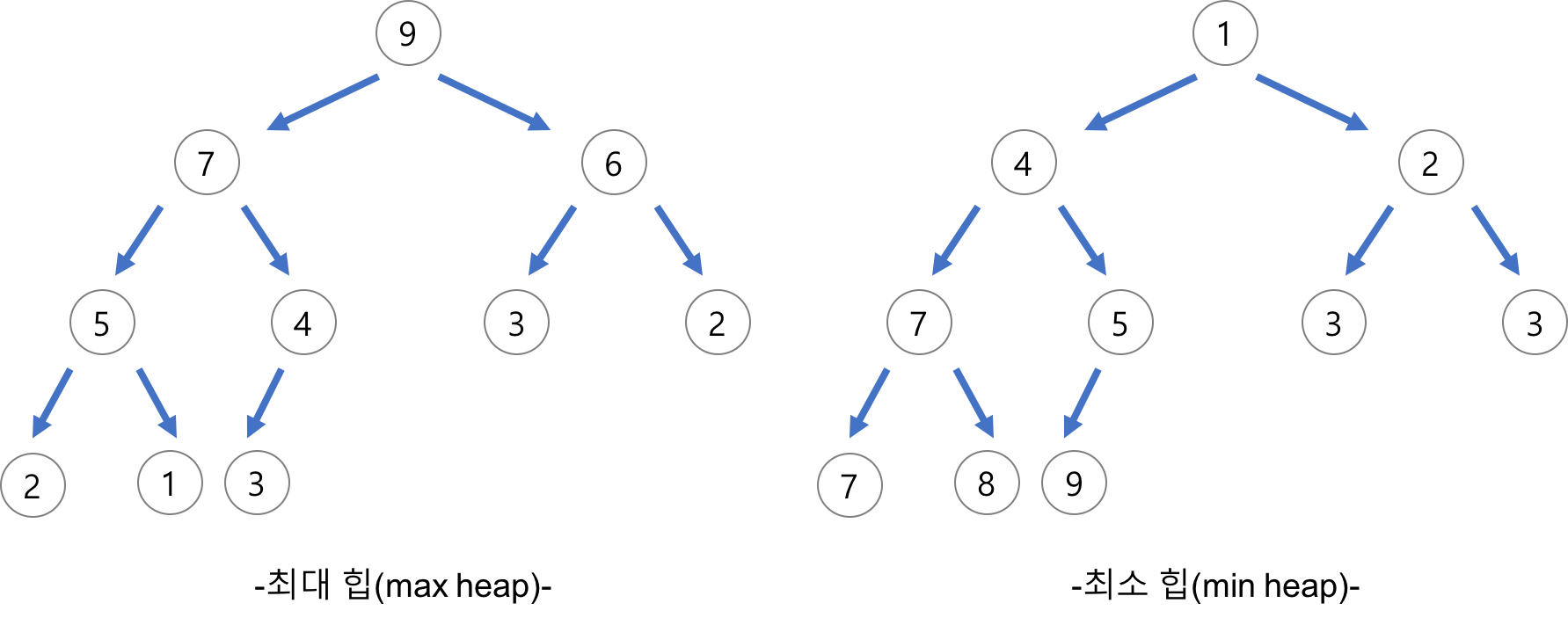
힙의 요소를 배열로 저장하면 부모와 자식의 인덱스 사이에 다음과 같은 관계가 성립합니다.
1.부모: a[(i - 1) / 2]
2. 왼쪽 자식: a[i * 2 + 1]
3. 오른쪽 자식: a[i * 2 + 2]
⚡ 여기서 TIP ⚡
왜 이런 관계 Index가 나오는 것일까요?
먼저 해당 Index 관계의 경우 트리의 시작 Index가 0부터 시작한다고 했을 경우에 이와 같은 관계가 나옵니다.
만약, Index가 1부터 시작하는 트리라면 다음과 같습니다.
- 부모: a[i / 2]
- 왼쪽 자식: a[i * 2]
- 오른쪽 자식: a[i * 2 + 1]
이것은 생각해보면 간단한데, 기존에 index가 0부터 시작할 경우 왼쪽 자식과 오른쪽 자식의 Index에 /2를 할 경우 오른쪽 자식은 +2가 있어서 +1이 남아버리게 됩니다.
따라서, 해당 경우에는 -1을 빼고 내서 /2를 해줘야 하는 것입니다.
반면에 Index가 1부터 시작하는 경우에 왼쪽 자식과 오른쪽 자식에 /2를 해줄 경우 + 되는 숫자가 남아 있지 않으므로 정확히 부모 Index를 구해낼 수 있습니다.
동작 과정
- 정렬할 배열을 최대 힙 구조로 만든다.
- 최대 힙에서 루트(최대값)를 꺼내 배열의 가장 마지막 요소와 교환한다.
- 교환한 후, 최대 힙의 크기를 1 줄이고(루트 노드를 제거했으므로), 루트 노드부터 다시 최대 힙을 구성한다.
- 2, 3번을 반복한다. 이때, 최대 힙의 크기가 1이 될 때까지 반복한다.
- 반복문이 종료되면 정렬이 완료된다.
장단점
장점
- 시간 복잡도가 좋은편이다.
- 추가적인 배열이 필요하지 않다.(in-place algorithm, 병합 정렬보다 효율적)
- 힙 정렬이 가장 유효한 경우는 전체 자료를 정렬하는 것이 아니라 가장 큰 몇개만 필요할 때이다.
단점
- 데이터의 상태에 따라 같은 시간 복잡도라도 조금 느리다.
- 일반적으로 속도만 비교하자면 퀵이 평균적으로 더 빠르다. 그래서 잘 사용하지 않는다.
- 불안정 정렬이다.
코드
void swap(int[] a, int idx1, int idx2) {
int tmp = a[idx1]; a[idx1] = a[idx2]; a[idx2] = a[idx1];
}
// a[left] ~ a[right]를 힙으로 만든다.
void downHeap(int[] a, int left, int right){
int temp = a[left]; // 루트 노드
int parent;
int child;
for(parent = left; parent < (right + 1) / 2; parent = child) {
int cl = parent * 2 + 1; // 왼쪽 자식
int cr = cl + 1; // 오른쪽 자식
child = (cr <= right && a[cr] > a[cl]) ? cr : cl; // 큰 값을 가진 노드를 자식에 대입
if(temp >= a[child]) break;
else
a[parent] = a[child];
}
// 최종 종착지에서만 값 수정
a[parent] = temp;
}
// 힙 정렬
void heapSort(int[]a) {
int n = a.length;
// a[0] ~ a[n-1] 힙정렬 => 부모 노드인 부분부터 반복문 실행
for(int i = (n - 1) / 2; i >= 0; i--) // a[i] ~ a[n-1]를 힙으로 만들기
downHeap(a, i, n - 1);
for(int i = n - 1; i > 0; i--) {
swap(a, 0, i); // 가장 큰 요소와 아직 정렬되지 않은 부분의 마지막 요소를 교환
downHeap(a, 0, i - 1); // a[0] ~ a[i-1]를 힙으로 만듭니다.
}
}몇 부분만 살펴보자.
먼저, 반복문에서 아래 조건식이 왜 저렇게 나왔는지 확인해보자.
for(parent = left; parent < (right + 1) / 2; parent = child) {해당 코드의 경우 left Node를 root로 가지는 서브 트리를 최대 힙 트리로 만들어 주는 과정이라고 생각하면 된다. 현재 해당 트리의 경우 마지막 부모 노드의 인덱스 값이 (right - 1) / 2 이다. 거기다가 + 1만큼 더하면 마지막 부모 노드의 다음 노드 인덱스 값이 구해진다. 따라서 (right + 1) / 2가 나온 것이다.
child = (cr <= right && a[cr] > a[cl]) ? cr : cl;해당 코드도 주의 해줘야 하는데 만약 아래와 같이 코드를 짜면 어떻게 될 것인가?
child = (cr <= right && a[cl] > a[cr]) ? cl : cr;해당 식은 위의 식과 매우 다른 결과를 도출해 낸다. 왜냐하면, 앞의 조건 때문이다. 만약, cr이 right보다 크다면 Index의 범위를 넘어섰고, 그때의 결과값으로 나와야 하는 것은 존재하지 않는 cr이 아닌 cl을 결과 값으로 child에 넣어줘야 할 것이다. 하지만 아래의 코드는 삼항연산자에서 거짓일때의 결과값에 cr이 위치하고 있어서 틀린 코드이다.
시간 복잡도
시간복잡도를 계산한다면,
- 힙 트리의 전체 높이는 (완전 이진 트리)이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 만큼 소요된다.
- 요소의 개수가 n개 이므로 전체적으로 의 시간이 걸린다.
Reference
