Scheduling

• Scheduling: 실행 시간이 서로 다른 Job들을 실행할 때 'Time in the System'을 최소화 하는 Job 실행 순서를 정하는 것

  • Time in the System: Job이 실행될 때 까지의 대기 시간과 Job의 실행 시간의 합
  • 과거에 Disk Scheduling, Elevator Scheduling 등에 사용
    → Starvation 발생

• Scheduling With Deadlines: 각 Job들의 실행 시간은 동일하나 Profit과 Deadline이 다양할 때 Profit을 최대로 하는 Job 실행 순서를 정하는 것

Minimizing Total Time in the System

• 세 개의 Job이 다음과 같을 때
  $t₁ = 5       t₂ = 10      t₃ = 4$

  • $t₁, t₂, t₃$ 의 순서로 실행이 된다고 가정하면
    Time in the System: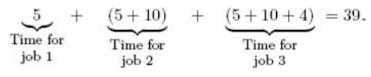

    

  • 가능한 Job Schedule & Time in the System:

    • [1, 2, 3] = 5 + (5 + 10) + (5 + 10 + 4) = 39
    • [1, 2, 3] = 5 + (5 + 10) + (5 + 10 + 4) = 39
    • [1, 2, 3] = 5 + (5 + 10) + (5 + 10 + 4) = 39
    • [1, 2, 3] = 5 + (5 + 10) + (5 + 10 + 4) = 39
    • [1, 2, 3] = 5 + (5 + 10) + (5 + 10 + 4) = 39
    • [1, 2, 3] = 5 + (5 + 10) + (5 + 10 + 4) = 39

• Optimal Solution은 가장 짧은 Job부터 순서대로 실행하는 것

Scheduling with Deadlines

• Scheduling with Deadlines
  • 각 Job의 실행 시간은 동일하나 Profit은 모두 다른 경우
  • 각 Job이 Deadline 이전 혹은 Deadline 시점에 실행을 시작하면 Profit을 달성한다고 정의
  • 가장 많은 Profit을 만족하는 Scheduling을 의미 (단, 모든 Job을 실행할 필요는 없음)

Example 1

Job      Deadline     Profit
 1           2          30
 2           1          35
 3           2          25
 4           1          40

가능한 Job Schedule & Profit
Schedule            Profit
  [1, 3]          30 + 25 = 55
  [2, 1]          35 + 30 = 65
  [2, 3]          35 + 25 = 60
  [3, 1]          25 + 30 = 55
  [4, 1]          40 + 30 = 70 → Maximum Profit
  [4, 3]          40 + 25 = 65

모든 경우의 수 고려 시 $T(n) = θ(n!)$

• Algorithm
  • Job을 Profit에 대한 Decreasing Order로 정렬
  • 각 Job이 Scheduling 가능한지 순서대로 확인 (Deadline과 경과 시간 비교)
• Definitions
  • Feasible Sequence: Sequence 내의 모든 Job이 Deadline 이전에 실행 가능할 때
  • Feasible Set: Job의 집합에서 최소 하나 이상의 Feasible Sequence가 존재할 때
    • 위의 Example 1에서 [4, 1]은 Feasible Sequence이므로 {1, 4} = Feasible Set
  • S의 Job을 Deadline의 Nondecreasing Order로 정렬한 Sequence가 Feasible이면 S는 Feasible이다.

Example 2

Job      Deadline     Profit
 1          3           40
 2          1           35
 3          1           30
 4          3           25
 5          1           20
 6          3           15
 7          2           10

① S = Ø
② [1] = Feasible → S = {1}
③ [2, 1] = Feasible → S = {1, 2}
④ 1, 2, 3이 모두 속하는 Feasible Sequence는 존재하지 않는다.
⑤ [2, 1, 4] = Feasible → S = {1, 2, 4}
⑥ 1, 2, 4, 5가 모두 속하는 Feasible Sequence는 존재하지 않는다.
⑦ 1, 2, 4, 6이 모두 속하는 Feasible Sequence는 존재하지 않는다.
⑧ 1, 2, 4, 7이 모두 속하는 Feasible Sequence는 존재하지 않는다.
→ Feasible Set : {1, 2, 4}

Huffman Code

• Data를 적절한 방법으로 Encoding하면 저장하는데 필요한 Memory 절약 가능 → Data Compression

• Defiitions

  • Binary Code: 컴퓨터에서 Data를 표현하는 가장 일반적인 방법
  • Codeword: 각 Character를 표현하는 Binary Code
  • Fixed-Length Binary Code: 길이가 일정한 Binary Code
  • Variable-Length Binary Code: Character별로 길이가 각각 다른 Binary Code

• Huffman Encoding

  • Data Compression을 위한 Encoding 방법 중 하나
  • 파일 상에 존재하는 빈도에 따라 Data를 표현하는 Code의 길이를 다르게 정의
    Fixed-Length Binary Code → Variable-Length Binary Code

• 표현해야 할 데이터가 ababcbbbc일 때

  • a: 00, b: 01, C: 11로 정의
    → 000100011101010111로 표현

  • a: 10, b: 0, c: 11로 정의
    → 1001001100011로 표현 (Huffman Code)
    a: 1로 정의하면 1로 시작하는 코드가 나왔을 때 a인지 다른 코드의 시작인지 구분할 수 없다.

• Optimal Binary Code Problem: 파일의 길이를 최소로 하는 Character Code를 찾는 것

• Prefix Code: 한 Character의 Code Word가 다른 Character의 Code Word의 시작을 구성하지 않는 것

  • 예를 들어 a의 Code Word가 01이라면 b의 Code Word는 011이 될 수 없다.
  • Fixed-Length Code는 Prefix Code
  • Parsing: Tree의 Root에서 시작해서 Leaf Node를 만나면 Code 완료
  • 장점: File을 Parsing할 때 확인할 필요 X

• Character Set과 Frequency가 다음과 같을 때

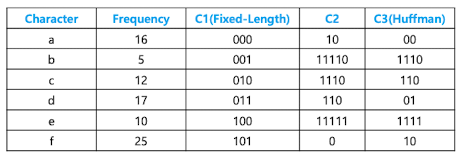
• Code C1, C2, C3을 사용한 파일 크기
  Bits(C1) = 16(3) + 5(3) + 12(3) + 17(3) + 10(3) + 25(3) = 255
  Bits(C2) = 16(2) + 5(5) + 12(4) + 17(3) + 10(5) + 25(1) = 231
  Bits(C3) = 16(2) + 5(4) + 12(3) + 17(2) + 10(4) + 25(2) = 212 → Huffman Code
• Binary Character Code의 Tree 표현

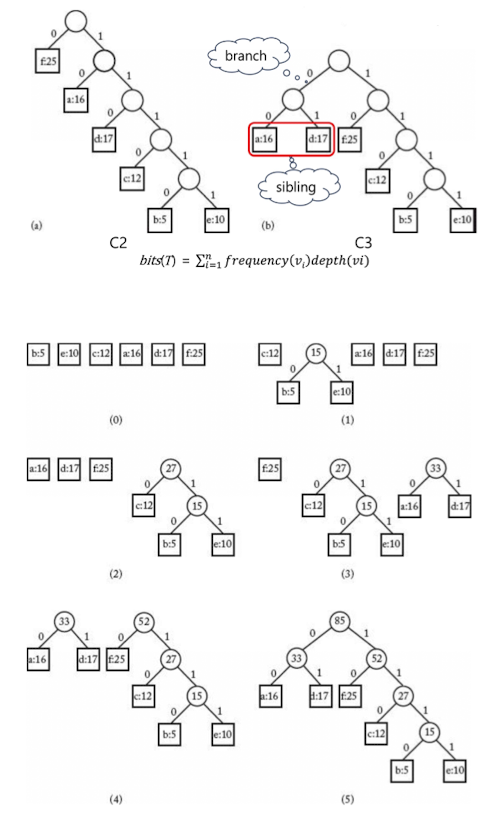
Greedy VS Dynamic

• Optimization Problem
  • Greedy Approach와 Dynamic Programming을 사용
  • 하나의 문제를 두 가지 방법으로 모두 해결할 수 있는 경우 존재
  • Greedy Approach를 사용할 때는 반드시 Optimal Solution을 생성하는지 증명
  • Dynamic Programming은 Principal of Optimality 증명

Knapsack Problem

• 크기가 W인 Knapsack에 최대한 많은 Item을 넣는 방법을 찾는 문제
  • 0-1 Knapsack: Greedy Approach 사용 불가
  • Fractional Knapsack: Greedy Approach 사용 가능

0-1 Knapsack

• 0-1 Knapsack Problem

  • 도둑이 보석가게 침입(Max, Weight가 W인 Knapsack 소지)
  • 보석은 무게(W)와 가격(P)이 각각 상이
  • Profit을 최대로 하고 Weight의 합이 W를 넘지 않는 보석의 집합(A)을 구하는 것이 목표

  

  $S$ = {$item₁$, $item₂$, ··· , $itemₙ$}
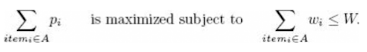
  $wᵢ$ = Weight of $itemᵢ$
  $pᵢ$ = Profit of $itemᵢ$
  $W$ = Maximum Weight

  Brute-Force Algorithm 사용 시: $O(2^n)$

• Greedy Approach

1. Profit이 큰 순으로 정렬 후 Greedy 시도 → Profit이 큰 Item이 무게도 무겁다면?
2. 무게가 가벼운 순으로 정렬 후 Greedy 시도 → 무게가 가볍지만 Profit도 작다면?
3. 'Profit / 무게'가 큰 순으로 정렬 후 Greedy

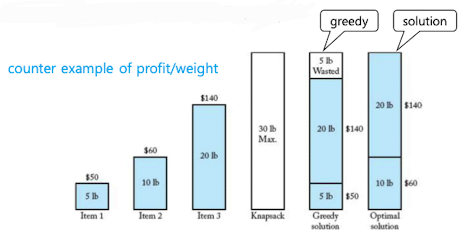
• Principal of Optimality가 성립하면 Dynamic Programming 적용 가능
  • A를 Item n에 대한 Optimal Subset이라고 가정
  • if itemₙ ∉ A이면, A는 n-1 Item에 대한 Optimal Solution과 같다.
  • else itemₙ ∈ A이면, A는 pₙ + n-1 Item에 대한 Optimal Solution과 같다.
  • P[i][w]: i번째 까지의 Item에서 무게 w를 넘지 않는 최대 Profit
    $P[i][w] = \begin{cases} maximum(P[i - 1][w], &pᵢ + P[i - 1][w - wᵢ])&if\;wᵢ≤w\\ P[i - 1][w],&if\;wᵢ>w \end{cases}$
    → $nW ∈ θ(nW)$
    

Fractional Knapsack

• Fractional Knapsack Problem
  • Knapsack에 원하는 용량(Fraction)을 쪼개 담을 수 있음
  • 'Profit / 무게'가 큰 순으로 정렬 후 Greedy
    → Optimal Solution 가능