알고리즘 - Divide and Conquer

분할 정복. 사실 이 개념도 자료구조에서 다뤘었지만, 복습 차원에서 다시 살펴보자.

• Algorithm
  • 입력을 2개 또는 그 이상의 작은 입력으로 분리
  • 나누어진 입력이 쉽게 처리될 수 있는 크기면 처리, 그렇지 않으면 다시 분리
  • 필요시, 처리된 각각의 작은 입력값을 결합하여 하나의 결과 생성
    ⠀⠀
• Merge Sort에서의 Divide and Conquer 예시
  

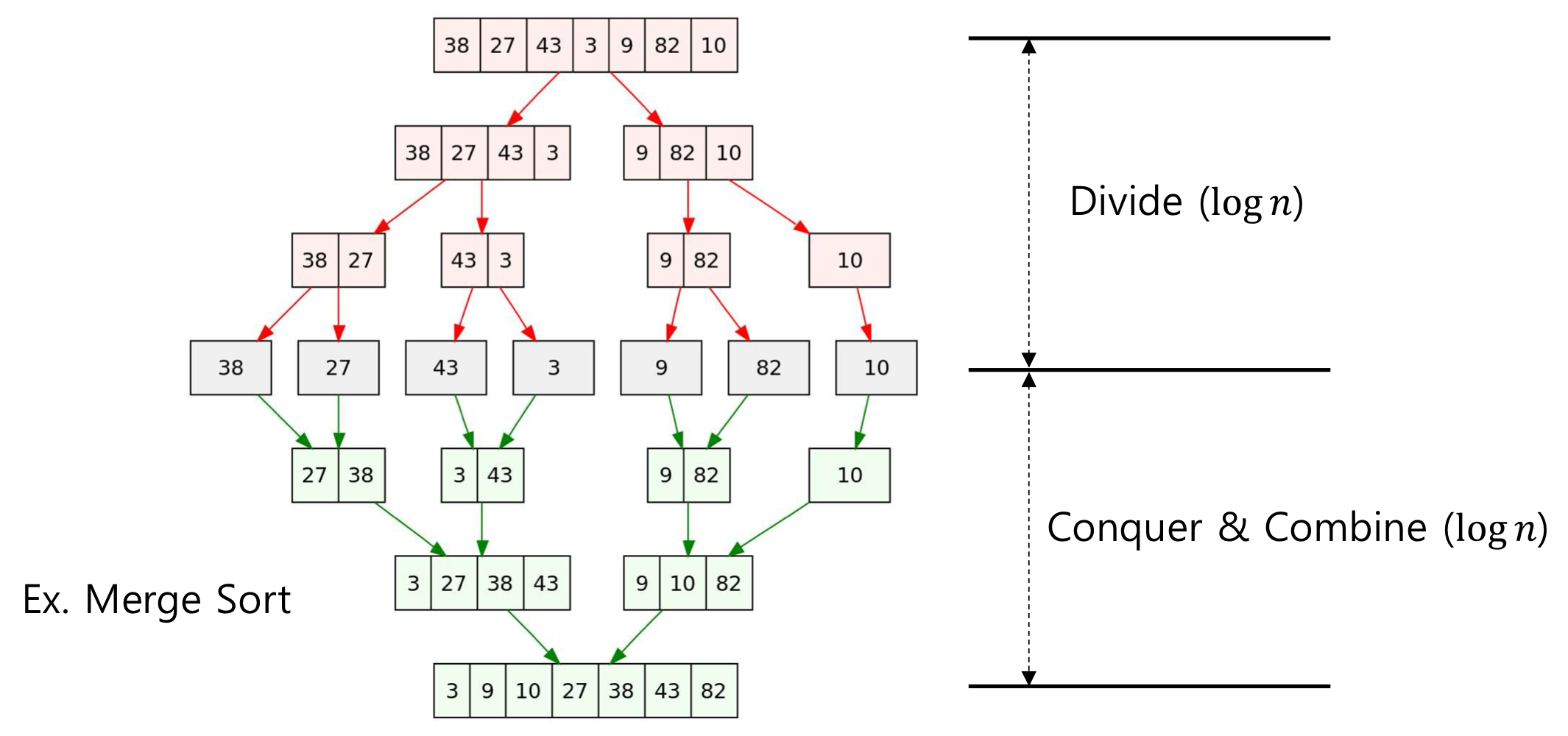
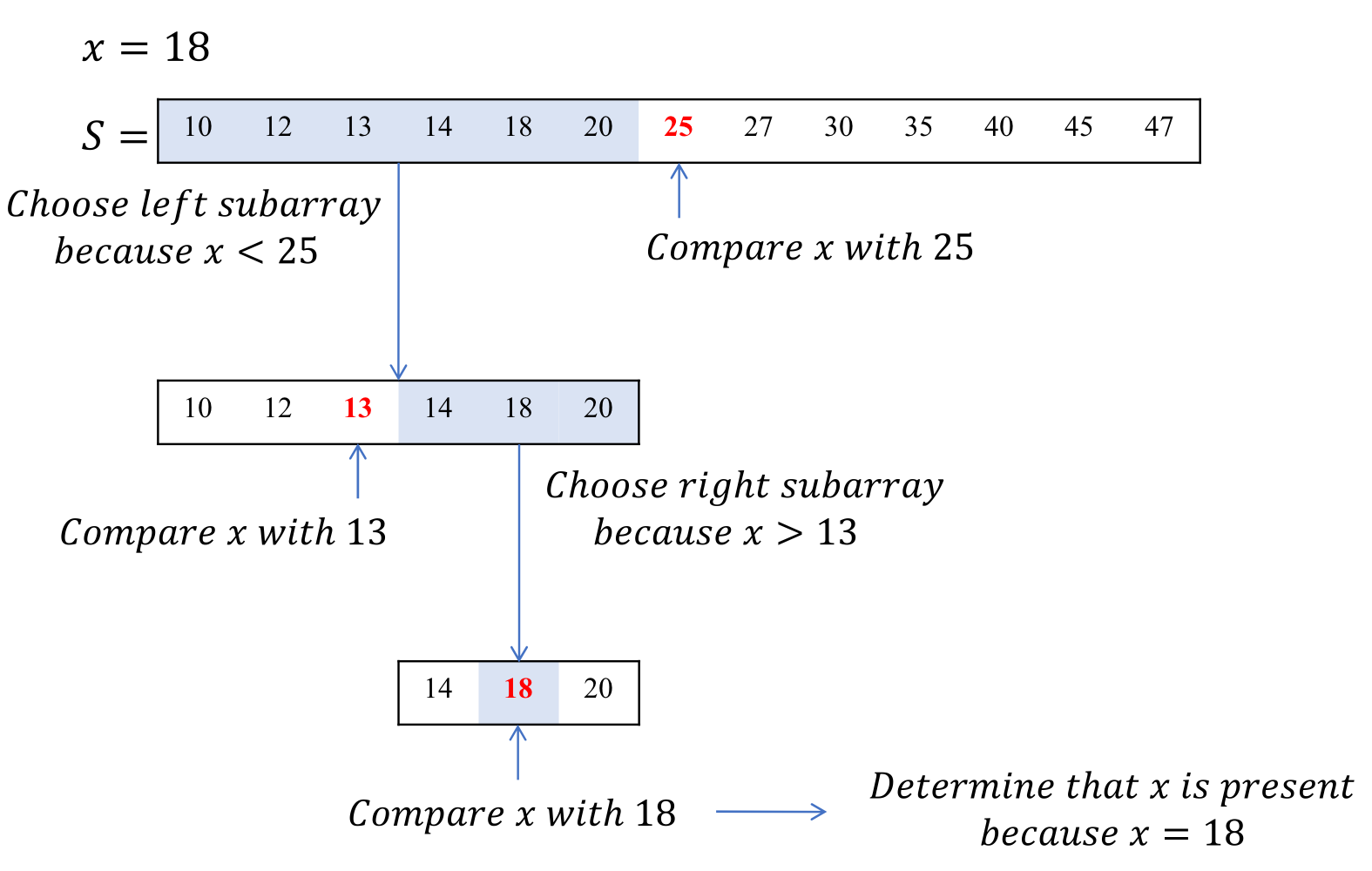
Binary Search

• 가장 단순한 형태의 Divide and Conquer
  • Combine 과정이 없다.
  • Sub Instance의 결과값 == Original Instance의 결과값
    ⠀⠀
• Recursive Binary Search 구현
  • 실행되는 동안 값이 변하지 않는 변수는 Parameter로 사용할 필요가 없다.
    • Recursive 함수의 구조가 단순해진다.
    • 함수 호출 시 발생하는 Memory 복사를 줄여 Stack 공간을 절약할 수 있다.

Recursion 구분

• Tail-Recursion
  • Recursive 함수 호출 후 추가 처리없이 Return하는 Recursion
  • Iterative 형태로 변형이 용이하다.
    ⠀⠀
• Recursive Implementation vs Iterative Implementation
  • Recursive Implementation의 속도가 더 느리다.
    • 함수 호출 시/종료 시 Stack을 사용하는데 이때 Memory Read/Write 발생
  • Recursive Implementation의 Memory 사용이 많다.
    • 함수 호출 시 Parameter와 Return Address를 저장하기 위해 Stack Memory 사용

Worst-Case Time Complexity

• Basic Operation: S[mid]와 x를 비교하는 Operation
• Input Size: $n$(배열에 저장된 Item의 개수)
• Worst-Case: x가 배열에 존재하지 않을 때

Code

int location(int S[], int low, int high) {
	int mid = (low + high) / 2;

	if (low > high)
		return -1;
	else {
		if (S[mid] == x)
			return mid;
		else if (S[mid] < x)
			return location(S, mid + 1, high);
		else
			return location(S, low, mid - 1);
	}
}

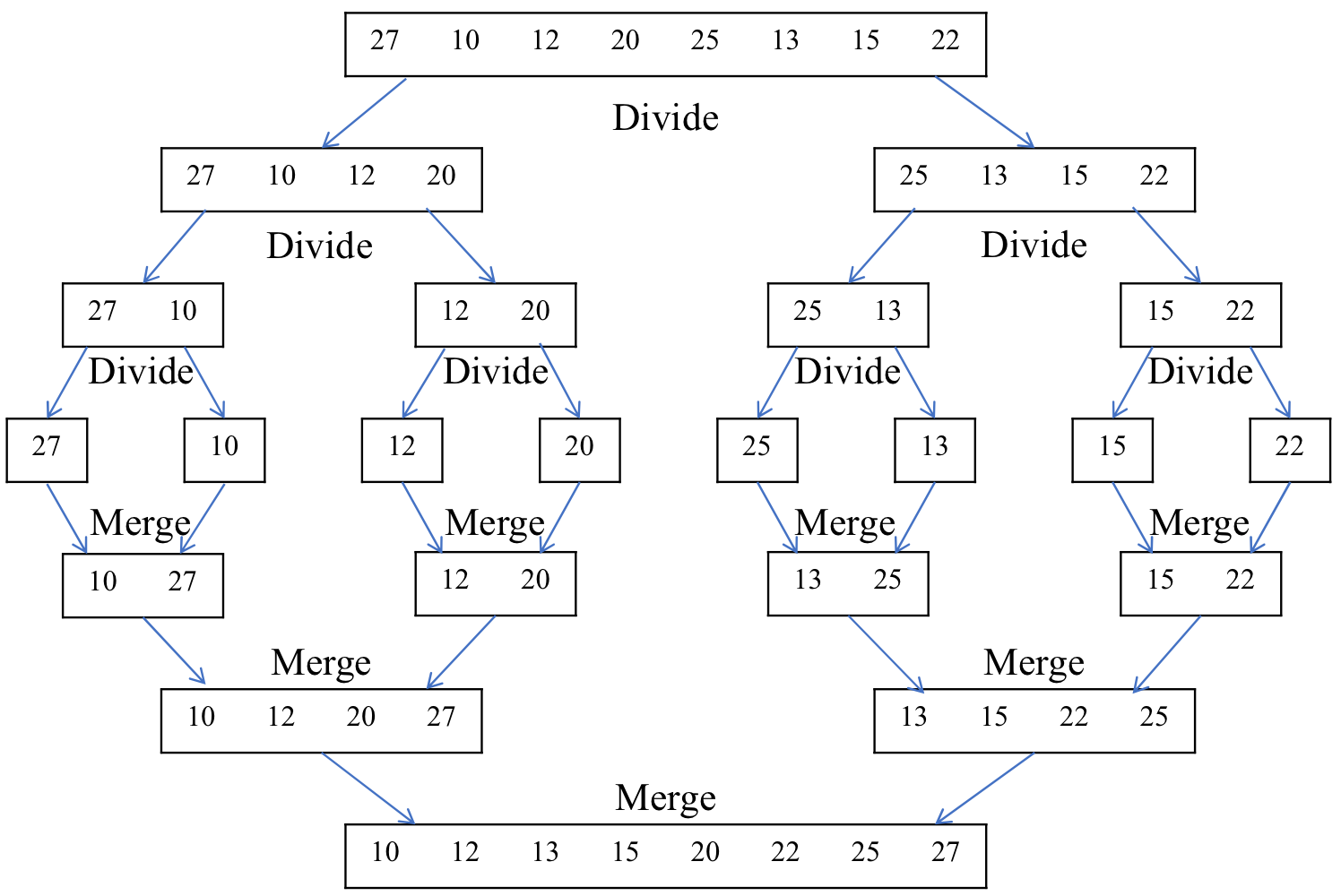
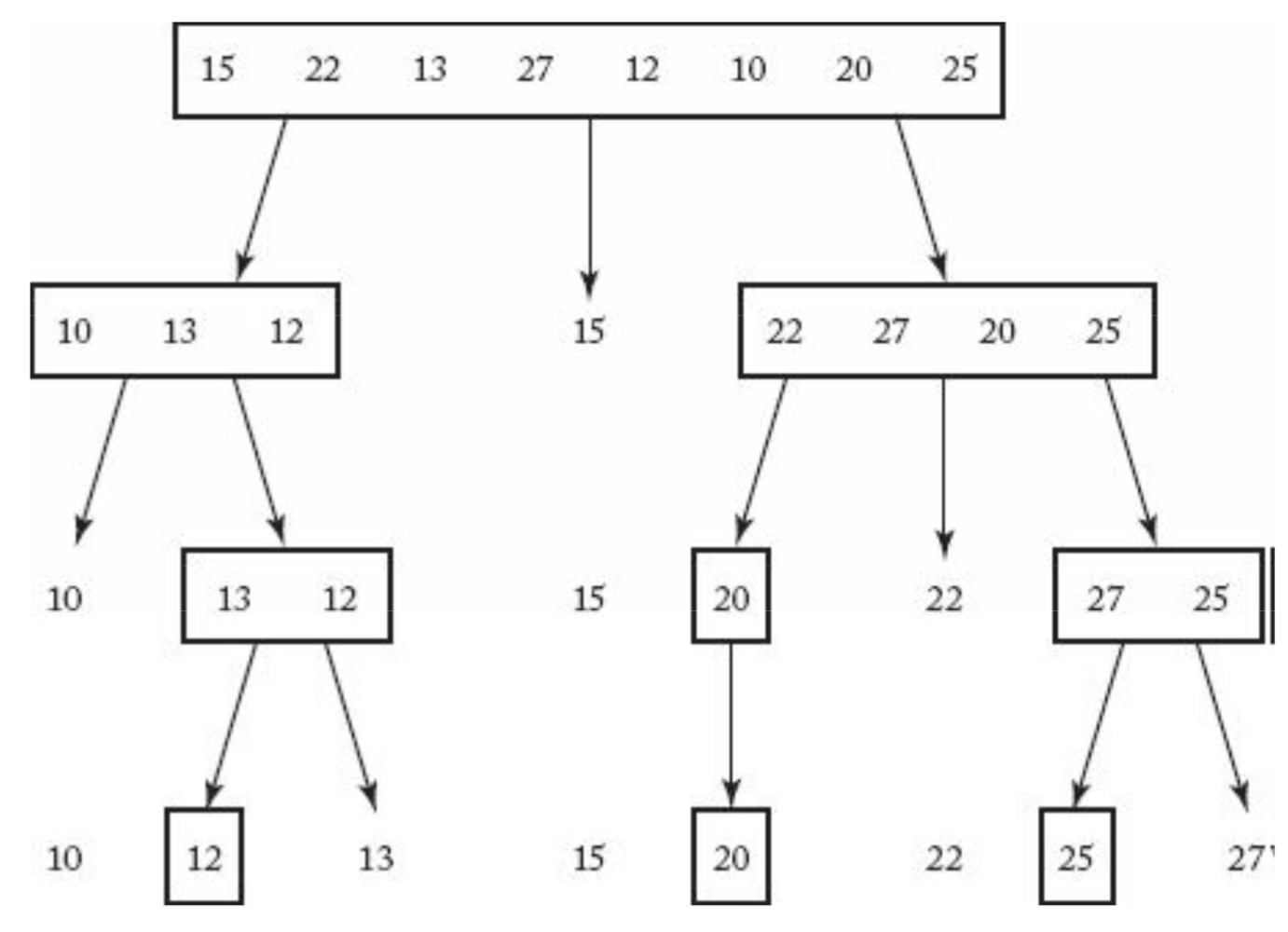
Merge Sort

• Sorting된 두 개의 배열을 Merge하여 하나의 Sorting된 배열로 만든다.
• Input: 길이가 $h$인 배열 U, 길이가 $m$인 배열 V
• Output: 길이가 $h + m$인 배열 S
  

Worst-Case Time Complexity (Merge)

• Basic Operation: U[i], V[j]를 비교하는 Operation
• Input Size: $h + m$
• Worst-Case: $i = h + 1$, $j = m$일 때

Worst-Case Time Complexity (Merge Sort)

• Basic Operation: Merge에 존재하는 비교 연산
• Input Size: $n$(배열에 저장된 원소의 개수)
• Worst-Case: $h + m = n$, $i = h + 1$, $j = m$일 때

Code

while (i < lenA && j < lenB) {
	if (A[i] < B[j])
		C[k++] = A[i++];
	else
		C[k++] = B[j++];
}

while (i < lenA)
	C[k++] = A[i++];

while(j < lenB)
	C[k++] = B[j++];

Quick Sort

• Complexity
  • Average-Case Complexity: $n log$ $n$
  • Worst-Case Complexity: $n^2$
• In-Place Sort
• Pivot 사용
  • 배열을 Pivot보다 작은 값과 큰 값을 갖는 두 개의 배열로 분리
  • Pivot은 배열의 제일 앞 또는 제일 뒤에 위치한 값을 사용

Every-Case Time Complexity (Partition)

• Basic Operation: S[i]와 Pivot의 비교 횟수
• Input Size: Subarray의 원소 개수

Worst-Case Time Complexity (Quick Sort)

• Basic Operation: Partion 함수에서 S[i]와 Pivot의 비교 횟수
• Input Size: 배열 내 원소의 개수($n$)
• Worst-Case
  • 입력 배열의 값이 이미 정렬되어 있을 때
  • 길이 n의 배열이 길이 1, 길이 $n-1$의 두 개 배열로 분리될 때

Average-Case Time Complexity (Quick Sort)

• Basic Operation: Partition 함수에서 S[i]와 Pivot의 비교 횟수
• Input Size: 배열 내 원소의 개수($n$)

Matrix Multiplication

• Matrix Multiplication Time Complexity
  • $T(n) = n^3$
  • $n = 2$일 때 곱셈 8번, 덧셈 4번
    ⠀⠀
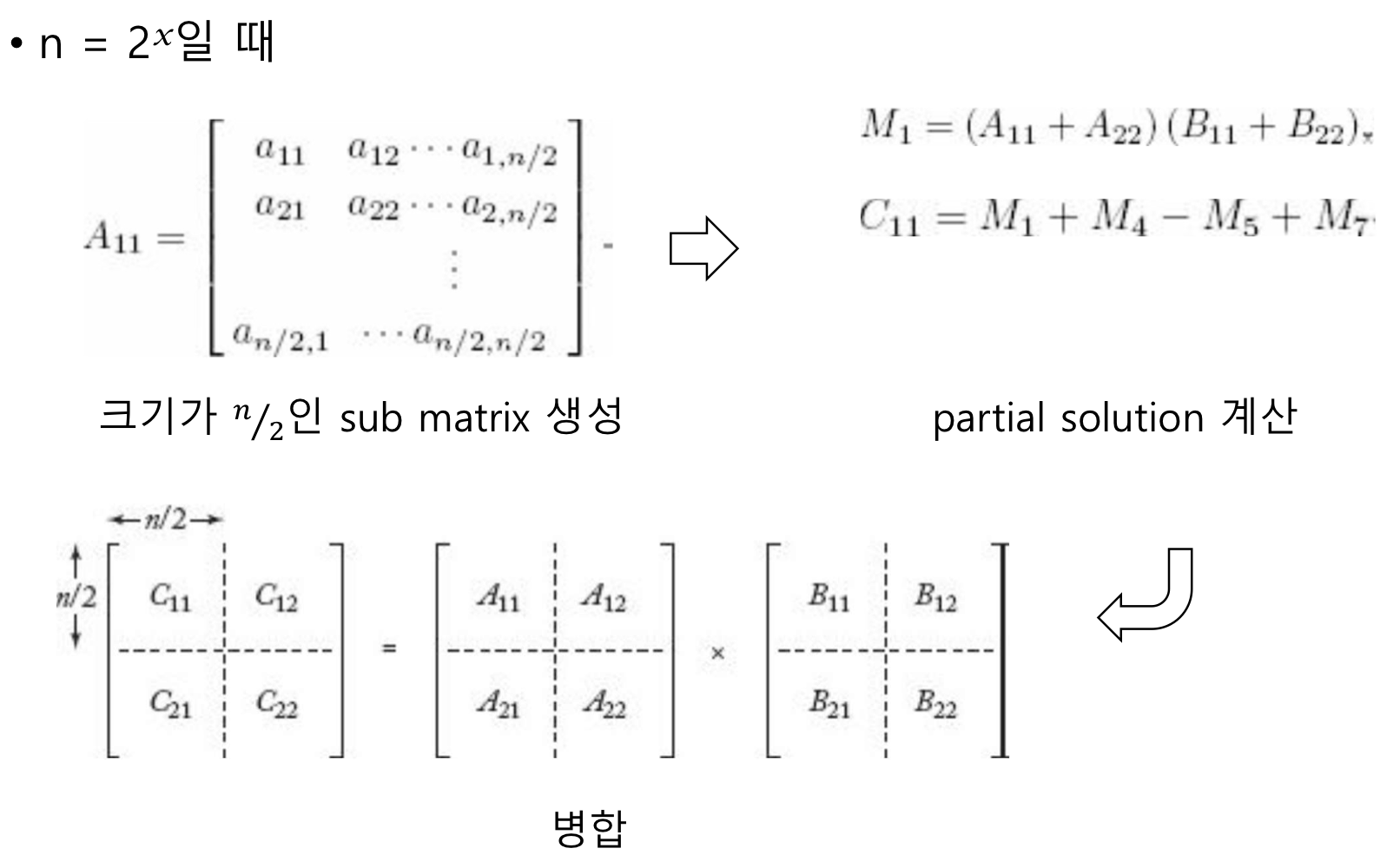
• 1969년 Strassen의 개선된 알고리즘
  • $T(n) = n^2$$^.$$^8$$^1$
  • $n = 2$일 때 곱셈 7번, 덧셈/뺄셈 18번
  • $n$이 큰 경우 성능 차이 심화

Every-Case Time Complexity (Matrix Multiplication)

• Multiplication
  • Basic Operation: 곱셈
  • Input Size: Matrix의 Row와 Column의 수($n$)
  • Complexity
    • $n / 2$ 크기의 Matrix를 계산할 때 곱셈 7회 수행
    • $n = 1$일 때 곱셈 1회 수행
• Addition
  • Basic Operation: 덧셈
  • Input Size: Matrix의 Row와 Column의 수($n$)
  • Complexity
    • $n / 2$ 크기의 Matrix Strassen 함수를 7회 호출, 한 번 호출 시 덧셈 18회 수행
    • $n = 1$일 때 덧셈 0회 수행

Large Integers

• Computer Hardware의 한계를 초과하는 큰 수의 처리 필요시
  • Sofrware로 접근하여 처리 (ex. 정수의 배열로 수를 표현)
  • Divide and Conquer 사용

ex) 큰 수의 곱셈

Worst-Case Time Complexity

• Basic Operation: Large Integer 연산 횟수
• Input Size: $n$, Large Integer의 자리수

Determining Thresholds

• 프로그램 동작시 발생하는 Overhead 때문에 $n$이 특정 개수 이하인 경우 $θ(nlog$ $n)$이 $θ(n^2)$보다 느린 경우가 발생
• $n$ 값은 Algorithm 구조와 Computer 구조에 영향을 받음
• Divide and Conquer Algorithm 사용 시 Threshold보다 작은 $n$에 대해서 다른 Algorithm을 적용하면 실행 속도를 높일 수 있음 (ex. Merge Sort + Exchange Sort)

When Not to Use Divide and Conquer

• Divide and Conquer 사용이 적절하지 않은 경우
  • $n$개의 입력이 '2개 또는 그 이상'의 $n$과 유사한 개수의 입력으로 분리될 때
  • $n$개의 입력이 $n/c$개의 $n$과 유사한 개수의 입력으로 분리될 때
  • Recursive Call에서 동일한 $n$을 반복 호출하는 경우 (ex. Fibonacci Recursion)