Dynamic Programming

• Divide and Conquer와 마찬가지로 문제의 Instance를 작게 분리
• 작은 Instance부터 Bottom-Up 형태로 계산한 결과를 배열(또는 테이블)에 저장하고 상위 Instance 계산 시 사용
• Divide and Conquer를 사용할 때, 분해된 Sub Instance 간에 상호 관련이 있을 경우 비효율적이라는 단점 보완 가능
• Recursive Property가 존재하면 Divide and Conquer와 Dynamic Programming은 유사
• Iterative한 형태로 해결 가능하다면 Divide and Conquer보다는 Dynamic Programming이 효율적이다.

Binomial Coefficient

• $n$개의 요소에서 $k$개를 선택할 수 있는 경우의 수

⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀↓

위 식은 $n!$ 또는 $k!$ 값을 계산할 필요가 없어서 Recursive Property로 사용하기 적절하다.

$(x+y)^3 = (x+y)(x+y)(x+y) = x^3 + 3x^2y + 3xy^2 + y^3$ 일 때,

$\begin{pmatrix}3\\2\\ \end{pmatrix} = \begin{pmatrix}2\\1\\ \end{pmatrix} +\begin{pmatrix}2\\2\\ \end{pmatrix}$ 에서 $\begin{pmatrix}2\\1\\ \end{pmatrix}$은 첫 번째 괄호에서 $x$를 선택한 경우이고, $\begin{pmatrix}2\\2\\ \end{pmatrix}$은 첫 번째 괄호에서 $x$를 선택하지 않은 경우이다.

Code without Dynamic Programming

int bin(int n, int k) {
	if (k == 0 || n == k)
    	return 1;
    else
    	return bin(n - 1, k - 1) + bin(n - 1, k);
}

아직 Dynamic Programming이 적용되지 않아 $\begin{pmatrix}n\\k\\ \end{pmatrix}$값을 얻기 위해 $2\begin{pmatrix}n\\k\\ \end{pmatrix}-1$ 번 계산해야 하는 비효율적인 알고리즘이 구현된다. 그리고 bin(n - 1, k - 1), bin(n - 1, k)는 모두 bin(n - 2, k - 1)을 호출해야 하는 반복 호출이 발생한다.

Code with Dynamic Programming

int bin2(int n, int k) {
	int table[n + 1][k + 1];
    
    for (int i = 0; i <= n; i++)
    	for (int j = 0; j <= min(i, k); j++)
			if (j == 0 || j == i)
		    	arr[i][j] = 1;
    		else
	    		arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j];
	return arr[n][k];
}

Time Complexity

• Input Size는 $n$, $k$가 아닌 $n$, $k$를 표현하는 비트 수이지만 $n$, $k$에 따른 Complexity를 계산하기 위해 이를 사용한다.
  

Floyd's Algorithm

Shortest Path

Graph 상의 한 노드에서 다른 노드로 가는 가장 짧은 경로. 경로는 Weighted Graph로 표현.

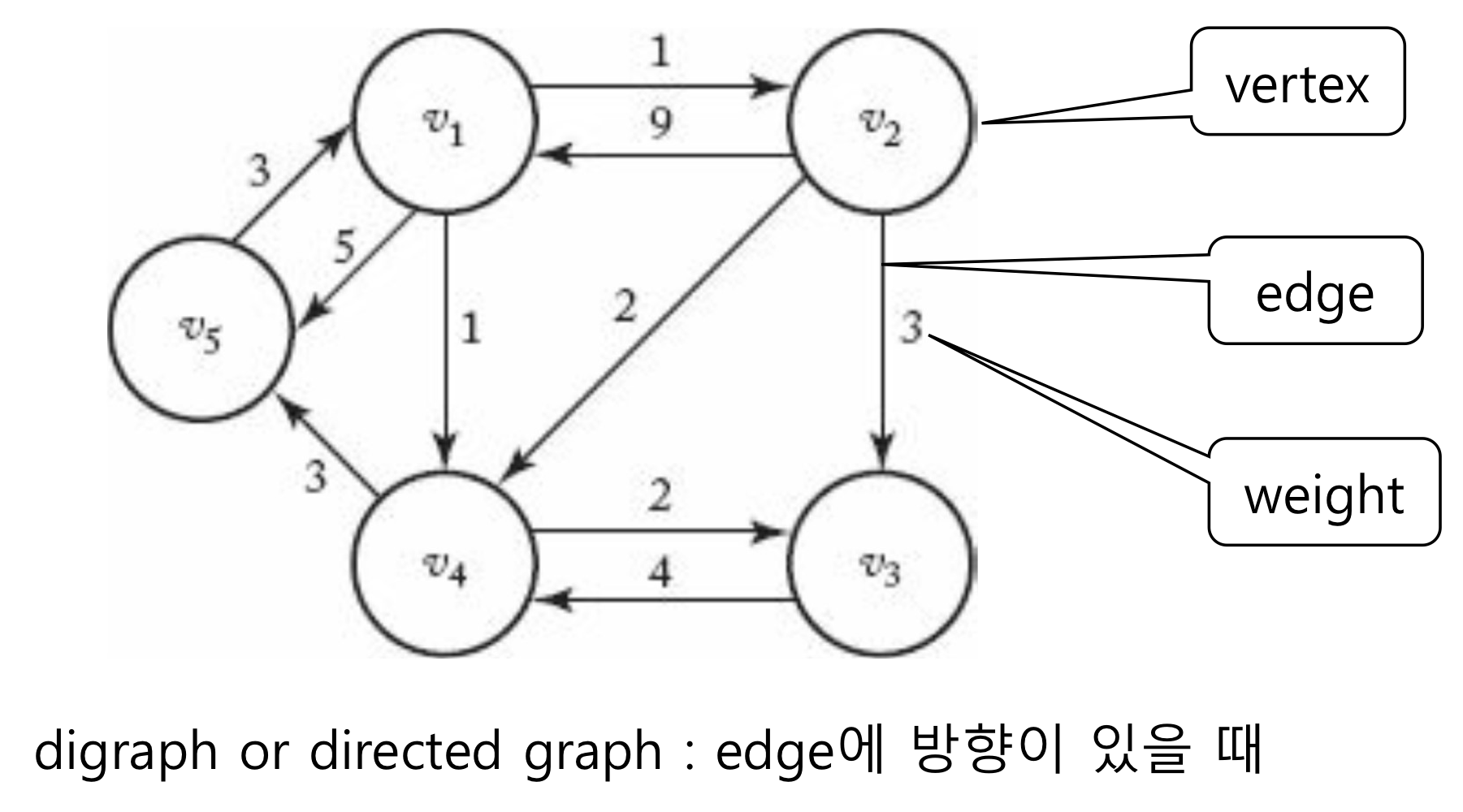
• 모든 경우의 수를 계산해서 최적의 해를 선택하는 방법의 Complexity (모든 Vertex가 Edge로 연결된 경우)
  • 첫 번째 Vertex가 두 번째 Vertex로 가는 Edge는 $n-2$ 개
  • 두 번째 Vertex가 세 번째 Vertex로 가는 Edge는 $n-3$ 개
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀.
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀.
    ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀.
    $(n-2)(n-3)···1 = (n-2)!$ ⠀⠀⮕⠀⠀Worse than Exponential

Algorithm

• Edge의 Weight를 2차원 Array로 표현

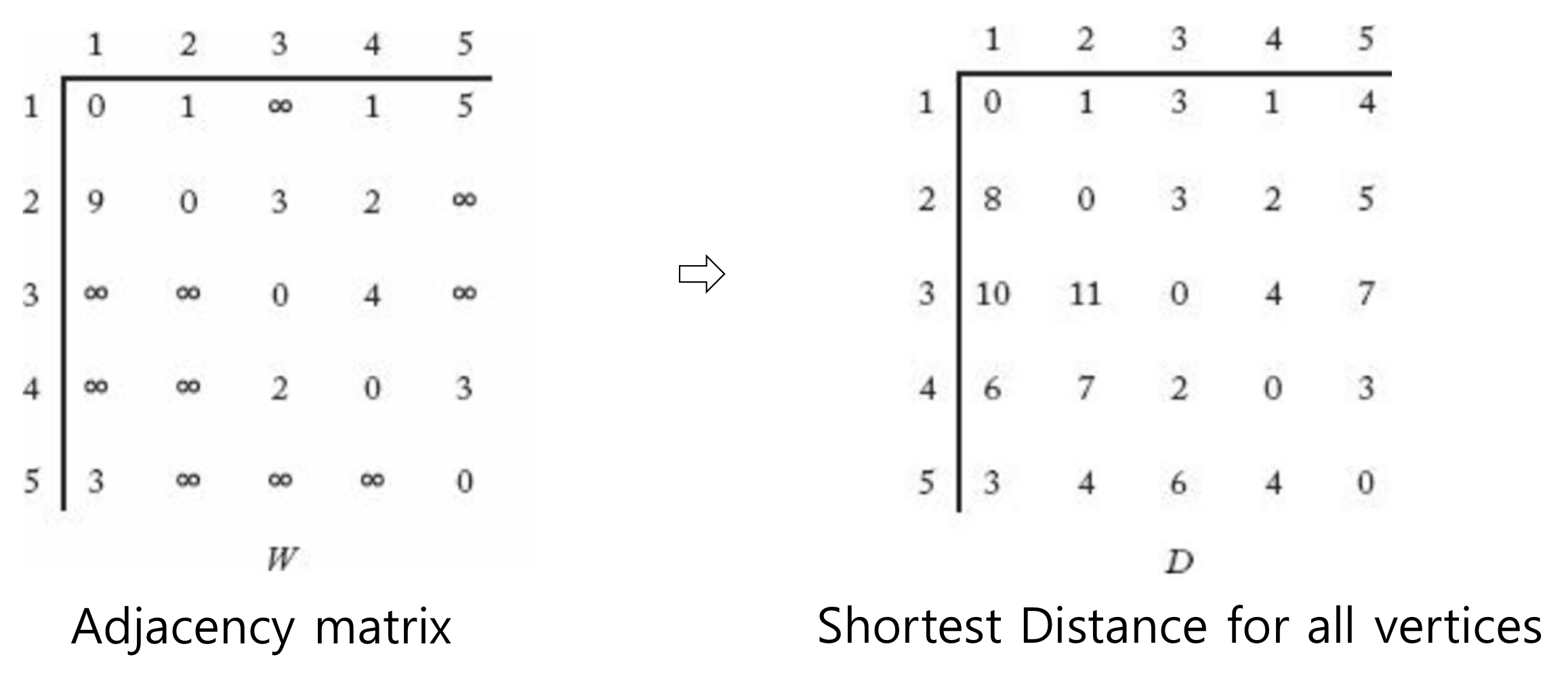
• $vᵢ$에서 $vⱼ$로의 Shortest Distance는 $vₖ$에 대해 다음 두 가지 경우가 존재 ($D^($$^k$$^)$$[i][j]$ : $vᵢ$에서 $vₖ$를 경유하여 $vⱼ$로 가는 Distance)

  • $vₖ$를 경유하지 않는 경우
    $D^($$^k$$^)$$[i][j]=D^($$^k$$^-$$^1$$^)$$[k][j]$
    ⠀⠀
  • $vₖ$를 경유하는 경우
    $D^($$^k$$^)$$[i][j]=D^($$^k$$^-$$^1$$^)$$[i][k]$ $+$ $D^($$^k$$^-$$^1$$^)$$[k][j]$

  ⮕ Shortest Distance

  $D^($$^k$$^)$$[i][j]=minimum(D^($$^k$$^-$$^1$$^)$$[i][j],$ $D^($$^k$$^-$$^1$$^)$$[i][k]$ $+$ $D^($$^k$$^-$$^1$$^)$$[k][j])$

Code without Shortest Path

void floyd(int n){
	for (int k = 1; k <= n; k++)
    	for (int i = 1; i <= n; i++)
        	for (int j = 1; j <= n; j++)
            	D[i][j] = minimum(D[i][j], D[i][k] + D[k][j]);
}

$T(n) = n * n * n = n^3 ∈ Θ(n^3)$

Code with Shortest Path

void floyd2(int n){
    for (int i = 1; i <= n; i++)
   		for (int j = 1; j <= n; j++)
            P[i][j] = 0;
            
	for (int k = 1; k <= n; k++)
    	for (int i = 1; i <= n; i++)
        	for (int j = 1; j <= n; j++)
            	if (D[i][k] + D[k][j] < D[i][j]){
                	P[i][j] = k;
                    D[i][j] = D[i][k] + D[k][j];
                }
}

$P[i][j] = k;$ ⮕ Shortest Path 상의 마지막 Vertex

Dynamic Programming and Optimization Problems

• Dynamic Programming을 통해 최적해를 구하려면 반드시 Principal of Optimality 조건을 만족해야 한다.
  • Principal of Optimality : Instance의 Optimal Solution은 항상 모든 Sub Instance의 Optimal Solution을 포함한다.
  • Principal of Optimality가 성립하면 Sub Instance의 Optimal Solution을 사용하여 Instance의 Optimal Solution을 표현하는 Recursive Property를 만들 수 있다.
  • Shortest Paths Algorithm은 Principal of Optimality가 성립한다.
• Longest Path Problem은 Principal of Optimality가 성립하지 않는다.