알고리즘 - Dynamic Programming 2

Chained Matrix Multiplication

Matrix Multiplication

• 세 개 이상의 행렬곱을 수행한다면 계산 순서에 따라 곱셈 횟수가 달라짐

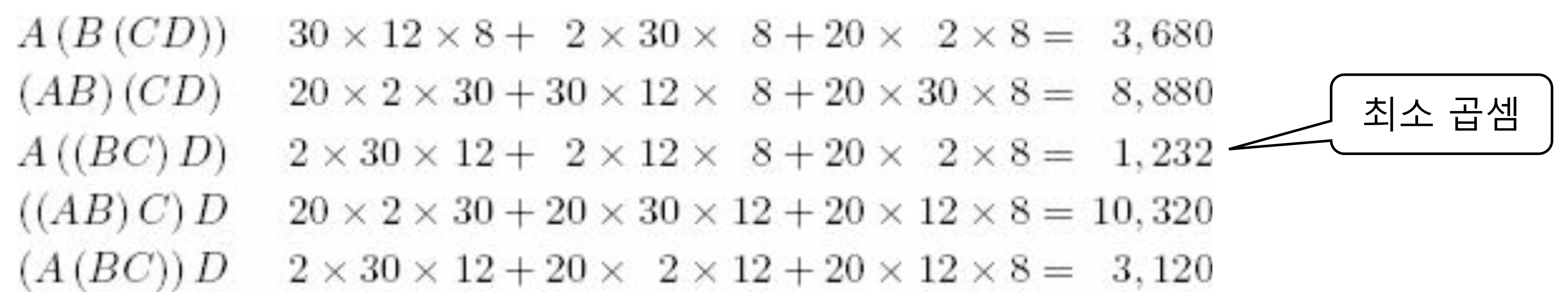
• Goal : 곱셈 횟수가 가장 적은 곱셈 순서 결정

  • Brute-Force algorithm: Exponential Time

  • Principal of Optimality 성립 → Dynamic Programming 가능
    

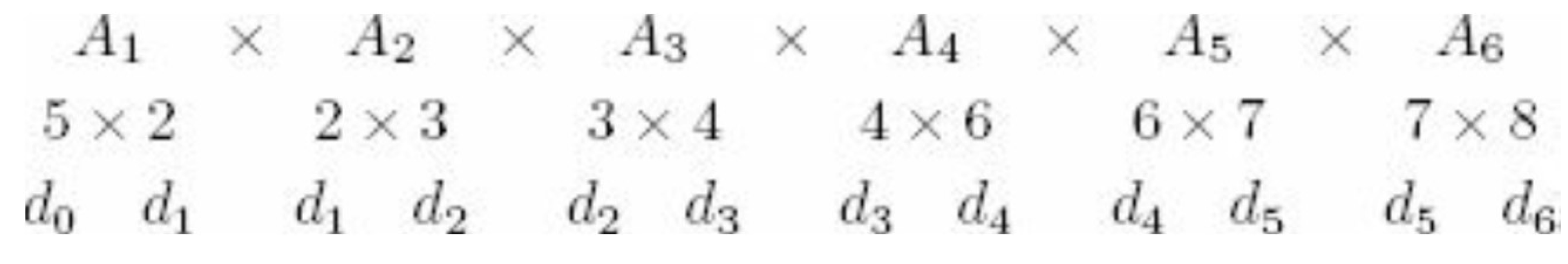
    입력이 위와 같이 주어질 때, 다음 5개 중 하나가 Optimal

  1. $A₁(A₂A₃A₄A₅A₆)$

  2. $(A₁A₂)(A₃A₄A₅A₆)$

  3. $(A₁A₂A₃)(A₄A₅A₆)$

  4. $(A₁A₂A₃A₄)(A₅A₆)$

  5. $(A₁A₂A₃A₄A₅)A₆$

     $A₁((((A₂A₃)A₄)A₅)A₆)$ 이 Optimal이라면 $(A₂A₃)A₄$ 도 Optimal

  • 따라서 다음의 Recursive Property를 만족
    $M[i][j] = minimum(M[i][k] + M[k + 1][j] + dᵢ$₋₁$dₖdⱼ),$ $if$⠀$i$ $< j$
    $M[i][i] = 0$
    ⠀⠀
    최종 솔루션
    $M[1][6] = minimum(M[1][k] + M[k + 1][6] + d$₀$dₖd$₆$)$

    

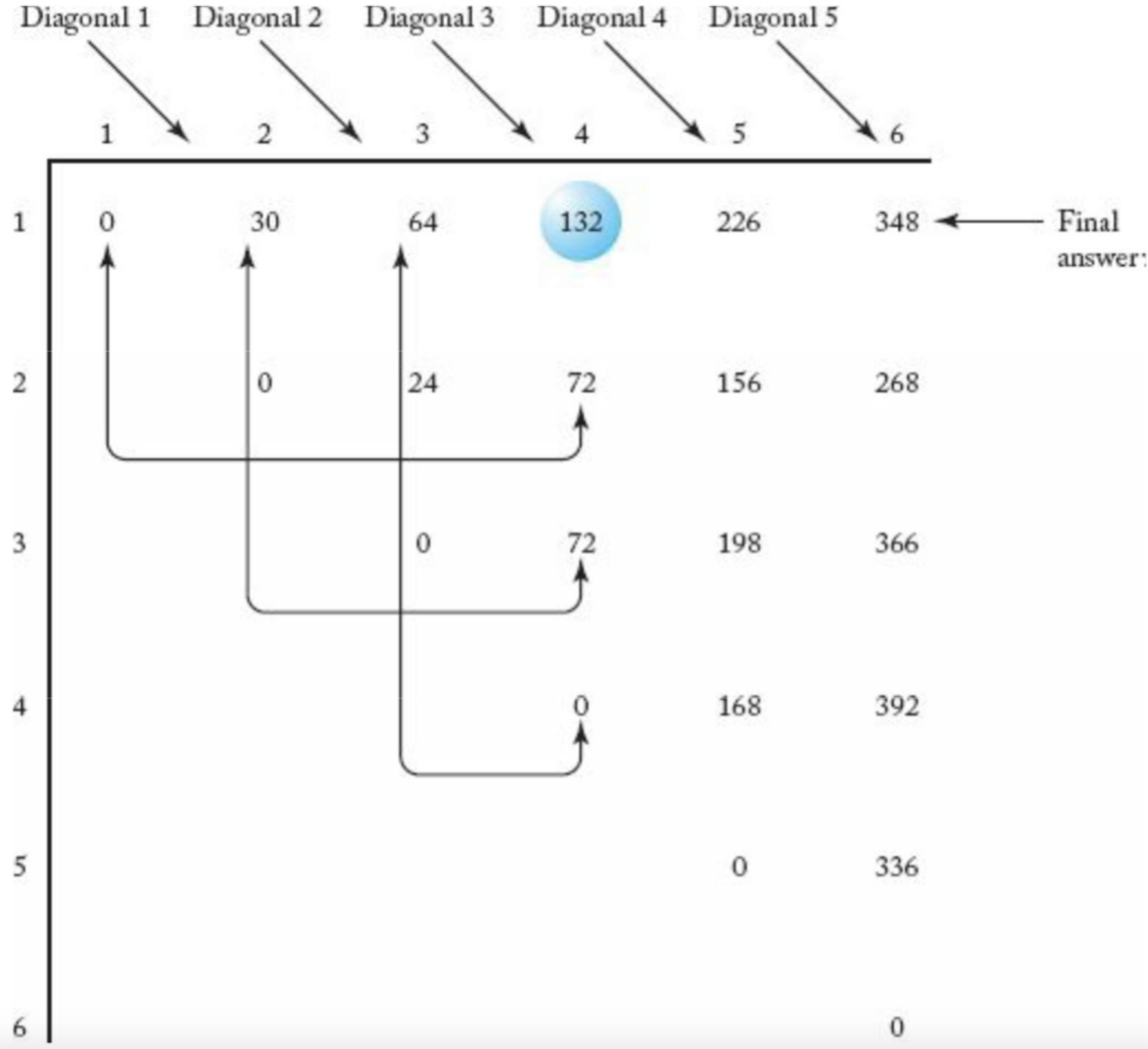
Time Complexity

• Basic Operation: $k$에 대한 연산
• Input Size: $n$
• Complexity: 삼중 Loop로 구성
  • $k$의 실행 횟수: diagonal
  • $i$의 실행 횟수: $n$ - diagonal

Optimal Order

• Optimal Order를 구하기 위해 배열 $P$ 사용

  • $P[i][j]$: $Aᵢ$에서 $Aⱼ$까지의 Matrix 곱셈에서 $M[i][j]$를 최소화 하는 $k$
  • $K[i][j]$ 값을 최소로 만드는 $k$를 발견할 때마다 $P[i][j]$에 $k$를 저장

    

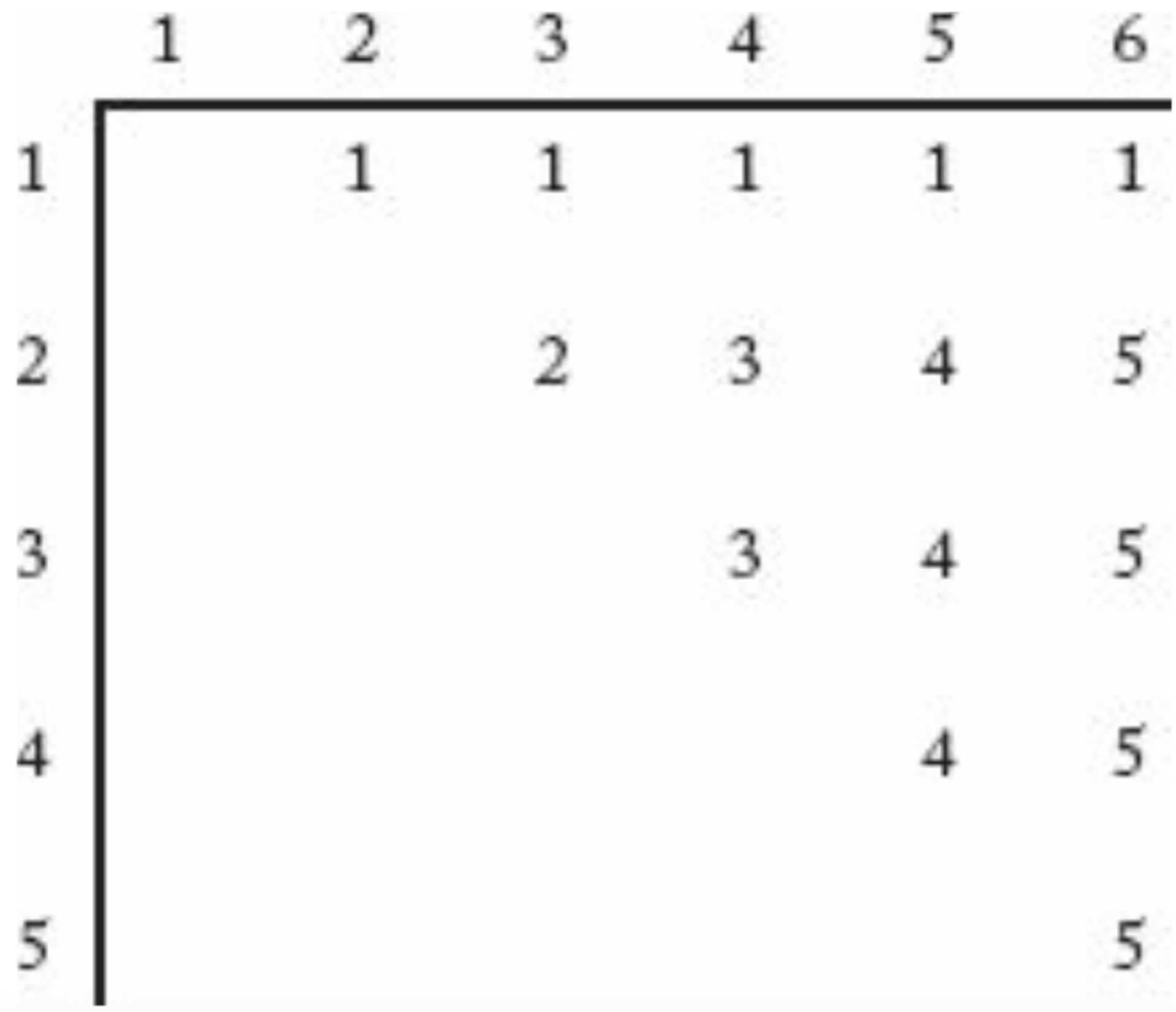
• 1 ~ 6 최소화 → $P = 1$ → $A₁(A₂A₃A₄A₅A₆)$

• 2 ~ 6 최소화 → $P = 5$ → $(A₂A₃A₄A₅)A₆$

• 2 ~ 5 최소화 → $P = 4$ → $(A₂A₃A₄)A₅$

• 2 ~ 4 최소화 → $P = 3$ → $(A₂A₃)A₄$

Code

    for(int diagonal = 1; diagonal < 6; diagonal++)
        for(int i = 0; i < 6 - diagonal; i++){
            j = diagonal + i;
            min = 10000;
            for(int k = i; k < j; k++){
                temp = M[i][k] + M[k + 1][j] + d[i] * d[k + 1] * d[j + 1];
                if(temp < min){
                    min = temp;
                    P[i][j] = k + 1;
                }
            }
            M[i][j] = min;
        }        

Optimal Binary Search Tree

• Definition of Binary Search Tree
  • 각 Node는 Key 값을 가진다.
  • 각 Node의 Left Subtree의 모든 Key 값은 Root Node보다 작거나 같다.
  • 각 Node의 Right Subtree의 모든 Key 값은 Root Node보다 크거나 같다.

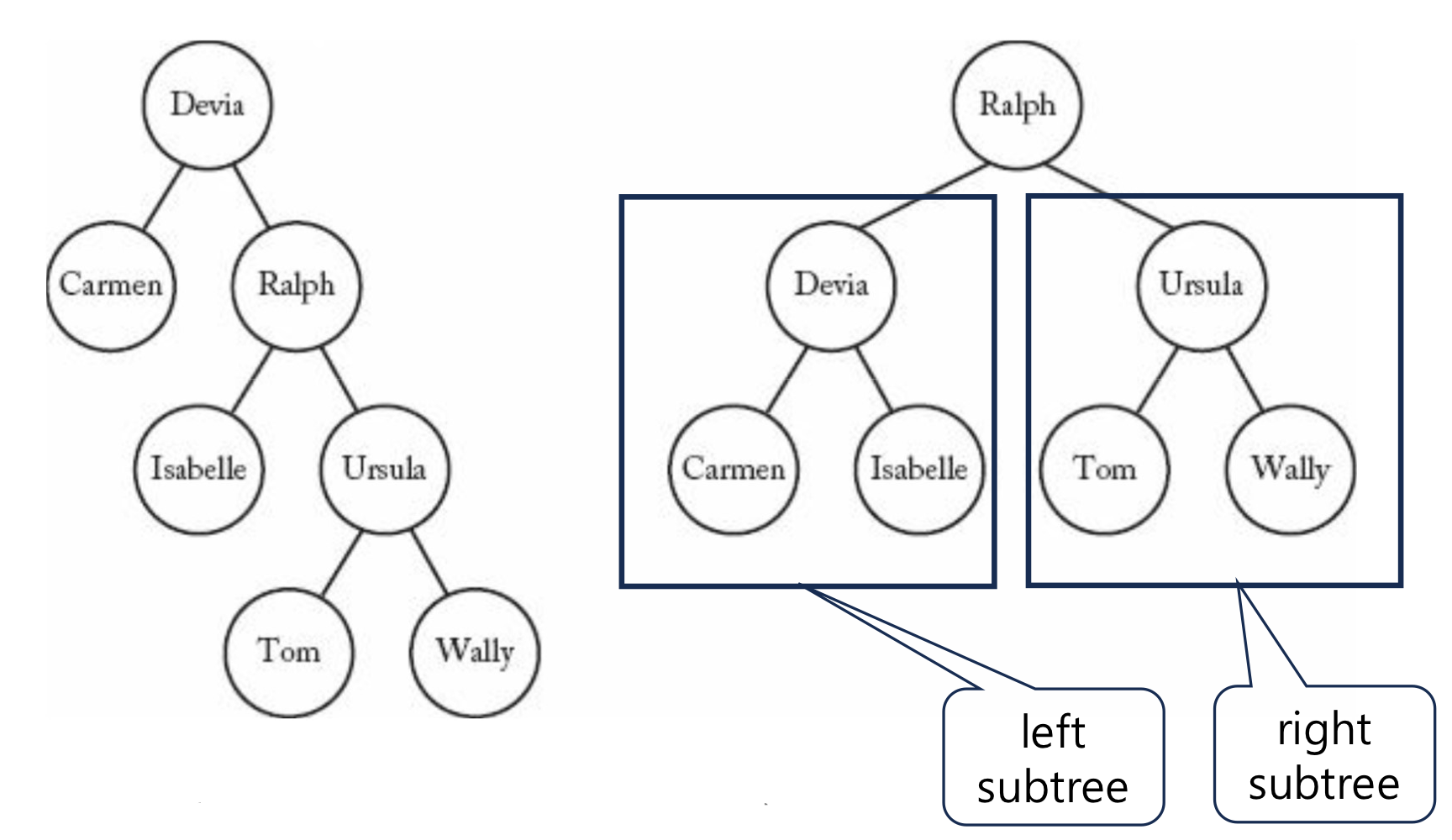
• Definition of Optimal Tree
  • Balanced: 양쪽 Subtree의 Depth 차이가 없을 때
  • Optimal Tree: Tree에서 Key를 검색할 때 가장 적은 시간이 소요되도록 구성된 Tree
    ⠀⠀
• Goal: Key 각각에 대한 확률이 주어질 때 Search Time이 최소가 되는 Binary Search Tree 생성
  ⠀⠀
• 검색 Cost 계산
  • Key를 검색하는데 소요되는 시간: Depth(Key) + 1
  • Keyᵢ를 검색하는데 소요되는 시간을 Cᵢ, 확률을 Pᵢ라고 하면 모든 Key를 검색하는 시간
    → $C$₁$P$₁$+C$₂$P$₂$+C$₃$P$₃ $+$ ··· $+$ $C$ₙ$P$ₙ

Example) $P$₁ = 0.7, $P$₂ = 0.2, $P$₃ = 0.1이고, Key가 정렬된 상태라고 할 때, 각 Search Tree에 대한 검색 Cost는 어떻게 될까?

1. $3 * (0.7) + 2 * (0.2) + 1 * (0.1) = 2.6$
2. $2 * (0.7) + 3 * (0.2) + 1 * (0.1) = 2.1$
3. $2 * (0.7) + 1 * (0.2) + 2 * (0.1) = 1.8$
4. $1 * (0.7) + 3 * (0.2) + 2 * (0.1) = 1.5$
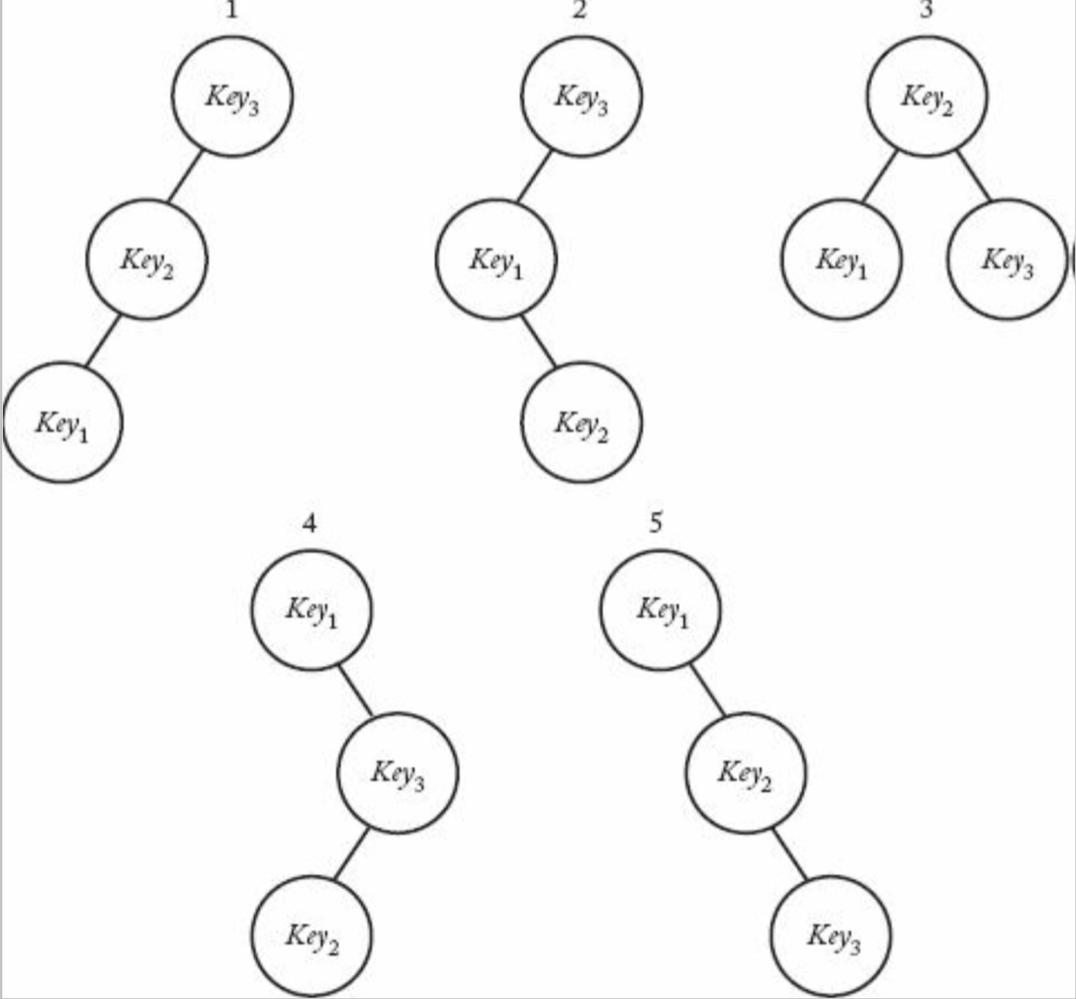
5. $1 * (0.7) + 2 * (0.2) + 3 * (0.1) = 1.4$ → Optimal

• 모든 가능한 Search Tree를 만들어서 최적의 Solution을 구하는 Algorithm의 복잡도는 Exponential
  ⠀⠀
• Optimal Tree의 Left와 Right Sub Tree의 해당 값에 대해 Optimal
  → Principal of Optimality 성립
  ⠀⠀
• Tree K에 대한 평균 검색 시간 계산
  
  따라서 아래와 같은 수식을 생성할 수 있다.
  

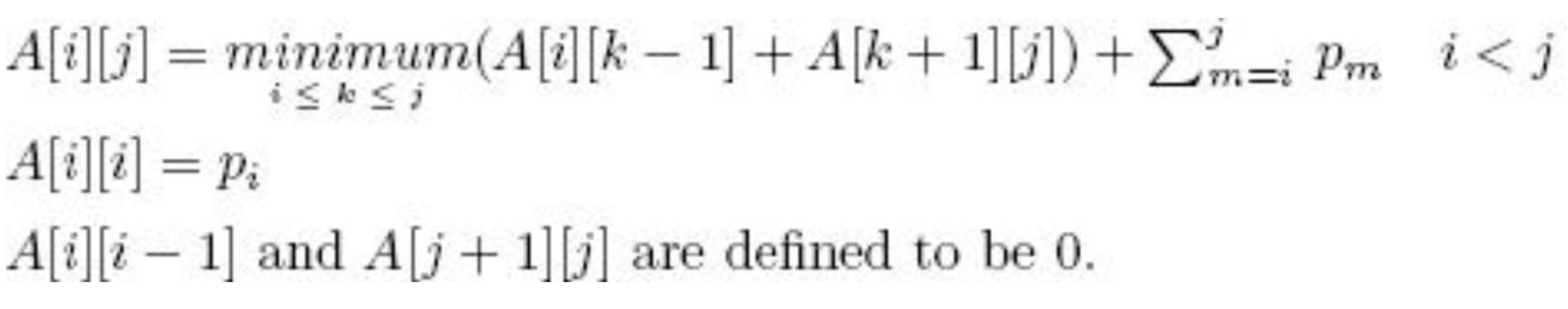
Code

for(diagonal = 0; diagonal < n - 1; diagonal++)
    for(i = 0; i <= n - diagonal; i++) {
        j = i + diagonal;
        min = 100000;
        for(int k = i; i <= j; i++){
            temp = A[i][k - 1] + A[k + 1][j];
            if(temp < min){
                min = temp;
                R[i][j] = k;
            }
            A[i][j] = min + sum of pᵢ ~ pⱼ;
        }
    }
minavg = A[1][n];

• 알고리즘은 Chained Matrix Multiplication과 유사
  • Diagonal 방향으로 계산하여 Optimal Solution으로 확장
  • 배열 $R[i][j]$를 사용하여 해당 Subtree의 Root 노드 획득
  • Time Complexity: $n(n - 1)(n + 4)/6 → Θ(n^3)$
• 모든 Pᵢ가 동일하면 Binary Search가 더 효율적이다.

Traveling Salesperson Problem

• Tour in an directed graph: 임의의 Vertex에서 모든 Vertex를 한 번씩만 경유하여 자신에게 돌아오는 경로

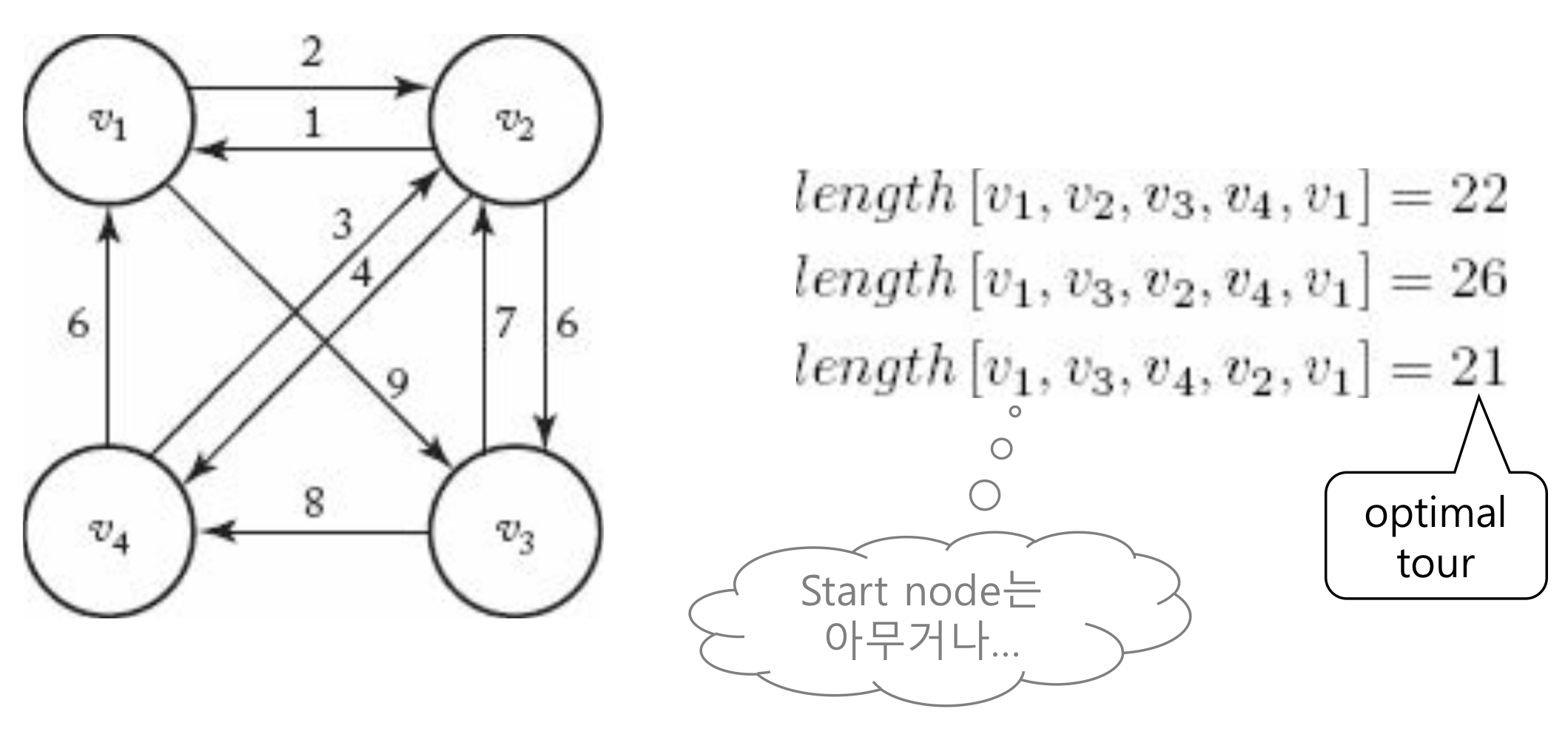
• Complexity - 모든 Vertex가 연결되어 있다는 가정
  $T(n) = (n - 1)(n - 2)$ ··· $1 = (n - 1)!$
  ⠀⠀
• Principal of Optimality 적용 → Dynamic Programming
  • v₁vₖ···v₁ 경로가 Shortest라면 vₖ···v₁도 Shortest
    $D[v$ᵢ$][A] = minimum(W[i][j] + D[vⱼ][A - \{v$ⱼ$\}])$ $if$ $Aⱼ≠∅$
    $D[v$ᵢ$][∅] = W[i][1]$
  • Time Complexity: $T(n) = Θ(n^2$$2^n)$
  • Space Complexity: $M(n) = Θ(n2^n)$
    ⠀⠀
• Dynamic Programming을 사용해도 Exponential Time 소요
  • Vertex의 개수가 적으면 $(n - 1)!$ 알고리즘에 비해 경쟁력이 있다.