Greedy Algorithm

• Greedy Approach
  • 현재 상태에서 최적의 다음 상태를 선택하는 접근 방법
  • 이전 선택을 고려하지 않고 미래의 선택도 고려 X
  • Greedy라는 부정적인 단어를 사용했지만 매우 효율적이고 쉽게 결과를 만들 수 있는 방법
  • Instance를 더 작은 Instance로 분리할 필요 X
  • Selection - Feasibility Check - Solution Check의 단계로 구성
  • Greedy Algorithm이 항상 Optimal Solution을 생성한다는 보장은 없으므로 실행 전 확인 필요

Example

거스름돈 만들기
1. 선택 가능한 동전 중 금액이 가장 큰 동전 선택 - Selection
2. 거스름돈 총액과 비교 - Feasibility Check
⠀⠀ 총액보다 크면 Reject
⠀⠀ 총액보다 작거나 같으면 Accept
3. 거스름돈 총액과 같으면 종료 - Solution Check

Minimum Spanning Tree

Definitions

• Undirected Graph: 방향성이 없는 Edge로 이루어진 Graph
• Path: 한 Vertex에서 다른 Vertex로의 Edge로 연결된 Vertex Sequence
  (Undirected인 경우 u -> v Path가 존재하면 v -> u Path도 존재)
• Connected: Graph 내의 모든 Vertex간 Path가 존재하는 경우
  (직접 연결될 필요 X)
• Simple Cycle: Graph의 한 Vertex에서 자기 자신에게 3개 이상의 Vertex를 포함하는 Path가 존재하는 경우
• Acyclic: Graph 내에 Cycle이 존재하지 않는 경우
• Tree: Acyclic, Connected, Undirected Graph
• Rooted Tree: 하나의 Vertex를 Root로 지정한 Tree
• Spanning Tree: 모든 Vertex를 포함하고 Connected인 Tree
• Minimum Spanning Tree: Weight의 합이 최소인 Spanning Tree

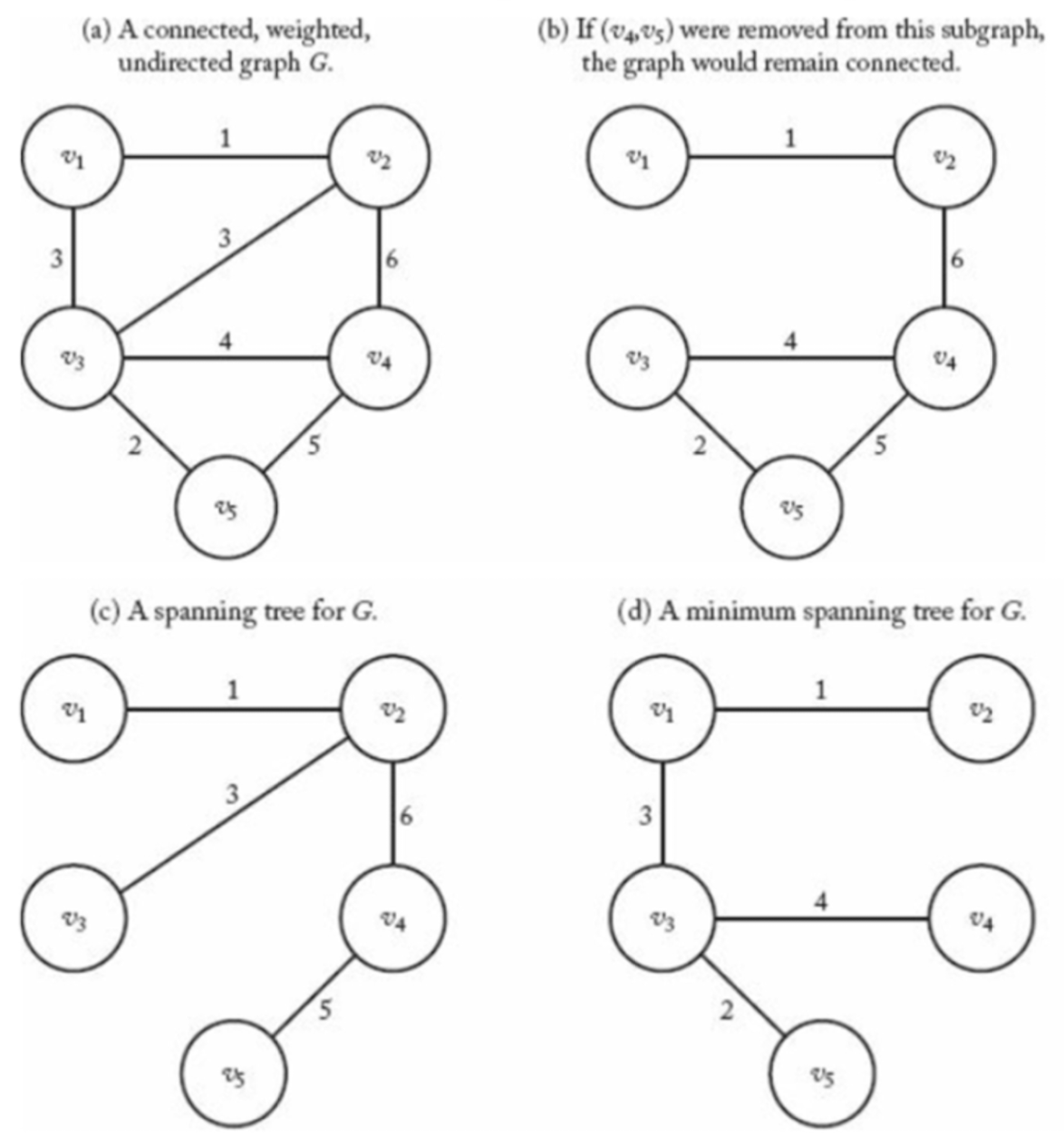
Prim's Algorithm

• 초기값

  • V = {v₁, v₂, ··· , vₙ} - Graph 내 모든 Vertex의 집합
  • Y = {v₁} - Vertex의 부분 집합
  • F = {} - Edge의 부분 집합

• V ↔ Y에 속한 임의의 Vertex 중 Nearest Vertex(Minimum Weight를 가진 Edge)를 Y에, Edge를 F에 추가하여 Y = V가 될 때까지 반복

• Output: Graph에 대한 Minimum Spanning Tree Edge들의 집합 F

  

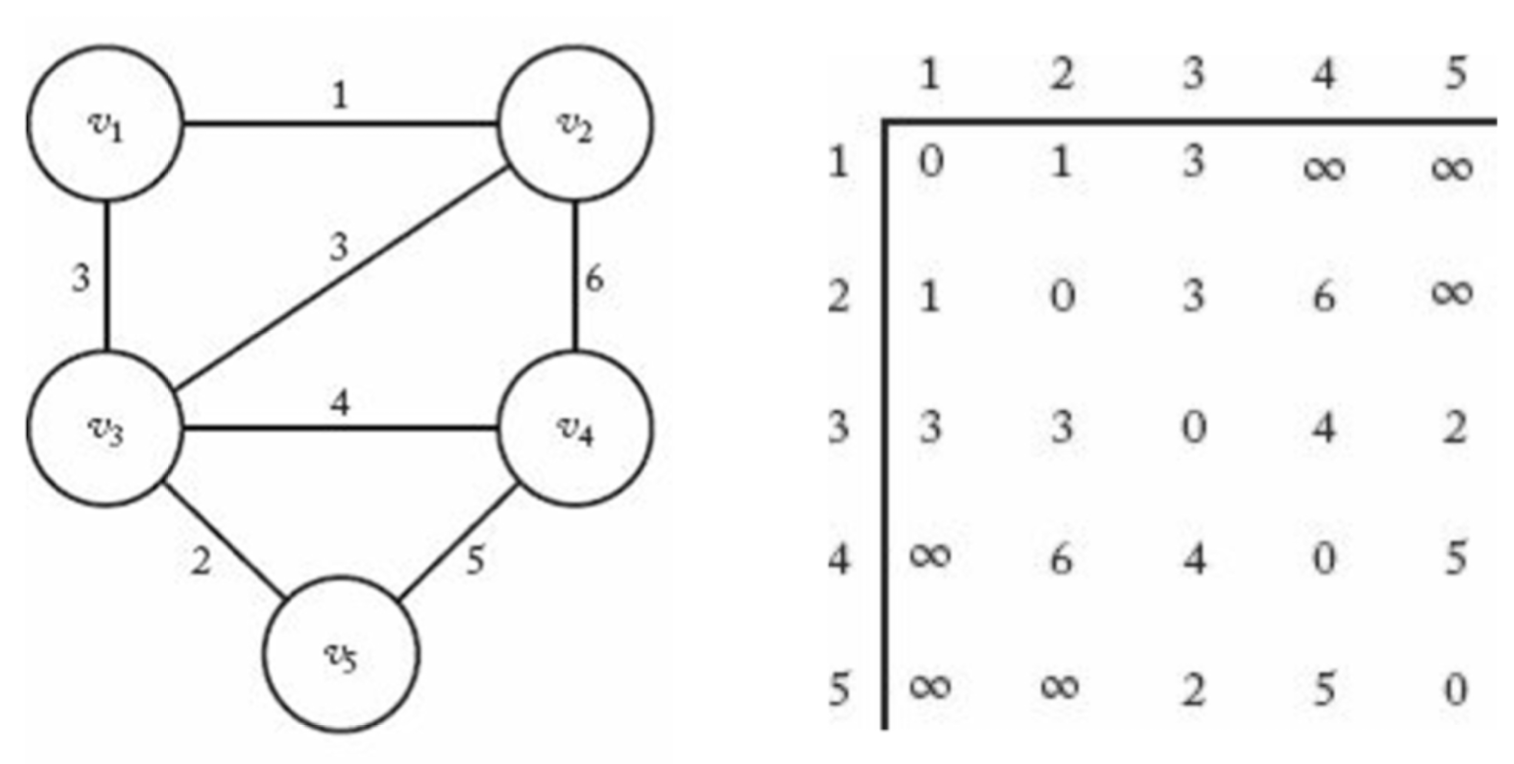
• Edge의 Weight 표현 - Adjacency Matrix
  

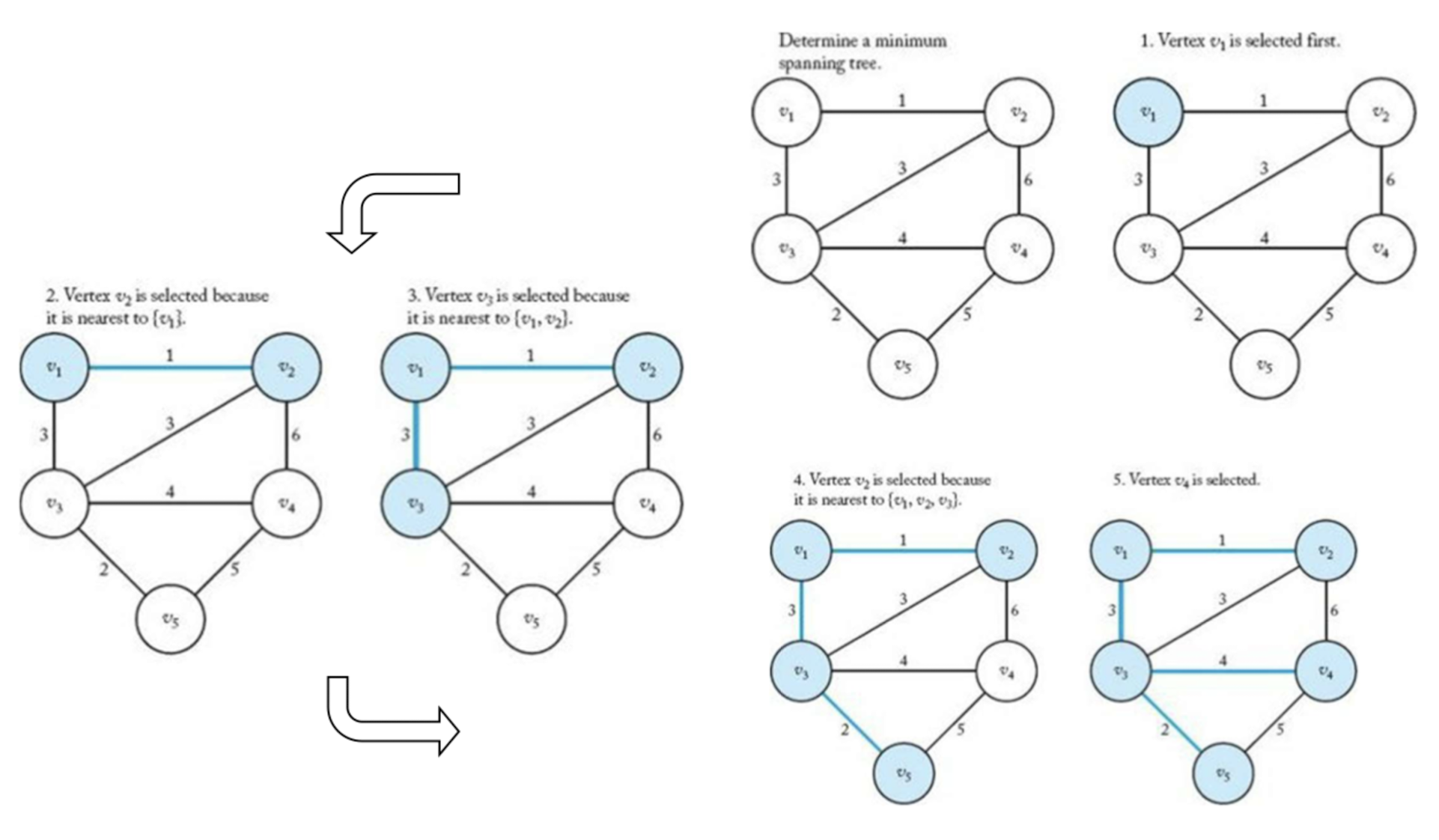
Kruskal's Algorithm

• Minimum Spanning Tree를 구하는 Algorithm
• 동작 방법
  • 각 Vertex를 원소로 하는 V의 Subset을 구성
  • 각 Edge를 Weight 기준으로 오름차순 정렬
  • Edge Weight 순서대로 다음을 반복
    - Edge의 각 Vertex가 서로 다른 Disjoint Subset에 포함되어 있으면 Edge를 F에 추가
    - 두 개의 Disjoint Subset을 병합
    
    ⠀⠀
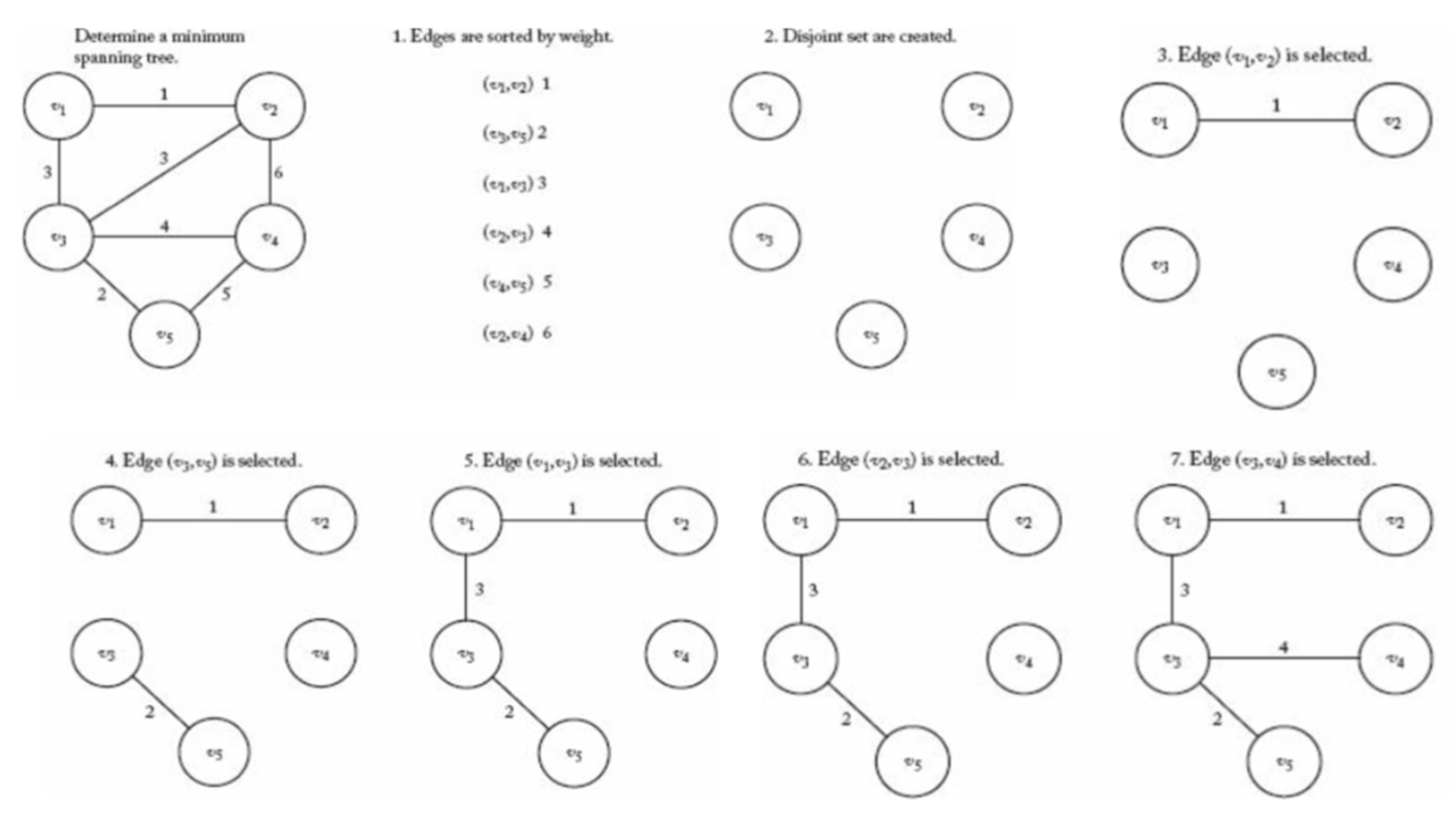
• Complexity: $Θ$($m$$log$ $m$)
  • Worst Case는 모든 Vertex가 Edge로 연결되어 있을 때의 Complexity
  • $n$: Vertex의 개수, $m$: Edge의 개수
    → $m ≥ n - 1$
  • Worst Case일 때 $m = (n - 1) + (n - 2) +$ $···$ $+ 1 = n^2$
  • Edge를 크기 순으로 정렬하는 데 필요한 시간
    $Θ$($m$$log$ $m$) = $Θ$($n^2$$log$ $n^2$) = $Θ$($n^2$$2log$ $n$) = $Θ$($n^2$$log$ $n$)
    ⠀⠀
• 항상 Minimum Spanning Tree의 생성을 보장

Prim VS Kruskal

• Complexity
  • Prim: T($n$) = $Θ$($n^2$)
  • Kruskal: W($m$, $n$) = $Θ$($m$$log$ $m$) → $Θ$($n^2$$log$ $n$)
    ⠀⠀
• Edge의 개수에 따라 성능 차이
  • Edge의 개수와 Vertex의 개수가 큰 차이가 없을 때
    Kruskal = $Θ$($n$$log$ $n$), Prim = $Θ$($n^2$)
  • Edge의 개수가 최대치일 때
    Kruskal = $Θ$($n^2$$log$ $n$), Prim = $Θ$($n^2$)

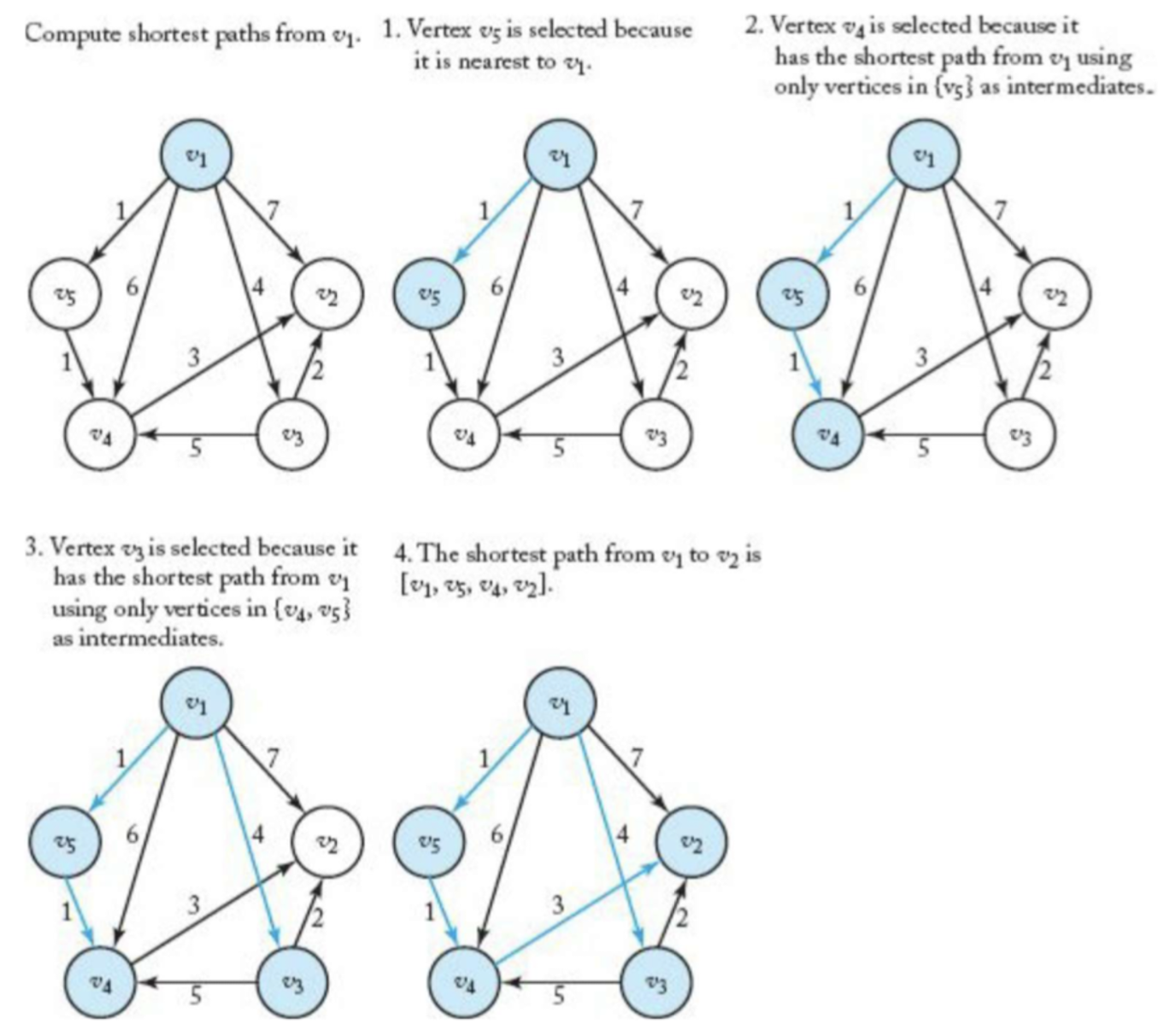
Dijkstra's Algorithm

• Single-Source Shortest Paths Algorithm

  • 하나의 Vertex에서 모든 Vertex로의 Shortest Path를 구하는 Algorithm
  • Greedy Approach($Θ$($n^2$))