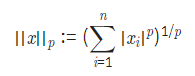학습 목표
- 정칙화(Regularization)의 개념을 이해하고 정규화(Normalization)와 구분합니다.
- L1 regularization과 L2 regularization의 차이를 설명합니다.
- 실습을 통하여 Lp norm, Dropout, Batch Normalization에 대해 학습합니다.
후기
학습 내용
25. Regularization
25.1. Regularization과 Normalization
Regularization : 정칙화
- 오버피팅을 해결하기 위한 방법
- L1, L2 Regularization, Dropout, Batch normalization 등이 있음
- 과적합: train set은 매우 잘 맞히지만, validation/test set은 맞히지 못하는 현상
- train loss는 약간 증가하지만 결과적으로, validation loss나 최종적인 test loss를 감소시키려는 목적
Normalization : 정규화
- 데이터의 형태를 좀 더 의미 있게, 혹은 트레이닝에 적합하게 전처리하는 과정
- 데이터를 z-score로 바꾸거나 minmax scaler를 사용하여 0과 1사이의 값으로 분포를 조정하는 것들이 해당
- 모든 피처의 범위 분포를 동일하게 하여 모델이 풀어야 하는 문제를 좀 더 간단하게 바꾸어 주는 전처리 과정
정리!
Regularization은 오버피팅을 막고자 하는 방법, Normalization은 트레이닝을 할 때에 서로 범위가 다른 데이터들을 같은 범위로 바꿔주는 전처리 과정
Normalization
sklearn.processing의minmax_scale을 이용하여 0~1 범위로 변환
Regularization 방법
sklearn.linear_model의LinearRegression모델을 사용하여 X-Y 관계를 선형으로 모델링sklearn.linear_model에는 L1, L2 Regression인Lasso와Ridge모델도 함께 포함
25.2. L1 Regularization
L1 regularization (Lasso)의 정의
- Lp norm에서 p가 1인 norm을 L1 norm이라고 한다.
수식은 다음과 같다.
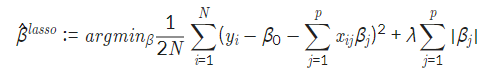
앞의 항은 Linear Regression과 동일하고 뒤에 있는 항이 L1 norm과 일치한다.
- 어떤 컬럼이 결과에 영향을 더 크게 미치는지 확실히 확인할 수 있다.
- error의 차이가 크게 나지 않는다면, 차원 축소와 비슷한 개념으로 변수의 값을 일부만 남겨도 충분히 결과를 예측할 수 있다.
# 참고 지식 (Lp norm)
norm은 벡터나 행렬, 함수 등의 거리를 나타내는 것으로 여기서는 벡터값만 다룸.
Lp norm 의 정의는 아래와 같다.
25.3. L2 Regularization
L2 Regularization(Ridge) 의 정의
- 가중치가 적은 벡터에 해당하는 계수를 0이 아닌 0에 가깝게 보내지만 제곱 텀이 있기 때문에 L1 Regularization보다는 수렴 속도가 빠르다는 장점이 있다.
(제곱 텀에서 결과에 큰 영향을 미치는 값은 더 크게, 결과에 영향이 적은 값들은 더 작게 보내면서 수렴 속도가 빨라지는 것)
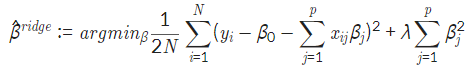
마지막 텀이 제곱 형태라는 점에서 L1 Regularization과 다르다.
25.4. Dropout
- 확률적으로 랜덤하게 몇 가지의 뉴럴만 선택하여 정보를 전달하는 과정
- 오버피팅을 막는 Regularization layer 중 하나
- 확률을 너무 높이면, 제대로 전달되지 않으므로 학습이 잘되지 않고, 확률을 너무 낮추는 경우는 fully connected layer와 같다.
25.5. Batch Normalization
- gradient vanishing, explode 문제를 해결하는 방법
- 중요한 부분은 normalize 부분에서 분모에 이 추가되었다는 점
- normalize 과정에서 gradient가 사라지거나(vanishing), 폭등하는(explode) 것을 막을 수 있음
- 오버피팅이나 학습이 잘되지 않는 것을 막을 수 있게 됨