DataScience 1

정선용·2024년 1월 2일

DataScience

목록 보기

1/7

자료의 이해

기본 용어

통계 용어

모집단(Population) : 통계 분석 방법을 적용할 관심 대상의 전체 집합
모수(Parameters) : 모집단을 분석하여 얻어지는 결과 수치, 통계적 추론에서 분석자의 최종목표이자 모집단(population)의 특성
표본(Sample) : 직접적인 조사 대상이 된 모집단의 일부
통계량(Statistics) : 표본을 분석하여 얻어지는 결과 수치
열 = 변수(Variable) = Feature(특성) = Attribute(속성)
행 = Observation = instance
값 = Label = class = target

Data Type

범주형(Categorical)
: 정성적,질적 자료
빈도 중심 Numerical 분석
빈도 분석 - 글자, 분할표, 파이그래프, 모자이크 plot
- 명목형(Norminal) : 단순히 범주를 표시(ex 성별, 혈액형)
- 순서형(Ordinal) : 범주의 순서가 상대적 비교 가능(ex 비만도, 학점, 선호도)
수치형(Numerical)
: 정량적,양적 자료
범위형, 비율형, 측정오차
평균/분산 Numerical 분석
분포 분석 - 숫자, 히스토그램, Box Plot, 산점도
- 이산형(Discrete) : 셀 수 있는 형태 자료 (ex 멤버 수, 교통사고 건수)
- 연속형(Continuous)
  - 등간형(Interval) : 비교할 수 있도록 단위가 더해진 경우 , +- 연산만 가능 (ex 온도, 점수)
  - 비율형(Ratio) : 0이 없음을 의미하는 경우(절대0점) ,사칙연산 가능 (ex 신장,체중,매출액, 시청률)

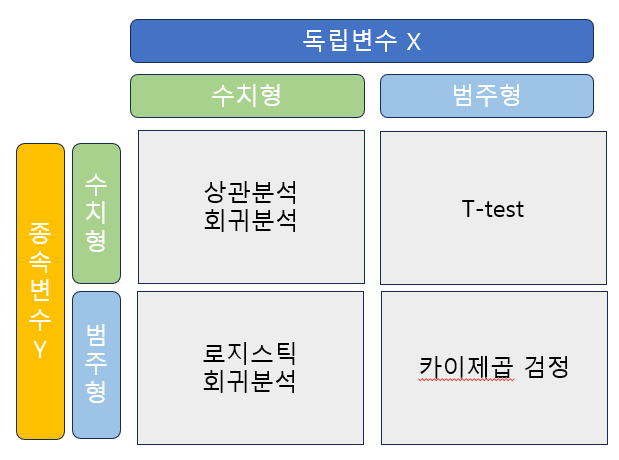
데이터 Type별 통계 분석

시각화

자료의 정리 방법

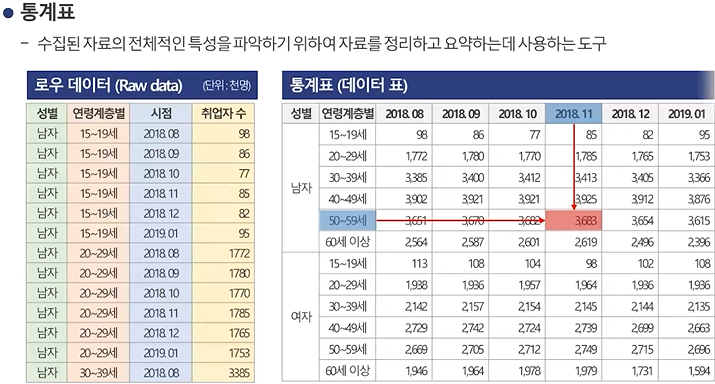
통계표 : 수집된 자료의 전체적인 특성을 파악하기 위해 자료를 정리하고 요약하는데 사용하는 도구
분할표(contingency table), 교차표(tabulation)
: 두 개 이상의 변수를 동시에 고려하여 관측개체의 빈도 정리

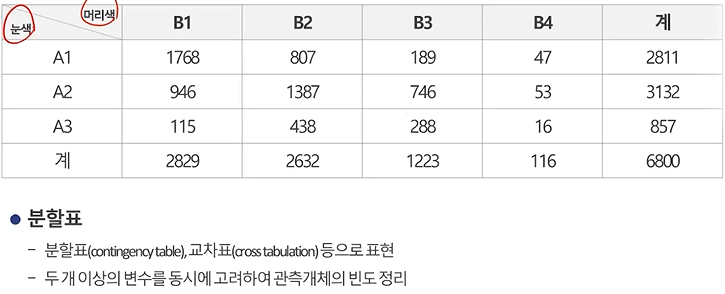
카이제곱검정에서 사용
질적(범주형) 자료
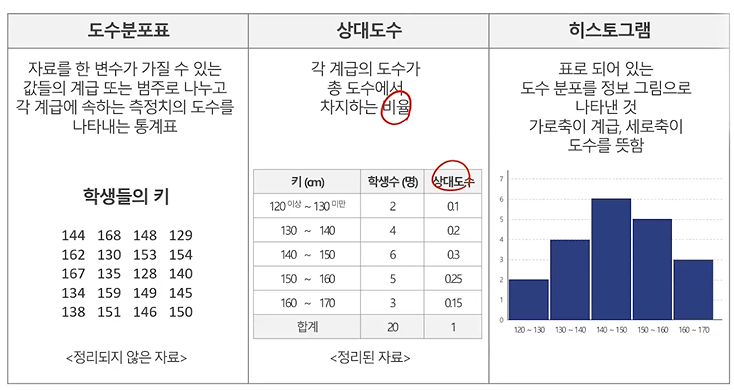
: 도수분포표(도수=자료의 빈도수, 상대도수 = 도수(t)/전체도수(n)), 막대그래프(Bar Chart), 원형그래프(Pie Chart) 등 - - 빈도를 기반으로 함
양적(수치형) 자료
: 도수분포표, 히스토그램(Histogram), 상자그림(Box Plot), 산점도(Scatter plot) 등

차트

일변량 차트(Univariate)

범주형 : 원형(Pie)그래프, 막대(Bar)그래프

수치형 : 히스토그램(Histogram), Box plot

다변량 차트(Bivariate)
- 범주형&수치형 : Box Plot, 막대그래프
- 수치형&수치형 : 산점도(Scatter plot)
- 범주형&범주형 : 모자이크 plot
- 범주형&범주형&수치형 : 누적 세로막대형 차트(Cluster stack column chart)

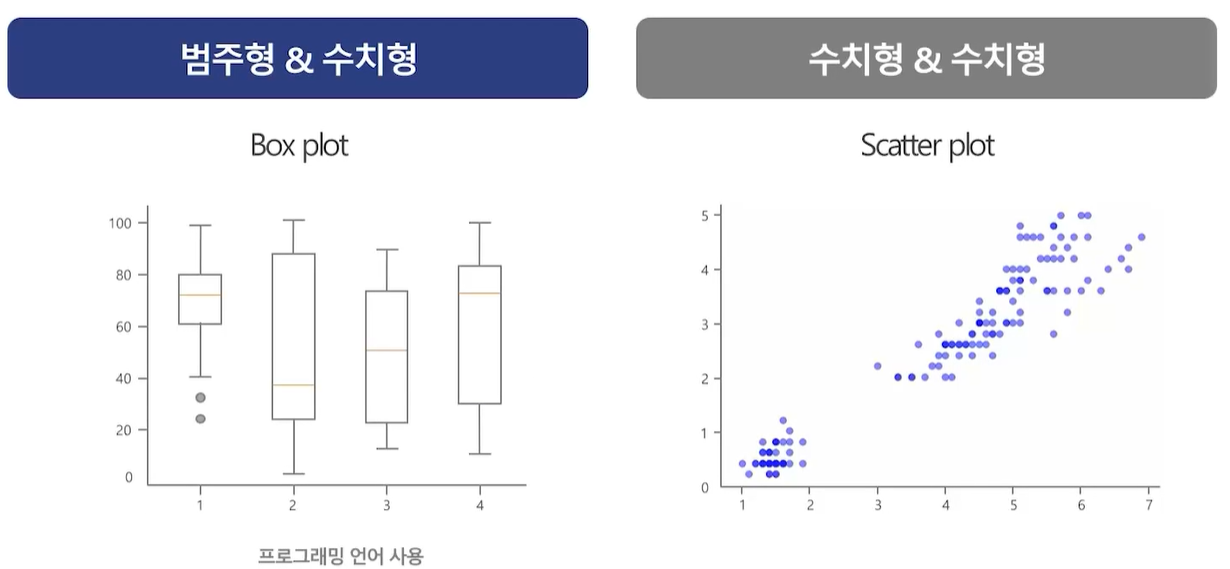
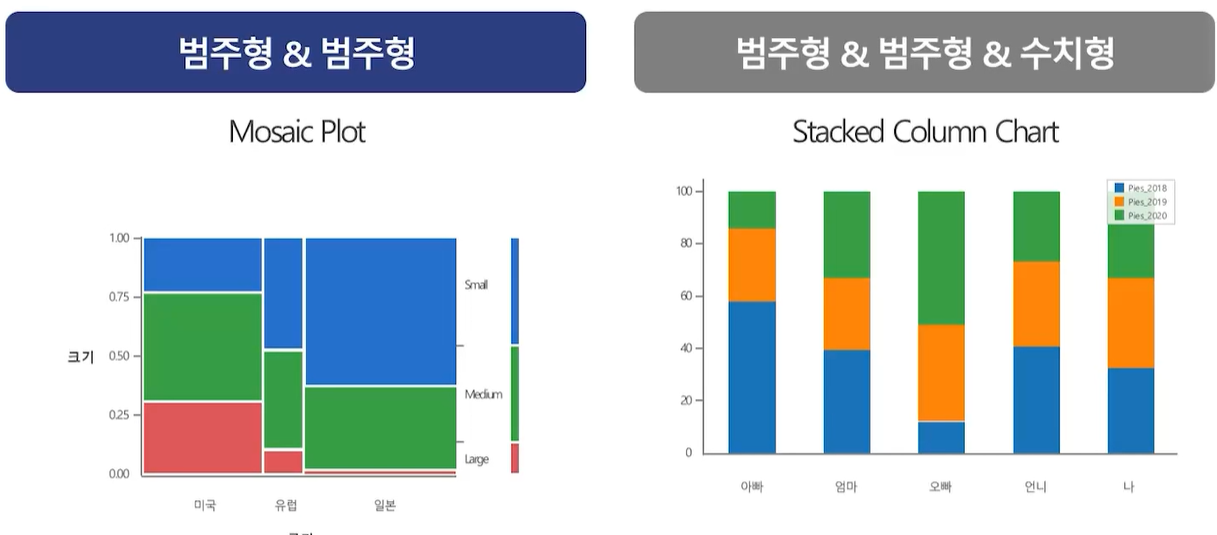
변수가 1개인지, 2개 이상인지, 변수가 범주형인지 수치형인지에 따라 어떤 그래프를 그릴 수 있는지 체크

그래프의 특징

그룹, 이상치 존재 여부를 알 수 있다.

히스토그램(Histogram)	Box Plot	산점도(Scatter plot)
표로 되어있는 도수 분포를 정보 그림으로 나타낸 것	데이터를 사분위수(Quartile)로 쪼개는 것	데이터를 점으로 표현한 것
분포로 그룹, 이상치 존재 여부 확인 가능	box plot수가 그룹의 수이고, 하한,상한을 벗어난 점이 이상치	분포나 점으로 그룹,이상치를 알 수 있음
가로축이 계급,세로축이 도수를 뜻함	모든 데이터가 같은 값을 가지고 있다면 사분위수가 1개로, 선도 1개만 나옴	데이터간 관계성(선형/비선형) 알 수 있음. 인과관계는 알 수 없음)

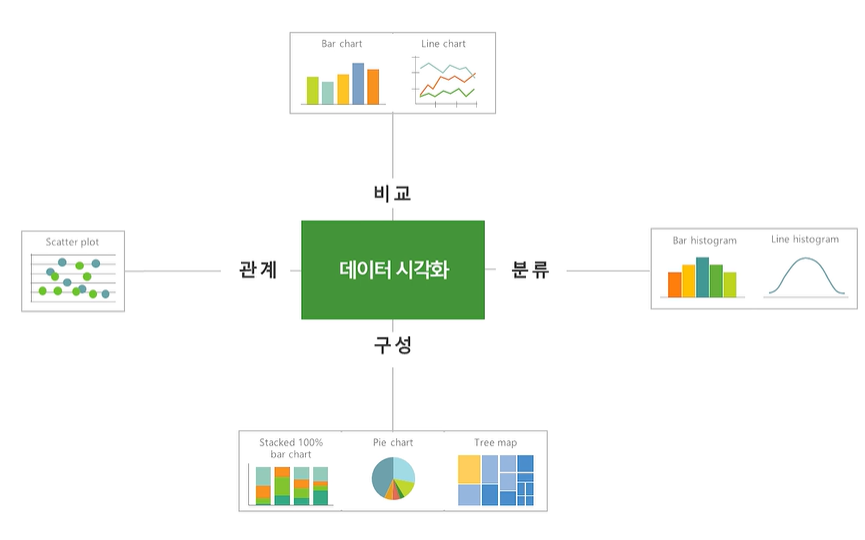
통계분석

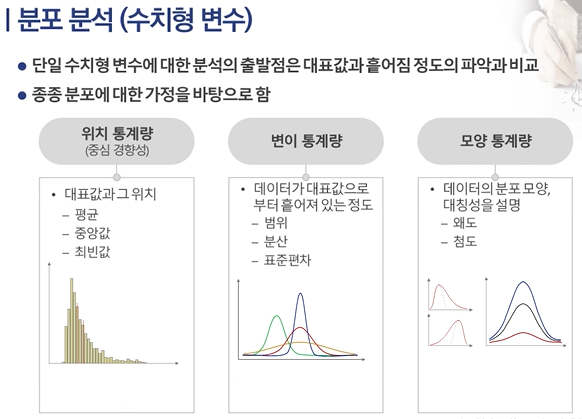
위치 & 변이 & 모양 통계량

통계량
표본을 분석하여 얻어지는 결과 수치, 통계량은 수치형 데이터를 의미 있는 수치로 요약한 것으로, 표본 자료의 전반적 특성을 파악할 수 있음

위치 통계량 : 중심 경향성

: 자료가 어느 위치에 집중되어있는지를 나타내는 척도
(1) 평균(Mean)

분산의 계산, 모수 추정, 가설 검증 등 통계 분석의 대표적인 값.
극단적인 값(이상치)에 민감. (자료수 적고 극단값 여러개인 경우 대푯값 기능 상실)
기대값 E(X) : 평균이 수치형 데이터에 대한 대표값이라면, 기대값은 모집단 데이터에 대한 평균값
기하 평균, 조화 평균, 가중 평균

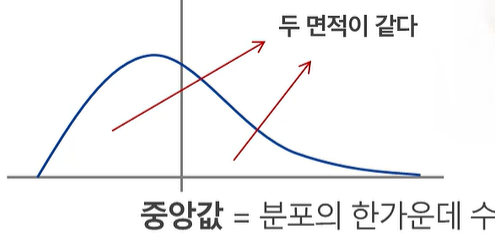
(2) 중앙값(Media) = 중위수

데이터를 순서대로 나열할 때 가운데 값.
짝수일 경우, 가운데 있는 두 개의 수의 평균값
이상치에 민감하지 않으므로 극단적인 이상치가 있는 경우 평균 대신 대푯값으로 사용.

(3) 최빈값(Mode)

데이터 중에서 빈도가 가장 많은 값
자료에 따라 존재하지 않을 수 있고 유일한 값이 아닐 수도 있음.
질적 변수에도 활용 가능(명목,서열 자료에서 대표값)

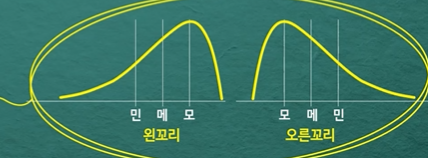
왜도 0이 아닌 경우

오른쪽꼬리가 길면 최빈값-중앙값-평균
왼쪽꼬리가 길면 평균-중앙값-최빈값순.

변이 통계량 (퍼짐 정도)

: 자료가 흩어져있는 정도를 측정, 두 분포에서 자료 산도를 비교하는데 이용

(1) 최소값(minimum)
(2) 최대값(maximum)
(3) 범위(Range) : 최소값,최대값의 차이
(4) 분산(Variance) : 두 분포에서 자료의 흩어짐을 비교하는데 이용

(편차:자료-평균, 모든 편차의 합은 0)
편차^2의 평균을 분산이라고 함.
편차 합은 0이므로 편차의 절대값을 이용(절대편차)하기도 함. 절대편차의 평균은 절대편차평균, 편차제곱의 평균은 분산이라고 함.분산은 제곱한값이므로 원데이터와 단위 달라질 수 있다.
표본분산은 n-1로 나누어야한다.
- 불편추정량(unbias estimator)
  - 모수와 비슷한 값을 만들어주는 추정량.
- 자유도
  - 전체 데이터 중 실질적으로 독립적인 데이터들의 개수.

(5) 표준편차(Standard Deviation): 원래 자료의 단위로 환원되어 같은 단위로 측정된 평균이나 다른 통계량과 쉽게 비교할 수 있음

변이 통계량 특징
- 자료가 흩어질수록 범위,분산,표준편차 증가, 평균 주위로 집중될수록 작아짐, 모두 동일하면 0
- 범위,분산, 표준편차는 양수.

(6) 변동계수(Coefficient of variation, CV) : 상대표준편차, 표준편차를 평균으로 나눈 값. 서로 다른 데이터 간 편차를 비교하는 방법.

모변동계수 : CV = 표준편차/평균
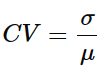
표본변동계수 : CV = 표본의 표준편차 / 표본의 산술평균
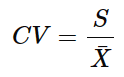
서로 다른 데이터 자체 스케일 차이로 표준 편차 차이가 크게 나올 시, 같은 범위 안으로 표준화 시켜 보고싶을 때 변동계수를 사용.
실질적인 펑균으로부터 데이터 퍼짐 정도를 파악 가능.

모양 통계량(분포의 모양)

: 데이터 분포의 형태와 대칭성을 설명

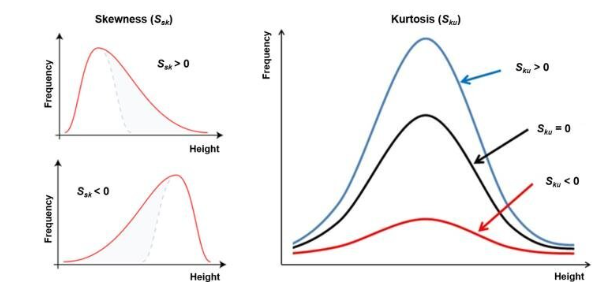
(1) 왜도(skewness) : 분포의 대칭성을 알아보는 측도 - 데이터 분포의 기울어진 정도
(2) 첨도(kurtosis) : 정규분포 대비 봉오리의 높이를 알아보는 측도 - 데이터 분포의 뾰족함의 정도, 큰 편차 또는 이상치가 많을수록 크다.
(3)최소,1사분위수,중앙값,3사분위수,최대값

백분위수(Percentile)
사분위수(Quartile)
사분위수범위(InterQuartile Range,IQR)
상자수염그림(BoxPlot)
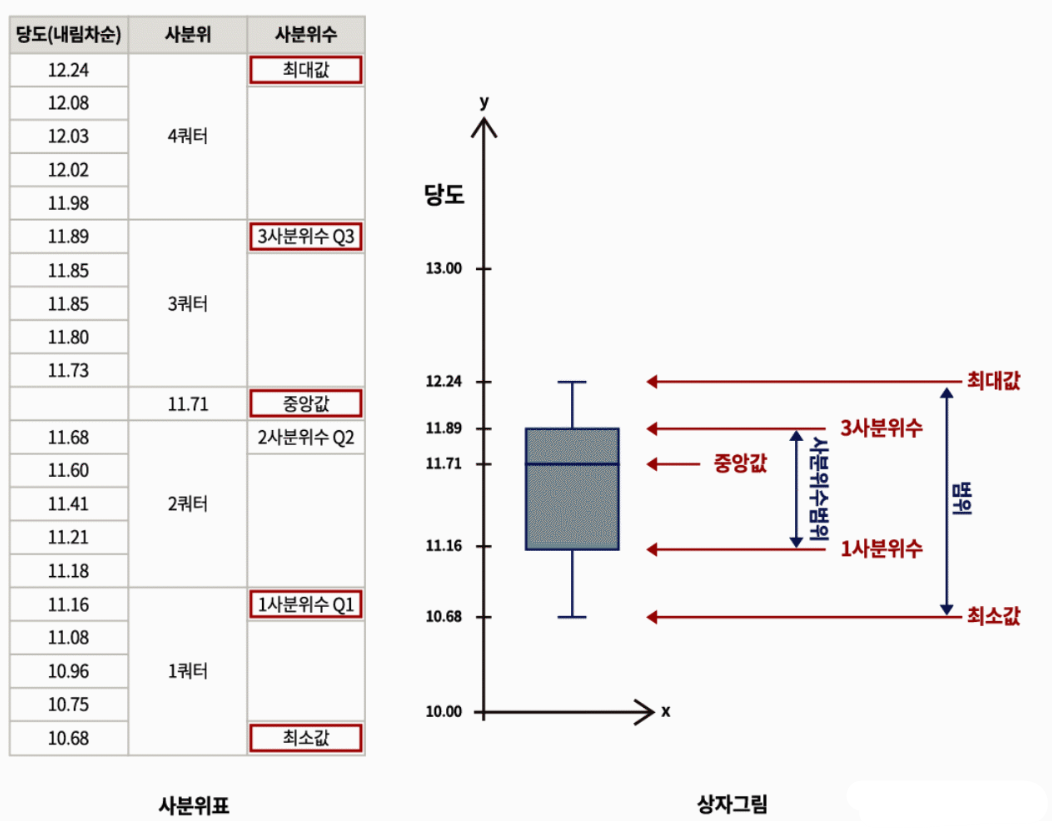
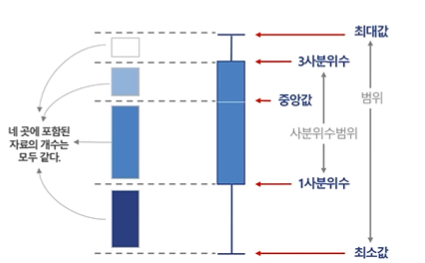
자료분포의 특성을 그래프로 요약,
최소값, 1사분위수, 2사분위수(중앙값),3사분위수,최대값을 표현

특징 정리

위치 통계량
- 계산 쉽고, 각 자료에 대한 유일값 가짐, 통계분석 대표값으로 널리 사용
- 모든 자료로부터 영향-> 극단적 값에 민감,자료 수가 적고 극단값 여러개면 대푯값 기능 상실

확률 & 베이즈 정리

확률

확률
0과 1 사이의 값, 확률의 합은 1, 전체 중 몇 번 일어났나. 전체 사건(표본공간) 중 중 사건이 일어날 가능성
P(A) = n(A)/N
확률실험(E) = 확률시행
다음 3가지를 만족할 경우. 확률실험(시험)이라고 함.
1) 결과는 알 수없음
2) 결과로 나타날 수 있는 가능한 경우들은 알고있음(ex 동전의 앞/뒤)
3) 동일한 실험을 반복할 수 있음
표본공간(S)
확률 실험으로 출현 가능한 모든 결과들의 모임
S:동전던지기 표본공간, H:앞면, T:뒷면 일 때, S=(H,T)
사건
표본공간의 각 원소들의 부분 집합{H},{T}
사건의 연산 : 합사건,곱사건,여사건,배반사건,독립사건

베이즈 정리

조건부 확률
A가 발생한 상황 하에서 B가 발생할 확률
- 확률의 곱셈 법칙
사전확률
사건 B의 원인을 제공하는 확률 P(Ai)
사후확률
사건 B가 발생한 이후의 확률 P(Ai | B)
베이즈 정리(사후확률)
사전 확률과 조건부 확률을 알면 사후확률을 구할 수 있다는 정리.
가능도(likelihood), 사전확률(prior), 관측 데이터(evidence)를 이용해 사후 확률(posterior)를 예측하는 방법

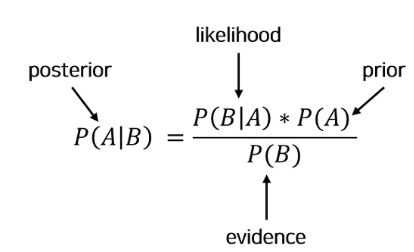
p(A) : A의 사전확률
p(A|B) : A의 사후확률
p(B|A) : 우도(likehood)
p(B) : B의 사전확률
```
	*  P(B|A) = P(A∩B)/P(A)
	*  P(A|B) = P(A∩B)/P(B)
	* P(A∩B) =  P(B|A) * P(A)
	* P(A|B) = P(B|A) * P(A)/P(B)
```
예제
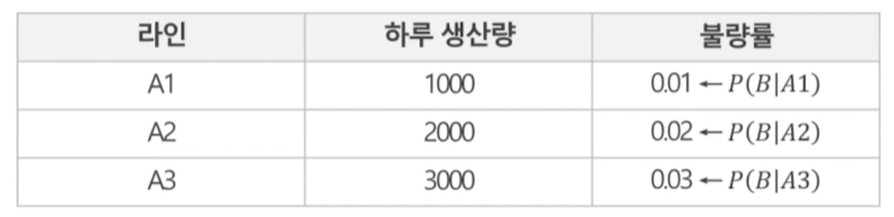
```
생산라인이 3개인 공장이 있다.
각각 하루 생산률과 불량률은 다음과 같다.
이 때 생산된 제품 중 불량을 만났을 때, 불량품이 A1에서 생산되었을 확률은?
```
- 제품이 각 라인에서 생산될 확률(A사전확률)
  : P(A1), P(A2), P(A3)
- 불량률 : A중에 각 라인에서 생산한것으로 판정, 이것이 불량일 확률
  : P(B|A1), P(B|A2), P(B|A3)
- 구하는 값은 6000개 중 불량인 것으로 판정되었을 때, 불량이 A1에서 나왔을 확률 이며,
  - P(B) : 불량일 확률
  - P(A1∩B) : 불량이고, A1에서 생산되었을 확률.
- P(A1|B) = P(A1∩B)/P(B) : 베이즈 정리에 의해 P(A1|B) = P(B|A1)*P(A)/P(B),
  = (0.01 * 1000/6000) / P(B) 이 때
  P(B) = 전체에서 불량일 확률
  = P(A1∩B)+P(A2∩B)+P(A3∩B) = 조건부확률에 의해
  P(A1)(PB|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)
  = (1000/6000)*0.01 + (2000/6000)*0.02 + (3000/6000)*0.03 = 0.023333(14/600)
  이고,
  P(A1|B)= (1/600) * (14/600) = 0.07142857..
```
한번 더 풀이
예제) 불량품을 만났을 떄 A1에서 생산되었을 확률
: P(A1|불량)= P(A1∩불량)/P(불량)
,
P(A1) = 1000/6000
P(A2) = 2000/6000
P(A3) = 3000/6000
,
P(불량|A1) = 10/1000
P(불량|A2) = 40/2000
P(불량|A3) = 90/3000
,
P(불량∩A1)=10/6000
P(불량∩A2)=40/6000
P(불량∩A3)=90/6000
,
//P(불량) = 
//P(A1∩불량)/P(A1|불량) = P(불량)
,
P(불량) = 10+40+90/6000= 140/6000
P(A1|불량) = 10/6000 / (140/6000) = 10/140
=0.07142..
```