DataScience 2

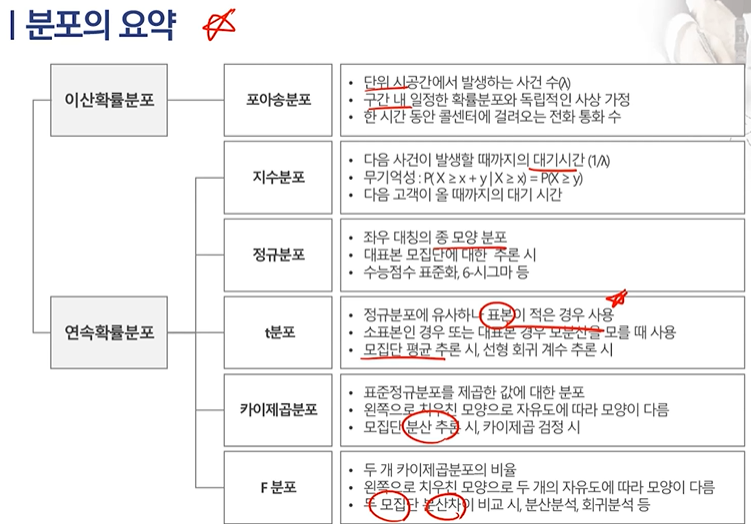
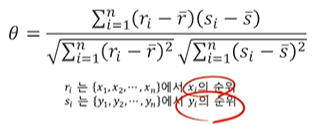주요확률분포

이산, 연속, 균등, 이항, 포아송, 지수

확률변수/확률분포

• 확률변수
  표본공간의 원소를 실수로 대응한 값
  ex) 동전 2개를 던질 때, HH:0,{HT,TH}:1,TT:2 로 mapping .. 범주형이기 때문에 특정 실수로 매핑시켜주는 것임.

• 확률분포
  확률변수와 그 값이 나올 수 있는 확률을 대응시켜 표시하는 것
  ex : 확률변수에 대해 1/4, 2/4, 1/4 로 대응.

  • 확률분포함수 : 확률분포를 함수로 나타낸 것. (x에 대한 함수)

  확률 분포는 이산, 연속, 균등, 이항, 포아송, 지수 종류가 있다.

• 상태공간
  확률 분포에서 확률변수가 취할 수 있는 모든 실수들의 집합(S)

어떤 확률변수가 어떤 확률분포에 대응할 때, 
'확률 분포에 따른다' 라고 함.

확률분포함수

• 확률분포함수
  확률변수 x가 특정 실수 값 x를 취할 확률을 x의 함수로 나타낸 것.
  • 확률질량함수 : 대상 변수가 이산변수
    이산변수, 이산확률분포
    특정한 위치에서 확률을 구할 수 있음.(매핑테이블)
    (probability mass function, PMF)
  • 확률밀도함수 : 대상 변수가 연속변수
    연속변수, 연속확률분포
    구간의 면적이 확률이 됨.(연속함수)
    (probabbility density function, PDF)

이산확률분포의 기대값(평균)과 분산

• 이산확률변수의 평균
  이산확률변수x의 값과 그 값에 대응하는 확률을 곱해 더한 값.
  

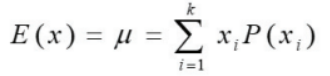
• 이산확률분포의 분산
  
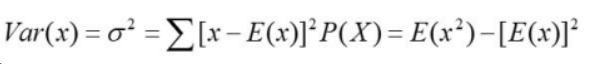
  분산에서 상수곱은 제곱으로 빠진다.

• 이산확률분포의 표준편차

• 기대값의 특성
  

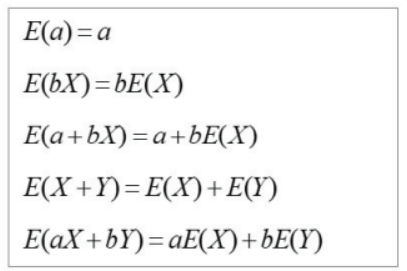
• 분산의 특성
  

균등분포

• 개념 : 확률분포 함수가 정의된 모든 곳에서 값이 일정한 분포
  

  	이산확률변수, 확률질량함수(pmf) = 1/k
  	연속확률변수인경우, 확률밀도함수(pdf) = 1/(b-a) , (a<=x<=b)

이항분포

• 베르누이 실험/시행에 기초, 베르누이 시행을 n번 반복하면 이항실험이 됨.
• 베르누이 시행 : 결과가 두 개인 시행을 독립적으로 반복 시행하는 것
• 조건
  시행을 n번 반복
  각 시행은 성공과 실패라는 상호 배타적인 결과
  n번의 시행은 독립적
  1번 시행할 때 성공확률 p와 실패확률 (1-p)는 시행할 때마다 동일
  * 확률변수 X는 n번 시행 중에서 성공횟수를 의미
  
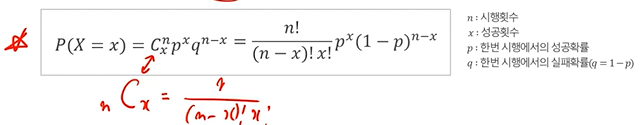
• 특성 : 이항분포의 형태는 모수인 시행횟수 n과 성공확률 p 값에 따라 결정
  • 성공확률 p=0.5에 가까우면 시행횟수 n의 크기에 관계없이 좌우대칭의 종모양(정규)
  • 시행횟수 n이 크면 성공확률 p의 크기에 관계없이 좌우대칭을 이룸
  • 만일 p<0.5이고 b이 작은 경우에 오른쪽 꼬리분포를 나타냄
  • 만일 p>0.5이고 n이 작은 경우에 왼쪽 꼬리분포를 나타냄.
    

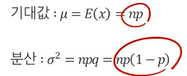
포이송 분포

• 개념 : 일정한 단위시간, 단위거리, 단위면적과 같이 어떤 구간에서 어떤 사건이 랜덤하게 발생하는 경우에 사용할 수 있는 이산형 확률분포
  -> 특정한 단위 안에서 발생하는 횟수의 값을 알아내고 싶을 떄 사용하며, 포아송분포의 람다값이 커질수록 정규분포에 수렴한다.

• 적용 조건

  • 구간마다 발생하는 사건은 서로 독립적
  • 사건의 발생 확률은 구간의 길이에 비례
  • 아주 작은 구간에서 사건이 발생할 확률은 무시할만하다.
    * 구간마다 확률분포는 일정

• 활용 예
  *

  * 1시간동안 은행에 방문하는 고객의 수
  * 1시간동안 콜센터로 걸려오는 전화의 수
  * 책 1페이지당 오탈자가 발생하는 건수
  * 반도체 웨이퍼 25장 당 불량 건수

  포아송에서는 평균=분산=람다(사건발생횟수)
  발생횟수(람다)가 많아질수록 정규형태.
  

지수분포(Exponential)

• 개념 : 시간이 서로 독립일 때, 일정 시간 동안 발생하는 사건의 횟수가 포아송 분포를 따른다면, 다음 사건이 일어날 때까지 대기시간.
• 특징
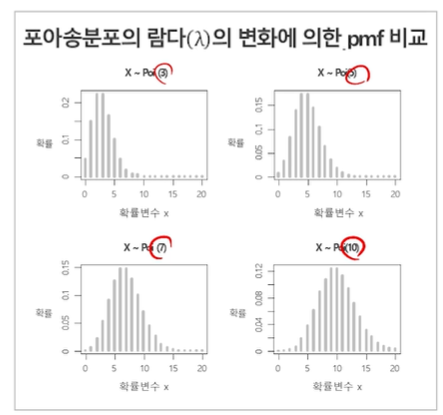
  • 항상 양의 값만 가짐
  • 시간이 지날수록 확률이 작아짐
    • 평균 = 1/람다 , 분산 = 1/(람다^2), (발생횟수에 반비례함)
  • 

분포 종류 추정,검정에 연결되므로 잘 알아둘 것.

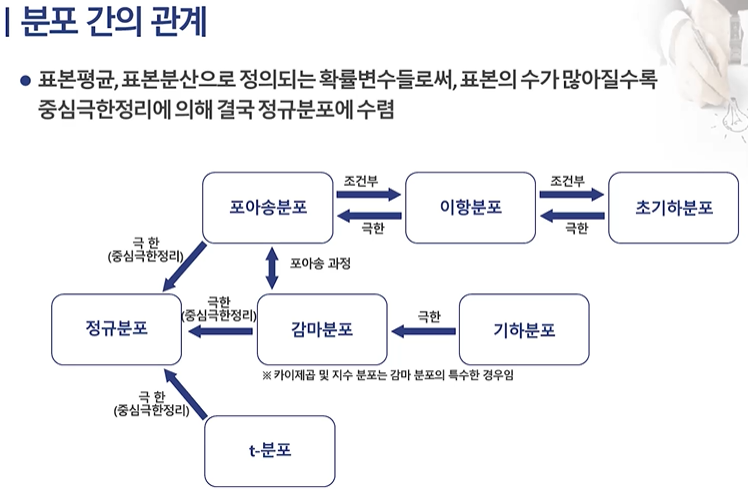
정규, t 카이제곱, f

정규분포

연속확률변수를 기술하는 가장 중요한 확률분포이며,
정규곡선은 종모양을 가진다.

• 중심극한정리
  • 모집단으로부터 각 표본에서 평균들(표본평균) 모집단이 어떤 분포를 따르던 표본평균은 정규분포를 따른다.
• 정규분포는 평균을 중심으로 좌우대칭이며, 평균=중앙값=최빈값.
• 정규분포의 형태와 위치는 평균과 표준편차가 결정한다.
• 정규곡선은 x축에 닿지 않으므로 확률변수 X의 범위는 -무한대 < x < +무한대
• 정규곡선 밑의 면적은 1, 오른쪽으로 또는 왼쪽으로 곡선 밑의 면적은 0.5
• 정규곡선 밑의 두 점 사이 면적은 정규확률변수가 이들 두 점 사이를 취할 확률.
• 평균 주위로 +- 표준편차, +-2표준편차, +-3표준편차 안에 약 68%, 95%, 99% 의 데이터 있음.
  
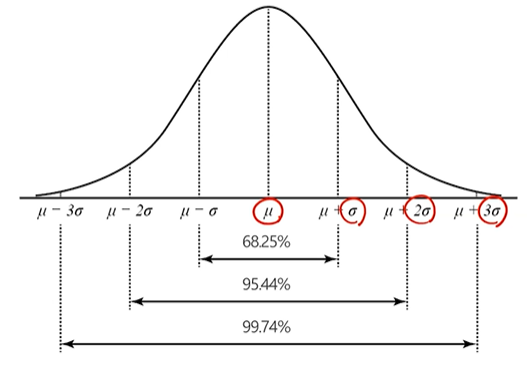
  중요) 2sigma범위-> 95% (신뢰구간 연관)

표준정규분포

• 정규분포를 표준화.
  
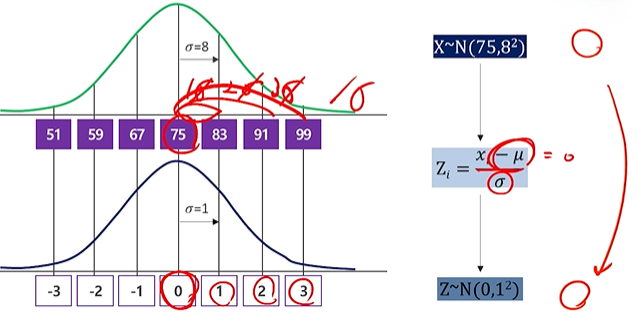
  (평균 뺴주고 표준편차(시그마)로 나눠줘 평균은 0, 시그마 표준편차구간은 1,2,3로 )
• 확률변수 Z가 평균 = 0, 분산 = 1, 분산 = 1인 정규분포
• 1.96~1.96 안에는 95% (+- 2표준편차) 데이터가 있음.
• Z분포. Z~N(0.1)로 표현.
• 서로 다른 평균과 분산을 가진 분포 사이의 비교가 가능
• 확률변수 계산
  (1) 주어진 x값을 평균과 표준편차를 이용해 z값으로 변환
  
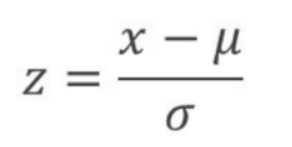
  (2) 표준정규분포표 혹은 주어진 z값 정보를 이용하여 확률 확인

t분포( Student's t-Distribution)

• 모집단의 평균을 추론할 때 사용.(표본 -> 모집단)

• 정규분포와 유사하게 좌우 대칭의 종모양, 중심은 0

• 자유도에 따라 형태가 달라짐
  표본의 수 크면-> 표준정규분포와 거의 같아짐
  표본의 수 작으면-> 양쪽 꼬리가 더 두터워짐(덜중앙집중)
  

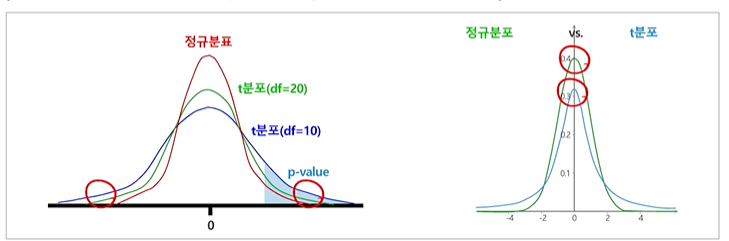
• 표본의 수가 적을 경우 평균 검정을 위하여 고안된 분포

• 확률변수계산
  
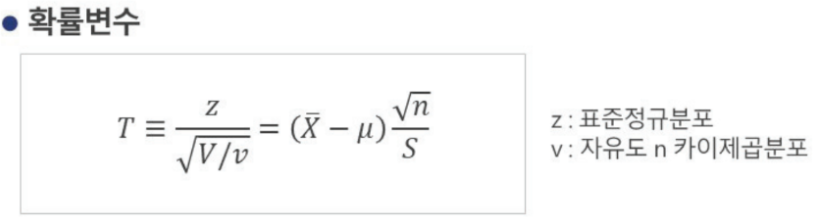
  s/n^(1/2) : 표준오차

카이제곱 분포

• 모집단의 분산을 추론할 때 사용
• 표준정규분포를 제곱한 값에 대한 분포(k개의 정규분포의 제곱합)
• 항상 양수이며 자유도가 커질수록 정규분포에 가까워짐(k개, 정규분포 개수가 늘어날수록 자유도가 커진다)-> k커질수록 정규분포
• 오른쪽꼬리 분포로 자유도가 커질수록 정규분포에 가까워짐

F분포

• F-검정, 분산분석, 회귀분석에서 이용.
• 두 개의 카이제곱분포의 비율
• 두 분산 간의 동질성 여부를 검정하거나 두 개 이상의 평균치간 차이 유무를 검정
• 항상 양수, 자유도가 커질수록 정규분포에 가까워짐
• 왼쪽으로 치우친 모양으로 두 개의 자유도에 따라 모양이 다름

추론통계, 상관분석

추정

추정

• 통계적 추론 : Statistical Inference, 모집단에 대한 미지의 것을 알아내려고 통계학을 이용하여 추측하는 과정으로, 추정과 가설검정으로 나눌 수 있음.
• 추정 : 표본을 통하여 모집단의 특성이 어떠한가에 대해 추측하는 과정
  추정량 : 모수를 추정하는데 사용되는 표본 통계량(가설검정에서는 검정통계량으로 부름)
  추정치 : 추정량을 평가하여 얻게 되는 특정한 수치.
• 점추정(Point Estimation)
  모집단의 특성을 단일한 값으로 추정하는 방법(고정된 값)
  모르는 모수를 가장 잘 대표할 수 있는 표본을 추출하고 필요한 계산을 하여 얻는 하나의 수치(표본평균과 표본분산 등이 대표적인 점추정량)
  표본이 모집단의 특성을 잘 표현하지 못한 경우에는 통계량과 모수 간의 오차가 클 수 있음.
  추정이 잘 되려면 모집단을 대표하는 표본 추출이 잘 이루어져야 한다.
• 구간추정(Interval Estimation)
  모수의 참값이 포함되리라고 기대하는 추정치를 일정한 범위로 나타내는 것
  모수가 있을 것으로 예상되는 구간과 그 구간에 실제 모수가 있을 예상 확률을 구함.
  구간 설정 : 구간이 좁으면 모수를 좀 더 정확하게 추정하는 것
  신뢰도 설정 : 설정된 구간에 실제 모수가 존재할 확
  * 구간의 상한/하한 내에 표본평균이 있음.

중심극한정리

• 대수의 법칙 (큰 수의 법칙)
  장기적으로 어떤 사건이 일어날 확률과 그 사건이 일어나는 상대적 빈도 사이 차이는 궁극적으로 0에 접근
  표본 수가 많을수록 실사건의 확률이 통계적 예측에서 오차가 줄어감(통계량의 오차는 0에 접근)
• 중심극한정리 : 표본이 커지면 정규분포에 가까워
  * 동일한 확률분포를 가진 독립확률 변수
  n개의 평균
  의 분포는 n이 적당히 크다면 정규분포에 가까워짐
  • example) 주사위던지기
    

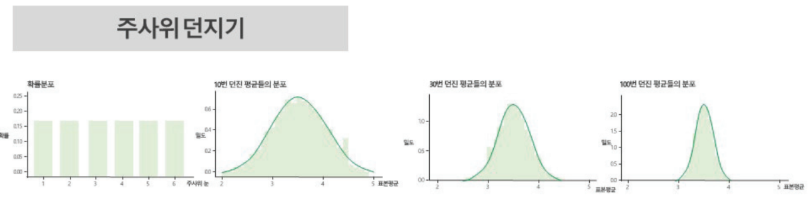
    ※ 모집단이 어떤 분포를 가지던 간에(분포 모양 상관 없이) 표본의 크기가 충분히 크다면 표본평균들의 분포가 모집단의 모수를 기반으로 한 정규분포를 이룬다는 점을 이용하여, 특정 사건(내가 수집한 표본의 평균)이 일어날 확률값을 계산할 수 있게 된다. 즉, 중심극한정리를 통해 표본평균들이 이루는 표본 분포와 모집단 간의 관계를 증명함으로써 수집한 표본의 통계량을 이용해 모집단의 모수를 추정할 수 있는 수학(확률)적 근거를 마련해 주는 것.

신뢰구간(Confidnece Interval)

• 모두가 포함될 것이라고 주장하는 범위
  P(하한<점추정치<상한) = 0.95

• 신뢰구간의 계산 (중요)
  

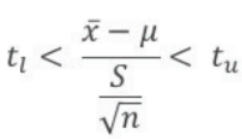
  • 오차율
    

  • z분포나 t분포의 계산식 동일.(계산 시 t value만 바꿔주면 됨)

  • t자리에 z / t가 오냐에 따라(=z분포인지, t분포인) 신뢰구간 하한/상한값이 달라짐

  • 신뢰구간이 좁을수록 정확도가 높다.
    
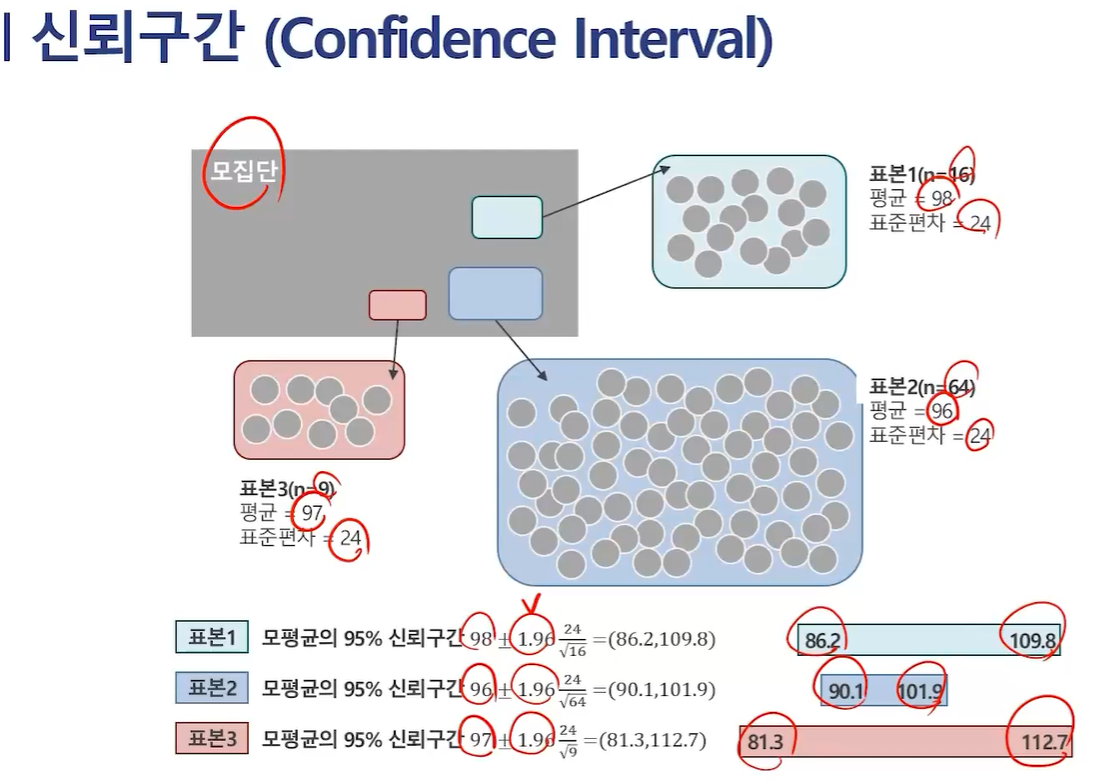
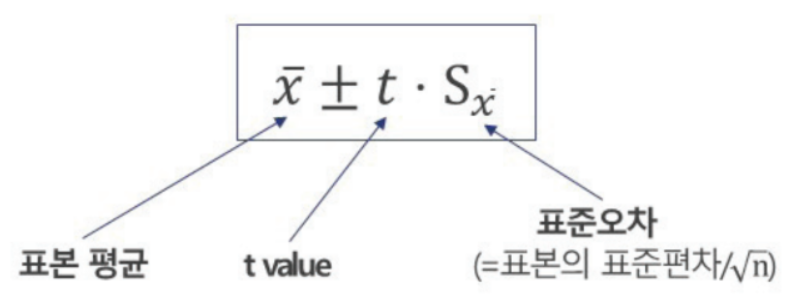
    포본 1에 대한 95% 신뢰구간 = 표본평균 += t 표준오차
    = 98 += 1.96 (표준편차 / n^(1/2)) = 98+= 1.96 * (24/4) = 98+=11.76
    -> 86.24 ~ 109.76

신뢰수준

• 모수의 참값이 두 신뢰 한계 안에 포함될 것이라고 주장할 때 사용하는 확률.
• 대표적으로 90%, 95%(Z분포), 99% 신뢰 수준을 사용
• 모수 μ에 대한 95% 신뢰 구간이란 n번 반복추출하여 산정하는 많은 신뢰구간 중 평균적으로 95%는 모수 μ를 포함하고 있을 것이라는 의미.
• 추정 시 유의점
  모분산 알때는 Z분포 사용
  모분산 모르지만 n값이 30 이상일 떄도 Z분포 사용
  모집단이 정규분포이며 모분산 모르고 n값도 30 미만일 때 t분포 사용.
  계산 문제가 나오면 상한/하한값은 주어지긴한데. 95% 신뢰수준이 자주 사용되니 z분포이면서 자유도 = 무한, 신뢰수준95%일 때 상한/하한값 -+1.96은 기억해둘 것

표준 오차

• 통계학적 의미 '오차'는 한정된 데이터를 통해 얻어진 평균 또는 비율이 'True'로 부터 어떤 확률과 정도로 벗어나 있는지를 나타내는 것

• '표준오차'는 표본 평균의 퍼짐 정도(표본 평균의 표준편차)
  

  ![](https://velog.velcdn.com/images/jeongsunyong/post/f480b5a7-31bb-468a-b972-44782d8a0200/image.png)

  
  

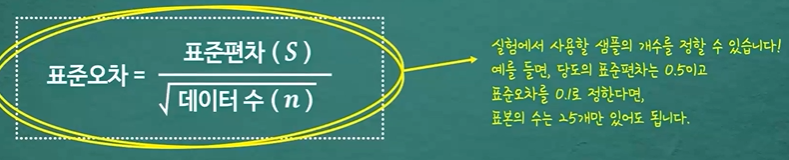
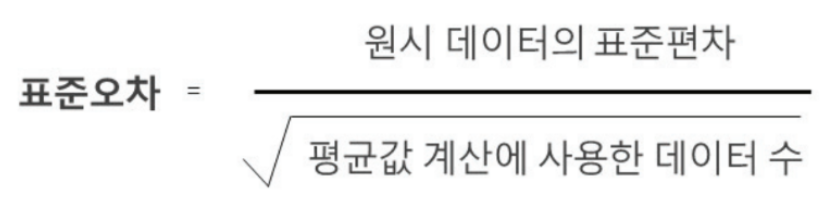
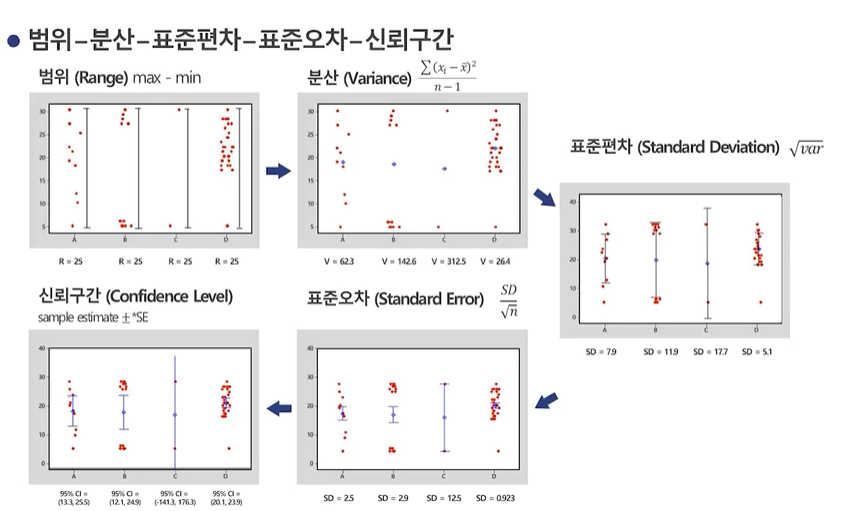
  신뢰구간은 표준오차보다 작을수도, 클수도 있다.

상관분석

상관분석

• 상관분석이란?
  연속형 두 변수 간 선형(직선)적 관계 정도를 검정하는 통계 분석 방법
  ex 교육과 임금, 통화증가율과 물가상승률 등..
• 가장 쉽고 빠르게 선형성을 확인할 수 있는 방법으로 산점도 사용
• 산점도
  * 두 개의 숫자형 데이터를 직교 좌표계에 표시하여 두 변수 간 관계를 나타내는 방법
• 산점도를 통해 확인해야할 사항
  두 변수 간 선형관계(직선)가 존재하는가?
  두 변수 간 함수관계(직/곡선) 가 존재하는가?
  자료에 이상점(Outlier)가 존재하는가?
  몇 개의 그룹으로 나누어 구분할 수 있는

상관계수

• 두 변수 사이의 상관관계의 정도를 나타내는 수치(선형성이 얼마나 강한지)

• 1에서 1 사이 범위를 가지며, 절대값이 1에 가까울수록 강한 상관관계.
  

• 피어슨 상관계수(Pearson correlation)
  두 변수 간 선형 관계의 방향과 강도가 어느 정도인지 측정
  (-1 <= r <= 1) , 양 끝에 가까울수록 강한 상관관계
  두 변수에 정규성 가정. **
  귀무가설 : 두 변수 간 상관관계가 없다.

  • 상관계수 r =

• 스피어만 상관계수(Spearman correlation)
  순위(서열척도) 자료간 상관관계를 파악 가능.
  원 변수값 대신에 변수값들의 순위 * 를 이용하여 피어슨 상관계수 공식을 활용.
  (-1 <= r <= 1) 양:비례, 음:반비례
  * 비모수적 방법(정규분포를 벗어날 떄 사용)

  • 

• 켄달 상관계수 (Kendall correlation)
  순위(서열척도) 자료 간 상관관계를 파악 가능.
  두 변수를 크기 순으로 계산한 후, 각 변수별 순위에 상호 일관성이 있는지를 Condordant와 Discordant의 갯수 이용하여 계산.
  *

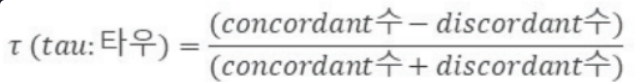
  		* ex) 대회 참가자중 심사위원1이 준 등수는 A가 우수, 심사위원2가 준 등수는 B가 우수하였다면 이는 Discordant.
  	* 비모수적 방법(정규분포를 벗어날 때 사용)

• 상관계수 비교
  

상관계수에 대한 이해

• 상관관계가 있다고 해서 인과관계가 있는 것은 아님
• 인과관계가 없기 때문에 상관계수로 기울기를 알 수 없다.
• 상관계수 절대값이 0에 가깝다고 해서 두 변수 관계가 없는 것 아닐 수 있고 상관계수 절대값이 크다고해서 두 변수간 관계가 강한 것 아닐 수 있음.
• -> 산점도와 상관계수의 수치를 함께 확인해야한다.
• 참고로 인과관계는 회귀분석에서 확인 가능.
• A와 B간 높은 상관관계가 산출되었다면,
  A가 B에 영향을 주는 경우, 그 반대의 경우
  A,B가 다른 하나 혹은 그 이상 요인으로부터 영향을 받는 경
  * 우연인경우
• 시계열자료, 독립적이지 않은 자료에 대해서는 상관계수 사용 적절하지 않음.