1. Perspective-n-Points

PnP problem이란?

• n개의 2D-3D correspondences가 주어졌을 때 world 좌표계에서 카메라 좌표계로의 transeformation을 추론하는 것.(estimate rigid body motion)

• 쉽게 말하면 카메라가 3D 월드를 바라보고 있을 때 이미지의 feature들과 3D-points 간의 correspondence를 알고 있다면 이를 기반으로 현재 카메라의 pose를 추정하는 것이다.

• PnP는 노이즈를 전혀 고려하지 않기 때문에 RANSAC 같은 outlier 제거 알고리즘이 필수적이다.

OpenCV에 있는 solvePnP() 함수

bool cv::solvePnP(InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, 
				  InputArray distCoeffs, OutputArrayrvec, OutputArray tvec,
                  bool useExtrinsicGuess = false, int flags = SOLVEPNP_ITERATIVE);

• 카메라 켈리브레이션 행렬을 알고 있어야 한다.

2. Minimal solver - P3P Grunert method

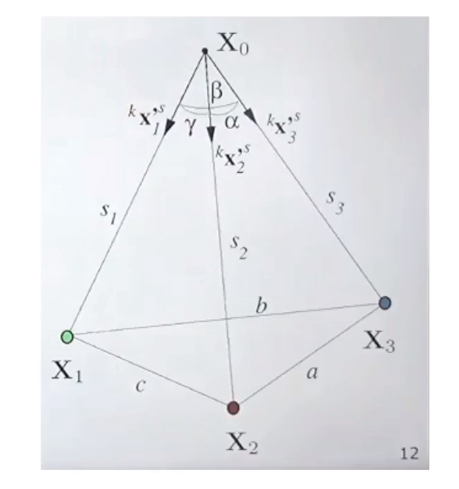
전제조건

• 3개의 3D-point X1, X2, X3와 각각에 대응되는 2D-point X^1, X^2, X^3를 알고 있다.
• 중점 X0로부터 3D-point까지의 거리는 모르는 상태다.

p3p 의 두가지 과정

• Estimate length of projection rays
• Estimation the orientation

step1 - Estimate length of projection rays

kXis는 ray의 방향을 나타낸 unit-vector이고 여기에 거리값 스칼라인 Si를 곱해준다.
Xi - Xo는 각각의 3D-point에서 중점까지의 거리를 나타내고 이를 3D-world -> camera 를 나타내는 Rotation matrix를 곱해 카메라 좌표에서의 ray의 길이를 나타낸다. 이 두개가 서로 같다는 것을 위 이미지에서 보이고 있다.

ray들의 길이를 구하기 위해 각 ray들이 이루는 각도를 구한다.

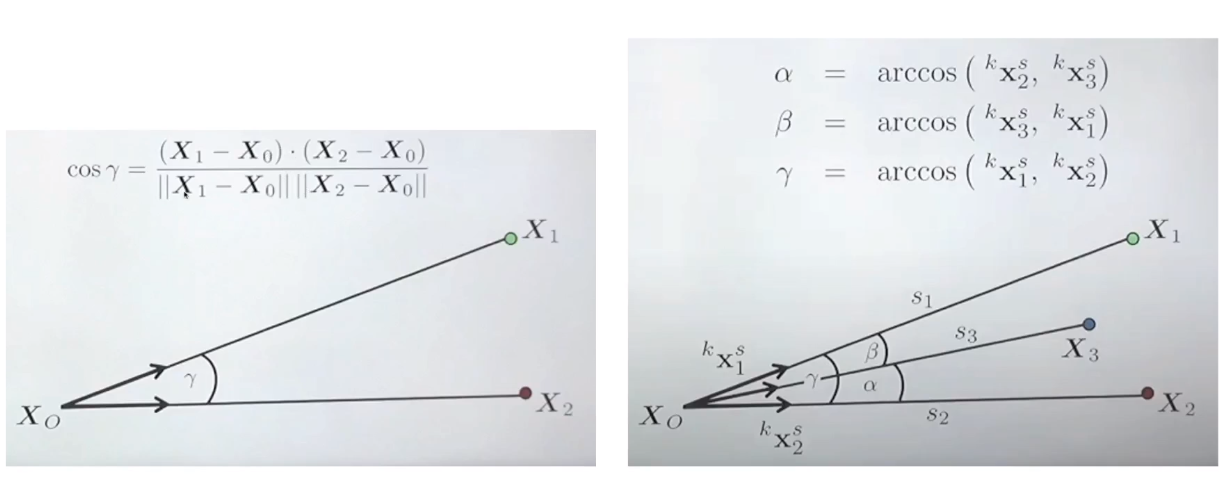
구한 각도들과 3D-points들 사이의 거리를 활용해 코사인법칙을 이용하여 다음과 같은 식을 만든다.

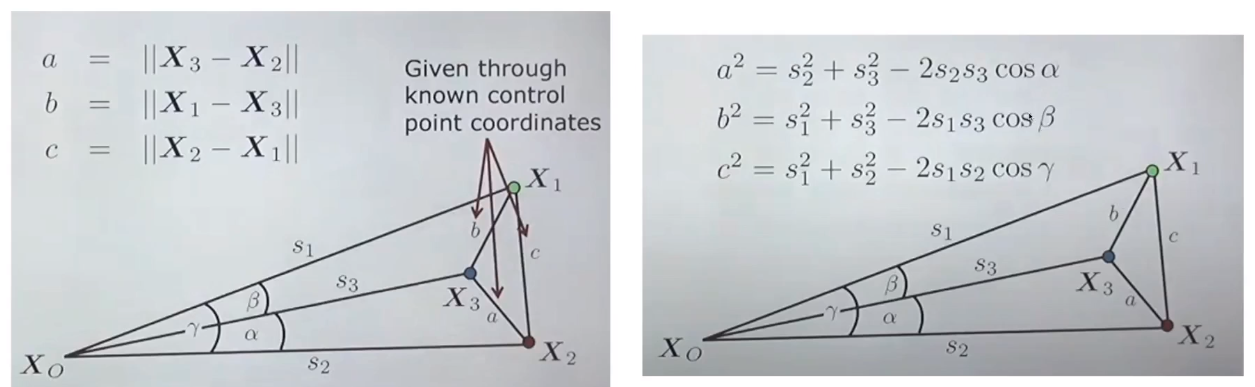
u와 v라는 변수를 설정하여 아래와 같이 식을 정리한다.

코사인법칙을 이용하면 s1^2을 표현할 수 있는 세가지 식이 나오고 이를 정리하면 u를 없애고 v만 남길 수 있다. 즉 v에 대한 4차식이 나오게된다.

v에대한 4차식에서 4개의 해가 도출되므로 이 중 카메라 좌표계에서 유효한 해가 무엇인지 선택하는 과정이 필요하다. 다른센서에서 가져온 orientation정보를 활용하거나 또다른 2d-3d correspondence를 가져와 orientation을 검증하는 방법이 있다.
두번째 방법은 하나의 correspondence를 추가하므로 p3p가 아니다. 요즘은 다양한 기하학적 방법론들을 통해 3개의 correspondence 만으로 카메라 pose를 추정하는 방법들이 제안되고 있다.