3D Rigid Body Motion

3D Rigid Body Motion: 3차원 좌표계의 변환을 의미

Pose = 카메라의 위치(Position) + 카메라가 바라보는 방향(Orientation)

• Position = {tx, ty, tz}
• Orientation = {Rx, Ry, Rz}
• 6 Degrees of Freedom = {tx, ty, tz, Rx, Ry, Rz}

다양한 Rotation 표현법

1. Axis-angle

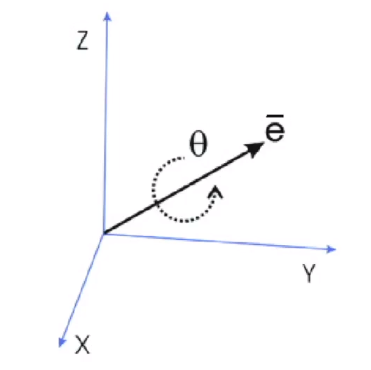
• Axis-angle = Angle-axis = Rotation vector = Rodrigues angle 다 같은말.
• 축의 방향을 가리키는 벡터와 회전각으로 구성.
• 파라미터 갯수가 적어 메모리 효율성이 좋음.
• Rodirgues formula( Axis-angle <-> Rotation matrix)
  

2. Quaternion

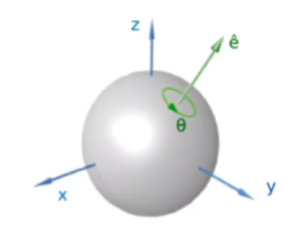
• 미분가능하며 singularity가 없어 김벌락 걱정이 없다.
• 4DOF representation{w,x,y,z}

3. SO(3) Rotation matrix

• 3축에대한 정보를 하나의 행렬에 모두 담음.
• 미분은 가능하나 파라미터가 많아(9개) 최적화가 불편하다.(Lie Algebra로 풀면 최적화 가능.)
  

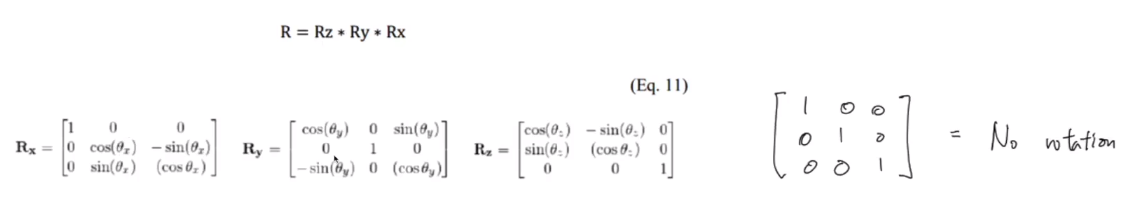
Transformation 표현

• 이동치 표현.
• vector{x,y,z}로 표현.

SE(3)

• SO(3) + Transformation
• Spetial Euclidean Group(3D)