[ML] 2편 - Linear tasks : classification(분류)-1.판별함수 접근법

재로미·2021년 1월 16일

Machine Learning

목록 보기

2/7

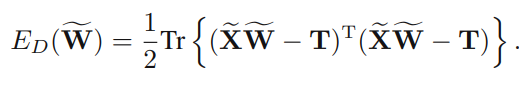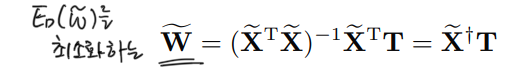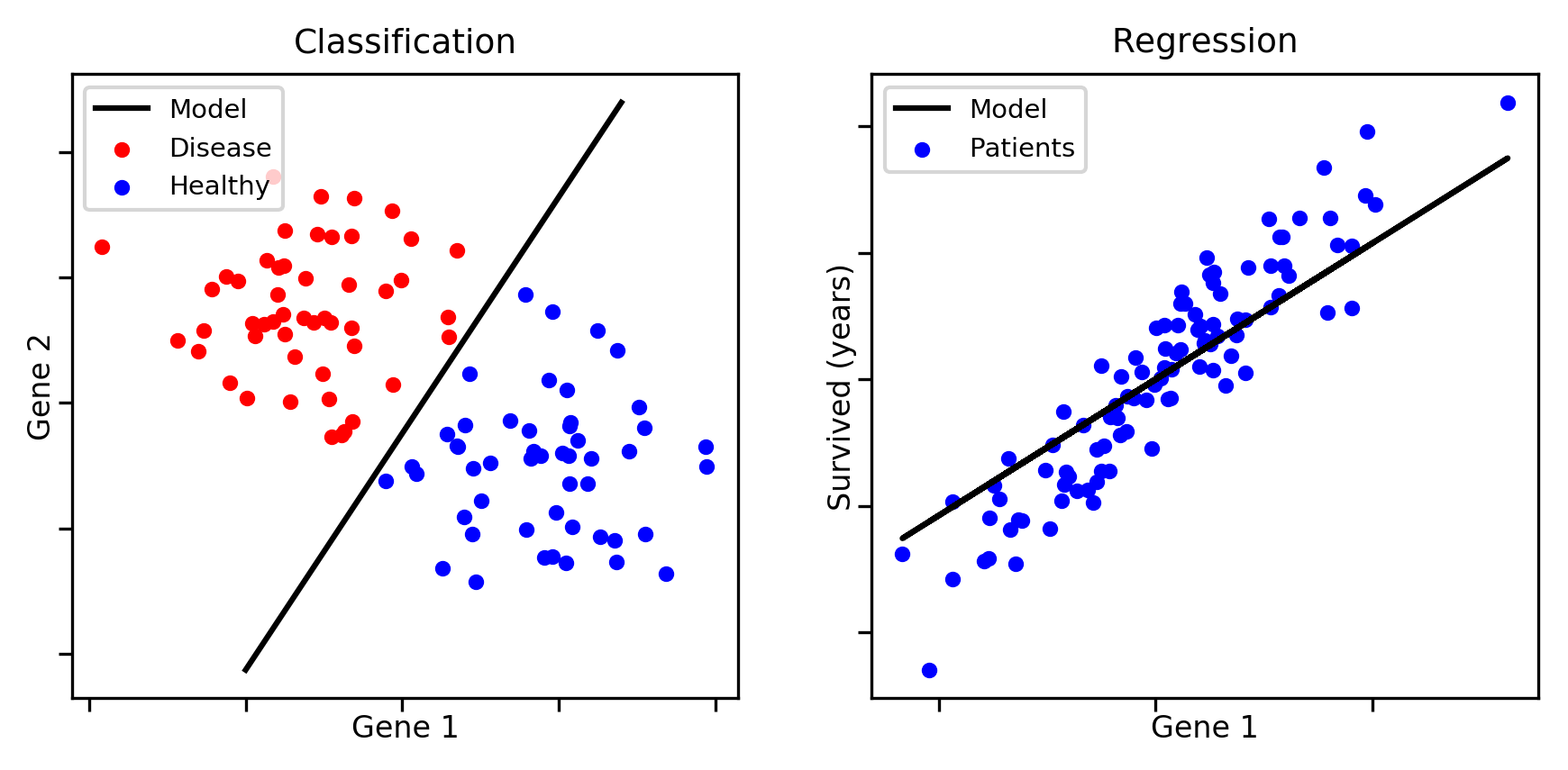
Supervised Learning methods

지난 1편에서 supervised learning과 unsupervised learning이라는 머신러닝 학습 종류가 있다는 것을 배웠다. 연구 분야, 프로젝트에 따라 다르지만 보통 주로 정답 label이 있는 supervised learning, 지도학습을 많이 사용하는데, 이번 편에서는 지도학습 방법론 중에 linear한 데이터를 다루는 모델들을 살펴보자.

Linear tasks

먼저 linear 의 의미는 간단하게는 '선형성'이라는 우리말로 표현된다. 수학 개념상 직선을 가리키는 말이지만, 우리가 선형이라고 부르는 수식들의 특징은 직선 방정식에서 중첩의 원리(superposition principle)가 적용된다는 것이다. 성돌의 전자노트 라는 블로그에서 성돌 님의 말을 인용하자면 다음과 같이 중첩의 원리를 설명할 수 있다.

$y = ax$ 라는 직선의 방정식이 있을 때 서로 다른 입력값인 $x_1$ 과 $x_2$ 를 함수에 대입했을 때 구해지는 함수값은 각각 $ax_1$ 과 $ax_2$ 이다. 이 때, $x_1+x_2$ 의 함수값은 $a(x_1+x_2)$ 로 $x_1$ 와 $x_2$ 의 함수값을 각각 구하고 더해준 $ax_1+ax_2$ 값과 동일하다.

당연하게 느껴지는 말인데 이게 중첩의 원리이며 곧 선형성, linear를 표현하는 말이 된다. 한 함수값을 다른 여러개의 함수값의 합으로 표현할 수 있고 이를 통해 어느 정도 예측이 가능한 결과값으로 표현가능한 것이 핵심이다. 머신러닝, 나아가 딥러닝에서는 이 linear 개념이 정말 정말 많이 쓰이고 있으며, 행렬과 벡터를 주로 다루는 수학의 한 분야인 선형대수학과 깊이 연관이 되어 있어, 아직 공부를 하지 않은 사람이라면 선형대수학(linear algebra)공부도 같이 할 것을 적극 권장한다. 참고로 비선형(non-linear)문제는 앞서 언급한 중첩의 원리가 통하지 않기 때문에 이를 해석하기 힘들어서 어려운 것으로 간주된다.

지도학습 머신러닝 모델에서 linear한 task를 가진다고 할 때 아래와 같이 크게 두가지 문제로 나눌 수 있다. classification과 regression 이 되며, 이 두 가지가 linear한 특성을 지니면 공통적으로 아래 수식을 갖는다.

\hat{y_j} = f_j(x) = w_{1j}x_1 + w_{2j}x_2 + \cdots + b_j = \Sigma_i{w_{ij}x_i} + b_j

선형대수학을 배운 사람이라면 바로 이해하는 대표적인 일차방정식의 수식으로, $w_{ij}$ 는 weight vector(가중치 벡터), $x_i$ 는 input feature(입력값), $b_j$ 는 원점으로 부터 얼마만큼 떨어져있는지를 나타내는 절편 즉 bias(오차, 편향)를 의미한다. 이 가중치 벡터들과 입력값의 합은 곧 행렬이 되어(*수식을 세우는 것에 따라 가중치 벡터 합에 transpose를 시켜야 할 수도 있다) 행렬의 linear combination으로 나타낼 수 있다는 특징을 갖는다는 것 정도만 이해하고 넘어가자. 이제 부터는 선형대수학 개념이 많이 나와 선형대수학을 공부하지 않았다면 직관적으로 이해하기 어렵기 때문에 꼭 공부를 하고 읽는 것을 추천한다.

linear classification 전체를 한꺼번에 다루기에는 양이 방대하여 본 편에서는 classification 중 판별함수를 이용하여 분류하는 방법에 대해 살펴보겠다.

Linear classification

먼저, classification은 분류라는 뜻이며 지난 편에서도 언급을 하였듯, label이 예/아니오, 0/1로 나뉘는 이진 문제나 어떤 특정 범주가 있는 categorical한 문제에 주로 적용되는 머신러닝 방법론이다.

f_j(x) = \Sigma_i{w_{ij}x_i} + b_j

앞서 다룬 수식은 class j 에서의 판별식으로 정의 될 수 있으며, 이는 아래 그림이 있을 때 각각을 구분 짓는 직선들을 의미한다.

분류 문제의 주된 목적은 입력 벡터 $\mathrm{x}$ 를 1~ $\mathrm{K}$ 개의 상호 배타적(mutual exclusive) 클래스 중 하나로 구분지어 할당하는 것이다. 그림과 같이 입력 벡터가 어떤 입력 공간을 그리게 되면 이 영역을 decision region이라고 하며, 이 경계이자 직선방정식을 결정 경계면이라고 한다. 머신러닝에서, 이러한 분류 문제를 해결하기 위한 확률적 모델로는 크게 판별함수 접근법, 확률적 생성 모델법, 확률적 식별모델법 이렇게 세 가지 정도가 있는데, 판별 함수를 사용하여 접근하는 것이 가장 간단하다.

확률적 모델(probablistic model)

생성 모델(generative model) : $p(\bold x|C_k)$ 와 $p(C_k)$ 를 모델링한 다음 베이즈 정리(Bayes Theory)를 사용해서 클래스의 사후 확률 $p(C_k|\bold x)$ 를 구하거나 직접 결합확률 $p(\bold x, C_k)$ 를 모델링할 수도 있음
식별 모델 (discriminative model) : $p(C_k|\bold x)$ 를 직접적으로 모델링함
판별 함수 (discriminant function) : 입력 $\bold x$ 을 클래스로 할당하는 판별함수(discriminant function)를 찾는다. 이 때, 확률값은 계산하지 않는다.

본 편에서는 판별 함수 접근법만 다루기로 하였으니 판별함수 분류 결정 이론 은 다음과 같이 정의 된다.

판별함수 (Discriminant Functions)

2개의 클래스 문제로 가정할 때, 결과변수 $y(\bold x) \ge 0$ 이면 이를 $C_1$ , 아닌 경우 $C_2$ 로 판별함

결정 경계면 (Decision boundary)

이 때의 결정 경계면은 $y(\bold x)=0$ 일 때 이고,

$\bold x$ 가 $D$ 차원의 입력벡터일 때 $D-1$ 차원의 hyperplane임

$D=2$ 일 때, 임의의 두 점 $\bold x_A, \bold x_B$ 가 결정 경계면 위에 있다고 하자. 이 때 $y(\bold x_A)=y(\bold x_B)=0$ 를 만족하고, 이는 $\bold w^T(\bold x_A-\bold x_B)=0$ 역시 만족하여 $\bold w$ 는 결정 경계면에 orthogonal(수직)한 것을 알 수 있다. 위 그림에서 $\mathcal{R_1, R_2}$ 는 결정 영역으로, $y \gt 0$ 이면 $\mathcal{R_1}$ 으로 할당함을 의미한다. 빨간색 선으로 나타난 결정 경계면에서의 식을 전개하면 다음의 식을 도출할 수 있다. 이 때 $||\bold w||$ 는 norm이라고 읽으며, 벡터 $\bold w$ 의 길이(크기)이다.

임의의 한 점 $\bold x$ 로 부터 결정 경계면에 수직으로 내린 지점을 $\bold x_{\perp}$ 라고 하자. 이 때 아래와 같은 식을 도출하여 성립함을 알 수 있다. (아래 식에서 $\bold x_{\perp} = \bold x_p$ 이고, $r$ 은 결정계수이다. )

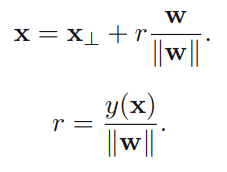
이를 통해 궁극적으로 알 수 있는 것은

$w_0 \lt 0$ 이면 결정 경계면은 원점으로부터 $\bold w$ 가 향하는 방향으로 멀어져있다.

$w_0 \gt 0$ 이면 결정 경계면은 원점으로부터 $\bold w$ 의 반대 방향으로 멀어져있다.

$y(\bold x) \gt 0$ 이면 $\bold x$ 는 결정 경계면을 기준으로 $\bold w$ 가 향하는 방향에 있다.

$y(\bold x) \lt 0$ 이면 $\bold x$ 는 결정 경계면을 기준으로 $-\bold w$ 가 향하는 방향에 있다.

$y(\bold x)$ 의 절대값이 클 수록 더 멀리 떨어져 있다.

위에서 다룬 것들은 클래스의 개수가 2일 때 였는데, 그렇다면 클래스 수가 2보다 클 때는? 이 때는 이진 클래스 문제를 여러개 조합해서 해결할 수도 있고, 최소제곱법, 퍼셉트론 알고리즘을 통해 접근할 수 있다. 그렇게 접근했을 때 위와 같은 K-class boundary를 그릴 수 있으며, 녹색으로 표시된 영역은 판별할 수 없는 영역이다. 이진 클래스를 이용했을 때는 결정 구역은 단일 연결(singly connected)로 이루어지며 그 모양은 볼록(convex)하게 나타난다. 초록색으로 칠해진 판별 불가한 영역도 해결하는 공식이 있는데 아래 식이 그것이다. 여기서 $k$ 는 $1, ..., K$ 의 값을 가지고, 이런 판별식을 사용하는 경우 $j\not=k$ 일 때 $y_k(\bold x)\gt y_j(\bold x)$ 를 만족하면 $\bold x$ 를 클래스 $C_k$ 로 판별하게 된다.

dummy input 값으로 $x_0 = 1$ 을 넣어 수식을 단순화 하면,

$\tilde{\bold w} = (w_0, \bold w)$ [행렬 $\tilde{\bold w}$ 를 사용했을 때]

$\tilde{\bold x} = (x_0, \bold x)$

$y(\bold x) = \tilde{\bold w}^T\tilde{\bold x}$ , 여기서 $\tilde \bold W$ 의 $k$ 번째 열 $\tilde{W}_k=(w_{k0}, \bold w_k^T)^T$

최소제곱법(Least Squared Method)

제곱합 에러 함수
학습데이터 ${\bold x_n, \bold t_n}, n = 1, \dots, N, n$ 번째 행이 $\bold t_n^T$ 인 행렬 $\bold T$ , $n$ 번째 행이 $\tilde{\bold x}_n^T$ 인 행렬 $\tilde{\bold X}$ 가 주어졌을 때 제곱합 에러함수는 다음과 같이 표현할 수 있다.
이를 정리하면 제곱합 에러함수를 통해 판별함수를 다음 공식으로도 표현이 가능하다. 이것이 최소제곱법을 분류에 적용했을 때의 개념인데, 이 방법도 두가지 단점이 있다.

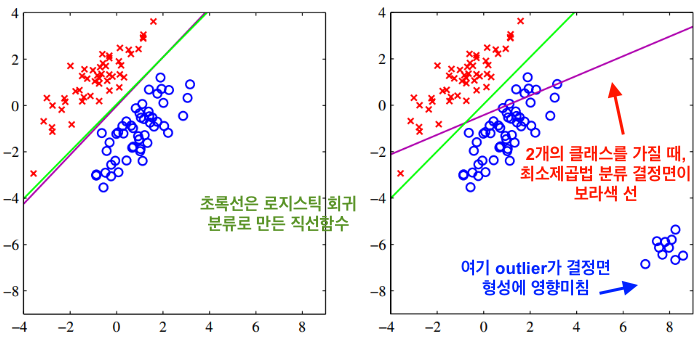
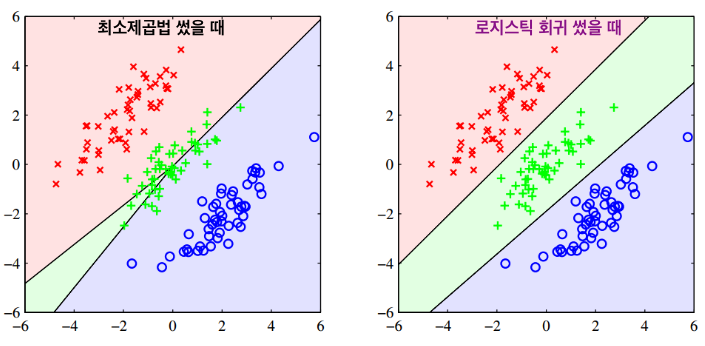
최소제곱법의 단점

outlier 데이터에 민감함 -> outlier 데이터에 영향을 아래와 같이 받아 에러함수가 달라짐

목표값의 확률 분포가 가우스 분포가 아니면 분류가 부정확함

퍼셉트론(Perceptron) 알고리즘

앞서 다룬 선형 분류의 기본공식은 직선 방정식의 형태를 가진다고 하였다. 해당 수식을 neural network(신경망) 개념과 연관 지었을 때 다음 처럼 나타낼 수도 있다. 여기서 $f$ 는 활성화 함수(Activation function)라고 하여 퍼셉트론은 아래와 같은 계단형 함수를 사용하며 이 때의 $\phi_0(\bold x)=1$ 이다.
* 퍼셉트론 알고리즘의 에러 함수
여기서 $\mathcal{M}$ 은 잘못 분류된 데이터들의 집합을 의미한다. 경사하강법(Stochastic gradient descent)를 적용하면 퍼셉트론은 다음 수식을 가지며, 가중치 업데이트가 실행되면서 잘못 분류된 샘플 $\mathcal{M}$ 에 미치는 영향을 반영하면, 위 수식은 또 다시 과정을 거쳐 업데이트를 거친 가중치에 대한 에러는 이전 단계( $\tau$ )에서의 에러보다 줄어들게 된다. 퍼셉트론 알고리즘 수식 적용 과정을 그래프로 나타내면 다음과 같다. 검은색 선이 결정 경계 hyperplane이고 검은색 화살표가 $\bold w$ 가중치 벡터를 가리킨다. 이렇게 가중치를 수정해가며 최적의 결정경계면을 찾는 과정을 보아 퍼셉트론 알고리즘을 통한 분류가 최소제곱법식 분류보다는 좀 더 좋은 알고리즘이라고 생각할 수 있다.

분류 1편 - 판별함수 접근법을 마치며

이렇게 선형 분류를 위한 확률적 모델법 중 판별함수를 이용한 분류 접근법과 이를 뒷받침하는 두가지 알고리즘인 최소제곱법과 퍼셉트론 알고리즘 에 대해 알아보았다. 수식들이 워낙 많고 익숙하지 않아서 이해하기 어려웠을 것이라 생각한다. 나 역시도 이를 완벽하게 소화해내지는 못하여서 두고 두고 복습하려고 이렇게 정리하는 것도 있다. 그러나 머신러닝 이론적으로 분류 배경에 관해 잘 알아 놓을 필요는 있기 때문에 이것들을 잘 이해 해 놓는 것이 중요하다. 다음 편에서는 확률적 생성모델과 확률적 식별모델에 대해 공부해보자.

본 포스트는 leeyongjoo님이 작성한 포스트를 많이 참고하여 이를 이해하고 약간의 가공을 거쳤음을 밝힙니다.