[ML] 3편 - Linear tasks : classification(분류)-2. 생성모델, 식별모델 접근법

재로미·2021년 1월 19일

Machine Learning

목록 보기

3/7

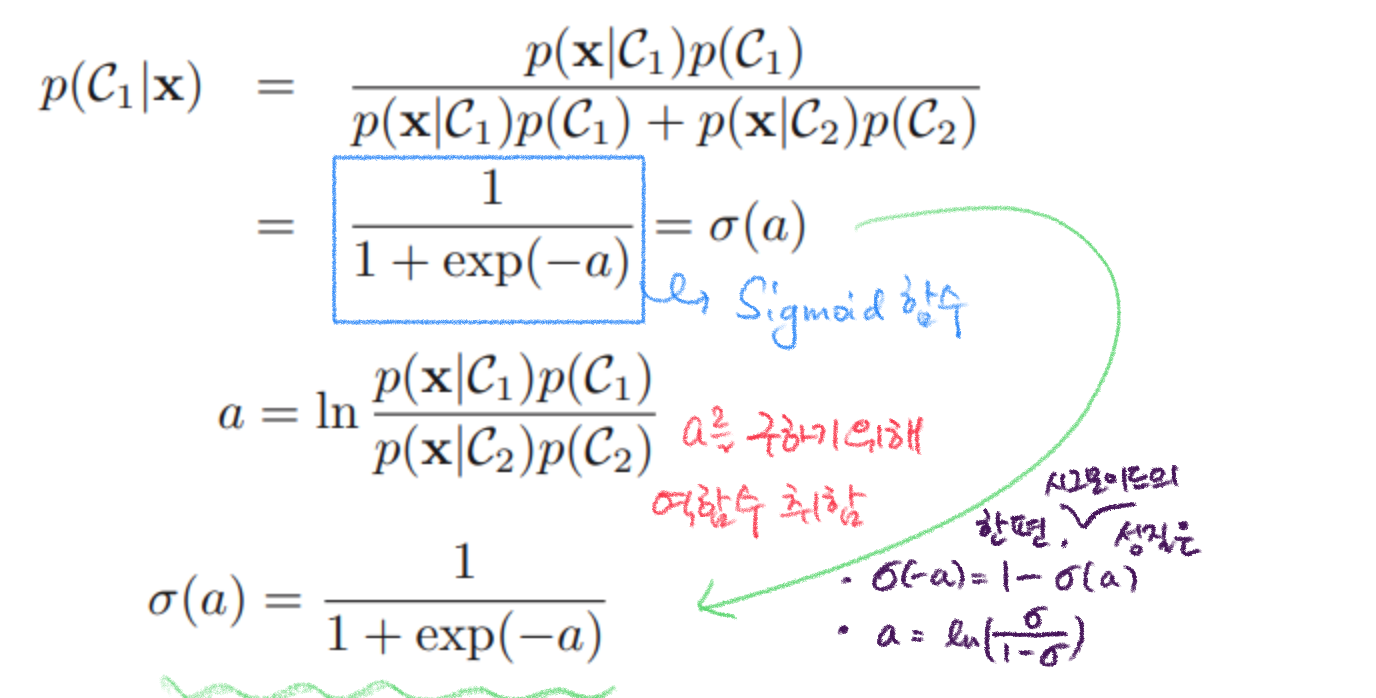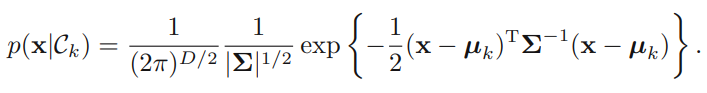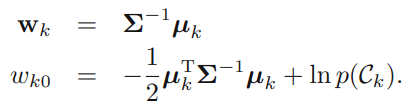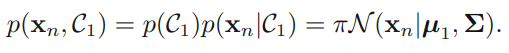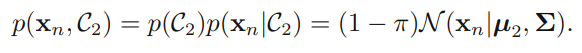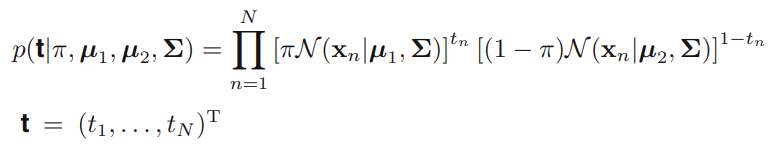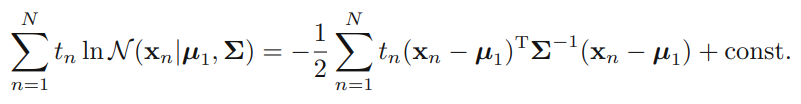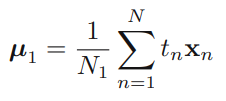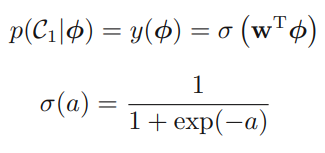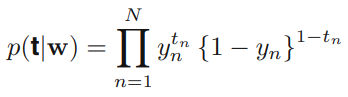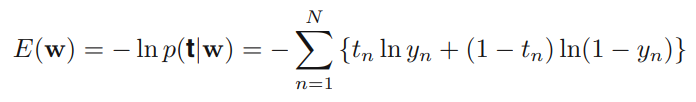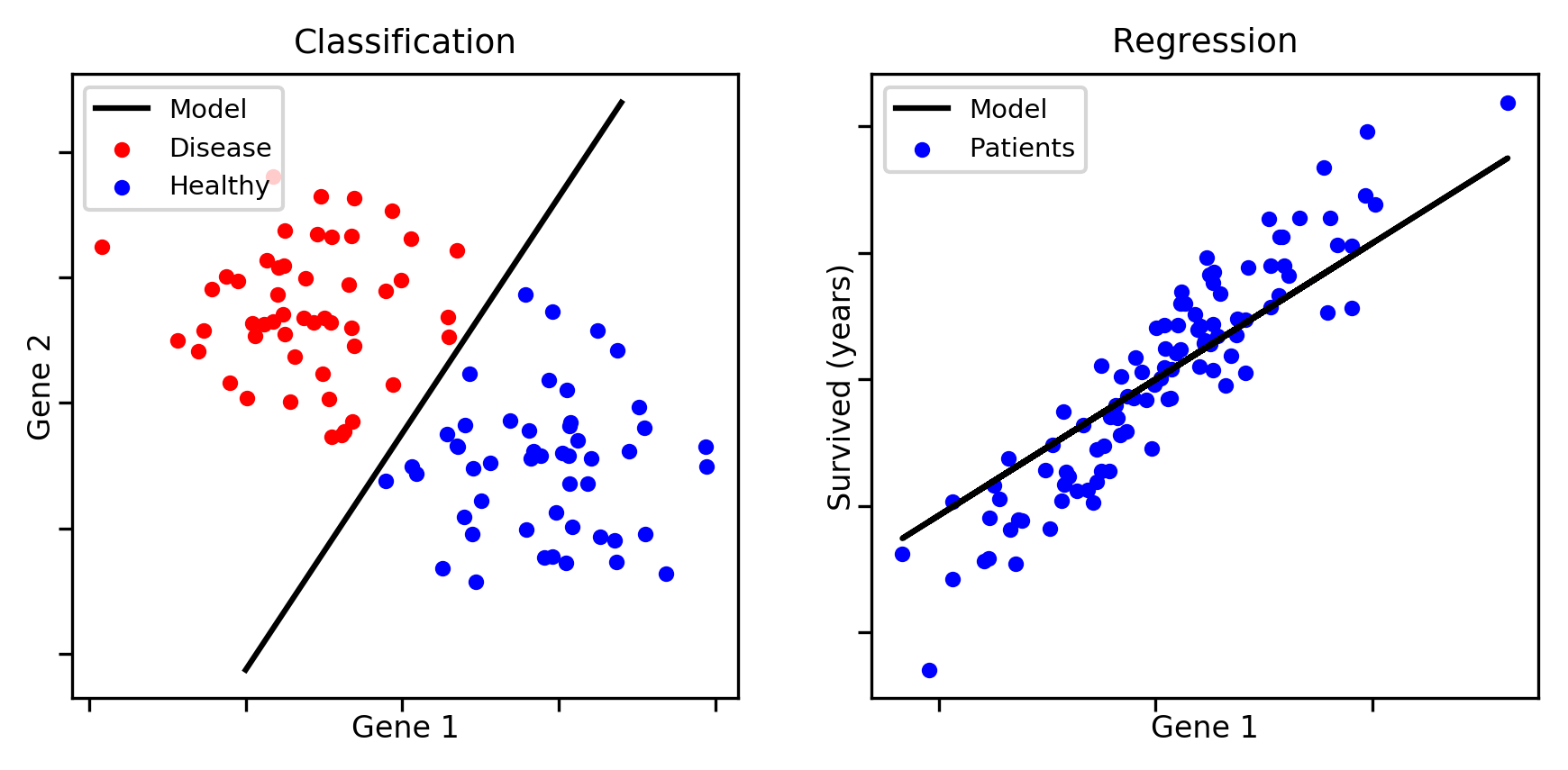
Classification (cont.)

분류-1 복습(Revisit)

2편에 이어 3편에서도 선형 데이터 처리의 일종인 선형 분류(Linear classification)에 대해 알아보려고 한다. 지도학습 머신러닝 모델에서는 linear task를 다룰 때 공통적으로 다음 수식을 가진다고 지난 포스트에서 언급을 했었다.

$\hat{y_j} = f_j(x) = w_{1j}x_1 + w_{2j}x_2 + \cdots + b_j = \Sigma_i{w_{ij}x_i} + b_j$

혹시 이 수식이 낯설다면 여기를 클릭하여 한번 탐구하고 넘어오길 바란다. 분류의 확률적 모델에는 다음과 같이 판별 함수형태, 생성모델, 식별모델 이렇게 세가지가 있다고 언급하였다.

확률적 모델(probablistic model)

생성 모델(generative model) : $p(\bold x|C_k)$ 와 $p(C_k)$ 를 모델링한 다음 베이즈 정리(Bayes Theory)를 사용해서 클래스의 사후 확률 $p(C_k|\bold x)$ 를 구하거나 직접 결합확률 $p(\bold x, C_k)$ 를 모델링할 수도 있음
식별 모델 (discriminative model) : $p(C_k|\bold x)$ 를 직접적으로 모델링함
판별 함수 (discriminant function) : 입력 $\bold x$ 를 클래스로 할당하는 판별함수(discriminant function)를 찾는다. 이 때, 확률값은 계산하지 않는다.

이번에는 아직 다루지 않은 나머지, 생성모델과 식별모델 접근법에 대해서 공부해보자. 시작하기에 앞서, 본 편은 베이즈 정리와 조건부 확률 등 통계학적 개념이 많이 나오기 때문에 이러한 용어들이 익숙하지 않다면 역시 이해하기 어려울 수 있다.

생성 모델(generative model)

분류 문제를 확률적 관점에서 바라보았을 때, linear regression(선형 회귀, 다음 편에서 다룰 예정)과 마찬가지로 확률적 모델은 통합적인 관점으로 접근할 수 있도록 도와준다.

생성 모델 접근법에서는 데이터의 분포에 관해 어떤 가정을 두고, 적절한 과정을 거쳐 선형적인 결정 경계면(linear decision boundary)을 유도한다. 앞서 특정하였듯, 입력 $\bold x$ 에 대해 $p(\bold x|C_k)$ 와 $p(C_k)$ 를 모델링한다음 베이즈 정리를 사용해서 클래스의 사후 확률 $p(C_k|\bold x)$ 를 구한다.

분류 1편의 판별 함수 방법에서는 최소제곱법이나 퍼셉트론 알고리즘의 에러함수를 최소화시키기 위한 최적의 파라미터를 찾는 것이 목적이었다면, 확률적 모델은 데이터의 분포(클래스 포함) 를 모델링하면서 분류 문제를 풀 수 있는 방법을 제시한다.

$p(C_k|\bold x)$ 를 구하는 공식은 다음과 같이 전개 된다. $k$ 는 해당 클래스의 넘버이다.
만약 클래스의 개수가 2 개보다 많을 때 $p(C_k|\bold x)$ 는 이렇게 된다. 그럼 데이터 입력 $\bold x$ 가 연속한 입력일 때는 어떻게 될까?

입력이 연속일 때 (Continuous inputs)

_
$p(\bold x|C_k)$ 가 가우시안 분포를 따르고 모든 클래스에 대해 공분산(covariate)가 일정하다고 가정했을 때 수식은 위처럼 세울 수 있으며, $a$ 를 $\bold x$ 에 관한 선형방정식으로 다음과 같이 정리할 수 있다.
만약 클래스의 개수가 $K$ 개 이면, $\bold x$ 와 $w_0$ 는 다음과 같이 바뀌게 된다.

입력이 이산적일 때 (Discrete inputs)

각 특성 $x_i$ 가 0과 1 둘 중 하나의 값을 갖고 클래스가 주어졌을 때 특성(feature)들이 조건부독립(conditional independence)이라는 가정을 할 경우 문제는 단순화된다. 이러한 가정을 나이브 베이즈(Naive Bayes) 가정이라고 하며, $p(\bold x|C_k)$ 식은 다음과 같이 형성된다. 이를 $a$ 에 관한 식으로 다시 정리하면 (시그모이드 성질 이용),

$a_k(\bold x) = \ln p(\bold x|C_k)p(C_k)$ , 최종적으로
와 같은 식으로 분류할 수 있다.

최대 가능도(우도) 해(Maximum Likelihood Solution) 사용

먼저 가능도라는 개념에 대해 살펴보자.

가능도는 '우도'라는 표현으로 많이 알려져있으며, 영어로는 likelihood이다. 이 가능도는 확률과 깊은 연관을 갖는데, 먼저 확률(Probability)은 주어진 모델 모수(parameter) 값과 어떠한 관측치에 대한 참조 없이, 랜덤 출력에 대한 일어날 뻔한 가능성이며 동전 던지기에서의 앞면이 나올 가능성을 예로 들 수 있다. 가능도는 어떤 확률 변수 $X$ 가 모수 $θ$ 에 대한 확률 분포 $P_θ (X)$ 를 가지며, $X$ 가 특정한 값 $x$ 로 표본 추출 되었을 때 모수 $θ$ 에 대한 가능도 함수는 다음과 같이 정의 되며, $θ$ 가 전제 되었을 때 sample $x$ 가 등장할 확률에 비례한다.
$L(θ│x)=P(X=x|θ)$
가능도는 주어진 특정한 관측치를 기반으로 하여 어떤 모델의 모수가 될 뻔한 가능성이며, 셀 수 있는 사건들에서는 확률과 가능도가 같지만, 연속적인 사건들에서는 확률밀도함수(Probability Density Function;PDF)가 가능도가 된다. 가능도 함수(Likelihood function)은 확률 분포가 아니므로, 확률의 성질과 달리 가능도를 전부 합해서 1이 되지 않을 수 있으며, 정규분포부터 회귀분석과 오늘날의 인공지능 알고리즘에 이르기까지 통계학적으로 많이 사용되는 개념이다.

이 가능도를 최대화한 것이 최대가능도 = 최대우도 라고 하며, 영어로는 MLE(Maximum Likelihood Estimator)라고 한다. 이 최대우도해를 이용해 확률적 생성 분류 모델의 파라미터를 구하면, 이진 클래스 문제에서:

Data inputs: $\{ \bold x_n, t_n \}$

$n=1,\dots,N$

$t_n=1$ -> $C_1$ 분류 | $t_n=0$ -> $C_2$ 분류

Likelihood equation :

If $t_n=1$ ,

If $t_n=0$ ,

Equation

Parameters: $p(C_1)=\pi$ 라고 두면, $\bold \mu_1, \bold \mu_2, \Sigma, \pi$ 구해야함

$\tau$ 구하기
로그우도 함수(Log-likelihood function)에서 $\tau$ 관련한 항들을 모으면 위 식과 같이 되고, 이를 $\tau$ 에 대해 미분하고 미분값을 0으로 놓고 풀면, 위와 같이 간단히 나타낼 수 있다. 이 때, $N_1$ 은 $C_1$ 에 속하는 데이터 표본의 수이고, $N_2$ 는 $C_2$ 에 속하는 표본의 수이다.

$\bold \mu_1, \bold \mu_2$ 구하기
$\tau$ 구하기와 유사하다. $\bold\mu_1$ , $\bold\mu_2$ 각각 관련항들을 다음 식처럼 정리하고 이 식을 각각의 $\mu_1$ , $\bold\mu_2$ 에 대해 미분한 다음 0으로 놓고 풀면,
이렇게 식을 도출할 수 있다.

$\Sigma$ 구하기
위에서 $\tau$ , $\bold \mu_1, \bold \mu_2$ 구한 것 처럼 $\Sigma$ 관련항들을 묶어 이를 미분하여 식을 구하면, $\bold S$ 에 관한 term들이 나오는데 가우시안 분포의 MLE 구하는 방법을 그대로 적용하면 최종적으로, $\Sigma = \bold S$ 가 되어 $\Sigma$ 역시 구할 수 있다.

이렇게 확률적 생성모델에 대해 알아보았다. 생성모델이 베이즈 정리를 사용하기 위해 $p(\bold x|C_k)$ 와 $p(C_k)$ 를 모델링 하여야 했다면, 확률적 식별 모델은 $p(C_k | \bold x)$ 를 직접 모델링하는 것이다.

식별 모델(Discriminative model)

생성모델에서 sigmoid 함수를 이용해, 클래스의 개수 $K$ 가 2일 때, $p(C_k | \bold x)$ 를 아래와 같이 접근할 수 있으며,

p(C_1|\bold x)=\sigma(\bold w^T\bold x+w_0)

이를 최대우도추정법으로 확률분포들 $p(\bold x|C_k), p(C_k)$ 의 파라미터들을 구하여 $\bold w$ 와 $w_0$ 의 값을 구하는 것을 다뤘다. 식별 모델에서는 입력벡터 $\bold x$ 대신 비선형 기저함수(basis function)들 $\phi(\bold x)$ 를 사용하여 $p(C_k|\bold x)$ 를 $\bold x$ 에 관한 함수로 파라미터화 시키고 이 파라미터들을 직접 MLE를 통해 구하는 것을 보인다. 이 때 사용되는 것이 로지스틱 회귀인데, regression이라고 해서 회귀가 아니고, 이름과 달리 분류와 더 관련이 깊은 방법임을 참고하면 좋겠다.

로지스틱 회귀(Logistic Regression)

클래스 $C_1$ 의 사후확률은 특성벡터 $\phi$ 의 선형함수가 logistic sigmoid를 통과하는 함수로 위와 같이 표현되며, $\phi$ 가 $M$ 차원이라면 구해야 할 파라미터 ( $\bold w$ )의 개수는 $M$ 개이다. 생성모델에서는 $M(M+5)/2 + 1$ 개의 파라미터를 구해야 했는데에 비해 미지의 파라미터 수가 많이 줄었다.

로지스틱 회귀의 최대가능도 함수

Dataset: $\{\phi_n, t_n\},n=1,\dots,N$

$t_n\in{0,1}$

$\bold t=(t_1,\dots,t_N)^T$

$\phi_n=\phi(\bold x_n)$

$y_n=p(C_1|\phi_n)$

이 때의 Negative Log-likelihood 함수 == 크로스 엔트로피 에러함수

$y_n=\sigma(a_n), a_n=\bold w^T\phi_n$

Definition of Cross Entropy Error function

$H(p, q) = -\mathbb{E_p}[\ln q]$

$H(p,q)=-\sum_xp(x)\ln q(x)$ , 이산 확률변수일 때

일반적으로 크로스 엔트로피를 최소화할 수록 두 확률분포의 차이도 최소화됨

이는 likelihood 를 최대화 시키는 것,

모델의 예측값과 타겟변수의 차이 최소화 와 같은 말

분류 단원을 마무리하며...

원래는 이렇게 깊게 다루지 않고 분류가 뭔지 간략하게만 다루고 넘어가려고 했는데 자료를 찾아보니 생각보다 모르고 넘어가는게 너무 많았고, 그런 부족한 지식도 메우려는 욕심에 스케일이 조금은 커졌다. 지난 학기 수업 때 배운 분류 개념보다 한층 더 깊게 공부하게 되었지만, 머신러닝과 데이터 사이언스 공부를 하고 있는 내게 이정도 지식은 필요하다고 생각한다. 이 다음으로는 regression에 대해 다루고(regression도 classification 만큼 깊게 다룰지 모르겠다), ensemble을 다룰까 한다. 갓 배운, 그리고 여전히 배우고 있는 머신러닝을 나뿐만 아니라 다른 사람들도 이해할 수 있게 정리해나간다는게 결코 쉽지 않은 것 같다. 그렇다보니 집필 순서를 어떻게 해야할지, 실습은 어떻게 다룰 지 막막하지만 시간이 허락되는대로 꾸준히 해봐야겠다.

이번 분류 포스트들을 다루는데에 있어 leeyongjoo님의 블로그의 도움을 많이 받았음을 밝힙니다. 짤막한 글로나마 감사함을 남깁니다.