[ML] 4편 - Linear tasks : Regression(회귀)-1.최대가능도, 최소제곱법

재로미·2021년 1월 27일

Machine Learning

목록 보기

4/7

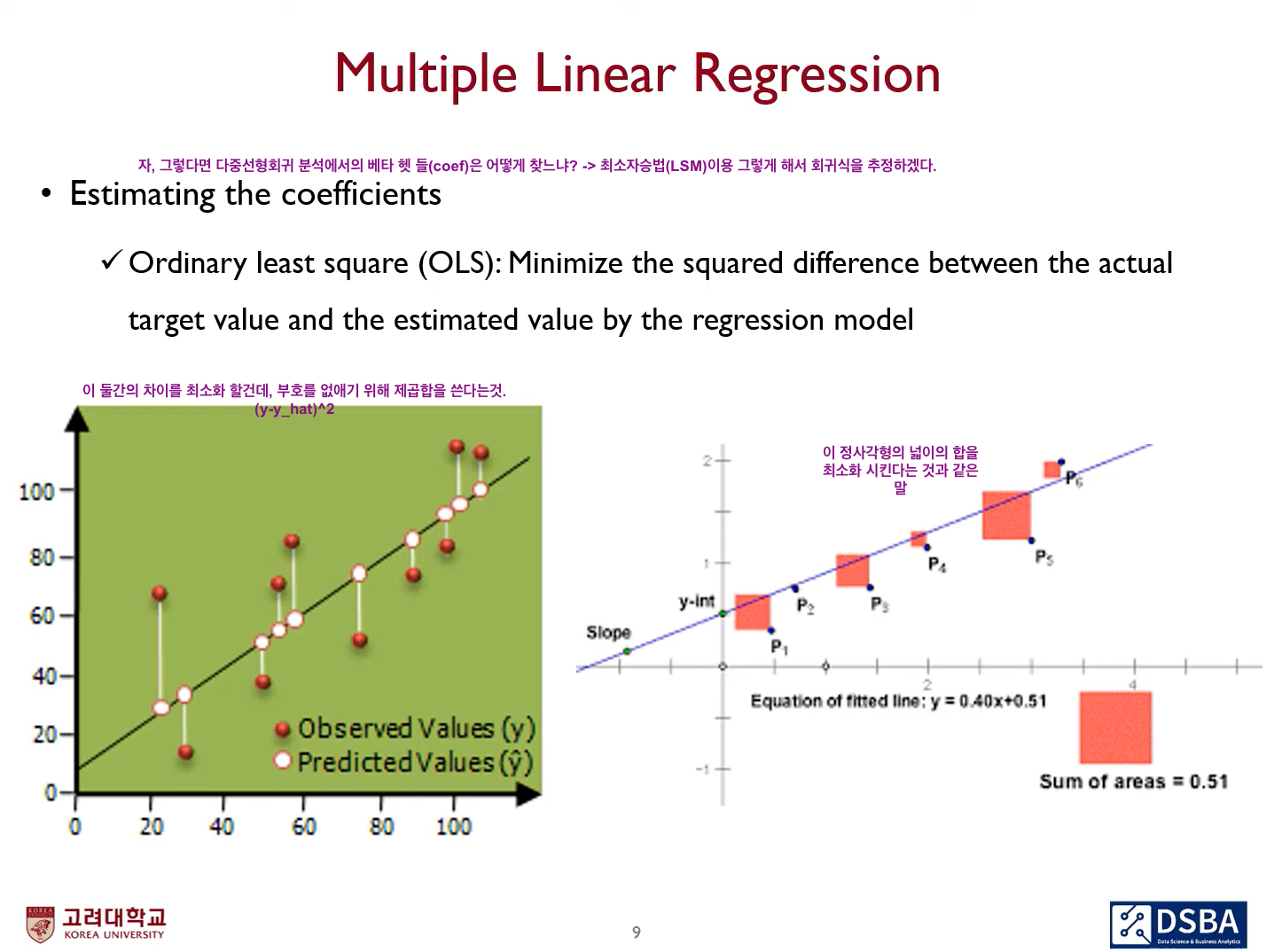
Regression

지난 포스트에서는 분류(classification)를 다뤘고, 이번에는 Regression이라고 하는 회귀분석에 대해 알아보자. 보통 회귀를 먼저 다루고 분류를 소개하는데, 분류와 회귀를 관통하는 키워드만 잘 알고 있으면 순서는 크게 상관이 없기에 회귀를 분류 다음으로 배치하였다.

회귀란?

대학에서 통계학 과목을 들을 때 보통 확률에 대해 배우고 난뒤, 가설검정과 표본 추정에 대해 학습을 한 후 좀 더 나아가 선형회귀분석(linear regression analysis)에 대해 배우게 된다.

회귀분석은 주어진 데이터의 변수들 사이에 함수 관계를 파악하여 이를 관통하는 하나의 식으로 세워 통계적 추론을 하는 분석법이다. 다른 말로 독립변수에 대한 종속변수의 평균을 구하는 방법이라고 하며, 이를 좀 더 고급지게 풀어설명하면 수치형 설명변수 X와 연속형 숫자로 이뤄진 종속 변수 Y간에 선형 관계가 성립한다고 할 때 이를 가장 잘 표현할 수 있는 회귀계수를 추정 하는 모델 이라고 할 수 있겠다. [bangu4's blog post , ratsgo's blog post]

선형 분류와 마찬가지로 회귀에서 핵심이 되는 수학적 수식은 다음과 같다.

$\hat{y_j} = f_j(x) = w_{1j}x_1 + w_{2j}x_2 + \cdots + b_j = \Sigma_i{w_{ij}x_i} + b_j$

IMG Source from JMP.com

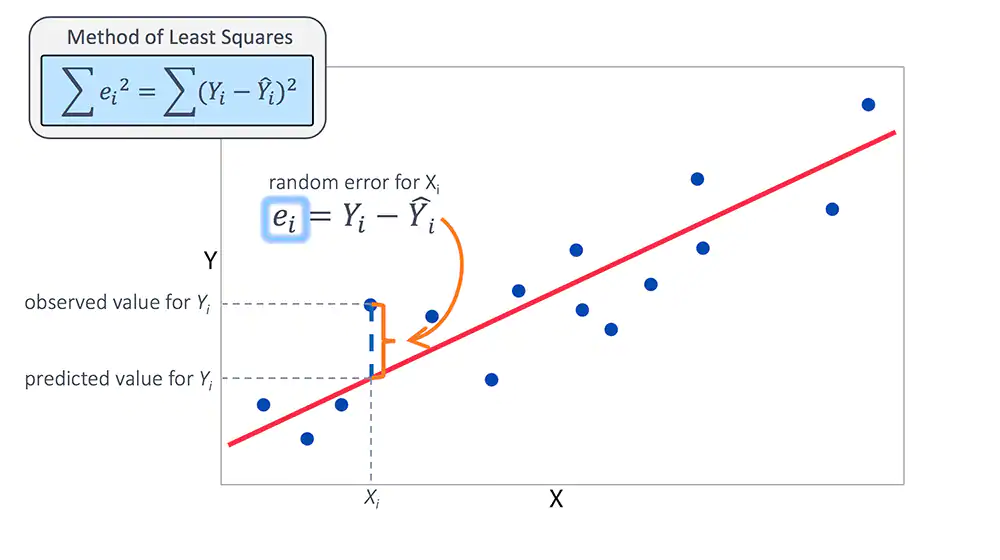
위 그림에서 분류라면 직선이 경계면이 되고, 데이터들은 그 경계면을 중심으로 분류가 되는 것이지만, 회귀는 직선이 데이터의 분포를 대표하고 포괄하는 것이다.

먼저 통계학적인 관점 에서 회귀분석을 살펴보자.

1. 통계학, 선형대수학적 관점

선형대수, 통계학적인 관점에서 단순선형 회귀분석 모델 식은 다음과 같이 linear combination과 distribution을 통해 수립할 수 있다. 에러의 기댓값(평균) $E$ 는 0이고 분산이 표준편차 $\sigma$ 의 제곱인 정규분포(가우시안 분포)를 따른다.

$\begin{bmatrix} {y_1} \\ {y_2} \\ ... \\ {y_n} \end{bmatrix}=\begin{bmatrix} 1 & x_{ 11 } & ... & { x }_{ 1k } \\ 1 & { x }_{ 21 } & ... & { x }_{ 2k } \\ ... & ... & & ... \\ 1 & { x }_{ n1 } & ... & { x }_{ nk } \end{bmatrix}\begin{bmatrix} {\beta_0} \\ {\beta_1} \\ ... \\ {\beta_k} \end{bmatrix} +\begin{bmatrix} {\varepsilon_1} \\ { \varepsilon_2} \\ ... \\ {\varepsilon_n } \end{bmatrix}$

\overrightarrow{y} = X\overrightarrow{ \beta} +\overrightarrow{\varepsilon}, \quad \overrightarrow {\varepsilon} \sim N(E(\overrightarrow{\varepsilon}) ,V(\overrightarrow {\varepsilon} ))

E(\overrightarrow {\varepsilon}) = \begin{bmatrix} 0 \\ 0 \\ ... \\ 0 \end{bmatrix}, \quad V(\overrightarrow{ \varepsilon})={\sigma^2}I

여기서 우리는 $\overrightarrow{ \beta}$ ( $\hat{\beta}$ )를 바로 구할 수도 있는데, 실제값과 모델 예측값의 차이인 오차제곱합(error sum of squares)을 최소화하면 된다. 이렇게 오차제곱합을 최소화하는 것은 최소자승법 또는 최소제곱법(Least Squared Method) 으로 이어진다.

최소제곱법(최소자승법)

통계학에서 선형 회귀 그래프를 그릴 때 보통 산점도(scatter plot)를 많이 사용한다. 그 이유는 산점도를 통해 독립변수와 종속변수간에 상관관계를 효과적으로 나타낼 수 있기 때문인데, 이 때 사용되는 척도가 $r$ 로 표기되는 상관 계수(correlation coefficient)이다.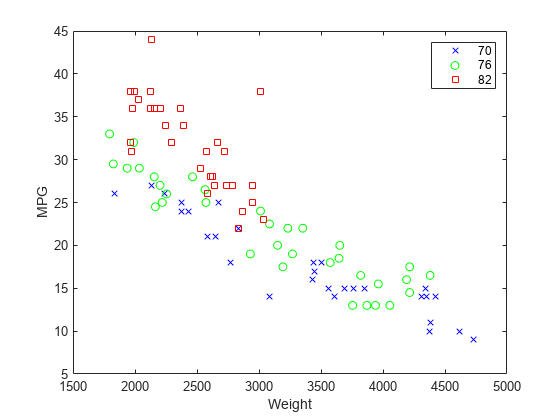

IMG Source from MathWorks

상관 계수 개념 중 가장 널리 사용되는 피어슨 상관 계수의 값에 따라 양/음의 상관 관계를 해석하고 나타낼 수 있는데, 상관관계를 떠나 좌표평면 상에 데이터가 주어지고 이 데이터가 나타내는 해가 있다고 할 때 우리말로 최소제곱법, 또는 최소자승법이라고 하는 Least Square Method/Ordinary Least Squares는 좌표 평면 상의 실제 해와 상관관계를 통해 근사한 근사 해 간의 차이를 제곱한 값들의 합이 최소가 되도록 하는 방법으로 가장 보편적으로 사용되는 회귀계수 추정법이다. 실제값과 예측(근사)값의 차이는 다른 말로 잔차(residual)이라고도 한다. 최소제곱법은 이 잔차를 최소화 하는 것이며, 직선과 데이터의 차이에서 생기는 부호를 신경쓰지 않고 최소화 하기 위해 제곱을 사용한다.

IMG Source from DSBA, Korea Univ.
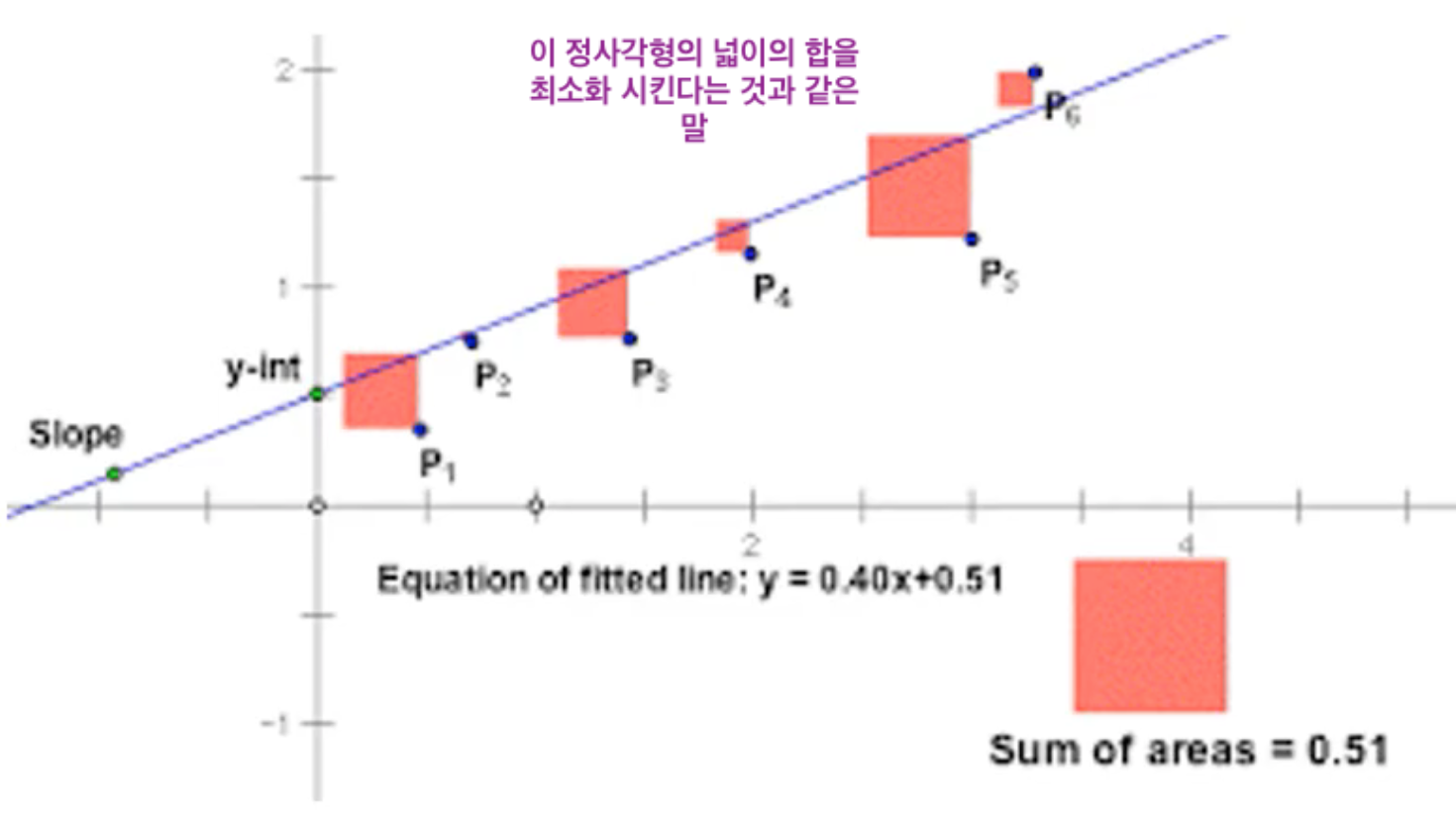
위 그래프의 설명이 잔차와 최소제곱법을 효과적으로 대변할 수 있겠다. 즉, 바꾸어 말하자면 그래프에서 표현되는 정사각형 넓이의 합을 최소화하는 것이다. 이 최소제곱법이 가능하기 위해서는 몇가지 조건이 충족 되어야 하는데,

1. 노이즈 에러(오차) $\epsilon$ 가 $\mu=0 , V= 일정$ 한 정규분포를 따라야 함
1. 독립변수와 종속변수간 linear relationship이 성립
1. 각각의 케이스들이 서로 독립이어야 함
1. 주어진 예측변수들의 집합에 대한 $Y$ 변수들의 변동성은 예측변수들의 값에 영향을 받지 말아야 함

이 네 가지가 만족이 되어야 선형방정식은 닫힌 해를 갖게 되어 최소제곱법으로 방정식을 풀 수 있게 된다. 머신러닝을 수행할 때는 두번째와 세번째 조건을 strict하게 보지 않고 관대하게 접근하는 경향이 있다. 만약 데이터들이 이 가정을 충족하지 못하면 미충족 가정에 따라 다른 방법을 사용해야 한다.Danbi_ncsoft blog, 2018

아까의 식에서 이를 만족하는 최적의 계수(coefficent) $\hat{\beta}$ 는 회귀계수에 대해 미분한 식을 0으로 놓고 풀면 transpose matrix과 inverse equation을 이용해서 다음과 같은 explicit한 해를 구할 수 있다.

\hat{ \beta } ={ \left( { X }^{ T }X \right) }^{ -1 }{ X }^{ T }\overrightarrow { y }

이렇게 회귀계수 $\hat{\beta}$ 를 추정했다면, 이 추정된 회귀계수가 얼마나 적합한지는 적합도검정(Goodness of fit)을 통해 측정할 수 있다.

IMG Source from DSBA, Korea Univ.

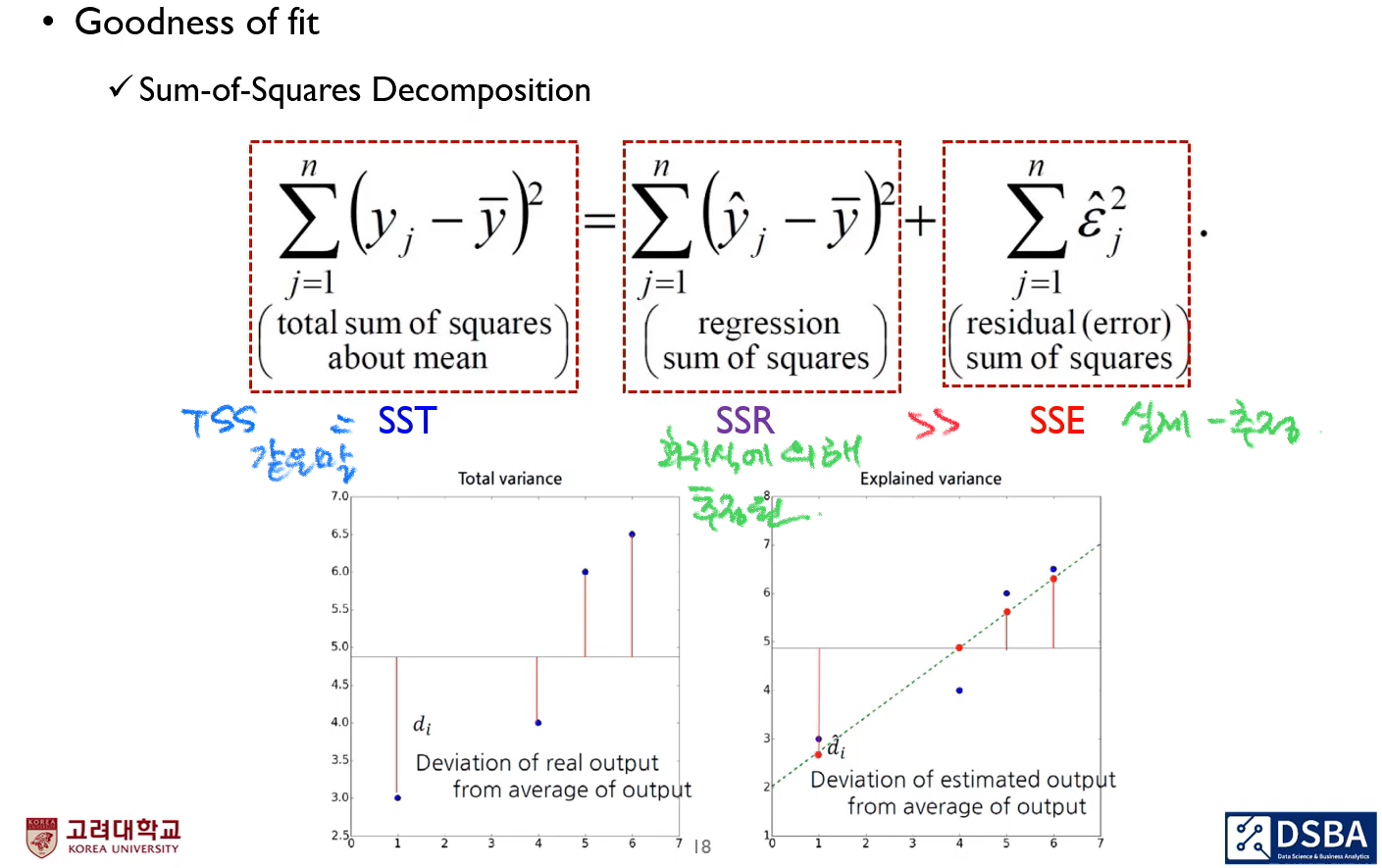
적합도 검정은 관측값들이 어떤 이론적인 분포를 따르고 있는지를 검정하는 범주형(categorical) 자료 분석법이며, 실제 관측 도수와 기대도수의 차이를 카이제곱( $\chi^2$ ) 검정 통계량으로 평가한다. 이 적합도 검정이 회귀분석에서는 Sum of Squared Decomposition을 이용해 ${SSR \over SST} = 1 - {SSE \over SST} = R^2$ 로 사용된다. $R^2$ 는 R-squared 라고 읽으며, 결정계수(coefficient of determination)이라고 한다. 종속변수의 변동량 중에서 선형회귀 모델로 설명 가능한 부분의 비율을 가리키며, $R^2$ 의 특징으로는 분산 기반으로 예측 성능을 평가하며 $0 \leq R^2 \leq 1$ 의 값을 갖는 다는 것이다. $R^2$ 가 1일 때 모든 데이터에 적합하여 완벽한 선형관계를 갖는 것을 뜻하고, 0이면 예측변수와 목적변수(설명변수와 종속변수) 간에 선형관계가 없다는 것이다. .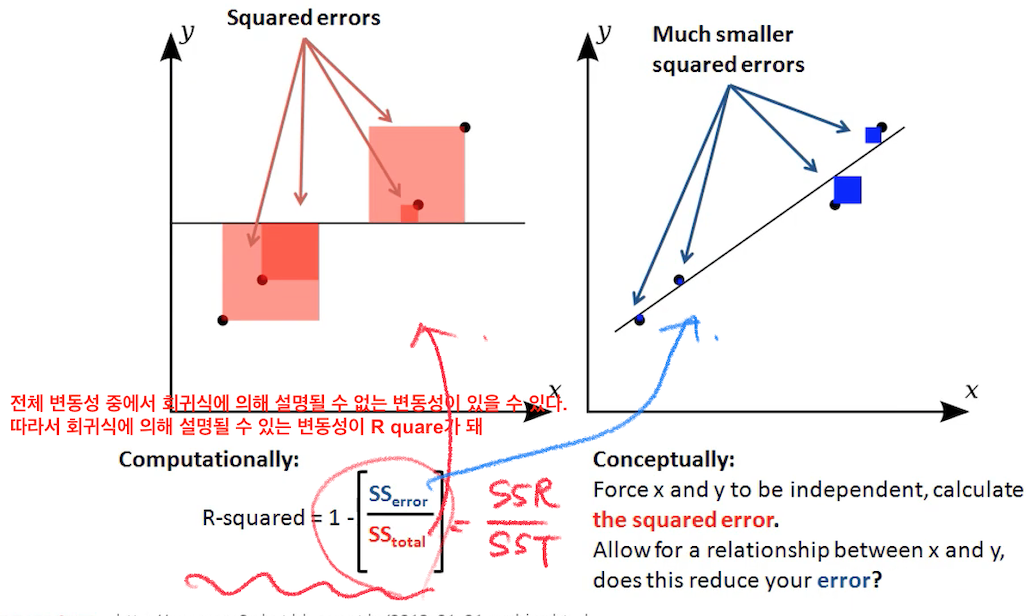

IMG Source from compare2what
그러나

R^2

는 선형관계 여부에 관계없이 설명변수의 개수가 많으면 증가 하기 때문에 분석에 유의미한 영향을 줄 수 있다고 오인할 수 있다는 것이 단점이다. 이 단점을 보완한 수정

R^2

이 있으며, 영어로는 adjusted

R^2

라고 한다.

IMG Source from DSBA, Korea Univ.

2. 기계학습적 관점

사실 기계학습적 관점이라고 해도 수학적 관점과 맞닿아있기 때문에 나누는게 의미도 없고, 엄청 정확하지도 않다. 그럼에도 나눈 이유는, 머신러닝을 하면서 선형 회귀는 최소제곱법, 최대우도/가능도를 이용하여 접근 하는 것이 중요하기 때문이다.

들어가기에 앞서 다음 사전 지식을 이해하고 넘어가자. 기계학습 관점에서 선형 모델을 수립할 때 입력 데이터 $\bold x$ 와 가중치 파라미터 $\bold w$ 벡터로 다음의 관계식을 표기할 수 있으며, 이를 선형 기저함수 모형(linear baseline function model)이라고 한다.

y(\bold {x,w}) = w_0 + w_{1}x_{1} + \dots + w_{D}x_{D}

입력 데이터 $\bold x$ 에 대해 비선형 함수는 non-linear baseline function을 나타내는 $\phi_j(\bold x)$ notation을 사용해서 다음과 같이 나타낸다.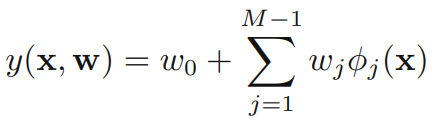

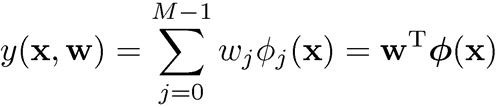
최대가능도(Maximum Likelihood Method)

지난편의 분포-2 에서 잠깐 다룬 가능도(likelihood)의 개념을 다시 복습해보자. 가능도는 '우도'라고도 하며, 어떤 모델의 모수가 될 뻔한 가능성이다. 가능도는 확률과 밀접한 연관을 가지고 있어 어떤 확률 변수 $X$ 가 모수 $\theta$ 에 대한 확률 분포 $P_\theta(X)$ 를 가지며 $X$ 가 특정한 값 x로 표본 추출 되었을 때 모수 $\theta$ 에 대한 가능도 함수는 다음과 같이 정의 되며, $\theta$ 가 전제 되었을 때 sample $x$ 가 등장할 확률에 비례한다고 하였다.

L(\theta | x) = P(X = x|\theta) \\ L(\theta; x_1, x_2, \dots, x_n) = f(x_1;\theta)f(x_2;\theta)\cdots f(x_n;\theta)

주어진 관측값 $x_1,x_2,\dots,x_n$ 에 대해 가능도함수의 곱을 최대로 한 $\theta$ 를 추정치로 정한 것이 최대가능도(최대우도)추정법이며, 선형회귀에서 에러 함수가 정규분포(가우시안 분포)를 따를 때 다음과 같은 식을 갖는다.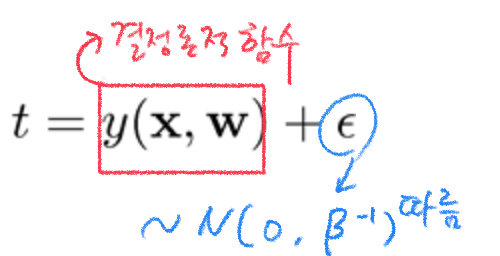

수식이 낯설게 느껴질 수 있지만 맨앞의 선형방정식과 같다고 생각하면 되며, $t$ 는 선형방정식의 $f(x)$ 라고 동일선상에 놓고 보자. 이 때 $t$ 의 분포는 다음과 같이 정리 된다.

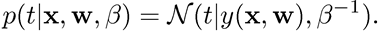
만약 제곱합이 모델의 loss function으로 사용되면, 새로운 $\bold x$ 가 주어졌을 때 $t$ 의 최적의 예측은 $t$ 의 조건부 기댓값이다. 따라서 위의 분포를 따르는 t의 조건부 기댓값 $\mathbb{E}[t|\bold x]$ 은 아래식으로 표현이 되며 이것이 결정론적 함수(deterministic function)가 된다.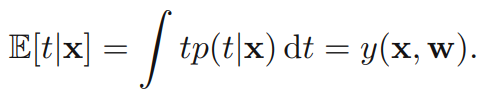

입력값이 $\bold X= \bold{x_1, ..., x_N}$ 이고 출력값 $\bold t$ 가 $\bold t= t_1, ..., t_N$ 일 때, 비선형함수에서의 파라미터인 가중치 벡터 $\bold w$ 는 어떻게 될까? 최대가능도추정법(MLE)을 사용하면 가능도함수(likelihood function, $L(\theta)$ 로 표기)와 여기에 로그를 씌운 로그 가능도함수(log-likelihood function, $l(\theta)$ 로 표기)는 다음과 같이 된다.

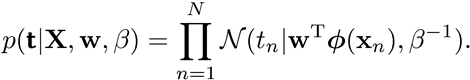
로그 가능도함수를 최대로 하기 위해서는 에러함수가 곧 최소화 되어야 한다는 것을 의미하므로, 제곱합 에러함수 $E_D(\bold x)$ 는 다음과 같고 이를 미분했을 때 0이 된다.

$w_0 = \bar{t} - \sum_{j=1}^{M-1} w_j\bar{\phi_j} ,$
$\bar{t} = {1 \over N}\sum_{n=1}^{N}t_n$
$\bar{\phi_j} = {1 \over N}\sum_{n=1}^{N}\phi_j(\bold x_n)$

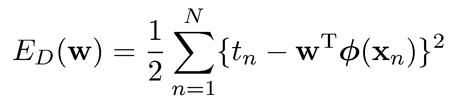
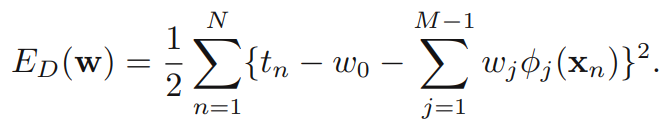
MLE는 관측된 표본(sample)에 근거하여 관측 불가능한 parameter와 표본들로부터 알려지지 않은 모집단 확률분포의 형태를 추정하는 방법 중 하나이다. 관심이 있는 확률변수나 파라미터에 대해 사전 정보를 요하지 않는 통계 추정법으로 적합하며, 구체적으로 모집단의 특성을 모르는 경우 사용한다. 머신러닝에서는 주로 모집단의 특정을 단번에 파악할 수는 없을 때 주어진 데이터인 표본으로 모집단을 나타내는 수치인 모수(parameter)와 확률변수 등의 점추정치를 알기 위해 널리 사용되고 있다. 표본 수가 충분히 클 때 효과적인 통계적 속성을 지닌다는 장점을 지니고 있다.

회귀-1편을 마치며...

머신러닝이 수학과 깊은 연관이 있다는 것을 알고는 있었지만 자료를 찾아보고 정리할 수록 이렇게 깊은 배경이 있나 하는 것을 많이 느낄 수 있었다. 최소제곱법과 최대우도법만 해도 분량이 제법 되어 우선은 1편에서는 여기까지만 다루도록하고 2편에서는 편향-분산 등가교환과 정규화에 대해 알아보자.