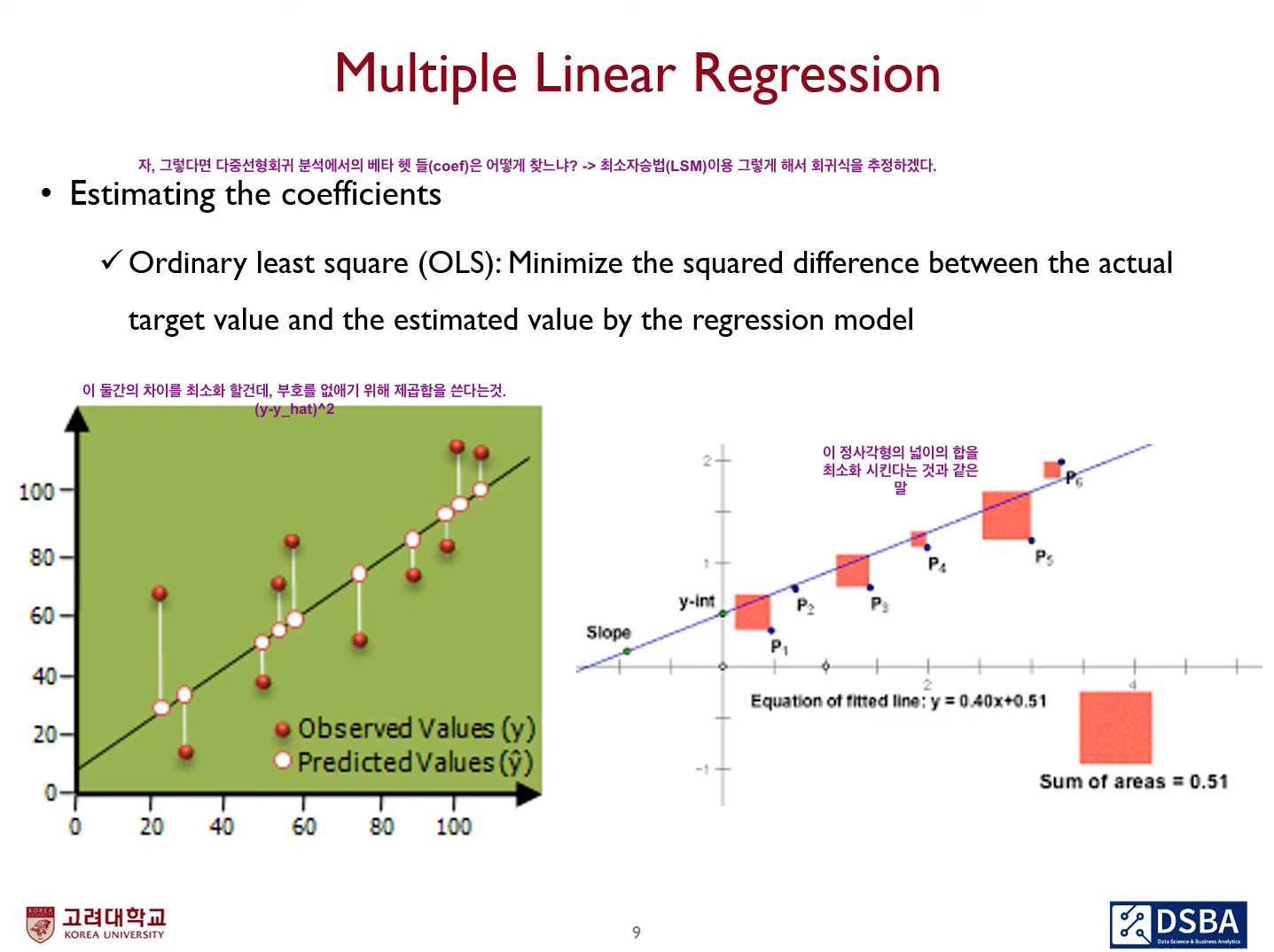
(Review) Linear Regression

이 포스트는 이전 포스트인 4편 회귀-1.최대가능도,최소제곱법과 연관이 깊은 주제이기 때문에 회귀에 대한 전반적인 개념이 없다면 위 링크를 클릭해서 참고해주시기 바랍니다.

선형 회귀 개념을 하나의 포스트로 압축하기에는 그 양과 중요성이 너무 크기 때문에 지난 포스트에서는 선형회귀의 개념과 수식, 그리고 회귀계수와 식을 도출하고 검정하는 것을 최대가능도와 최소제곱법을 통해 알아보았다면, 이번 회귀 2편에서는 회귀와 머신러닝에서 빼놓을 수 없는 모델 피팅(model fitting)에 깊이 연관된 선형방정식의 error term과 fitting의 종류, 그리고 정규화 테크닉 에 대해 다뤄볼 것이다.

먼저 회귀분석, 그중 선형 회귀(Linear regression)에 대해 간단히 복습을 하자면, 한개 이상의 수치형 설명변수 X와 연속형 종속변수 Y간에 선형관계가 성립한다고 할 때 이 관계를 가장 잘 표현할 수 있는 회귀계수를 선형방정식으로 나타내는 것을 의미하며, 실제값과 추정값의 차이의 제곱을 최소화하는 하는 것을 목표로 한다.

머신러닝 관점에서 이제 접근하면, 이렇게 수립한 regression model이 주어진 데이터셋에 대해 training을 거친 후, test data셋에 대해서도 얼마나 잘 학습하냐 하는 걸 따지고 검토할 필요가 있다. 이 때 고려해야 할 것이 영어로 "Regressing Y on(to) X"라고 하는 선형식

에서 오차항을 나타내는 $\epsilon$이다. 이 오차는 영어로 error라고 하며, error는 bias와 variance 이렇게 두 종류로 나뉜다.

Bias-Variance Trade-off

한국말로 편향-분산 딜레마라고도 하는 이 트레이드 오프(등가교환)는 지도학습(supervisded learning)에서 학습이 trainset위주로 지나지체 일반화 하는 것을 막기 위해 error를 최소화 할 때 겪는 문제이다.[Wikipedia, searched in 2021] 일반화는 영어로 generalization이며, 모델이 한번도 경험하지 못했던 데이터에 대해 얼마나 잘 학습하냐 하는 것을 의미한다. 이 일반화의 정도에 따라 모델학습에 있어 다음과 같은 문제가 발생할 수 있다.

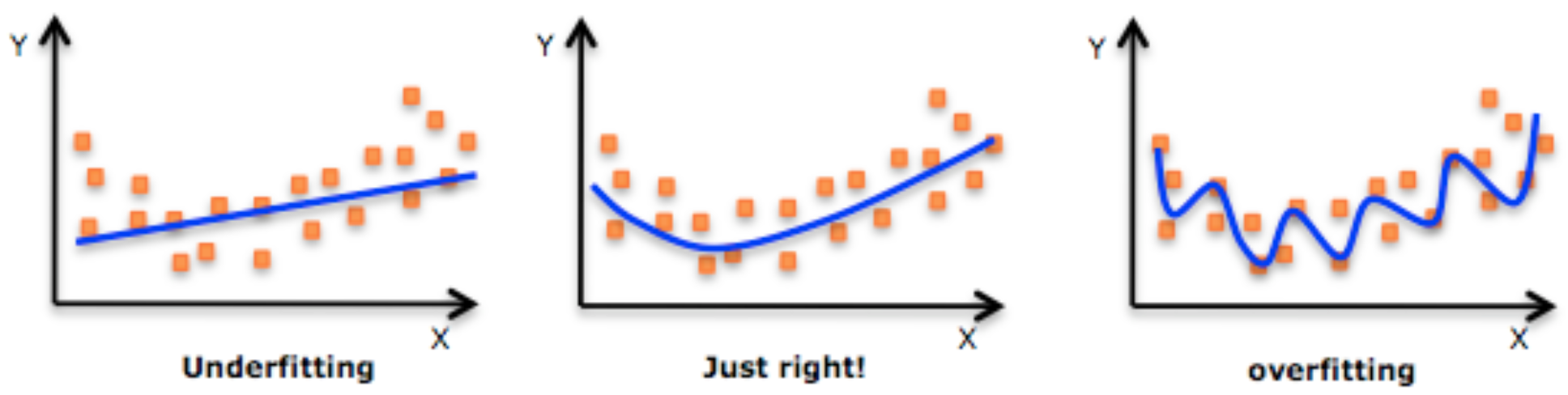
이렇게 묘사된 일반화의 정도를 이해하는 것은 머신러닝을 함에 있어 매우 중요한 과정이다. 이 일반화에 영향을 미치는 것이 오차(에러)이며, 오차는 모델링을 할수도, 할 필요도 없다.

오차의 두 종류 중 편향(bias) 은 알고리즘 가정에서 잘못 설정하는 등(예를 들어 비선형인데 선형으로 접근)의 오류가 있어 학습을 했을 때 발생하는 오차이다. 상수로 주어진, 변화될 가능성이 없는 값이며 편향이 높을 수록 모델이 단순하여 데이터의 특징과 결과 변수가 가지는 관계를 놓치는 underfitting 문제를 야기하며, 학습이 제대로 이루어지지 않았음을 시사한다. 한편, 분산과 달리 학습데이터가 적든 많든 일정한 수준의 error로 수렴하기 때문에 편향을 개선하기 위해서는 다른 관점으로 모델을 구상해야함.

분산(variance) 은 trainset에 있는 작은 변동성(fluctuation) 때문에 발생하는 오차이며, 보통 모델이 복잡함에도, 높을 수록 노이즈까지 모델링에 포함시켜 덜 정확한 추정을 하는 overfitting 문제를 일으킨다. 보통 학습데이터를 많이 확보하면 도움이 된다.

이 둘을 완전히 충족하는 알고리즘을 모델링하는 것은 사실상 불가능한데, 두 종류의 오차들이 가지는 관계는 다음과 같다.

IMG Source from scott.fortmann-roe.com

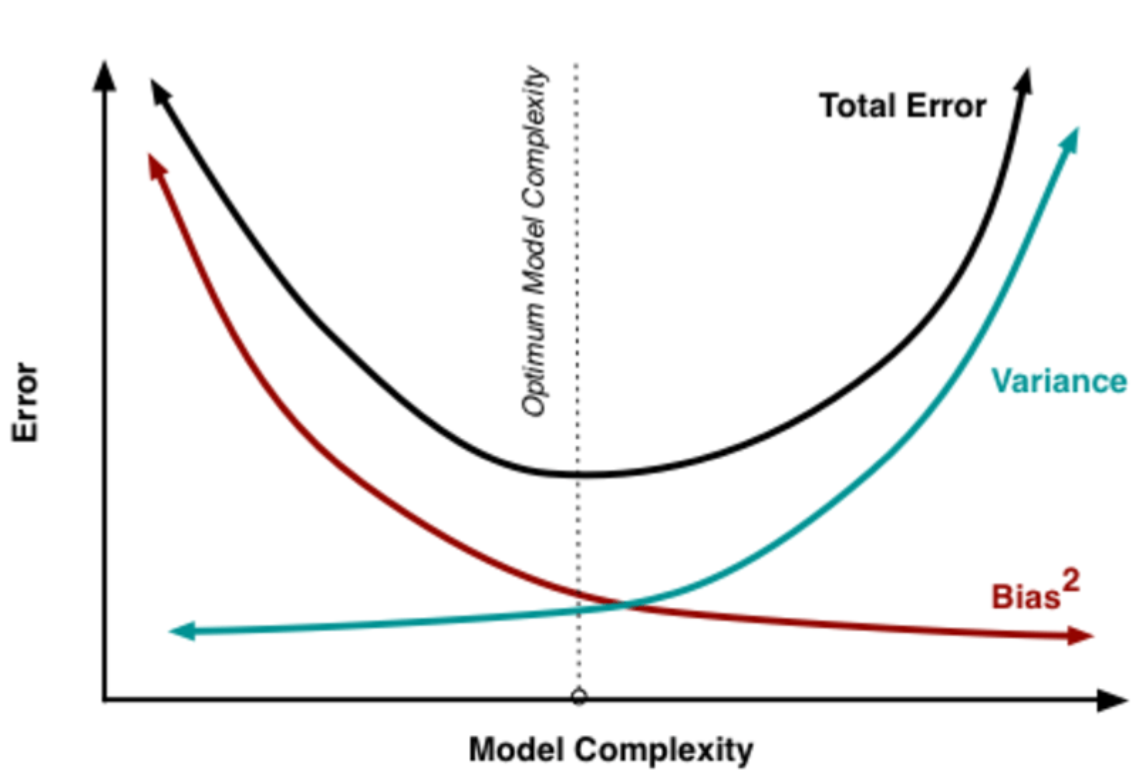
이만큼 둘 간의 관계를 적절히 나타낸 그래프가 없을만큼 총 에러(노이즈)에서 편향과 분산이 어떤 관계를 가지는 지 잘 담아내고 있다. 가운데에 분산과 편향(정확히는 편향의 제곱)이 서로 교차(만나)하는 지점이 에러를 최소화하는 지점이며, $Y = f(X) + \epsilon$에서 노이즈 $\epsilon$가 평균이 0이고 분산이 $\sigma^2$인 정규분포를 따를 때 $(x_1,y_1), \dots, (x_n, y_n)$ 데이터가 있고 함수적인 관계를 가질 때 실제값과 추정치 사이의 평균 제곱 오차($E(\hat{Y} - Y = \epsilon))$는 다음 과정을 거쳐 도출할 수 있다. 참고로 이 평균 제곱 오차는 영어로 Mean Square Error이며 줄여서 MSE로 표기를 한다.

Bias-Variance Decomposition(분해)

위키피디아의 편향-분산 변환 과정에 따르면, $f = f(x)$라 하고, 추정치인 $\hat{f} = \hat{f}(x)$라 하면, 확률 변수 $X$에 대해

가 성립하여 $\mathrm {Var}[X] = \mathrm {E} [X^{2}] - \mathrm {E}[X]^{2}$ 관계를 가짐을 알 수 있고, $f$의 값들은 결정되어 있으므로

${\begin{aligned}0=\mathrm {Var} [f]=\mathrm {E} [(f-\mathrm {E} [f])^{2}]\Rightarrow f-\mathrm {E} [f]=0 &\\ \Rightarrow \mathrm {E} [f] = \mathrm {E} [f+\epsilon ]=f = \mathrm {E} [y]\end{aligned}}$

가 성립한다. 그리고 에러가 분산이 $\sigma^2$인 정규 분포를 따른다고 하여 $\mathrm {Var}[\epsilon] = \sigma^2$ 이므로,

${\begin{aligned}\mathrm {Var} [y]=\mathrm {E} [(y-\mathrm {E} [y])^{2}]=\mathrm {E} [(y-f)^{2}]=\mathrm {E} [(f+\epsilon -f)^{2}]=\mathrm {E} [\epsilon ^{2}]=\mathrm {Var} [\epsilon ]+\mathrm {E} [\epsilon ]^{2}=\sigma ^{2}\end{aligned}}$

이 때 $\epsilon와 \hat f$는 서로 독립이므로 기댓값의 특성에 따라 연산은 다음과 같이 분해가 가능하다.

• 편향: ${\begin{aligned}\mathrm {Bias} {\big [}{\hat {f}}(x){\big ]}=\mathrm {E} {\big [}{\hat {f}}(x)-f(x){\big ]}\end{aligned}}$
• 분산: ${\begin{aligned}\mathrm {Var} {\big [}{\hat {f}}(x) = \hat{f}{\big ]}=\mathrm {E} {\Big [}{\big (}{\hat {f}}(x)-\mathrm {E} [{\hat {f}}(x)]{\big )}^{2}{\Big ]}\end{aligned}}$
• 여기서 $\sigma^2$은 줄일 수 없는 오차로, 모든 항의 값이 0 이상이므로 보이지 않는 표본들의 기대 오차의 하한값 역할을 함
• ${\hat {f}}(x)$가 복잡할 수록 더 많은 데이터들을 캐치할 수 있어 편향은 작아지나, 캐치하기 위해 더 많이 이동해야 하므로 분산은 커지게 됨

그렇다면 이제 편향과 분산의 영향과 관계를 알았는데, 이것들을 어떻게 줄여서 일반화의 성능을 높일 수 있을까? 이를 위한 테크닉이 여러가지가 있는데, 분산을 줄임으로 모델의 과적합을 방지하는 기법이 바로 정규화 또는 규칙화 라고 부르는 regularization techniques 이다.

Regularized Regression

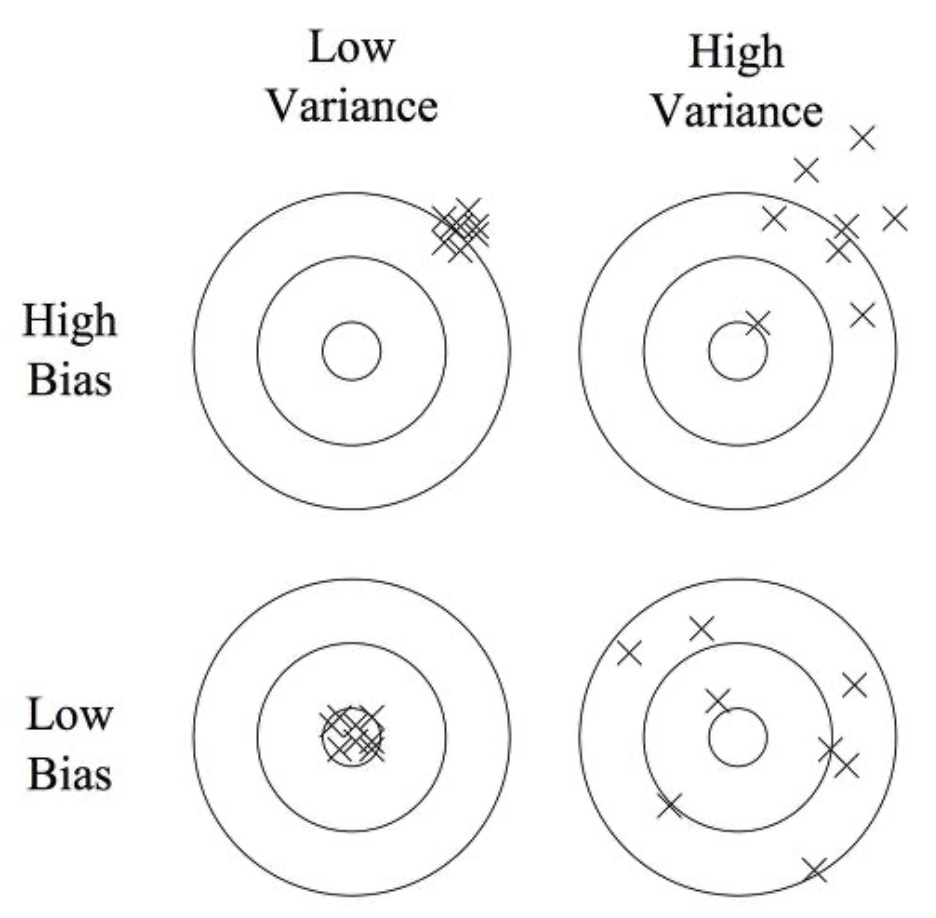
위 그림에서 편향과 분산 둘다 줄인 세 번째 알고리즘을 구현한 모델이 가장 이상적이겠지만, 그렇게 하는 건 거의 불가능에 가깝다고 하였다. 이에 분산을 줄이거나, 편향을 줄이는 등으로 에러를 최소화 하며 근사 성능을 높이는데, linear regression에서 분산을 줄임으로 일반화 성능을 끌어 올릴 수 있으며(이 과정에서 편향이 오를 수는 있다), 이것이 적용된 회귀를 바로 regularized linear regression이라고 한다.

먼저 정규화(Regularization)의 기본 원리는 회귀 계수로 표현되는 $\beta$에 제약 조건을 부여하는 방법이다. 최소제곱법을 통해 평균제곱오차를 최소화하는 회귀계수들을 구한 뒤 어떤 제약 조건을 넣느냐에 따라 3가지 regularization 형태가 있으며, Rige Regression(릿지), Lasso Regression(라쏘), 그리고 elasticnet regression(엘라스틱넷)이 그것이다.

들어가기에 앞서 제약조건과 연관하여 짚고 넘어가야 할 수학개념이 있는데 norm(노름) 이라는 것을 알고 가자. 선형대수학의 관점에서 원소들에 일종의 '길이'나 '크기'를 부여한 벡터공간을 normed space라고 한다. 그 벡터원소가 가지는 크기를 측정하는 함수를 norm이라 하며, 삼각 부등식을 따라 거리 함수를 정의하고 절대값 기호 ||를 붙여 $\left\lVert \dots \right\rVert$ 나타낸다. Norm이 측정한 벡터의 크기는 원점에서 벡터 좌표까지 거리 혹은 Magnitude라고 한다. 정의된 함수는 다음과 같다.

여기서 $p$는 Norm의 차수(dimension)을 나타내는데 $p=1$이면 이것을 L1 Norm이라고 부르고 $p=2$이면 L2 Norm이라고 부른다. $n$은 벡터의 feature 수이다. 따라서 거리함수 $L_p$는 feature 절대값을 $p$번 곱한 값의 합을 $p$번 제곱근한 값이다. [Taewan K.(Dec 15, 2017)]

1. Ridge Regression

자 위에서 Norm 개념에 대해 언급을 했다. 그리고 이 포스트를 시작하면서 최소제곱법의 연장선이라고 하였는데 최소제곱법(Least Squared Method)의 해인 $\hat{\beta}$는 $\hat { y } =X \beta$식에서 아래와 같이 편미분식을 0으로 놓고 풀면 다음과 같이 명시적으로 구할 수 있다고 하였다.

ridge regression, 우리말로 릿지 회귀라고 하는 것은 평균제곱오차(MSE)를 최소화하면서 error 중 bias를 소폭 허용하여 variance를 줄이기 위해 회귀계수 벡터 $\beta$의 L2 norm을 제한하는 기법이다.

이를 최소제곱법 수식과 함께 쓰면 다음과 같다. 여기서 $\lambda$는 제약을 얼마나 강하게 걸지 결정해주는 값으로 사용자가 지정하는 하이퍼파라미터이다.

릿지회귀의 해인 회귀계수 벡터 $β$는 위 식을 $β$로 미분한 식을 0으로 놓고 풀면 다음과 같이 명시적으로 구할 수 있다.

$\lambda I$가 더 붙은 것을 알 수 있으며, 이 역시 최소화 하는 것이 ridge regression의 궁극적인 목표이다.

Ridge regression은 선형회귀에 $L_2$ 정규화가 더해진 것으로도 해석할 수 있는데, $L_2 nor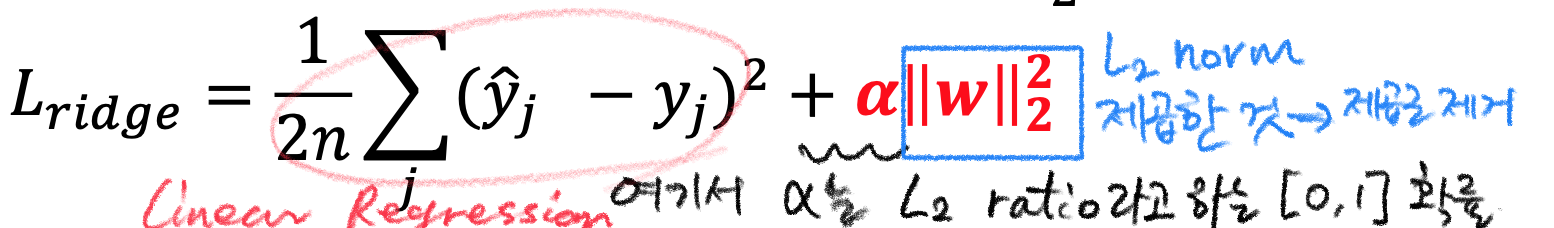m \left\lVert w \right\rVert_2 = \sqrt{\sum_{i}^n {w_i^2}} = \sqrt{w_1^2+w_2^2 + \dots+w_n^2}$로 정리하면
이렇게 된다. 왼쪽에 1/2n은 미분을 위한 트릭이라고 생각하면 되며, 전형적인 선형방정식에 L2 norm과 $\alpha$ 계수가 들어갔다. 이는 L2 ratio라고 하며, 머신러닝 툴에서 조작가능한 하이퍼 파라미터로 취급되어 이를 조절하는 정도에 따라 ridge 영향이 달라지는데, L2 정규화가 도입된 ridge 정규화는 아래와 같이 큰 weight을 가진 변수의 영향을 줄이는 역할을 한다.

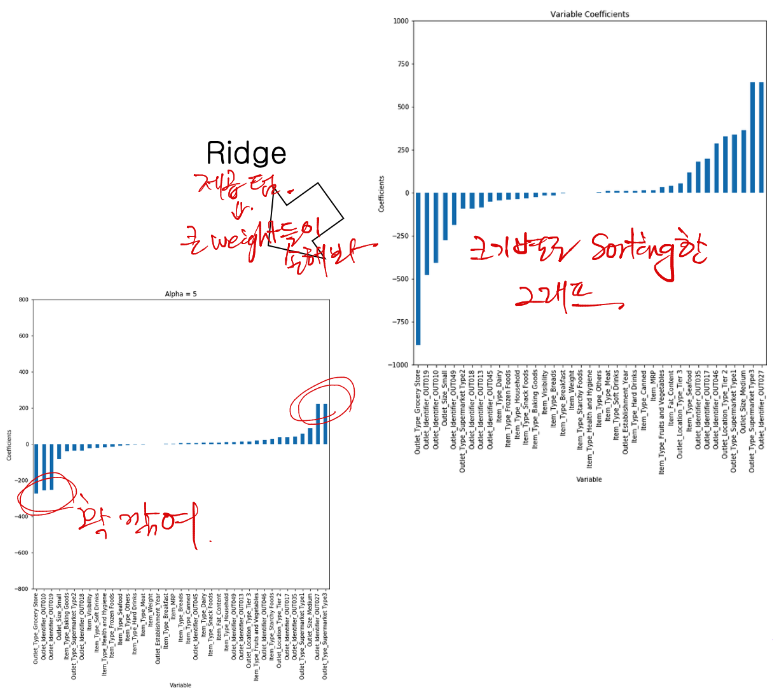
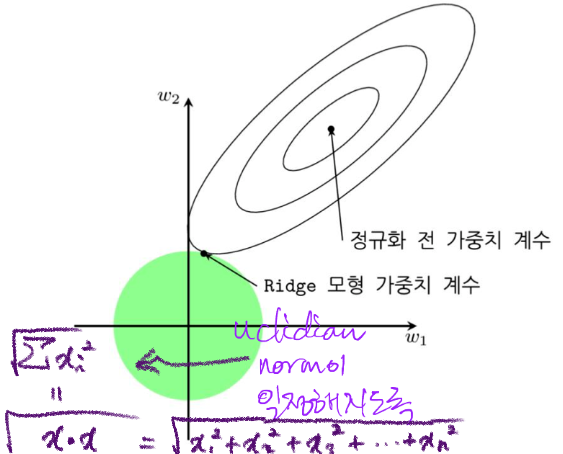
기하 해석까지 넓히면 다음과 같으며, 정규화 전 가중치 계수는 릿지 적용후 타원모양의 자취를 그리며, 접점이 MSE가 최소인 지점이다. 원의 반지름이 작아질 수록 $L2$ norm이 감소하며 이는 그만큼 제약이 커진다고 이해할 수 있다. 바꿔말하면 하이퍼 파라미터 $λ$가 클수록 $β$의 $𝐿2$ norm이 줄어든다.

2. LASSO Regression

라쏘(LASSO:Least Absolute Shrinkage and Selection Operator) 회귀는 릿지와 비슷한 형태를 가지나, L1 norm을 제약한다는 것이 차이점이다. 목적식과 제약식을 포괄하는 라쏘 회귀계수는 다음과 같다.

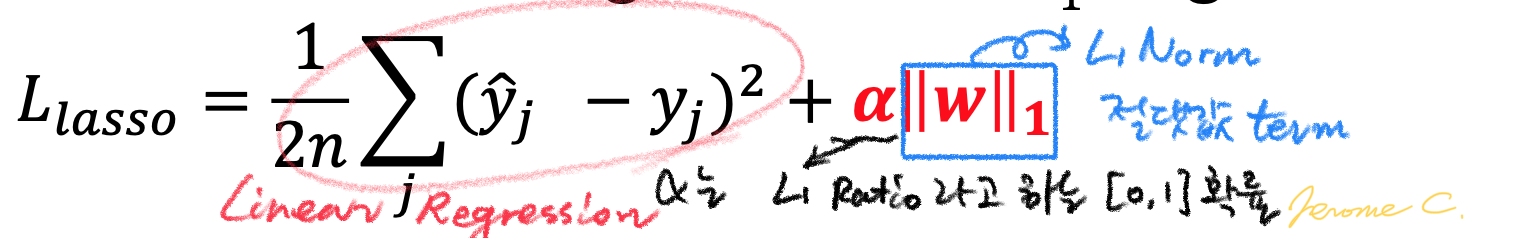
Taxicab norm 또는 Manhatten norm이라고 하는 L1 norm은 벡터의 요소에 대한 절댓값의 합으로 표현되는데, L2 norm과 달리 미분이 불가능하기 때문에 라쏘회귀의 해를 단번에 구할 수 없다는 단점이 있지만(물론 구하는 방법이 없는 건 아님) 요소의 값 변화를 정확하게 파악하는 특징도 지니고 있다. LASSO 회귀의 특성을 기하학적으로 나타내면 다음과 같다.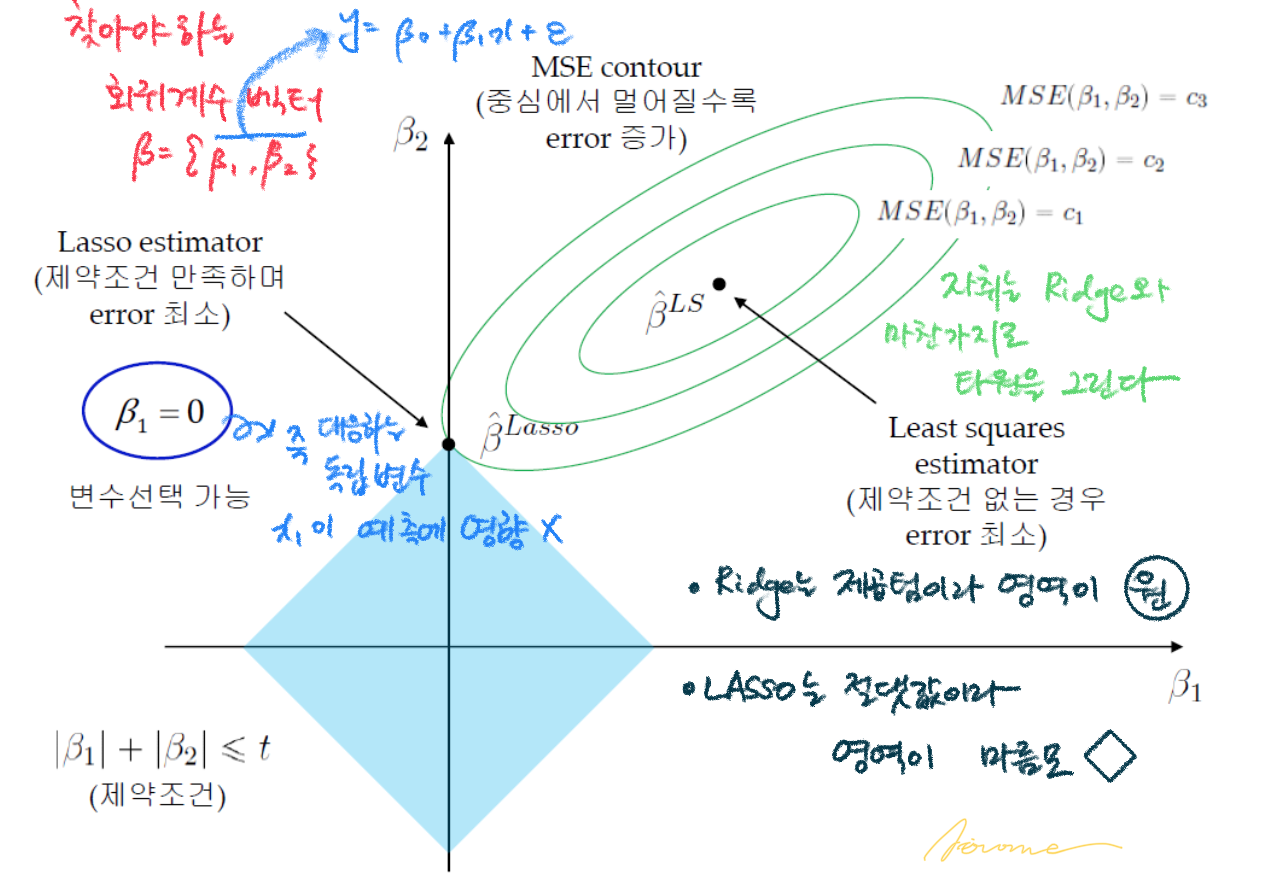

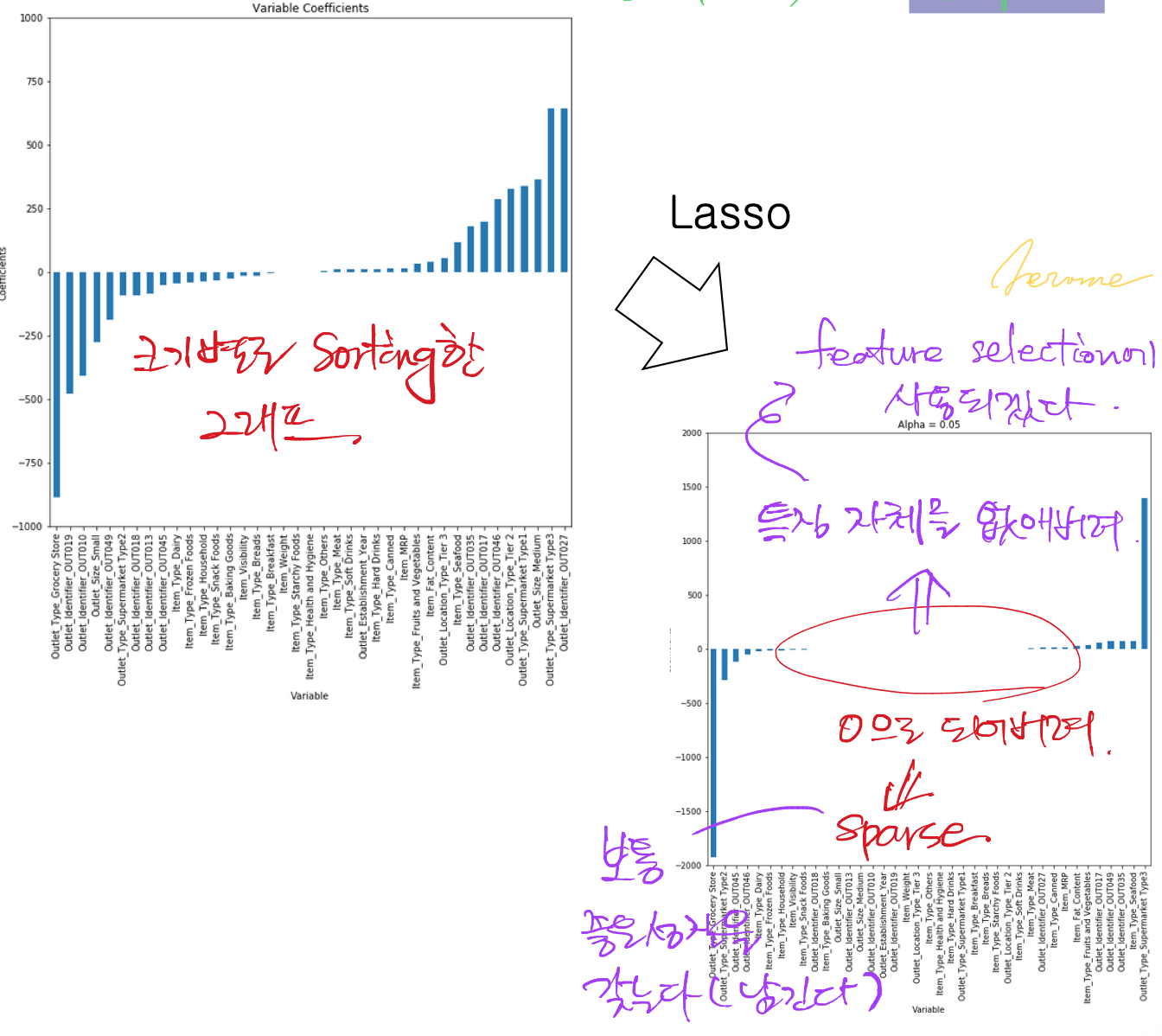
IMG Source from imgur.com

이렇게 L1 norm이 적용된 LASSO 회귀는 예측에 중요하지 않은 변수의 회귀계수/가중치를 감소시키는 변수선택 역할을 한다.

3. Elasticnet Regression

LASSO와 Ridge 회귀 저마다 변수에 제약을 가하는 특성이 L1 / L2 norm 선택에 따라 다르다는 것은 확인했는데, 이 둘의 특징을 회귀에서 함께 갖고 싶을 수도 있다. 이를 충족하기 위한 정규화 테크닉은 엘라스틱넷(elasticnet) 회귀이며, 제약식에 L1, L2 norm을 모두 쓰는 것이다.

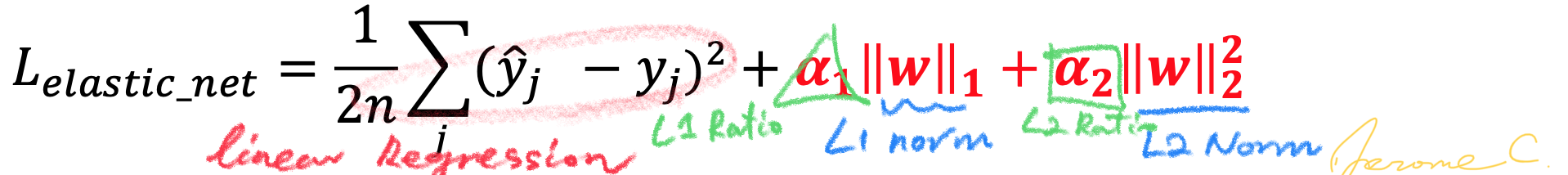
위 식에서 보듯 L1 ratio, L2 ratio 두가지가 들어가는데, $\alpha$를 하나로 통일하기 위해 $\alpha_1 = \alpha, \alpha_2 = (1-\alpha)$ 이렇게 확률의 성질과 결합해서 나타내기도 한다.

이 세가지 정규화 테크닉을 표로 정리하면 다음과 같다.

IMG Source from ratsgo's blog

4. Using these in scikit-learn Python module

파이썬의 사이킷런에서는 앞서 배운 선형분류부터 선형회귀, 그리고 정규화 기법들이 채택된 모델을 간편하게 제공해주고 있다. 코드는 다음과 같이 간단하여 import해야할 패키지만 안다면 손쉽게 실습해볼 수 있다.

# 이미 데이터가 있고, trainset과 testset으로 적절히 스플릿되어 있다는 가정 하에

# Linear Regression
from sklearn.linear_model import LinearRegression
linreg = LinearRegression().fit(X_tr, y_tr)
y_hat = linreg.predict(X_ts)

# Ridge Regression
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1e1).fit(X_tr, y_tr) 	# default alpha = 1
y_hat = ridge.predict(X_ts)

# LASSO Regression
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1e2).fit(X_tr, y_tr) # default alpha = 1
y_hat = lasso.predict(X_ts)

# ElasticNet Regression
from sklearn.linear_model import ElasticNet
enet = ElasticNet(alpha=1e3, l1_ratio=0.3).fit(X_tr, y_tr) # # default alpha = 1, l1_ratio = 0.5
y_hat = enet.predict(X_ts)

# Linear Classification
# SGDClassifier, RidgeClassifier 등으로 제공
# ex)
from sklearn.linear_model import SGDClassifier
sgd = SGDClassifier().fit(X_tr, y_tr)
y_hat = sgd.predict(X_ts)
score = sgd.score(X_ts, y_ts) 	# for testset

회귀 2편을 마치며...

이렇게 분류 다음 회귀에 관해 두번의 포스트를 마치게 되었다. 머신러닝은 곧 수학이라는 말이 여전히 적용되는 파트임을 또한번 느낄 수 있었다. 자세한 배경과 수식, 그리고 기하학적 해석까지 더해지면 본 포스트로는 빈약하다 할만큼 방대하지만, 학부생 수준에서는 이정도만 제대로 알고 있어도 좋지 않을까 생각한다. 대신 선형대수학과 통계학 지식은 갖추고 있어야함은 물론이다.

다음편에는 regression이라는 단어가 들어가지만 그 특징이 분류에 가까운 linear task 기법인 Logistic Regression에 대해 다뤄보겠다.

References

• 보물찾기.(May 19, 2017) Bias-variance decomposition. Github blog post. Retrieved from
  https://ratsgo.github.io/machine%20learning/2017/05/19/biasvar/
• 보물찾기.(May 22, 2017) Regularized linear regression. Github blog post. Retrieved from
  https://ratsgo.github.io/machine%20learning/2017/05/22/RLR/
• Go's blog.(Jan 20, 2018) [ISL] 3장 - 선형회귀 이해하기. Github blog post. Retrieved from
  https://godongyoung.github.io/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D/2018/01/20/ISL-linear-regression_ch3.html
• Taewan K.(Dec 15, 2017) 딥러닝을 위한 Norm, 노름. own blog post. Retrieved from
  http://taewan.kim/post/norm/
• Sangwon P.(Aug 5, 2017) Coursera Machine Learning(by Andrew Ng)_강의 정리. Retrieved from
  https://www.slideshare.net/freepsw/coursera-machine-learning-by-andrew-ng
• Injung K. (2020) 03. Linearmodels lecture slides. Deeplearning application subject in fall semester. HGU, South Korea