
2021-02-10
큐, 스택, 링크드리스트등 다양한 자료구조를 SSAFY수업을 통해 학습하게 되었고 수업을 바탕으로한 탐색 알고리즘을 공부하였습니다. 다익스트라 알고리즘과 플로이드 와샬 알고리즘을 조금 더 쉽게 이해하기 위해서 DP를 먼저 선행해서 학습하였습니다. 그리고 스터디를 통해서 알게된 새로운 지식은 최소신장 트리를 사용할 때 분할속성과 사이클을 확인하기 위해서 크루스칼알고리즘과 유니온파인드와로 최소신장트리가 가능한지 확인 할 수 있다라는것을 추가적으로 알게 되었습니다.
탐색 알고리즘
BFS(Breath First Search)
너비 우선 탐색은 탐색을 할 때 너비를 우선으로 하여 탐색을 수행하는 탐색 알고리즘 입니다. 특히나 "맹목적인 탐색"을 하고자 할 때 사용할 수 있는 탐색 기법 입니다. 너비 우선 탐색은 최단 경로를 찾아준다는 점에서 최단 길이를 보장해야 할 때 많이 사용한다.
-
핵심 아이디어
루트 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방법
→ 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회방법
-
BFS가 필요한 경우
두 노드 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택한다
Ex) 지구상에 존재하는 모든 친구 관계를 그래프로 표현한 후 알고자 하는 친구 사이에 존재하는 경로를 찾는 경우
깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야 할지도 모른다.
너비 우선 탐색의 경우 - 찾고자 하는 친구와 가까운 관계부터 탐색 -
너비 우선 탐색(BFS)의 특징
직관적이지 않은 면이 있다.
→BFS는 시작 노드에서 시작해서 거리에 따라 단계별로 탐색한다고 볼 수 있다.BFS는 재귀적으로 동작하지 않는다. →이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다. →이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다. BFS는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 자료 구조인 **큐(Queue)**를 사용한다. →즉, 선입선출(FIFO) 원칙으로 탐색 →일반적으로 큐를 이용해서 반복적 형태로 구현하는 것이 가장 잘 동작한다. -
시간 복잡도
너비 우선 탐색(BFS)의 시간 복잡도
인접 리스트로 표현된 그래프: O(N+E)
인접 행렬로 표현된 그래프: O(N^2)
깊이 우선 탐색(DFS)과 마찬가지로 그래프 내에 적은 숫자의 간선만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.
public void bfs() {
if(isEmpty())return;
//탐색 순서 번호를 큐로 관리
Queue<Integer> que = new LinkedList<Integer>();
que.offer(1);
int current;
while(!que.isEmpty()) {
current = que.poll();
System.out.println(nodes[current]);
if(current*2<=lastIndex) //왼쪽자식
{
que.offer(current*2);
}
if(current*2+1<=lastIndex) //왼쪽자식
{
que.offer(current*2+1);
}
}
}
//너비 정보를 따로 갖고 있지 않고 레벨에따라 구분할수 있는 bfs 탐색
public void bfs2() {
if(isEmpty())return;
Queue<Integer> que = new LinkedList<>();
que.offer(1);
int current,size,level=0;
//탐색 순서 번호를 큐로 관리
while(!que.isEmpty()) {
//레벨
//사이즈를 체크하고
size = que.size();
System.out.println("level "+ level);
//사이즈 만큼 체크한다 -> 레벨별로 출력
while(--size>=0) {
current = que.poll();
System.out.println(nodes[current]);
if(current*2<=lastIndex) //왼쪽자식
{
que.offer(current*2);
}
if(current*2+1<=lastIndex) //왼쪽자식
{
que.offer(current*2+1);
}
}
System.out.println();
++level;
}
}깊이 우선 탐색(DFS, Depth-First Search)
깊이 우선 탐색은 루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법 특히나 "맹목적인 탐색"을 하고자 할 때 사용할 수 있는 탐색 기법 입니다
-
핵심 아이디어
미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
→즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
-
사용하는 경우
모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
-
구현아이디어
- 스택의 최상단 노드를 확인
- 최상단 노드에게 방문하지 않은 인접 노드가 있으면 그 노드를 스택에 넣고 방문처리, 방문하지 않은 인접 노드가 없으면 최상단 노드를 스택에서 뺀다.
-
깊이 우선 탐색(DFS)의 특징
자기 자신을 호출하는 순환 알고리즘의 형태 를 가지고 있다.
전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.
이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
-
code
//전위 순회 public void dfs(int current) { if(current>lastIndex) return; //VLR System.out.println(nodes[current]); //방문 관련 처리 dfs(current*2); dfs(current*2+1); } //후위 순회 public void dfs2(int current) { if(current>lastIndex) return; //VLR dfs(current*2); dfs(current*2+1); System.out.println(nodes[current]); //방문 관련 처리 } //중위 순회 public void dfs3(int current) { if(current>lastIndex) return; //VLR dfs(current*2); System.out.println(nodes[current]); //방문 관련 처리 dfs(current*2+1); }
주제 : DP(Dynamic Programming)
문제 : 백준사이트 1965, 1535, 17212
DP란 ?
동태계획법은 동적계획법이라고도 하며 벨만(Bellman)에 의해서 고안된 것인데 재귀(再歸)라고 하는 수학적 개념에 기초를 두고 「최적성의 원리」에 따라 다단계의 결정과정을 취급하는 것이며 최대의 목재생산을 위한 간벌계획문제를 비롯해서 각종의 배분문제, 재고문제, 경제문제 등의 여러 가지 결정문제에 유용하게 쓰인다.출처: 네이버 지식백과
DP 해결방법
제가 생각하는 DP의 핵심은 큰문제를 작은 문제로 나누어 푸는 것입니다. 이때, 작은 문제들은 한번만 풀고 그 값을 저장하여 다른 큰 문제를 풀때 저장된 값을 이용하여 문제를 해결합니다. 그래서 DP의 많은 문제를 재귀를 이용하면 쉽게 해결 가능합니다.
DP를 사용해야하는 상황
아직 문제를 만났을때 DP로 풀어야하는지 아닌지 구분을 잘 못하지만 다른 사람들의 말은 빌어 얘기해보자면 하나의 큰문제를 작은 문제로 나눌수가 있다. 즉, 분기가 발생하는 문제에 쉽게 적용 할 수 있습니다.
DP에서 알아야할 핵심 개념
Memoization
메모이제이션은 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술이다. 메모아이제이션이라고도 한다.예시//before
fib(n) {
if n is 1 or 2, return 1;
return fib(n-1) + fib(n-2);
}
//after
fib(n) {
if memo[n] is zero:
memo[n] = fib(n-1) + fib(n-2);
return memo[n];
}해결 방법
DP는 크게 두가지 해결 방법이 있다.
Bottom-up
- 작은 문제에서 출발하여 큰 문제를 향해 가는 방식
- For문을 이용하여 처음값부터 다음값을 계산해 나가는 방식으로 구성
Top-Down
- (Top-Down)큰 문제에서 출발하여 작은 문제로 향해가는 방식
- 재귀와 같은 방식으로 위에서 아래로 내려오는 방식
- 함수 호출을 줄이기 위해 메모이제이션을 사용!
다익스트라(Dijkstra)알고리즘
최단 경로 탐색 알고리즘으로 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려줍니다. 다만 이떄의 음의 간선은 포함 할 수 없습니다. → 현실세계에서 사용하기에 매우 적합한 알고리즘
다익스트라 알고리즘은 다이나믹 프로그래밍으로도 볼 수 있다- > 최단 거리는 여러개의 최단 거리로 이루어져 있기때문에 작은 문제가 큰문제의 부분 집합에 속해 있다고 볼 수 있습니다. 기본적으로 다익스트라는 하나의 최단거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 특징이 존재한다.
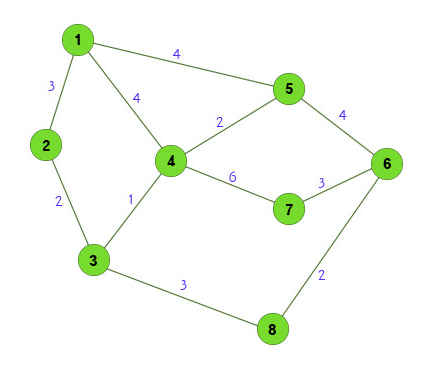
-
핵심 개념
현재까지 알고 있던 최단 경로를 계속해서 갱신해야한다.
-
구현아이디어
-
출발 노드를 설정합니다.
→distance는 처음에 나올 수 있는 가장 큰 값으로 초기화 해줍니다.
여기서는 Integer.MAX_VALUE 값으로 초기화 하겠습니다.
-
출발 노드를 기준으로 각 노드의 최소 비용을 저장합니다.
→시작노드의 거리를 0 으로 표시합니다(자기자신까지 거리는 0이므로)
그리고 시작노드의 check값을 true로 바꿔줍니다. (방문 한것이므로)
-
방문 하지 않은 노드 중에서 가장 비용이 적은 노드를 선택합니다.
시작노드와 연결되어 있는 노드들의 distance 값을 갱신합니다.
-
해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신합니다.
→ min_node와 연결된 노드들(방문하지 않은) distance 값을 갱신합니다.
-
3~4 반복
min_node의 check 값을 true로 변경합니다.
그리고 min_node와 연결된 노드들(방문하지 않은) distance 값을 갱신합니다.
이때 min_node와 연결된 distance 값이
distance[min_node] + (min_node와 그 노드의 거리)보다 큰 경우
distance값을 distance[min_node] +(min_node와 그 노드의 거리)로 갱신해줍니다.
-
Code
public class DijkstraAlgo { static class Graph{ private int n; //노드들의 수 private int maps[][]; //노드들간의 가중치 저장할 변수 public Graph(int n){ this.n = n; maps = new int[n+1][n+1]; } public void input(int i,int j,int w){ maps[i][j] = w; maps[j][i] = w; } public void dijkstra(int v){ int distance[] = new int[n+1]; //최단 거리를 저장할 변수 boolean[] check = new boolean[n+1]; //해당 노드를 방문했는지 체크할 변수 //distance값 초기화. for(int i=1;i<n+1;i++){ distance[i] = Integer.MAX_VALUE; } //시작노드값 초기화. distance[v] =0; check[v] =true; //연결노드 distance갱신 for(int i=1;i<n+1;i++){ if(!check[i] && maps[v][i] !=0){ distance[i] = maps[v][i]; } } for(int a=0;a<n-1;a++){ //원래는 모든 노드가 true될때까지 인데 //노드가 n개 있을 때 다익스트라를 위해서 반복수는 n-1번이면 된다. //원하지 않으면 각각의 노드가 모두 true인지 확인하는 식으로 구현해도 된다. int min=Integer.MAX_VALUE; int min_index=-1; //최소값 찾기 for(int i=1;i<n+1;i++){ if(!check[i] && distance[i]!=Integer.MAX_VALUE){ if(distance[i]<min ){ min=distance[i]; min_index = i; } } } check[min_index] = true; for(int i=1;i<n+1;i++){ if(!check[i] && maps[min_index][i]!=0){ if(distance[i]>distance[min_index]+maps[min_index][i]){ distance[i] = distance[min_index]+maps[min_index][i]; } } } } //결과값 출력 for(int i=1;i<n+1;i++){ System.out.print(distance[i]+" "); } System.out.println(""); } } public static void main(String[] args) { Graph g = new Graph(8); g.input(1, 2, 3); g.input(1, 5, 4); g.input(1, 4, 4); g.input(2, 3, 2); g.input(3, 4, 1); g.input(4, 5, 2); g.input(5, 6, 4); g.input(4, 7, 6); g.input(7, 6, 3); g.input(3, 8, 3); g.input(6, 8, 2); g.dijkstra(1); } }
-
플로이드 와샬(FLOYD WARSHALL) 알고리즘
다익스트라 알고리즘이 하나의 정점에서 출발했을때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이라면 플로이드 와샬 알고리즘은 모든 정점에서 모든 정점으로의 최단 경로를 구하는 알 고리즘입니다. 다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택했다면 플로이드 와샬 알고리즘은 기본적으로 거쳐가는 정점을 기준으로 알고리즘을 수행한다.
다익스트라 알고리즘과의 차이점
→간선의 가중치가 음이여도 상관없다
플로이드 와샬 알고리즘도 DP 기술에 의거하여 작은 문제로 큰문제를 해결해나가는 알고리즘입니다.
.png)
플로이드 와샬 알고리즘은 어떤것을 거쳐가는지
즉 x에서 Y로 가는 최소 비용 vs x에서 1로 가는 비용 + 노드 1 에서 Y로 가는비용
package com.study14;
public class floyd_warshall {
static int INF = 9999;
static int w[][] = {{0,5,INF,8}
,{7,0,9,INF}
,{2,INF,0,4}
,{INF,INF,3,0}}; //그래프는 7개의 정점을 가진다. 비방향그래프.}
public void printmatrix() {
for(int i=0; i<4; i++) {
for(int j=0; j<4; j++) {
if(w[i][j] == INF) {
System.out.printf(" INF"); continue;
}
System.out.printf("%4d",w[i][j]);
}
System.out.println();
}
}
public void floydalgorithm() {
for(int k=0; k<4; k++)
{
for(int i=0; i<4; i++)
{
for(int j=0; j<4; j++)
{
if(w[i][j]>w[i][k]+w[k][j])
w[i][j] = w[i][k]+w[k][j];
}
}
System.out.println(k +"번째 정점까지만 거칠수 있는 경우 모든 쌍에 대한 최단경로");
printmatrix();
}
}
public static void main(String[] args) {
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if(w[i][j] == INF) {
System.out.printf(" INF"); continue;
}
System.out.printf("%4d",w[i][j]);
}
System.out.println();
}
floyd_warshall f = new floyd_warshall();
f.floydalgorithm();
}
}
크루스칼 알고리즘(Kruskal Algorithm)
가장 적은 비용으로 모든 노드를 연결 하기 위해 사용하는 알고리즘
→ 최소 비용 신장 트리를 만들기 위한 대표적인 알고리즘입니다.
→예를 들어 여러개의 도시가 있을 떄 각 도시르 도로로 이용해 연결 하고자 할 때 들어가는 비용을 최소화 하기 위한 알고리즘입니다.
-
그래프 용어
노드 = 정점 = 도시: 그래프에서 동그라미에 해당하는 부분
간선 =거리 = 비용 : 그래프에서 선에 해당하는 부분
- 그래프 (노드 : 7 , 간선 11)
-
핵심 개념
간선을 거리가 짧은 순서대로 그래프에 포함시키는 방법
→싸이클이 형성되지 않아야한다.(3개 이상의 노드가 서로 연결 된 경우)
-
구현아이디어
- 정렬된 순서에 맞게 그래프에 포함 시킨다.
- 포함시키기 전에는 사이클 테이블을 확인합니다.
- 사이클을 형성하는 경우 간선을 포함하지 않습니다.


분발하세요