개인공부_4주차

전재우·2021년 2월 14일

2021년 2월 14일

4주차 리뷰

이번주는 설연휴가 있어 공부한 내용이 짧지만 굉장히 중요한 것들이 많이 있다. 오늘은 연휴가 끝나는 날인 일요일인데 연휴 전에 생각했던것보다 많은 것을 하지 않은것 같아 아쉬움이 조금 남는다. 한번에 확 몰아서 하는것보다 하루에 조금씩 꾸준히 채워 나가자!!

리스트

순서를 가진 데이터의 집합을 가리키는 추상자료형(abstract data type)
동일한 데이터를 가지고 있어도 상관없다
구현방법에 따라 크게 두가지로 나뉜다.
1. 순차 리스트: 배열을 기반으로 구현한 리스트 ( 원소 물리적 저장 순서 = 원소 논리적 순서)
2. 연결 리스트 : 메모리의 동적할당(객체 생성 동적 : heap)을 기반으로 구현된 리스트 ( 원소의 물리적 저장 순서 ≠ 원소 논리적 순서)

순차 리스트

구현 방법
1. 1차원 배열에 항목들을 순서대로 저장한다.
2. 데이터의 종류와 구조에 따라 구조화된 자료 구조를 만들어 배열로 만들 수 있다.
데이터 접근

배열의 인덱스를 이용해 원하는 위치의 데이터에 접근 할 수 있다.
삽입연산

삽입 위치의 다음의 항목들을 이동해야한다.
삭제연산

삭제 위치 다음의 항목들을 이동해야한다. ( 저장된 원소까지만 접근하게 해야한다.)
문제점

단순 배열을 이용해 순차리스트를 구현해 사용하는 경우, 자료의 삽입/삭제 연산과정에서 연속적인 메모리 배열을 위해 원소들을 이동시키는 작업이 필요하다.

원소의 개수가 많고 삽입/삭제 연산이 비번하게 일어날 수록 작업에 소요되는 시간이 크게 증가한다.

배열의 크기가 정해져 있는 경우 실제로 사용될 메모리 보다 크게 할당하여 메모리의 낭비를 초래할 수 도 있고 반대로 할당된 메모리보다 많은 자료를 사용하여 새롭게 배열을 만들어 작업해야하는 경우가 발생 할 수도 있다.

연결리스트

자료의 논리적인 순서와 메모리사이의 물리적인 순서가 일치하지 않고 개별적으로 위치하고 있는 원소의 레퍼런스를 연결하여 하나의 전체적인 자료구조를 이룬다.
링크를 통해 원소에 접근하므로, 순차리스트에서처럼 물리적인 순서를 맞추기위한 작업이 필요하지 않다.
자료구조의 크기를 동적으로 조정할 수 있어, 메모리의 효율적인 사용이 가능하다.
- 그림

### 노드

- 연결 리스트에서 하나의 원소에 필요한 데이터를 갖고 있는 자료단위
- 구성요소

    1)데이터 필드

    - 원소의 값을 저정하는 자료구조
    - 저장할 원소의 종류나 크기에 따라 구조를 정의하여 사용함.
    - 

    2) 링크 필드

    - 다음 노드의 주소를 저장하는 자료구조

### 헤드

- 리스트의 처음 노드를 가리키는 레퍼런스

### 연결 구조

- 노드가 하나의 링크 필드에 의해 다음 노드와 연결되는 구조를 가진다.
- 헤드가 가장 앞의 노드를 가리키고, 링크 필드가 연속적으로 다음 노드를 가리킨다.
- 최종적으로 NULL을 가리키는 노드가 리스트의 가장 마지막 노드다.

단순 연결리스트의 삽입연산 - 첫번째 노드 삽입

메모리를 할당하여 새로운 노드 new 생성

새로운 노드에 new의 데이터에 필드에 A를 저장

head에 저장된 주솟값을 새로운 노드 new의 링크 필드 값에 저장

4. head에 새로운 노드 new의 주소값을 저장

a원소를 가지고 있는 리스트의 첫번째에 c노드를 삽입할떄

메모리를 할당하여 새로운 노드 new 생성
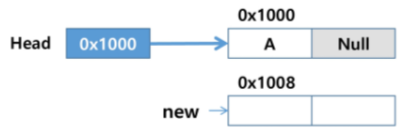
새로운 노드 new의 데이터 필드에 'C'저장
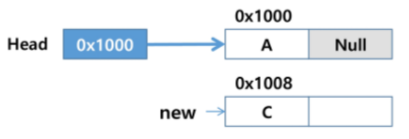
Head에 저장된 주소값을 새로운 노드의 링크 필드값에 저장

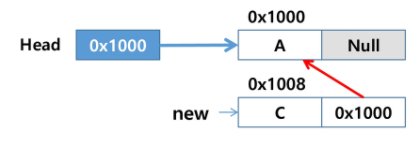
4.Head에 새로운 노드의 주솟값을 저장

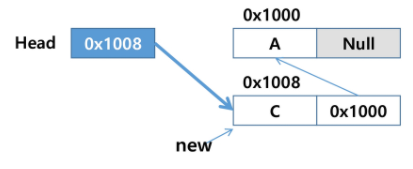
단순 연결리스트가 중간에 삽입 하려고 할때 앞에 연결된 연결리스트를 알아야하는 점을 보완하기 위해 이중 연결리스트로 해결 가능하다.

복습으로 한번 단순 연결리스트를 만들어 볼것( 첫번째 원소 삽입, 노드 값 탐색은 중요! 꼭 익히기)

이중 연결 리스트

양쪽 방향으로 순회할 수 있도록 노드를 연결한 리스트
두 개의 링크 필드와 한개의 데이터 필드로 구성
연결 구조

트리

비선형 자료 구조
원소들 간에 1:N 관계를 가지는 자료구조
원소들 간에 계층 관계를 가지는 계층형 자료구조
상위 원소에서 하위 원소로 내려가면서 확장되는 트리 모양의 구조
한개 이상의 노드로 이루어진 유한 집합이며 다음 조건을 만족한다.
1. 노드 중 최상위 노드를 루트(root)라 한다.
2. 나먼지 노드들은 N(≥0)개의 분리 집합 t1~tn으로 분리 될 수 있다.
이들 t1 ...tN은 각각 하나의 트리가 되며(재귀적정의) 루트의 부 트리(subtree)라 한다.

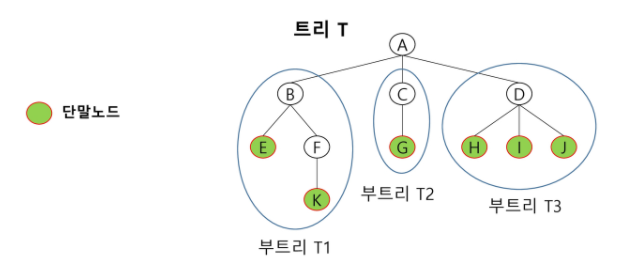
⇒ 궁극적으로 내가 표현하고 싶은 데이터들은 단말 노드에 담기는 경우가 많다.

노드(node)- 트리의 원소

트리 T의 노드 : A B C D E G H H I J K
형제 노드
- 같은 부모 노드의 자식들
- 형제 노드는 서로 간선이 없다 → 부모를 통해서 접근 해야한다.
- 형제 노드 사이에 간선이 존재하면 형제 노드가 아니다!
- ⇒ 간선이 존재한다는것은 상위 하위 개념이 존재한다는것
조상 노드
- 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
- K의 조상 F B A
자손 노드
- 서브 트리에 있는 하위 레벨의 노드들
- B의 자손 노드 - E F K
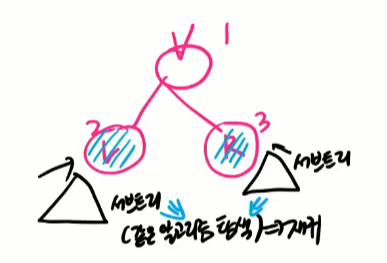
서브 트리(Subtree)
- 부모 노드와 연결된 간선을 끊었을 때생성되는 트리

⇒ 어떠한 노드 위치에서 subtree의 개수는 → 자식수 ⇒ 즉 간선의 수이다.

차수(degree)

노드의 차수 : 노드에 연결된 자식 노드의 수 (간선수) → B의 차수 = 2, C의 차수 = 1
트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰값(트리 T의 차수 = 3)
단말 노드(리프 노드) : 차수가 0인 노드 즉 , 자식 노드가 없는 노드

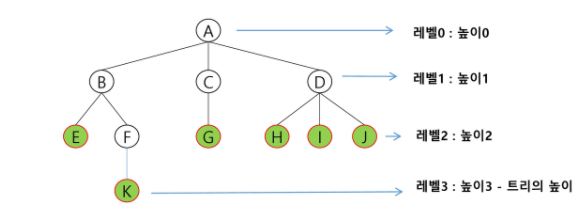
높이

노드의 높이 : 루트에서 노드에 이르는 간선의 수, 노드의 레벨(B의 높이 = 1, F의 높이 = 2)
트리의 높이 : 트리에 있는 노드의 높이 중에서 가장 큰값, 최대 레벨 (트리 T의 높이 = 3)

이진 트리

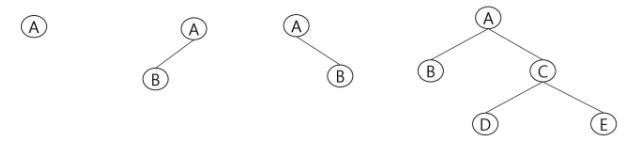
모든 노드들이 2개의 서브트리를 갖는 특별한 형태의 트리
각 노드가 자식 노드를 최대한 2개 까지만 가질 수 잇는 트리
- 왼쪽 자식 노드(left child node)
- 오른쪽 자식 노드(right child node)
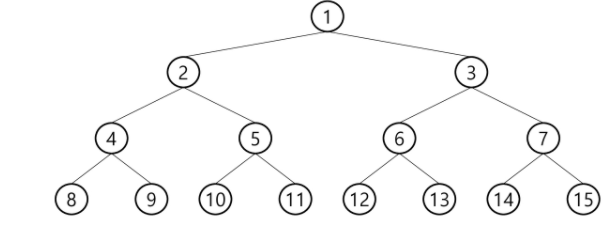
포화 이진 트리
- 모든 레벨에 노드가 포화상태로 차 있는 이진 트리
- 높이가 H일 때, 최대의 노드 개수인 (2^h+1 -1)의 노드를 가진 이진트리 ⇒ 높이가 3일때 = 15개의 노드
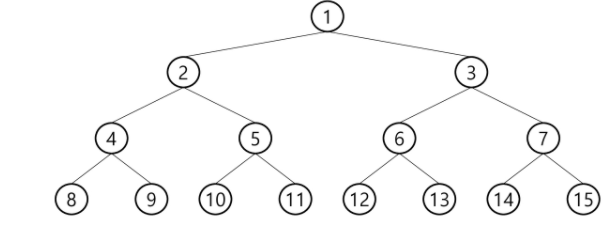
- 루트를 1번으로 하여 2^h+1 -1 까지 정해진 위치에 대한 노드 번호를 가진다
- ⇒ 루트부터 노드를 채우는방식

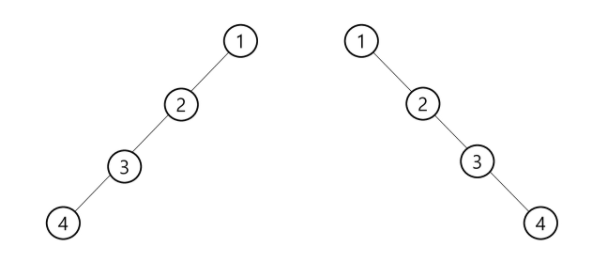
편향 이진 트리
- 높이 H에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드 만을 가진 이진 트리
- 왼쪽 편향 이진 트리
- 오른쪽 편향 이진 트리
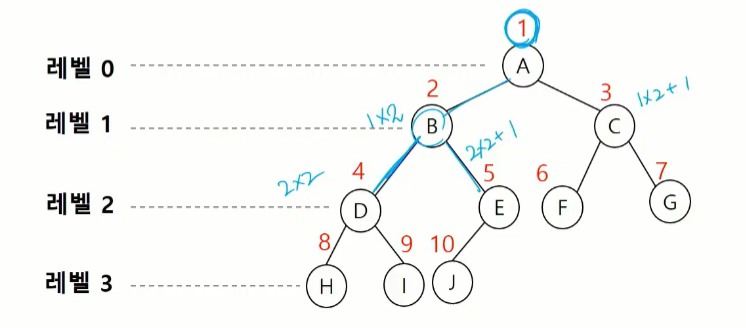
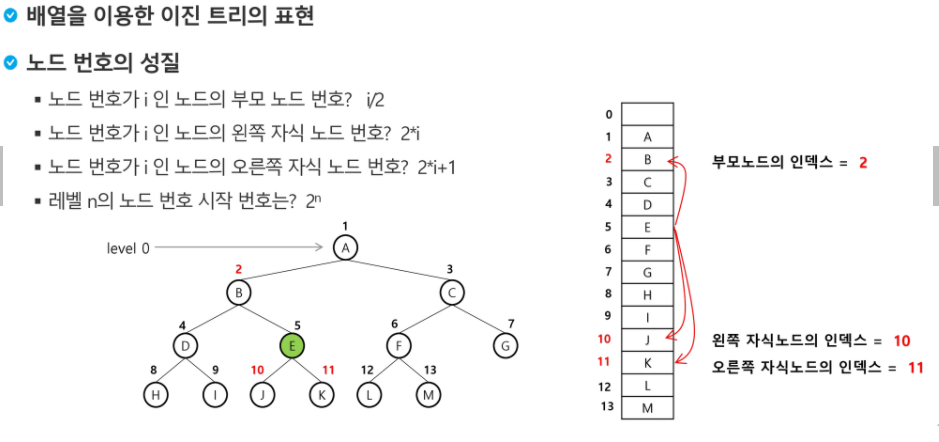
배열을 이용한 이진 트리의 표현
- 이진 트리에 각 노드 번호를 다음과 같이 부여
- 레벨 N에 있는 노드에 대하여 왼쪽부터 오른쪽 2^N 부터 2^n+1 -1까지 번호를 차례로 부여
- 루트의 번호를 1로 한다.
- 완전 이진 트리가 아닌 경우에는 높이가 h일떄 가질수 있는 포화 노드의 개수로 배열을 만든다.
- 왼쪽 자식은 내 노드 번호 x2 +1 , 오른쪽 자식은 내 노드 번호 x2 +1

배열을 이용한 이진 트리의 표현의 단점
- 편한 이진 트리의 경우 사용하지 않는 배열 원소에 대한 메모리 공간 낭비 발생
- 트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 삭제할 경우 배열의 크기 변경 어려워 비효율적

비선형 자료구조 완전 탐색

비선형 구조인 트리, 그래프의 각 노드(정점)을 중복되지 않게 전부 방문 하는것을 말하는데 비선형구조는 선형 구조에서와 같이 선후 연결 관계를 알 수 없다. 따라서, 특별한 방법이 필요하다
두가지 방법
- BFS 너비 우선 탐색(Breadth First Search)
- DFS 깊이 우선 탐색(Deep First Search)

너비 우선 탐색

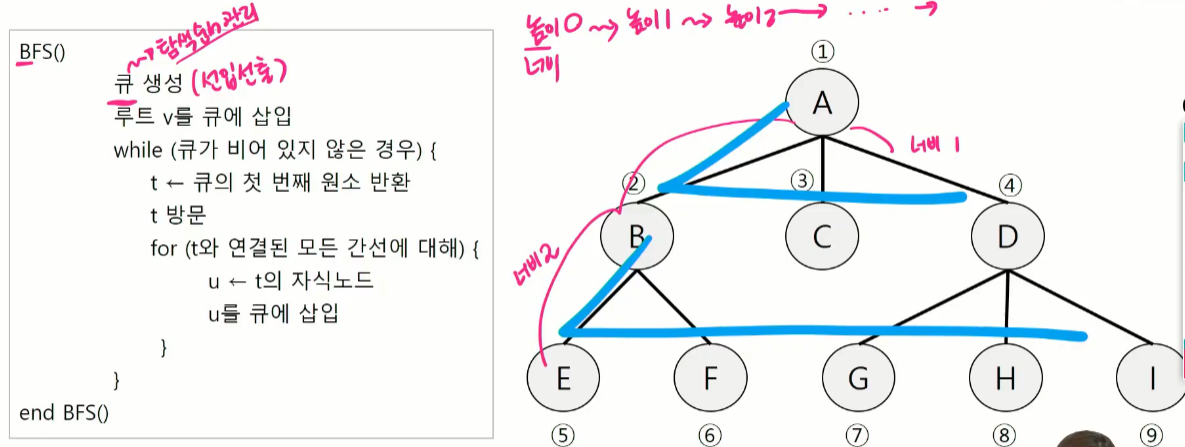
너비우선탐색은 루트 노드의 자식 노드들을 먼저 모두 차례로 방문한 후에, 방문했던 자식 노드들을 기준으로 하여 다시 해당 노드의 자식 노드들을 차례로 방문하는 방식
인접한 노드들에 대해 탐색을 한 후, 차례로 다시 너비우선탐색을 진행해야 하므로, 선입선출 형태의 자료구조인 큐를 활용함!
루트로 부터 손자노드로 접근하기 위해서는 자식노드에 방문했을때 손자 노드들을 기억 즉 가지고 있어야 접근 가능하다.

큐가 존재 할떄 A 를 방문 한경우 A의 자식 BCD를 큐에 집어 넣는다.

⇒ A B C D

| 너비 1|
A가 나가고 B에 방문한경우 EF를 큐에 집어 넣는다

⇒ B C D E F

C에 들어가도 자식이 없기때문에 따로 큐에 저장 x

C D E F

D를 방문한 경우

D E F G H I

| 너비 2 |

단말노드까지 진행

⇒ 너비가 0인 노드들이 너비가 1인 것들을 큐에 채우게 되고 너비가 1인것들이 너비가 2인것들을 큐에 채우게 된다.


import java.util.LinkedList;
import java.util.Queue;

public class CompleteBinaryTree {
	private char[] nodes;
	private int lastIndex;
	private final int SIZE;
	
	public CompleteBinaryTree(int size) {
		SIZE = size;
		nodes = new char[size+1];
	}
	public boolean isEmpty() {
		return lastIndex==0;
	}
	public boolean isFull() {
		return lastIndex == SIZE;
	}
	public void add(char e) {
		if(isFull()) {
		System.out.println("포화 상태입니다.");
		return;
		}
		nodes[++lastIndex] = e;
		
	}
	public void bfs() {
		if(isEmpty())return;
		//탐색 순서 번호를 큐로 관리
		Queue<Integer> que = new LinkedList<Integer>();
		que.offer(1);
		int current;
		while(!que.isEmpty()) {
			current = que.poll();
			System.out.println(nodes[current]);
			if(current*2<=lastIndex) //왼쪽자식
			{
				que.offer(current*2);
			}
			if(current*2+1<=lastIndex) //왼쪽자식
			{
				que.offer(current*2+1);
			}
		}
	}
	//너비 정보를 따로 갖고 있지 않고 레벨에따라 구분할수 있는 bfs 탐색
	public void bfs2() {
		if(isEmpty())return;
		
		Queue<Integer> que = new LinkedList<>();
		que.offer(1);
		int current,size,level=0;
		//탐색 순서 번호를 큐로 관리
		while(!que.isEmpty()) {
			//레벨
			//사이즈를 체크하고 
			size = que.size(); 
			System.out.println("level "+ level);
			//사이즈 만큼 체크한다 -> 레벨별로 출력
			while(--size>=0) {
			
				current = que.poll();
				System.out.println(nodes[current]);
				if(current*2<=lastIndex) //왼쪽자식
				{
					que.offer(current*2);
				}
				if(current*2+1<=lastIndex) //왼쪽자식
				{
					que.offer(current*2+1);
				}
				
			}
			System.out.println();
			++level;
		}
	}
}

디버그

시뮬레이션 문제를 풀때 행동들을 모두 메소드로 작성하는것이 디버그 할떄 유리하다 문제가 발견되지 않는 메소드이면 F6으로 넘어가기 쉽고 더 알고 싶은경우 F5로 들어가서 메소드의 변화를 찾으면 된다.
브레이크 포인트 오른쪽 클릭 → 브레이크포인트 프로퍼티스 → conditional을 이용해서 내가 원하는 조건을 만족할떄만 브레이크가 걸리게 할 수 있다

F5 → 메소드를 타고 들어감

F6 → 메소드를 타고 들어 가지 않고 다음 줄로 이동

F7 → 현재 함수 끝까지 바로 가서 리턴한 후 함수 호출

F8 은 다음 브레이크포인트로 가는것이 아니라 → 원래 실행하던대로 실행해라 대신, 브레이크포인트가 또 있다면 거기서 멈추게 됨.

(1) Skip All Breakpoints:모든 브레이크 포인트 건너뛰기

(2) Resume(F8키):멈추어 있던 쓰레드를 다시 진행시키고 다음 브레이크포인트까지 실행(3) Suspend:쓰레드를 일시 정지한다. 강제로 breakpoint를 현재 수행문에 지정한 것과 같다.

(4) Terminate:종료

(5) Step Into(F5키):프로그램을 한 스텝진행, 다음 실행 문이 함수 안이면 함수 안으로 들어감.(6) Step Over(F6키):함수 호출을 지나치고 현재 위치에서 한 스텝씩 진행(7) Step Return(F7키):현재 함수 끝까지 바로 가서 리턴한 후 함수 호출부로 되돌아 간다.(8) Drop to Frame:선택한 스택 프레임의 첫 행으로 실행 포인트를 옮긴다. 특정 함수를 실행하다 그 함수의 처음부터 다시 디버깅하려고 할때.(9) Use Step Filters(Shift+F5):스텝 필터링

DFS(Depth First Search)

깊이 우선 탐색
루트 노드에서 출발하여 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐새해 가다가 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 노드로 되돌아와서 다른 방향의 노드로 탐색을 계속 반복하여 결국 모든 노드를 방문하는 순회 방법
가장 마지막에 만났던 갈림길의 노드로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 재귀적으로 구현하거 나 후입선출 구조의 스택을 사용해서 구현

이진트리
- 순회(traversal)
  
  트리의 노드들을 체계적으로 방문하는것
- 3가지 기본적인 순회법
  
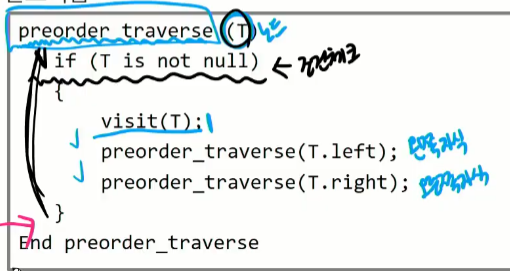
  전위순회
  
  부모노드 방문 후 , 자식노드들을 좌우 순서대로 방문
  - 수행방법
    1. 현재 노드 T를 방문하여 처리한다 → V
    2. 현재 노드 T의 왼쪽 서브트리로 이동한다 → L
    3. 현재 노드 T의 왼쪽 서브 트리로 이동한다 → R

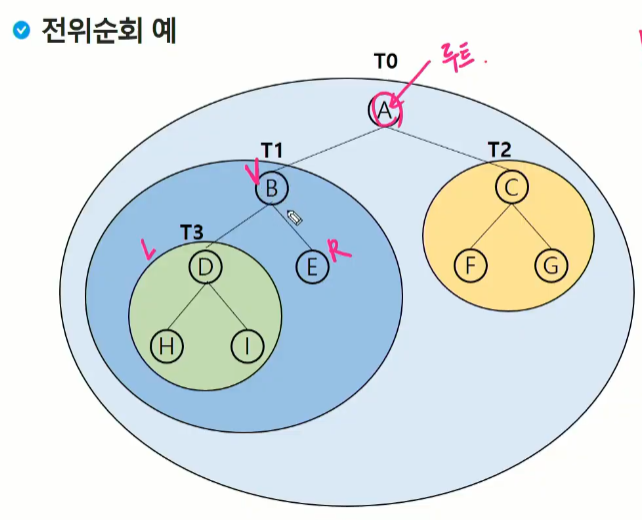
        순서 1 : A → T1→T2

        순서 2: A → B(T3) E → C F G

        총 순서 : → A B D H I E C F G

    ### 중위순회

    왼쪽자식 노드 , 부모노드 , 오른쪽 자식노드 순으로 방문한다.

    ### 후위순회

    자식노드를 좌우 순서로 방문한 후, 부모노드로 방문한다.

힙(heap)

완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료구조

최대 힙(max heap)
- 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
- 부모노드이 키 값 > 자식노드의 키 값
- 루트 노드 : 키 값이 가장 큰 노드
최소 힙(min heap)
- 키값이 가장 작은 노드를 찾기 위한 완전 이진트리
- 부모 노드의 키값 < 자식 노드의 키값
- 루트 노드 : 키 값이 가장 작은 노드

전재우

코린이

이전 포스트

CS스터디-2

다음 포스트