공부복습_5주차

전재우·2021년 2월 21일

2021년 02월 21일

SSAFY_4주차 리뷰

이번주는 졸업식이 있었다. 저번주 추석 연휴에 이어 졸업식에 와준 친구들과 함께 시간을 보내느라 황금같은 주말시간을 조금 허비 한것 같아서 싸피재우는 아쉽지만 인간전재우는 너무 행복했다. 일요일 점심부터 부랴부랴 복습하고 알고리즘을 문제를 풀고 있다 오늘 다시 마음을 꽉 잡고 26일날 있을 검정시험을 향해서 화이팅 하자!!

힙(heap)

완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료구조

최대 힙(max heap)
- 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
- 부모 노드의 키 값 > 자식노드의 키 값
- 루트 노드 : 키 값이 가장 큰 노드
최소 힙(min heap)
- 키값이 가장 작은 노드를 찾기 위한 완전 이진트리
- 부모 노드의 키값 < 자식 노드의 키값
- 루트 노드 : 키 값이 가장 작은 노드
힙 연산

삭제

힙에서는 루트 노드의 원소만 삭제 할 수 있다 → 최대/최소

루트 노드의 원솔르 삭제하여 반환한다.

힙의 종류에 따라 최대값 또는 최솟값을 구할 수 있다.
- 우선순위 큐를 구현하는 가장 효율적인 방법이 힙을 사용하는것이다.
  
  노드 하나의 추가 /삭제가 시간 복잡도가 O(logN)이거 최대값/ 최솟값을 O(1)에 구 할 수 있다.
  
  완전 정렬보다 관리비용이 적다.
- 배열을 통해 트리 형태를 쉽게 구현 할 수 있다.
  
  부모나 자식 노드를 O(1)연산으로 쉽게 찾을 수 있다
  
  n위치에 있는 노드의 자식은 2n 과 2n+1에 위치에 존재한다.
  
  완전 이진 트리의 특성에 의해 추가/삭제의 위치는 자료의 시작과 끝 인덱스로 쉽게 판단 할 수 있다.

우선순위 큐

PriorityQueue는 먼저 들어온 순서대로 데이터가 나가는 것이 아닌 우선순위를 먼저 결정하고 그 우선순위가 높은 엘리먼트가 먼저 나가는 자료구조입니다

우선순위 큐는 힙을 이용하여 구현
우선순위를 가진 항목들을 저장하는 큐
FIFO 순서가 아니라 우선순위가 높은 순서대로 먼저 나가게 된다.
데이터를 삽입할 때 우선순위를 기준으로 최대힙 혹은 최소 힙을 구성하고 데이터를 꺼낼 때 루트 노드를 얻어낸 뒤 루트 노드를 삭제할 때는 빈 루트 노드 위치에 맨 마지막 노드를 삽입한 후 아래로 내려가면서 적절한 자리를 찾아서 옮기는 방식으로 진행됩니다.
특징
1. 높은 우선순위의 요소를 먼저 꺼내서 처리하는 구조 (큐에 들어가는 원소는 비교가 가능한 기준이 있어야함)
2. 내부 요소는 힙으로 구성되어 이진트리 구조로 이루어져 있음
3. 내부구조가 힙으로 구성되어 있기에 시간 복잡도는 O(NLogN)
4. 응급실과 같이 우선순위를 중요시해야 하는 상황에서 쓰임

import java.util.PriorityQueue; //import

//int형 priorityQueue 선언 (우선순위가 낮은 숫자 순)
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();

//int형 priorityQueue 선언 (우선순위가 높은 숫자 순)
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(Collections.reverseOrder());

//String형 priorityQueue 선언 (우선순위가 낮은 숫자 순)
PriorityQueue<String> priorityQueue = new PriorityQueue<>(); 

//String형 priorityQueue 선언 (우선순위가 높은 숫자 순)
PriorityQueue<String> priorityQueue = new PriorityQueue<>(Collections.reverseOrder());

java.utill.priorityQueue()

원소들의 natural ordering에 따라 heap 유지
따라서, 반드시 모든 원소는 comparable 인터페이스를 구현해야함 (compareto (to))

java.utill.priorityQueue(Comparator comparator)→비교 도우미

명시된 Comparator의 구현에 따라 원소들의 순서를 유지 compare(to1 , to2)

Comparable

int compareTo(T other)
자신과 인자로 전달 받은 타 원소와 비교하여 정수리턴
- 음수결과 : 타 원소가 크다 → 정렬사용시 에서 그대로 유지
- 0의 결과 : 둘이 같다. → 정렬사용시 에서 그대로 유지
- 양수 결과 : 자신이 크다. → 정렬사용시 에서 그대로 유지

compareTo( ) 메소드에서

오름차순의 결과를 원할 경우 : 내꺼 - 남의꺼
내림차순의 결과를 원할 경우 : 남의꺼 - 내꺼

Comparator

int Compare(t1, t2)
비교 대상의 두 원소가 아닌 별도의 도우미 역할
두원소 비교하여 정수 리턴
- 음수 결과 : t2 원소가 크다
- 0결과 : 둘이 같다
- 양수 결과 : t1원소가 더크다

우선 순위를 처리하는 세가지 방법

public class WriterTest {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		ArrayList<Writer> list = new ArrayList<>();
		list.add(new Writer(3,"tommy",35,"hello java"));
		list.add(new Writer(2,"jane",30,"stop java"));
		list.add(new Writer(1,"bill",45,"sing java"));
		list.add(new Writer(5,"kim",15,"bye java"));
		list.add(new Writer(4,"tommy",65,"master java"));
		
		//Arrays.sort(a);
		// list: Comparable 타입의 객체 이어야 한다 -> Comparable 을 implements해야한다
		Collections.sort(list);
		for(Writer w : list) {
			System.out.println(w);
		}
		System.out.println();
		//이름순으로 정렬하는 방법 -> 사전순
		Collections.sort(list,new WriterNameComparator());
		
		for(Writer w : list) {
			System.out.println(w);
		}
		//나이 기준으로 정렬 Compartor객체 지정
		Collections.sort(list,new Comparator<Writer>() {//Comparator를 impl하는 익명객체

			@Override
			public int compare(Writer o1, Writer o2) {
				// TODO Auto-generated method stub
				return o1.age - o2.age;
			} 
			
		});
  	 	 //람다를 이용한 compartor 객체 지정
		;Collections.sort(list,(o1,o2)->{
			return o1.age - o2.age ;
			
		});
	}


/*interface : Comparable , Comparator
 * 객체의 정렬과 관련된 인터페이스
 * Comparable : 클래스 내부에  객체의 정렬 기준을 만들때 즉, 클래스를 설계하면서 정렬할 기준을 클래스 내부에 정의 해놓는것
 * Comparator : 클래스 외부에 객체의 정렬 기준을 만들어 놓을때 사용됨. 
 * */
public class Writer implements Comparable<Writer>{
	int num;
	String name;
	int age;
	String title;
	public Writer(int num, String name, int age, String title) {
		super();
		this.num = num;
		this.name = name;
		this.age = age;
		this.title = title;
	}
	@Override
	public String toString() {
		StringBuilder builder = new StringBuilder();
		builder.append("Writer [num=");
		builder.append(num);
		builder.append(", name=");
		builder.append(name);
		builder.append(", age=");
		builder.append(age);
		builder.append(", title=");
		builder.append(title);
		builder.append("]");
		return builder.toString();
	}
	@Override
	public int compareTo(Writer other) {
		//int result = this.num - other.num;//num 기준 오른차순
		int result = other.num-this.num; //num 기준 내림차순
		return result;
	}
	
}


import java.util.Comparator;

//wtier 클래스의 name을 기준으로 비교 후 정렬시켜 주는 클래스
public class WriterNameComparator implements Comparator<Writer>{

	@Override
	public int compare(Writer o1, Writer o2) {
		// TODO Auto-generated method stub
		int result = o1.name.compareTo(o2.name);
		if(result == 0)
			return o1.title.compareTo(o2.title); //2번째 정렬기준 이름이 같은 경우 제목으로 비교
			
		
		return 0;
	}

}

완전 탐색(Exhaustive Search)

완전 검색 방법은 문제의 해법으로 생각 할 수 잇는 모든 경우의 수를 나열해보고 확인하는 기법이다.
Brute-force 혹은 generate-and-test 기법이라고도 불리운다.
- just-do-it
- force의 의미는 사람 보다는 컴퓨터의 force를 의마한다.
모든 경우의 수를 테스트한 후 , 최종 해법을 도출한다
상대적으로 빠른 시간에 문제 해결(알고리즘 설계)을 할 수 잇다.
일반적으로 경우의 수가 상대적으로 작을때 유용하다.
모든 경우의 수를 생성하고 테스트하기때문에 수행 속도는 느리지만 해답을 찾아내지 못할 확률이 작다.
검정등에서 주어진 문제를 풀떄, 우선 와전 검색으로 접근하여 해답을 도출한 후 , 성능 개선을 위해 다른 알고리즘을 사용하고 해답을 확인하는것이 바람직하다.

완전 탐색

많은 종류를 특정 조건을 만족하는 경우나 요소를 찾는것이다.
순열 조합 그리고 부분집합과 같은 조합적 문제들과 연관된다.

순열(permutation)

서로 다른 것들 중 몇개를 뽑아서 한줄로 나열하는것
서로 다른 n개 중 r개를 택하는 순열 nPr
boolean형 배열을 사용해서 순열을 표현한 경우

import java.util.Arrays;

import com.ssafy.exhausitive.PermutationTest;
//3자리수 수열

public class PermuationTest {
	static int N = 3,R=3;
	static int[] result,numbers;//뽑힌 숫자 담을 배열
	static boolean[] isSelected; //N 개중 선택된 숫자 표시(true, false) 배열
	
	public static void main(String[] args) {
		result = new int [R];
		numbers = new int [N];
		for (int i = 0; i < numbers.length; i++) {
			numbers[i]=i+1;//1,2,3
			
		}
		isSelected = new boolean[N]; //all false
		permutation(0);
	}
	//현재까지 뽑힌 숫자 갯수를 입력받아 체크하고
	//아직 뽑아야 하는 숫자가 남았으면 뽑기
	public static void permutation(int cnt) {
		if(cnt == R ) {//다 뽑았으면
			System.out.println(Arrays.toString(result));//결과 출력
			return;
		}
		
		for (int i = 0; i < N; i++) {//모든 숫자를 대상으로 작업
			if(!isSelected[i]) { //뽑히지 않앗다면
				isSelected[i] = true;//i번째 숫자 사용함을 알리는것
				result[i]=numbers[i];
				permutation(cnt+1);
				isSelected[i] = false;
				
			}
		}
	}
}

비트마스킹을 통한 순열 생성 - 비트연산자를 사용

import java.util.Arrays;

import com.ssafy.exhausitive.PermutationTest;
//3자리수 수열

public class PermuationBitmaskTest2 {
	static int N = 3,R=3;
	static int[] result,numbers,input[];//뽑힌 숫자 담을 배열
	static boolean[] isSelected; //N 개중 선택된 숫자 표시(true, false) 배열
	
	public static void main(String[] args) {
		result = new int [R];
		numbers = new int [N];
		for (int i = 0; i < numbers.length; i++) {
			numbers[i]=i+1;//1,2,3
			
		}
		isSelected = new boolean[N]; //all false
		permutation(0,0);
	}
	//현재까지 뽑힌 숫자 갯수를 입력받아 체크하고
	//아직 뽑아야 하는 숫자가 남았으면 뽑기
	//비트연산자 추가
	public static void permutation(int cnt, int flag) {
		if(cnt == N ) {//다 뽑았으면
			System.out.println(Arrays.toString(result));//결과 출력
			return;
		}
		
		for (int i = 0; i < N; i++) {//모든 숫자를 대상으로 작업
			if((flag & 1<<i) != 0) continue; //사용여부 체크
			
				//numbers[cnt] = input[i]//i번째 숫자 사용함을 알리는것
				result[i]=numbers[i];
				permutation(cnt+1, flag | 1<<i); // 사용하는 처리 즉 visit 처리 
		}
	}
}

비트연산자

nextPermutation

nPr에서 사용 불가능

nPn에서 사용 가능

현 순열에서 사전 순으로 다음 순열 생성

가장 작은 순열은 → nextpermutation 시작전에 가장 작은 순열을 만들어주고 시작해야한다

→ 사용 전에 숫자 배열은 오름차순으로 정렬하여 가장 작은 순열 한번 처리

알고리즘
- 아래 과정을 반복하여 사전식으로 다음으로 큰 순열 생성 ( 가장 큰 내림차순 순열을 만들 때 까지 반복한다.)
  
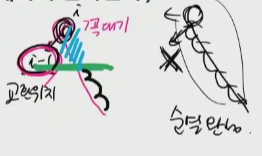
  1.뒤쪽으로 탐색하며 교환위치(i-1) 찾기 i =꼭대기
  1. 뒤쪽부터 탐색하여 교환위치(i-1)와 교환할 큰 값 위치(j)찾기 (자신보다 다음으로 큰수) → i-1교환위기 값보다 큰값 항상 존재한다!
  2. 두 위치 값(i-1,j) 교환
  3. 꼭대기 위치(i) 부터 맨 뒤 까지 오름차순 정렬

import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.Scanner;

public class P4_PermuationNPTest2 {
	static int N;
	static int [] input;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		input = new int[N];
		
		for (int i = 0; i < N; i++) {
			input[i]=sc.nextInt();
		}
		//오름차순 정렬
		Arrays.sort(input);
		System.out.println(Arrays.toString(input));
		System.out.println("===============");
		do {
			//실제로는 작업할 부분 
			System.out.println(Arrays.toString(input));
		}while(NextPermutation());
	}
	public static boolean NextPermutation() {
		//맨뒤부터 사용
		//1.뒤쪽부터 탐색하며 교환위치(i-1) 찾기 i 는 꼭대기
		int i = N-1;
		while(i>0 && input[i-1]>= input[i] ) --i;
		
		//더이상 앞자리가 없는 상황 : 현 순열의 상태가 가장 큰 순열(마지막순열)
		if(i==0) return false;
		//맨뒤부터 사용
		//2.뒤쪽부터 탐색하며 교환위치(i-1)과 교환할 큰 값 위치(j) 찾기
		int j = N-1;
		while(input[i-1] >= input[j]) --j;
		//3.두 위치 값 (i-1,j) 교환
		swap(i-1,j);
		
		//맨뒤부터 사용	
		//4.꼭대기 위치(i)부터 맨뒤까지 오름차순 정렬 
		int k = N-1;
		while(i<k) {
			swap(i++,k--);
			 
		 }
		return true; 
	}
	private static void swap(int i , int j) {
		int temp = input[i];
		input[i] = input[j];
		input[j] = temp;
	}
}

i값 찾기 (i-1)번째가 교환 대상
- 1 2 3 4 5 / 4가 교환 위치 5가 꼭대기
j값 찾기 (맨뒤~i-1보다 큰값위치)

(i-1) → (j)

1 2 3 5 4
swap

12453
정렬

꼭대기위치(i) 부터 맨뒤까지 오름차순 정렬

12435

NextPermutation 을 이용한조합

NextPermutation으로 조합을 해결하기 위해서는 사용하고 안하고를 np를 돌려서 조합의 수로 사용한다

즉 0 0 0 0 이라는 배열에 2개의 수만 고르고 싶다면 00 11 로 초기화 해주고 그것에 np를 돌리게 되면 조합을 해결 할 수있다.


import java.util.Arrays;
import java.util.Scanner;

public class C2_combinationNextPermutationTest2 {
	static int N,R;
	static int[] input;
	static int[] isSelected;
	
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		R = sc.nextInt();
		
		input = new int[N];
		isSelected = new int[N]; // N 크기의 flag 배열
		
		for (int i = 0; i < N; i++) {
			input[i] = sc.nextInt();
		}
		int cnt = 0;
		while(++cnt<=R) isSelected[N-cnt]=1; //조합을 찾을 R개만큼 1로 채운다.
		
		do {
			for (int i = 0; i < N; i++) {
				if(isSelected[i]==1)System.out.print(input[i]+ " ");
			}
			System.out.println();
		}while(NextPermutation());
	}
	public static boolean NextPermutation() {
		//맨뒤부터 사용
		//1.뒤쪽부터 탐색하며 교환위치(i-1) 찾기 i 는 꼭대기
		int i = N-1;
		while(i>0 && isSelected[i-1]>= isSelected[i] ) --i;
		
		//더이상 앞자리가 없는 상황 : 현 순열의 상태가 가장 큰 순열(마지막순열)
		if(i==0) return false;
		//맨뒤부터 사용
		//2.뒤쪽부터 탐색하며 교환위치(i-1)과 교환할 큰 값 위치(j) 찾기
		int j = N-1;
		while(isSelected[i-1] >= isSelected[j]) --j;
		//3.두 위치 값 (i-1,j) 교환
		swap(i-1,j);
		
		//맨뒤부터 사용	
		//4.꼭대기 위치(i)부터 맨뒤까지 오름차순 정렬ㄴㄴ  
		int k = N-1;
		while(i<k) {
			swap(i++,k--);
			 
		 }
		return true; 
	}
	private static void swap(int i , int j) {
		int temp = isSelected[i];
		isSelected[i] = isSelected[j];
		isSelected[j] = temp;
	}
	
	// 전역변수를 사용하지 않고 사용할 배열을 이용할떄 배열을 매개변수로 넘겨주어서 사용하는방법 (헷갈릴경우
	// 교환이 이루어져야할 배열을 생각해보자
	public static boolean NextPermutation2(int[] arr) {
		//맨뒤부터 사용
		//1.뒤쪽부터 탐색하며 교환위치(i-1) 찾기 i 는 꼭대기
		int i = N-1;
		while(i>0 && arr[i-1]>= arr[i] ) --i;
		
		//더이상 앞자리가 없는 상황 : 현 순열의 상태가 가장 큰 순열(마지막순열)
		if(i==0) return false;
		//맨뒤부터 사용
		//2.뒤쪽부터 탐색하며 교환위치(i-1)과 교환할 큰 값 위치(j) 찾기
		int j = N-1;
		while(arr[i-1] >= arr[j]) --j;
		//3.두 위치 값 (i-1,j) 교환
		swap2(arr,i-1,j);
		
		//맨뒤부터 사용	
		//4.꼭대기 위치(i)부터 맨뒤까지 오름차순 정렬ㄴㄴ  
		int k = N-1;
		while(i<k) {
			swap2(arr,i++,k--);
			 
		 }
		return true; 
	}
	private static void swap2(int[] arr,int i , int j) {
		int temp = arr[i];
		arr[i] = arr[j];
		arr[j] = temp;
	}
}

NextPermutation을 이용한 부분집합 생성

바이너리 카운팅(binary Counting)

이진수의 경우 이미 비트마스킹하는것처럼 움직이기 때문에 사용을 확인하는 체크(flag & 1<<i)만 이용하면 된다. → 방문 표시(flag | 1<<i)가 필요가 없다.


import java.util.Arrays;
import java.util.Scanner;

public class S2_BinaryCountingTest {

static int N;
static int [] input;

private static void generateSubset(int caseCount) {
	for (int flag = 0; flag < caseCount; flag++) { //flag : 비트마스크되어 있는 수 
		for (int j = 0; j < N; j++) { // 맨뒤부터 N개의 비트열을 확인한다.
			if((flag & 1 <<j) != 0) {
				System.out.print(input[j]+ " ");
			}else
			{
				System.out.print("X ");
			}
			
		}
		System.out.println();
	}
}
public static void main(String[] args) {
	Scanner sc = new Scanner(System.in);
	N = sc.nextInt();
	input = new int[N];
	
	for (int i = 0; i < N; i++) {
		input[i]=sc.nextInt();
	}
	generateSubset(1<<N); //1<<N 2^n을 구하는 방법
}

}

탐욕(greedy) 알고리즘

문제 제시 : 거스름돈 줄이기

탐욕 알고리즘은 최적해를 구하는데 사용되는 근시안적인 방법
최적화 문제(optimization)이란 가능한 해들 중에서 가장 좋은(최대 또는 최소) 해를 찾는 문제이다.
일반적으로, 머리 속에 떠오르는 생각을 검증없이 바로 구현하면 greedy 접근이 된다.
여러 경우 중 하나를 선택할 때마다 그 순간에 최적이라고 생각되는것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다.
각선택 시점에서 이루어지는 결정은 지역적으로는 최적이지만, 그선택들을 계속 수집하여 최종적으로 해답을 만들었다고 하여, 그것이 최적이라는 보장이 없다!
일단, 한번 선택된 것은 번복하지 않는다. 이런 특성 때문에 대부분의 탐욕 알고리즘들은 단순하며, 또한 제한적인 문제들에 적용된다.
필수 요소
- 탐욕적 선택 속성
  - 탐욕적 선택은 최적해로 갈수 있음을 보여라 → 즉 탐욕적 선택은 항상 안전하다
- 최적 부분구조
  - 최적화 문제를 정형화하라→ 하나의 선택을 하면 풀어야할 하나의 하위 문제가 남는다.
  
  ⇒ 원문제의 최적해 = 탐욕적 선택 + 하위 문제의 최적해 임을 증명하라!!

배낭 짐싸기(Knapsack)

도둑은 부자들의 값진 물건들을 훔치기 위해 보관창고에 침입하였다.
도둑은 훔친 물건을 배낭에 담아 올 계획이다. 배낭은 담을 수 잇는 물건의 총 무가게 정해져있다.
창고에는 여러 개의 물건들이 있고 각각의 물건에는 무게와 값이 정해져 잇다.
경비원들에 발각되기 전에 배낭이 수용할 수 있는 무게를 초과하지 않으면서, 값이 최대가 되는 물건들을 담아야한다.

Knapsack 문제유형

0-1 Knapsck
- 배낭에 물건을 통째로 담아야하는 문제
- 물건을 쪼갤 수 없는 경우
Fractional Knapsack
- 물건을 부분적으로 담는것이 허용되는 문제
- 물건을 쪼갤 수 있는 경우
해결 아이디어
1. 가능한 모든 집합 다 고려 ⇒ 부분집합 powerSet (공집합 제외)
  
  제한사항 : 크기가 n인 부분합의 수 2^n ⇒ n의 크기가 최대 20 이하일 경우 만 사용가능

0-1 Knapsack에 대한 완전 검색 방법

완전 검색으로 물건들의 집합 S 에 대한 모든 부분집합을 구한다.
부분집합의 총 무게가 W를 초과하는 집합들은 버리고, 나머지 집합에서 총 값이 가장 큰 집합을 선택 할 수 있다.
물건의 개수가 증가하면 시간 복잡도가 지수적으로 증가하낟.
- 크기가 n인 부분합의 수 2^n ⇒ n의 크기가 최대 20 이하일 경우 만 사용가능
탐욕적 방법 1

탐욕적 방법 2

탐욕적 방법 3

Fractional Knapsack에 대한 GREEDY한 방법

MeetingRoom greedy한 해결


import java.lang.reflect.Array;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
/*
10
1 1 4
2 1 6
3 6 10
4 5 7
5 3 8
6 5 9
7 3 5
8 8 11
9 2 13
10 12 14
*/

public class MeetingRoomTest {
	static class MeetingRoom implements Comparable<MeetingRoom>{
		int num,start,end;

		public MeetingRoom(int num, int start, int end) {
			super();
			this.num = num;
			this.start = start;
			this.end = end;
		}
		//종료시간이 빠르순으로 정렬한경우 
// (1,1,2) (2,2,3) (3,3,3) //3개 가능
// (1,1,2) (3,3,3) (2,2,3) //2개 가능
		//-> 종료시간이 같은경우 시작시간이 빠른순으로 정렬
		@Override
		public int compareTo(MeetingRoom o) {
			int diff = this.end - o.end;
			return diff!=0? diff : this.start-o.start;
		}
		@Override
		public String toString() {
			StringBuilder builder = new StringBuilder();
			builder.append("MeetingRoom [num=");
			builder.append(num);
			builder.append(", start=");
			builder.append(start);
			builder.append(", end=");
			builder.append(end);
			builder.append("]");
			return builder.toString();
		}
		
	}
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		MeetingRoom[] m = new MeetingRoom[N];
		
		for (int i = 0; i < N; i++) {
			m[i] = new MeetingRoom(sc.nextInt(), sc.nextInt(), sc.nextInt());
			
		}
		List<MeetingRoom> list = getSchedule(m);
		for (MeetingRoom meetingRoom: list) {
			System.out.println(meetingRoom);
		}
	}
	public static List<MeetingRoom> getSchedule(MeetingRoom[] m){
		ArrayList<MeetingRoom> list = new ArrayList<MeetingRoom>(); //배정된 회의
		Arrays.sort(m);
		list.add(m[0]);
		
		for (int i = 0,size=m.length ; i < size; i++) {
			if(list.get(list.size()-1).end <= m[i].start){
				list.add(m[i]);
			}
		}
		return list;
	}
	
}

분할 정복

예시)

분할정복 기법

설계전략
- 분할(Divide) : 해결할 문제를 여러 개의 작은 부분으로 나눈다.
- 정복(Conquer) 나눈 작은 문제를 각각 해결한다.
- 통합(Combine) : (필요하다면) 해결된 해답을 모은다.
Top-down Approach

이진 탐색

자료의 가운데에 있는 항목의 키값과 비교하여 다음 검색의 위치를 결정하고 검색을 계속 진행하는 방법

목적 키를 찾을 때까지 이진 검색을 순환적으로 반복 수행함으로서 검색 범위를 반으로 줄여가면서 보다 빠르게 검색을 수행함
이전 검색을 사용하기 위해서는 자료가 정렬된 상태여야한다.
검색과정
1. 자료의 중앙에 있는 원소를 고른다.
2. 중앙 원소의 값과 찾고자 하는 목표 값을 비교한다.
3. 중앙 원소의 값과 찾고자 하는 목표 값이 일치하면 탐색을 끝낸다.
4. 목표 값이 중앙 원소의 값보다 작으면 자료의 왼쪽 반에 대해서 새로 검색을 수행하고, 크다면 자료의 오른쪽 반에 대해서 새로 검색을 수행한다.
5. 찾고자 하는 값을 찾을때 까지 위의 과정을 반복한다.
- 예시

    - 예시

        더이상 나눌수가 없는 경우 → 검색 실패

          package com.ssafy.divide;

           import java.util.Arrays;

           public class D2_BinarySearchTest {

           	public static void main(String[] args) {
           		// TODO Auto-generated method stub
           		int[] arr = {3,11,15,20,21,29,45};
           		//이진 탐색에서는 정렬이 필수!
           		Arrays.sort(arr);
           		System.out.println(binarySearch(arr,15));
           		System.out.println(binarySearch(arr,15,0,arr.length-1));
           		
           		System.out.println(binarySearch(arr,45));
           		System.out.println(binarySearch(arr,45,0,arr.length-1));
           		
           		
           		//Arrays.binarySearch API가 존재한다.(배열 전체를 주는부분)
           		System.out.println(Arrays.binarySearch(arr, 15));
           		
           		//범위를 주고 이진탐색 대신 end를 줄떄 -1 하지 않아도 된다. arr.length값 직전까지만 탐색하기때문에 
           		//즉 0은 크거나 같고 , ARR.LENGTH는 그것보다 작을때 까지 탐색
           		System.out.println(Arrays.binarySearch(arr, 0,arr.length,45));
           		
           	
           		// 	Arrays.binarySearch 못찾은 경우 리턴 값으로 -insertionpoint-1을 준다 즉 있어야할 자리를 인덱스에 -1에 한값을  음수로 준다  
           		//해당하는 인덱스의 음수값으로 주지 않는 이유는 0인덱스가 올 가능성이 있기떄문에 -1한 값을 준다. 즉 0인덱스인 경우 찾은 경우인지 못찾은 경우인지 알지 못한다.
           		//해당하는 위치에 삽입 하고 싶을경우 절대값을 취한 다음에 -1을 해서 해당 인덱스에 삽입 가능하다.
           		System.out.println(Arrays.binarySearch(arr, 14));
           	}
           	
           	//반복
           	private static int binarySearch(int[] arr , int key) {
           		int start = 0, end =arr.length-1;
           		
           		
           		while(start<=end) {
           		//탐색 범위의 중간값을 구하는 과정
           		int mid = (start + end)/2;
           		
           		//구한 중간값이 내가 찾고자하는 값인 경우
           		if(arr[mid]==key) return mid;
           		
           		//내가 찾고하는 값이 더 큰경우
           		else if(arr[mid]<key) start=mid+1;
           		//내가 찾고하는 값이 더 작은 경우
           		else if(arr[mid]>key) end=mid-1;
           		
           		}
           		//값을 찾지 못한 경우
           		return -1;
           	}
           	//재귀 오버로딩!
           	private static int binarySearch(int[] arr,int key,int start,int end) {
           		if(start<=end) {
           		//탐색 범위의 중간값을 구하는 과정
           		int mid = (start + end)/2;
           		
           		//구한 중간값이 내가 찾고자하는 값인 경우
           		if(arr[mid]==key) return mid;
           		
           		//내가 찾고하는 값이 더 큰경우
           		else if(arr[mid]<key) return binarySearch(arr,key,mid+1,end);
           		//내가 찾고하는 값이 더 작은 경우
           		else if(arr[mid]>key) return binarySearch(arr,key,start,mid-1);
           		}
           		return -1;
           		
           	}
           }

백트래킹

다 퀸을 가능한 자리에 놓아보는 완전 탐색에서 출발한다.

N Queen 문제
- 퇴각탐색→ 백트레킹
- 모든 조합을 시도해서 문제의 해를 찾는다. → 상태공간트리의 모든 가능성을 하나씩 선택하면서 해를 찾아감(완전 탐색)
- 해를 얻을떄까지 모든 가능성을 시도한다.
- 모든 가능성은 하나의 트리처럼 구성할 수 있으며, 선택지 중에 해결책이 있다.
- 여러가지 선택지들이 존재하는 상황에서 하나의 가지를 선택한다.
  
  1열에서 N열에 놓기 →하나의 가지 선택 → 가지치기
- 선택이 이루어지면 새로운 선택지들의 집합이 생성된다.
- 이런 선택을 반복하면서 최종 상태에 도달한다.
- 보통 재귀 함수로 구현된다. → BFS를 사용한다.
상태 공간트리 탐색은 →DFS를 사용해서 탐색

당첨 리프 노드 찾기
루트에서 갈 수 있는 노드를 선택한다.
- 꽝 노드까지 도달하면 최근의 선택으로 되돌아와서 다시 시작한다.
- 더이상 선택지가 없다면 이전의 선택지로 돌아가서 다른 선택을 한다.
- 루트까지 돌아갔을 경우 더 이상 선택지가 없다면 찾는 답이 없다.

8-Queens 문제

퀸 8개를 크기 8의 체스판 안에 서로를 공격 할 수 없도록 배치하는 모든 경우의 수를 구하는 문제
후보 해의 수가 4,4,26165,368
하지만 가능한 수는 92회
해결 방법
- 4Queens 문제로 축소해서 생각해보기 → 같은행에 두는것 배제하고
- 모든 후보를 검사? → no!
백트레킹 기법
- 어떤 노드의 유망성을 점건한 후에 유망하지 않다고 결정되면 그 노드의 부모로 되돌아가기(backtracking)다음 자식 노드로 간다.
유망(promising)하다
- 어떤 노드를 방문 하였을때 그 노드를 포함한 경로가 해답이 될 수 있으면 유망하다고 한다.
- 가지치기
- 유망하지 않은 노드가 포함되는 경로는 더이상 고려하지 않는다.

백트래킹과 완전탐색(DFS)와의 차이
어떤 노드에서 출발하는 경로가 해결책으로 이어질것 같지 않으면 더 이상 그 경로를 따라가지 않음으로서 시도의 횟수를 줄임(pruning 가지치기)
완전 탐색이 모든 경로를 추적하는데 비해 백 트래킹은 불필요한 경로를 조기 차단한다.
완전 탐색을 가하기에는 경우의 수가 너무나 많다.
(예를 들어 , N! 가지의 경우의 수를 가진 문제에 대해 완전 탐색을 가하면 당연히 처리 불가능한문제)
백트래킹 알고리즘을 적용하면 일반적으로 경우의 수가 줄어들지만 이역시 최악의 경우에는 여전히 지수함수시간을 요하므로 처리 불가능할 수 있다.

백트래킹
상태공간 트리(가능한 첫번쨰 해를 만날 때까지의 경우로 가정)
같은 행에 퀸을 두지 않는 방식의 깊이 우선 탐색(DFS) vs 백트래킹
같은 행에 퀸을 두지 않는 방식의 깊이 우선 탐색
- 155노드 탐색 필요

부분 집합의 합 문제

문제 1. 부분집합의 합을 구해라

→그동안 완전 탐색으로 해결 했다. → 모든 부분집합을 생성한 후에 부분집합의 합을 계산했다.

문제 2.

유한개의 자연수(한정조건: 0,음수x)로 이루어진 집합이 잇을떄, 이 집합의 부분집합중에서 그 집합의 원소를 모두 더한값이 21되는 경우가 몇번인지 알아내는 문제

→ 원래 완전 탐색에서는 모두 다 더한뒤에 합을 계산 했다면

→ 백트레킹에서는

실습예제

파이프를 놓는 순서 ?

첫파이프를 놓는 위치에 따라 두,세번째 파이프 위치 영향받음 → 가장 윗행에서 시작해야한다!
수행횟수

한행 천열시도 3^c*R중간 건물, 기존파이프라인 시간 줄여주기는함)
가지치기!
1. 파이프놓기에 성공하면 처음으로(시작열) 계속리턴
2. 이전파이프놓기에 실패한 흔적 남겨둔다 → 또 들어가서 탐색 하지 앟는다.

전재우

코린이

이전 포스트

개인공부_4주차

다음 포스트

공부복습_5주차

2021년 02월 21일

SSAFY_4주차 리뷰

힙(heap)

삭제

우선순위 큐

java.utill.priorityQueue()

java.utill.priorityQueue(Comparator comparator)→비교 도우미

Comparable

compareTo( ) 메소드에서

Comparator

우선 순위를 처리하는 세가지 방법

완전 탐색(Exhaustive Search)

완전 탐색

순열(permutation)

nextPermutation

NextPermutation 을 이용한조합

NextPermutation을 이용한 부분집합 생성

탐욕(greedy) 알고리즘

배낭 짐싸기(Knapsack)

Knapsack 문제유형

0-1 Knapsack에 대한 완전 검색 방법

Fractional Knapsack에 대한 GREEDY한 방법

MeetingRoom greedy한 해결

분할 정복

분할정복 기법

이진 탐색

백트래킹

당첨 리프 노드 찾기

8-Queens 문제

백트래킹과 완전탐색(DFS)와의 차이

백트래킹

부분 집합의 합 문제

실습예제

개인공부_4주차

공부리뷰_6주차

0개의 댓글