🌈 너비 우선 탐색(BFS) & 깊이 우선 탐색(DFS)
🔥 그래프(graph)란?
🔥 그래프(graph)와 트리(tree)의 차이
🔥 그래프(graph) 표현
🔥 너비 우선 탐색(BFS)
🔥 깊이 우선 탐색(DFS)
🔥 BFS(Breadth-First Search) 예제
🔥 DFS(Depth-First Search) 예제
1. 그래프란?
- 그래프는 현상이나 사물을 정점(Vertex) 또는 노드(Node), 간선(Edge)로 표현하기 위해 사용
- 노드(Node) : 위치를 말함, 정점(Vertex)라고도 함
- 간선(Edge) : 위치 간의 관계를 표시한 선으로 노드를 연결한 선을 뜻함(Link 또는 Branch라고도 함)
- 인접 정점(Adjacent Vertext) : 간선으로 직접 연결된 Vertex(또는 Node)
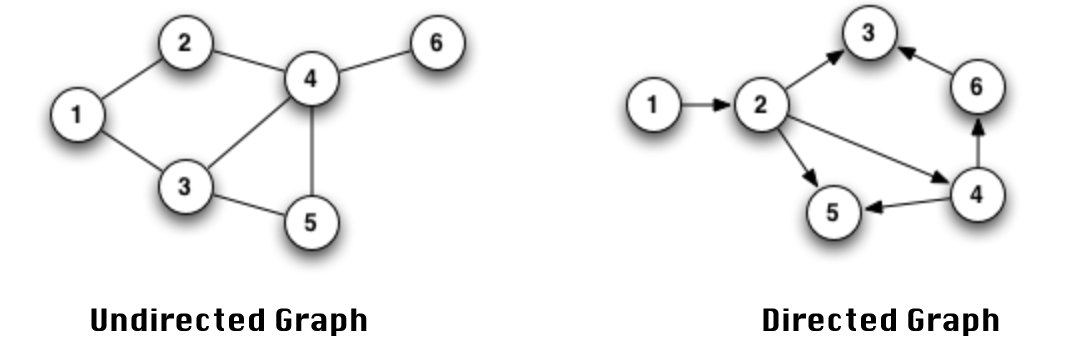
1) 무방향 그래프(undirected graph)
- 방향이 없는 그래프로 간선을 통해 노드는 양방향으로 갈 수 있음
- 보통 노드 A,B가 연결되어 있을 경우 (A,B) 또는 (B,A)로 표기
2) 방향 그래프(directed graph)
- 간선에 방향이 있는 그래프로 방향이 가르키는 곳으로만 갈 수 있음
- 노드 A->B로 연결되어 있을 경우 <A,B> 표기
- 노드 B->A로 연결되어 있을 경우 <B,A> 표기
3) 가중치 그래프(weighted graph) 또는 네트워크
- 간선에 비용 또는 가중치가 할당된 그래프
4) 싸이클(cycle)
- 단순 경로의 시작 노드와 종료 노드가 동일한 경우
5) 비순환 그래프(acyclic graph)
- 싸이클이 없는 그래프
6) 완전 그래프(complete graph)
- 그래프의 모든 노드가 서로 연결되어 있는 그래프
2. 그래프(graph)와 트리(tree)의 차이
- 그래프는 노드와 노드를 연결하는 간선으로 표현되는 자료구조이며, 트리는 그래프의 한 종류로서 방향성이 있는 비순환 그래프임
- 그래프는 방향 그래프, 무향방 그래프 모두 존재하지만, 트리는 방향 그래프만 존재
- 그래프는 싸이클이 가능(순환 및 비순환 모두 존재)하고, 트리는 비순환 그래프로 사이클이 존재하지 않음
- 그래프는 Root Node가 불필요하지만, 트리는 Root Node가 필요
- 그래프는 부모 자식 개념이 불필요하지만, 트리는 부모 자식 관계가 반드시 존재
3. 그래프(graph) 표현
- python에서 제공하는 딕셔너리와 리스트 자료 구조를 활용해서 그래프를 표현할 수 있음
- 각 Node를 Key로 한 뒤, 해당 Node에 연결된 Node들을 리스트 만들어 Value로 추가
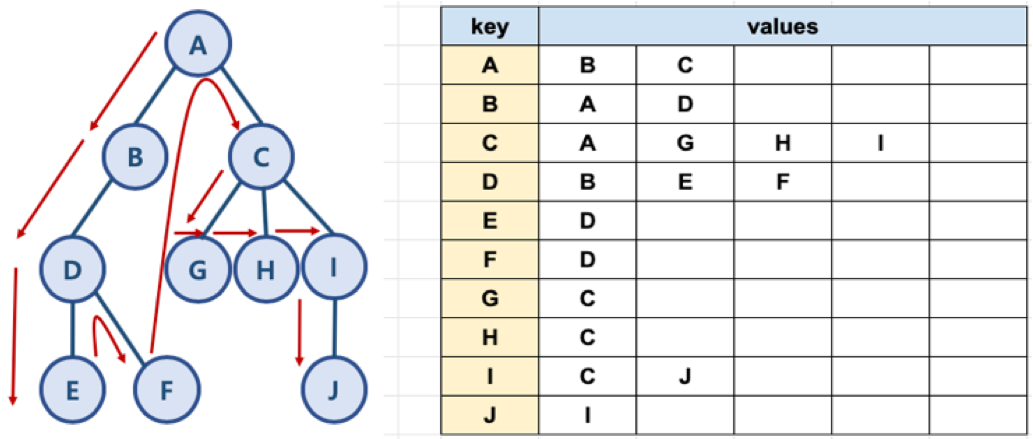
graph = dict() graph['A'] = ['B', 'C'] graph['B'] = ['A', 'D'] graph['C'] = ['A', 'G', 'H', 'I'] graph['D'] = ['B', 'E', 'F'] graph['E'] = ['D'] graph['F'] = ['D'] graph['G'] = ['C'] graph['H'] = ['C'] graph['I'] = ['C', 'J'] graph['J'] = ['I'] print(graph) """ { 'A': ['B', 'C'], 'B': ['A', 'D'], 'C': ['A', 'G', 'H', 'I'], 'D': ['B', 'E', 'F'], 'E': ['D'], 'F': ['D'], 'G': ['C'], 'H': ['C'], 'I': ['C', 'J'], 'J': ['I'] } """
4. 너비 우선 탐색(BFS)
- 너비 우선 탐색은 갈림길 마다 갈 수 있는 곳의 순서를 매긴 뒤, 순서가 매겨진 순으로 순차적으로 탐색(한 단계씩 내려가면서, 해당 Node와 같은 레벨에 있는 형제 노드를 먼저 탐색)
- 이에 너비 우선 탐색은 2개의 queue가 필요
- need_visit : 방문 예정(순서가 매겨진)인 방문 대기 queue
- visited : 이미 방문 한(순차적으로 방문한) 방문 완료 queue
- 너비 우선 탐색은 queue를 이용해 구현하고, 갈 수 있는 곳을 방문 대기 queue에 넣은 후 queue의 앞에서부터 하나씩 빼서 탐색하는 방식임
- 방문 대기 queue에서 앞에서부터 하나씩 빼서 이미 방문하였다면 스킵하고, 방문하지 않았다면 방문 리스트에 추가한 뒤, 추가된 Node에서 갈 수 있는 Node를 queue 뒤편에 줄을 세움
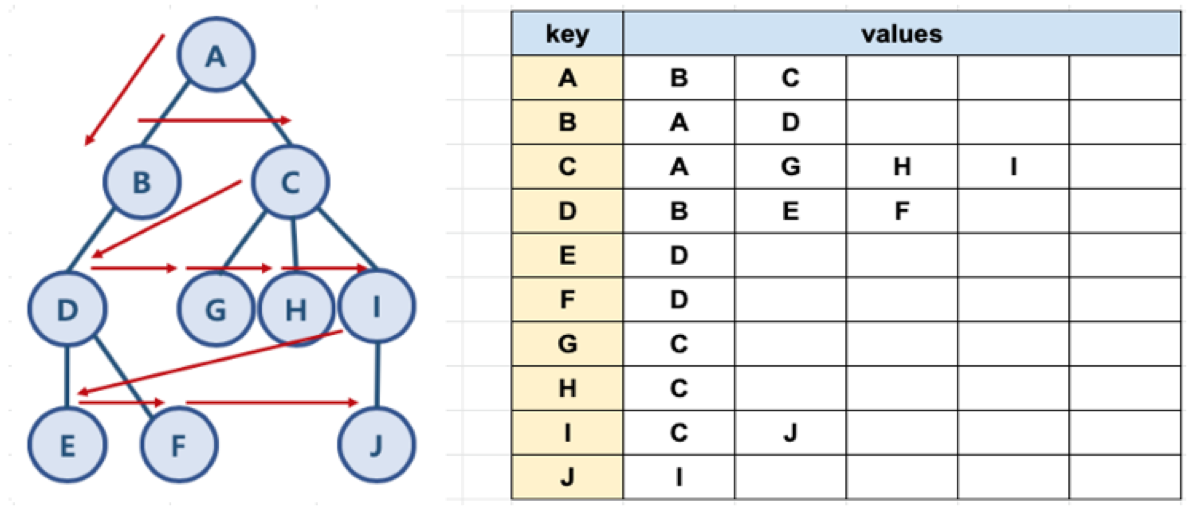
# BFS 구현 ## graph 표현 graph = dict() graph['A'] = ['B', 'C'] graph['B'] = ['A', 'D'] graph['C'] = ['A', 'G', 'H', 'I'] graph['D'] = ['B', 'E', 'F'] graph['E'] = ['D'] graph['F'] = ['D'] graph['G'] = ['C'] graph['H'] = ['C'] graph['I'] = ['C', 'J'] graph['J'] = ['I'] ## BFS def bfs(graph, start_node): # 그래프와 시작 Node를 넣음 visited = list() # 방문 완료한 queue 생성 need_visit = list() # 방문 대기열 queue 생성 # start_node를 맨 처음 방문 대기열에 추가 need_visit.append(start_node) # 방문 대기열이 존재하지 않을 때 까지 반복 while need_visit: node = need_visit.pop(0) # 대기열에서 맨 처음 요소를 제거하고 node에 담음 if node not in visited: # node가 방문 완료 queue에 있는지 확인 visited.append(node) # 없으면 방문 완료 queue에 추가 need_visit.extend(graph[node]) # node와 연결된 Node들을 대기열에 추가 return visited # BFS TEST print(bfs(graph, 'A')) # ['A', 'B', 'C', 'D', 'G', 'H', 'I', 'E', 'F', 'J']
- BFS에서 Node의 수를 V, 간선의 수를 E라고 할 때, 시간 복잡도는 O(V+E)
- BFS는 queue를 이용해 구현하고, 갈 수 있는 곳을 전부 queue에 넣은 후 queue의 앞에서부터 하나씩 빼서 탐색하는 방식임
- 즉, 갈림길 마다 기준에 맞추어 경로를 queue에 넣은 후, 먼저 추가된 경로(우선 순위 높은 경로)를 차례대로 탐색
1) 정수삼각형 BFS로 풀기
- 맨 위에서 시작해서 아래에 있는 수를 하나 선택해서 내려올 때, 선택된 수의 합 중 최대값을 출력
# BFS로 풀기 # 삼각형 입력 """ 5 <- 높이 입력 삼각형 시작 지점(0,0) 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 """ import sys from queue import deque # push def queue_push(q, value): q.append(value) # popleft def queue_pop(q): return q.popleft() # 삼각형 입력 n = int(sys.stdin.readline()) l = [] for i in range(n): ll = list(map(int, sys.stdin.readline().split())) l.append(ll) # print(l) # [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] # BFS 구현 q = deque() ans = -1 queue_push(q, [0,0,0]) # y=0, x=0, s=0 while len(q) != 0: front = queue_pop(q) # 0, 0 if front[0] == n and ans < front[2]: ans = front[2] # print(front) # 경로 if front[0] < n: left = [front[0] + 1, front[1], front[2] + l[front[0]][front[1]]] # 1, 0 right = [front[0] + 1, front[1] + 1, front[2] + l[front[0]][front[1]]] # 1, 1 queue_push(q, left) queue_push(q, right) # 호출 print(ans)
5. 깊이 우선 탐색(DFS)
- 깊이 우선 탐색은 일단 탐색할 수 있을 때까지 깊게 탐색하고, 더이상 탐색할 대상이 없으면 갈림길이 존재하는 지나친 최근 노드로 돌아와 아래로 탐색하는 방식임(정점의 자식들을 먼저 탐색)
- 이에 깊이 우선 탐색은 1개의 stack과 1개의 queue가 필요
- need_visit : 방문 예정(순서가 매겨진)인 방문 대기 stack
- visitied : 이미 방문 한(순차적으로 방문한) 방문 완료 queue
- DFS는 start_node 부터 시작하여, visited에 없으면 뒤에 추가해주고 동시에 해당 Node에서 갈 수 있는 연결된 Node를 방문 예정 stack에 추가함
- 다음으로 방문 예정 stack에 맨 뒤에 요소를 꺼내 visited에 없으면 추가하고 있으면 다음 맨 뒤에 요소를 visited에 있는 확인하는 패턴이 반복
- BFS는 방문 대기 queue에 추가하고 먼저 추가된 Node부터 꺼내어 이미 방문하였는지 확인하는데 반해, DFS는 방문 대기 stack에 추가하고 가장 나중에 추가된 Node부터 꺼내어 이미 방문하였는지 확인하는 차이가 있음
# DFS 구현 # graph 표현 graph = dict() graph['A'] = ['B', 'C'] graph['B'] = ['A', 'D'] graph['C'] = ['A', 'G', 'H', 'I'] graph['D'] = ['B', 'E', 'F'] graph['E'] = ['D'] graph['F'] = ['D'] graph['G'] = ['C'] graph['H'] = ['C'] graph['I'] = ['C', 'J'] graph['J'] = ['I'] # DFS def dfs(graph, start_node): visited = list() # 방문 완료한 queue 생성 need_visit = list() # 방문 대기열 stack 생성 # start_node를 맨 처음 방문 대기열에 추가 need_visit.append(start_node) # 방문 대기열이 존재하지 않을 때 까지 반복 while need_visit: node = need_visit.pop() if node not in visited: visited.append(node) need_visit.extend(graph[node]) return visited # DFS TEST # 왼쪽 측면이든, 오른쪽 측면이든 깊이를 기준으로 탐색하면 DFS print(dfs(graph, 'A')) # ['A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E']
- DFS에서 Node의 수를 V, 간선의 수를 E라고 할 때, 시간 복잡도는 O(V+E)
- DFS는 깊이 우선 탐색이라고도 부르며, 일단 탐색할 수 있을 때까지 깊게 탐색하고, 더이상 탐색할 대상이 없으면 갈림길이 존재하는 지나친 노드로 되돌아가 계속 깊이를 기준으로 탐색하는 방식임
- DFS는 재귀함수 또는 Stack을 이용해 구현하는데 보통 재귀함수로 구현하는게 더욱 간편함
1) 정수삼각형 DFS로 풀기
- 맨 위에서 시작해서 아래에 있는 수를 하나 선택해서 내려올 때, 선택된 수의 합 중 최대값을 출력
# DFS로 풀기 # 삼각형 입력 """ 5 <- 높이 입력 삼각형 시작 지점(0,0) 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5 """ import sys ans = -1 # dfs 구현 def dfs(l, y, x, s): global ans if y == len(l): if ans < s: ans = s return # print(y,x,ans) # 탐색하는 과정 dfs(l, y+1, x, s+l[y][x]) # 아래로 이동 dfs(l, y+1, x+1, s+l[y][x]) # 대각선 오른쪽으로 이동 # 삼각형 입력 n = int(sys.stdin.readline()) l = [] for i in range(n): ll = list(map(int, sys.stdin.readline().split())) l.append(ll) # print(l) # [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] # 호출 dfs(l,0,0,0) # 삼각형(l)에서 0,0부터 시작 / s=0 부터 print(ans)
6. BFS(Breadth-First Search) 예제
1) BOJ 1012 - 유기농 배추
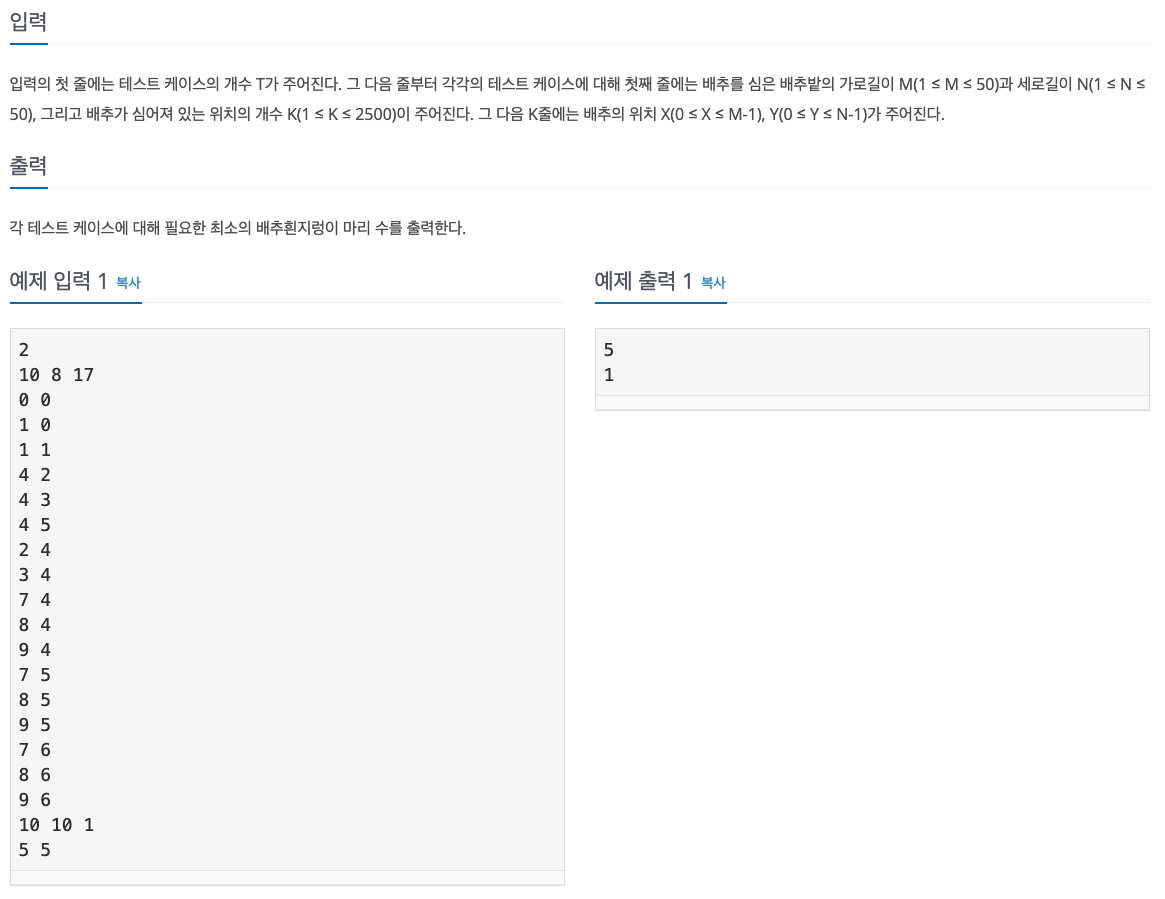
# BOJ 1012(유기농 배추) """ 2 <= 테스트 케이스 10 8 17 <= 첫번째 배추밭(m,n,k) 0 0 1 0 1 1 4 2 4 3 4 5 2 4 3 4 7 4 8 4 9 4 7 5 8 5 9 5 7 6 8 6 9 6 10 10 1 <= 두번째 배추밭(m,n,k) 5 5 """ import sys def dfs(l,y,x): l[y][x] = 0 dy = [-1, 0, 1, 0] dx = [0, 1, 0, -1] # i => 0일 때는 top, 1일 때는 right, 2일 때는 bottom, 3일 때는 left for i in range(4): ny = y + dy[i] nx = x + dx[i] if ny < 0 or ny >= len(l) or nx < 0 or nx >= len(l[0]): continue if l[ny][nx] != 1: continue dfs(l, ny, nx) T = int(sys.stdin.readline()) for test_case in range(T): M, N, K = list(map(int, sys.stdin.readline().split())) l = [[0 for i in range(M)] for j in range(N)] for i in range(K): x, y = list(map(int, sys.stdin.readline().split())) l[y][x] = 1 cnt = 0 for i in range(N): for j in range(M): if l[i][j] == 1: cnt += 1 dfs(l, i, j) print(cnt)
7. DFS(Depth-First Search) 예제
1) BOJ 1012 - 유기농 배추
# BOJ 1012(유기농 배추) """ 2 10 8 17 0 0 1 0 1 1 4 2 4 3 4 5 2 4 3 4 7 4 8 4 9 4 7 5 8 5 9 5 7 6 8 6 9 6 10 10 1 5 5 """ import sys # queue_push from queue import deque def queue_push(q, value): q.append(value) # queue_pop def queue_pop(q): front = q.popleft() return front # bfs def bfs(l,y,x): q = deque() queue_push(q, [y, x]) while len(q) != 0: # i => 0일 때는 top, 1일 때는 right, 2일 때는 bottom, 3일 때는 left front = queue_pop(q) l[front[0]][front[1]] = 0 dy = [-1, 0, 1, 0] dx = [0, 1, 0, -1] for i in range(4): ny = front[0] + dy[i] nx = front[1] + dx[i] if ny < 0 or ny >= len(l) or nx < 0 or nx >= len(l[0]): continue if l[ny][nx] != 1: continue queue_push(q, [ny, nx]) T = int(sys.stdin.readline()) for test_case in range(T): M, N, K = list(map(int, sys.stdin.readline().split())) l = [[0 for i in range(M)] for j in range(N)] for i in range(K): x, y = list(map(int, sys.stdin.readline().split())) l[y][x] = 1 cnt = 0 for i in range(N): for j in range(M): if l[i][j] == 1: cnt += 1 bfs(l, i, j) print(cnt)
- DFS는 재귀함수 혹은 Stack으로 구현 가능하나, 일반적으로 재귀함수를 사용하고 최단경로를 구하는데 효과적임
- BFS는 Queue를 이용하여 구현하고, 일반적인 전탐색에 주로 활용
Keep Going, Keep Coding!