들어가며

해시 테이블은 우리가 가장 자주 사용하는 자료구조 중 하나입니다.
O(1)의 빠른 탐색과 삽입 덕분에, Python의 dict, Java의 HashMap, C++의 unordered_map 등 다양한 언어에서 해시테이블은 서비스 구현의 핵심을 맡고 있습니다.

그런데 최근, Rutgers 대학의 학부생 Andrew Krapivin은 기존 해시 테이블의 성능 한계를 완전히 깨는 새로운 구조를 제안하며 큰 주목을 받았습니다. Krapivin은 1985년 Andrew Yao 교수가 제시한 40년 된 추측이 틀림을 증명했으며, 실제로 해시 테이블에서 더 빠른 탐색과 삽입이 가능함을 수학적으로 증명했습니다.

이 글에서는 Krapivin의 연구를 쉽게 풀어 설명하고, 어떻게 해시 테이블의 근본적 성능이 개선될 수 있었는지 알아보겠습니다.

Hash Table

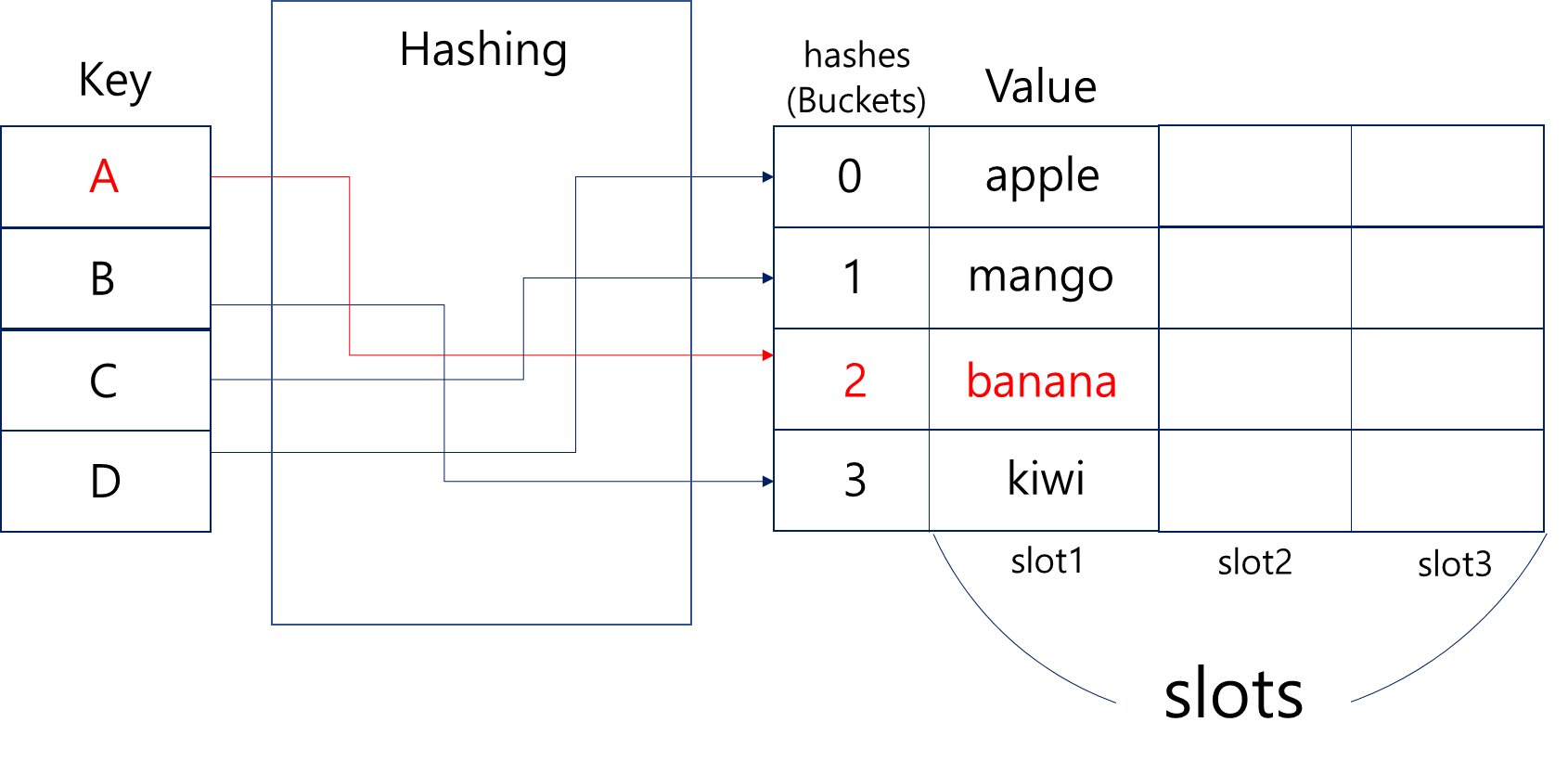
해시 테이블은 키(key)를 해시 함수(hash function)에 넣어 계산된 인덱스를 통해 값을 저장하거나 조회하는 자료구조입니다.
해시 함수는 임의 길이의 입력값을 받아 고정된 길이의 출력값을 내는 함수인데요. Key 값에 해당하는 Value를 자체적으로 가지기 때문에, value를 index로 구분해서 저장하기 때문에 해당 Key를 입력하면 그에 해당하는 위치에서 바로 꺼내오는 원리입니다.
해시함수는 완벽하게 value의 독립성을 보장하기엔 한계가 있기 때문에, 당연히 각각의 Key들이 최대한 서로 다른 Value를 가지는 해시함수를 선택하는 것이 중요합니다.
서로 다른 key가 같은 value를 가지는 경우, 우리는 이것을 해시 충돌(Hash Collision)이라고 합니다.

Collision

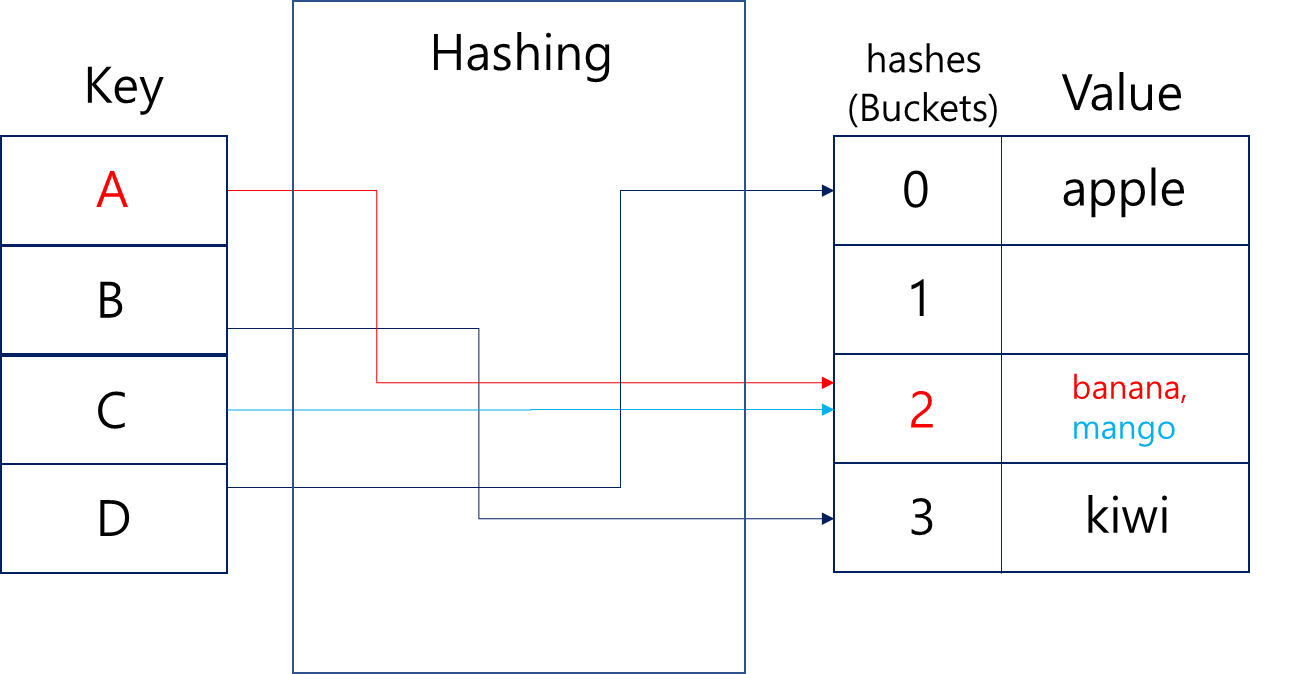
위 그림을 보시면 알 수 있듯, B와 D는 각각 해시함수의 결과값이 3과 0이 나와서 kiwi와 apple이라는 값을 잘 저장한 것을 볼 수 있습니다. 하지만 A와 C는 모두 2의 결과값을 가지게 되어 banana와 mango의 밸류가 충돌하게 되었네요.

완벽한 해시함수란 없기 때문에 이런 경우에 대한 well-known 솔루션이 존재합니다.

Chaining

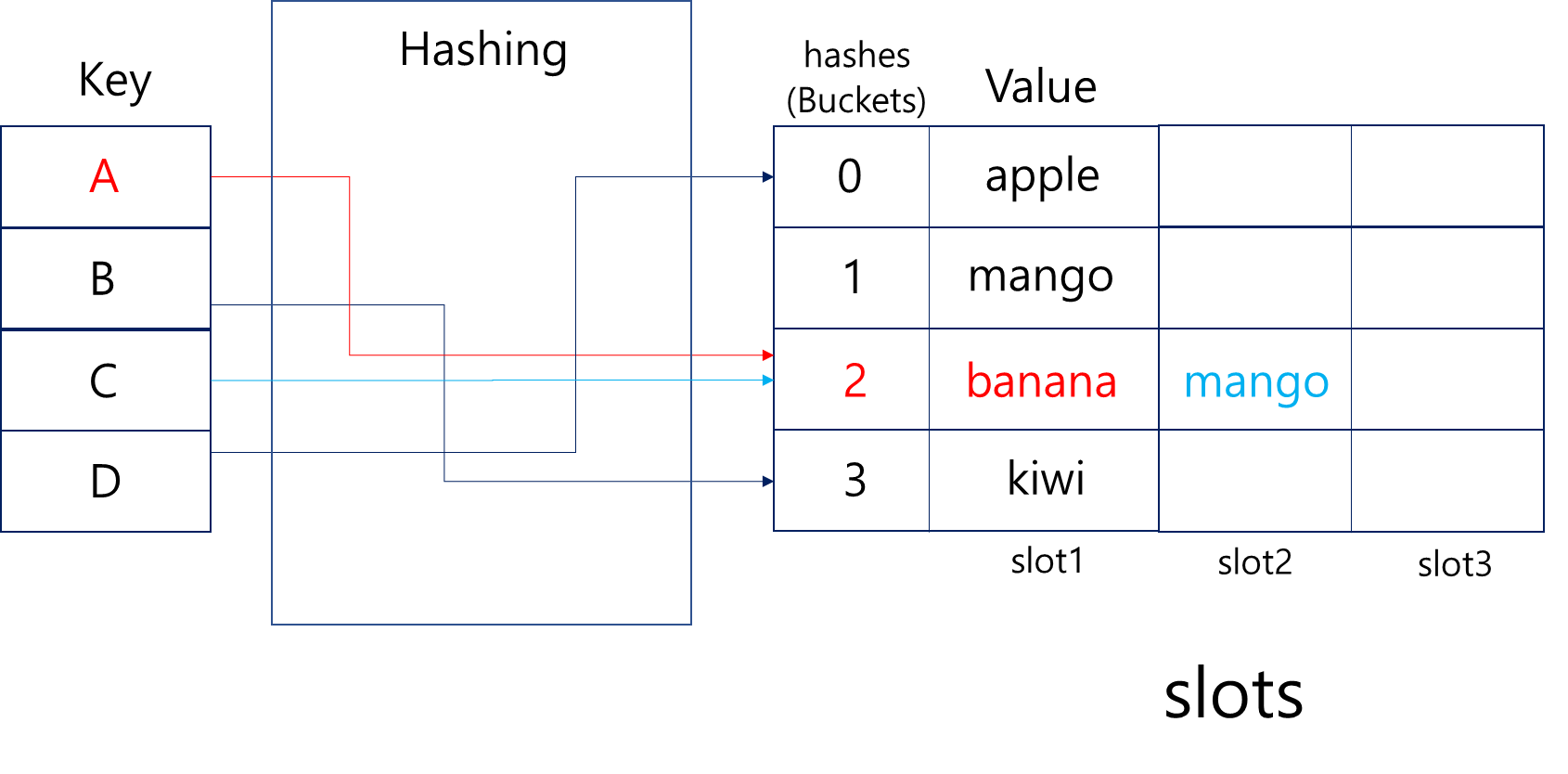
해시 충돌이 발생할 경우, 해시테이블은 Chaining, Open addressing 등으로 충돌을 회피하는데요.
먼저 Chaning은 value에 대한 추가적인 공간(slot)을 만들어 value가 담기는 버킷의 다음 칸에 연이어서 넣어주는 방식입니다.

이 경우, 해시 충돌이 발생할 때 기존의 버킷을 활용할 수 있지만 해시테이블이 가득 찰수록 성능은 선형적으로 떨어지게 됩니다.
예를 들어 100가지 과일을 해시테이블에 추가했는데 하필 hash 결과값이 모두 2로 통일되는 경우가 있습니다. 마지막(100번째)에 넣은 과일을 찾을 때는 최소한 100개의 슬롯을 O(n)으로 탐색해야겠죠?

Open Addressing

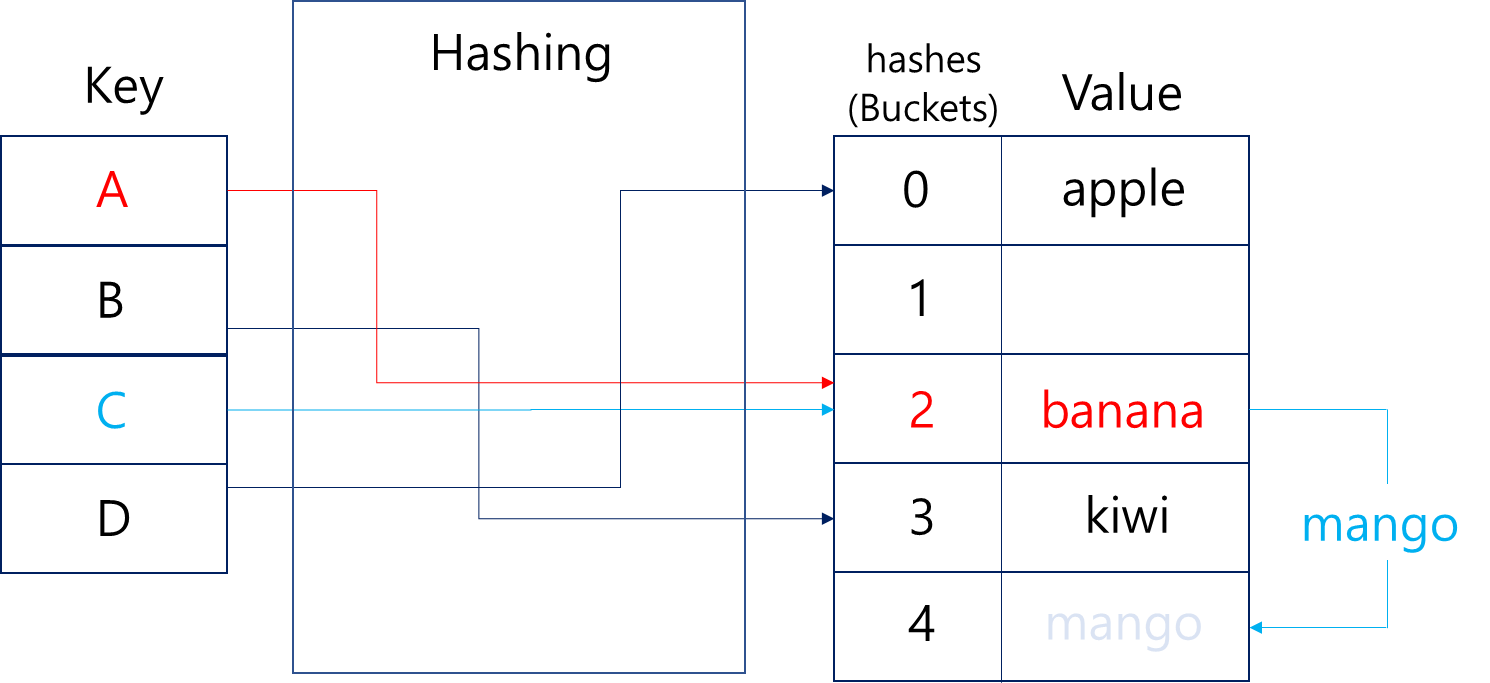
Open addressing은 Chaining과 달리, 충돌 발생시 같은 버킷에 넣지 않고 다른 버킷을 찾는 방법입니다.
이 때 다른 빈 버킷을 찾는 과정을 탐사(probing)이라고 하는데요. 선형으로 탐사하여 빈 버킷을 찾을 수도 있고, 지수적으로 2칸, 4칸, 8칸, ... 등 간격을 늘려가며 빈 버킷을 찾을 수도 있습니다.

위의 사진에서는 banana가 먼저 2번 자리를 차지하고 있었기 때문에, mango가 4번 자리로 밀려난 것이 예시가 될 수 있겠네요. 다만 여전히 C를 해시함수에 넣으면 2가 나오기 때문에, mango를 찾으려면 항상 2번을 확인하는 과정을 거쳐야 합니다.

충돌이 발생했을 때, 데이터를 넣기 위해 다음 빈 슬롯을 찾아 나가는 과정에서 데이터들이 연속적으로 몰리게 되는 현상을 클러스터링(Clustering)이라고 하는데요.

예를 들어, 선형 탐사(Linear Probing)에서 충돌이 계속 발생하면 클러스터링 현상이 생기고, 결국 특정 위치에 연속적으로 요소가 몰리는 바람에 탐색, 삽입 모두 O(n)까지 떨어질 수 있습니다.

테이블 크기: 10
해시 함수: key % 10

삽입 순서: 10, 20, 30

• 10 % 10 = 0 → [0] 에 저장
• 20 % 10 = 0 → [0] 충돌 → [1] 에 저장
• 30 % 10 = 0 → [0], [1] 충돌 → [2] 에 저장

→ 테이블 크기는 10이지만 [0], [1], [2]에 데이터가 몰려 있는 상태가 됨

해시충돌을 회피하려는 2가지 방법은 충분히 효율적이나 최악의 경우 O(n)의 시간복잡도라는 것을 기억하시면 좋습니다.

Time Complexity

해시테이블은 충돌이 적은 좋은 해시함수로 구현될 경우, 평균적으로 삽입과 조회에 O(1)의 시간복잡도를 가집니다.
현대의 해시테이블은 쉽게 포화되지도 않고, 자료구조 중 매우 빠른 삽입과 조회를 보장하기 때문에 엔터프라이즈 레벨에서도 많은 사랑을 받는 자료구조입니다.

지금까지는 최악의 경우에 해시테이블 성능이 매우 떨어진다는 식으로 적은 것 같네요. 하지만 해시테이블은 최악의 경우에도 다른 탐색의 최악 경우와 비슷하게 O(n)으로 접근할 수 있기 때문에, 성능 하한은 비슷하지만 성능 상한이 매우 뛰어난 자료구조라고 할 수 있습니다.

Uniform Probing

현대 해시테이블은 해시충돌을 균일 탐사(Uniform Probing)로 해결합니다.
Uniform Probing은 해시 충돌이 발생했을 때, 고정된 간격 d만큼 떨어진 인덱스를 순서대로 탐색합니다.

탐색 순서는 아래와 같습니다.

h(k) → h(k) + d → h(k) + 2d → h(k) + 3d → ... (mod 테이블 크기)

이 간격 d는 일반적으로 테이블 크기와 서로소(coprime)인 값이어야 모든 슬롯을 순회할 수 있습니다.
해시 함수가 h(k) = k % 10일 때, 탐사 간격이 10과 서로소인 d=3이라면 다음과 같이 모든 슬롯을 순회하는 것을 알 수 있습니다.

• h(27) = 7
• 슬롯 7 비어 있으면 → 삽입
• 아니면 다음: 7 + 3 = 10 → 10 % 10 = 0
• 아니면 다음: 0 + 3 = 3, ...

탐색 순서: 7 → 0 → 3 → 6 → 9 → 2 → 5 → 8 → 1 → 4

중복없이 모든 슬롯을 순회하기 때문에, Chaining과 Open Addressing의 장점은 챙기면서 단점은 완화하는 방법임을 직관적으로 알 수 있습니다.

알파는 load factor 라고 부르는데요. 해시 테이블이 얼마나 가득 찼는지를 의미하는 지표입니다. 이미 알파가 0.6 이하(60%의 포화도)일 때 Uniform Probing이 Linear Probing 보다 뛰어남이 증명되어 있습니다.

이러한 Uniform Probing 방식을 전제로, Andrew Yao 교수는 1985년에 다음과 같은 주장을 했습니다.

"균일 탐사가 가능한 해시 테이블에서, 최악의 경우 삽입 시간은 테이블의 포화도(x)에 정비례한다."

이는 40년동안 정설로 굳어져왔고, 이를 논파하려 시도한 사람은 거의 없었습니다. 최악의 경우가 너무나도 직관적으로 명료했기 때문이 아닐까 싶네요.

Krapivin Hash Table

하지만 최근 루트거스 대학의 학부생 Andrew Krapivin가 40년간 자리잡아온 O(n)의 최악 시간복잡도를 O(log² x)으로 개선하는데 성공합니다.

Andrew Krapivin는 2021년 Tiny Pointer라는 논문을 처음 접했습니다. 처음엔 관심 없었지만 2년 뒤, 그 논문을 다시 읽으며 포인터를 더 작게 만드는 아이디어를 떠올렸고, 이 과정에서 새로운 해시테이블을 발명하게 되었습니다.

Tiny Pointers

일반적으로 포인터는 64비트(또는 32비트)를 사용해서 메모리 주소를 가리키는데요. Tiny Pointer는 전체 주소를 저장하는 게 아니라, 필요한 정보만을 인코딩해서 더 작은 비트 수로 메모리를 저장하는 방식입니다.

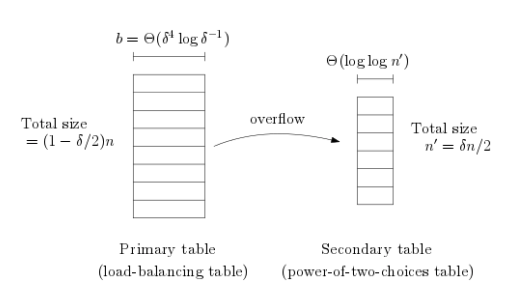
먼저 전체 메모리 공간을 블록으로 나눕니다. 이후 블록 ID + 오프셋으로 위치를 가리킨다면 포인터를 미니멀하게 구현 가능합니다.

우리가 교과서에서 220 페이지를 펴야할 때 하나하나 넘기며 펼 수도 있지만, 2단원 첫장(200p)의 위치를 안다면 그로부터 20 페이지만 더 넘기면 되는 원리와 똑같습니다.

Krapivin probing

Krapivin의 방법은 Uniform probing이 아닌 새로운 방식을 선택했습니다. 바로 non-greedy한 probing으로 넓게 흩어진 후보 위치를 검사하는 방식인데요. 보통 삽입 시 첫번째로 찾은 빈 슬롯 데이터에 데이터를 넣는 직관과는 다른 방식입니다.

해시 테이블이 x 만큼 가득 찼다고 가정한다면, 빈 슬롯을 찾기 위해 확률적으로 1/x의 확률로 한 칸이 비어있다고 봤을 때, 단순 랜덤 시도는 O(x) 만큼 필요합니다.

하지만 잘 설계된 탐색 순서로 공간 전체를 골고루 커버하면, 적은 횟수로도 빈 칸을 발견할 확률을 크게 높일 수 있으며, Krapivin이 제안한 방식은 log(x)만큼 넓게, log(x)번 정도 탐색하는 구조로 되어 있습니다.

때문에 탐색 과정에서 O(log² x)라는 최적 경계(lower bound)를 찾을 수 있습니다.

Krapivin probing 구현

전통적인 해시 테이블은 충돌이 발생했을 때 Greedy한 선형 탐색(Linear Probing)을 사용한다고 했습니다. 즉, 현재 인덱스에서 가능한 가장 가까운 슬롯부터 차례로 확인하면서, 빈 슬롯을 찾는 방식입니다. 이 방법은 간단하지만, 특정 위치에 데이터가 몰리는 클러스터링 문제(primary clustering) 를 유발하여 성능이 저하될 수 있다고도 알아봤었죠.

Krapivin은 그 반대 전략인 Non-Greedy한 방법으로 탐색을 수행합니다. 해시 충돌이 발생해도 무작정 가까운 곳을 탐색하지 않고, 오히려 계산된 규칙을 바탕으로 넓게 퍼진 후보 슬롯을 탐색합니다. 이 방식은 해시 테이블 전반에 데이터를 분산시켜 클러스터링을 줄이는 효과가 있습니다.

아래에서 기존의 Greedy 방식과 Krapivin의 방식을 비교해보겠습니다.
아직 구현 코드는 공개되지 않았지만, 논문을 참고하여 구조를 구성해보았습니다.

greedy(linear)

먼저 기존의 선형 탐사 기반 해시 테이블을 구현해보겠습니다.

class LinearProbingHashTable:
    def __init__(self, size):
        self.size = size
        self.table = [None] * size

    def _hash(self, key):
        return hash(key) % self.size

    def insert(self, key, value):
        idx = self._hash(key)
        original_idx = idx  # 무한 루프 방지를 위해 시작점 저장
        steps = 0

        # 충돌 발생 시, 다음 슬롯으로 1칸씩 이동하며 빈 칸 탐색
        while self.table[idx] is not None:
            idx = (idx + 1) % self.size
            steps += 1

            # 한 바퀴 돌면 테이블이 가득 찼다는 뜻
            if idx == original_idx:
                raise Exception("Hash table is full")

        self.table[idx] = (key, value)
        return steps  # 충돌 해결에 소요된 step 수 리턴

    def get(self, key):
        idx = self._hash(key)
        original_idx = idx

        # 같은 해시 인덱스를 공유하는 여러 요소들 중 키 일치 항목 탐색
        while self.table[idx] is not None:
            if self.table[idx][0] == key:
                return self.table[idx][1]

            idx = (idx + 1) % self.size

            # 순환 탐색 종료 조건: 원래 위치로 되돌아옴
            if idx == original_idx:
                break

        return None  # 탐색 실패

보시다시피 충돌이 발생할 때, 한 칸씩 뒤로 미루며 빈 버킷을 찾는 방식입니다. 매우 직관적이죠?

non-greedy(Krapivin)

class KrapivinProbingHashTable:
    def __init__(self, size):
        self.size = size
        self.table = [None] * size

    def _hash(self, key):
        return hash(key) % self.size

    def _probe_sequence(self, idx):
        # 비탐욕적 탐색: log x 만큼 거리를 두고 흩어진 후보군 생성
        max_probe = int(math.log2(self.size)) ** 2
        for i in range(1, max_probe + 1):
            yield (idx + i ** 2) % self.size  # 제곱거리만큼 뛰어넘음

    def insert(self, key, value):
        idx = self._hash(key)
        steps = 0

        if self.table[idx] is None:
            self.table[idx] = (key, value)
            return steps

        for next_idx in self._probe_sequence(idx):
            steps += 1
            if self.table[next_idx] is None:
                self.table[next_idx] = (key, value)
                return steps

        raise Exception("Hash table is full")

    def get(self, key):
        idx = self._hash(key)

        if self.table[idx] and self.table[idx][0] == key:
            return self.table[idx][1]

        for next_idx in self._probe_sequence(idx):
            if self.table[next_idx] and self.table[next_idx][0] == key:
                return self.table[next_idx][1]

        return None

반면 Krapivin의 방식은 크게 2가지 step으로 나뉩니다.

1. O(log² n)의 시간복잡도로 탐색 후보를 설정하는 _probe_sequence

• _probe_sequence는 기본 인덱스에서 시작해 거리를 제곱 단위로 증가시키며 슬롯을 탐색합니다.
• 예를 들어 i=1부터 시작해 1², 2², 3², ...만큼 떨어진 위치를 순회하며 후보 인덱스를 반환합니다.
• 최대 시도 횟수는 log²(n) 회로 제한하여 효율성을 유지합니다.

2. O(log n)의 시간복잡도로 실제 탐색을 수행하고 값에 접근하는 insert, get

• insert: 먼저 기본 해시 위치를 확인하고, 충돌이 발생하면 _probe_sequence에서 나온 인덱스 중 비어 있는 곳에 삽입합니다.
• get: 마찬가지로 충돌을 고려해 _probe_sequence로 값을 탐색합니다.

이렇게 2가지 step이 합연산으로 수행되어, O(log² n) + O(log n) ≈ O(log² n)의 시간복잡도를 가지는 것을 확인할 수 있습니다.

Result

def test_with_load_factor(table_class, table_size, load_factor):
    num_elements = int(table_size * load_factor)
    ht = table_class(table_size)
    total_steps = 0

    try:
        for i in range(num_elements):
            steps = ht.insert(f"key{i}", i)
            total_steps += steps
        avg_steps = total_steps / num_elements
        print(f"{table_class.__name__:<25} {table_size:>12,d}       {load_factor:>5.1%}       {avg_steps:>6.2f}")
    except Exception as e:
        print(f"{table_class.__name__:<25} {table_size:>12,d}       {load_factor:>5.1%}       {'실패':>4}")

def run_comparison():
    sizes = [1000, 10000, 100000]
    load_factors = [0.5, 0.9, 0.99]
    
    for size in sizes:
        print(f"\n[테이블 크기: {size:,}]")
        print("-" * 64)
        print(f"{'해시테이블 종류':<20} {'테이블 크기':>5}    {'적재율':>5}    {'평균 스텝'}")
        print("-" * 64)
        for load_factor in load_factors:
            test_with_load_factor(LinearProbingHashTable, size, load_factor)
            test_with_load_factor(KrapivinProbingHashTable, size, load_factor)
            if load_factor != load_factors[-1]:
                print()
        print("-" * 64, "\n")

run_comparison()

테스트는 table_size와, 전체 테이블 사이즈 중 얼마나 포화되었는지 비중을 의미하는 load_factor를 이용하여 step 수를 비교하도록 설계했습니다.

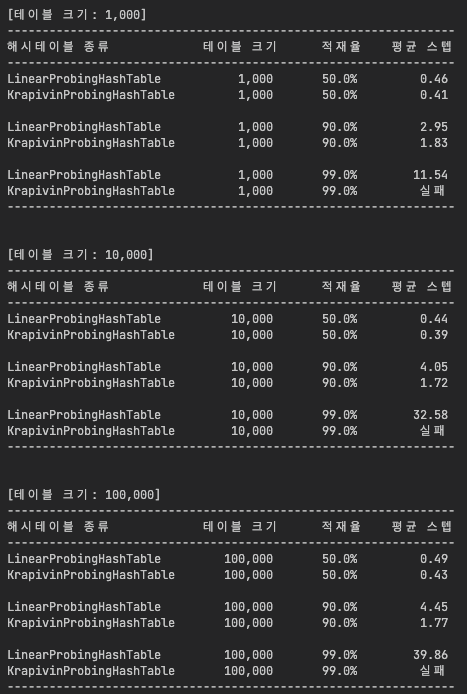
먼저 적재율 50%의 경우, 두 방식 모두 평균 스텝 수 1 미만으로 매우 빠르게 접근이 완료됨을 확인할 수 있습니다. 이 구간에서는 충돌이 거의 없기 때문에, 구조 차이에 따른 성능 차이가 미미함을 알 수 있습니다.

반면 적재율 90%의 경우는 아래와 같은 유의미한 차이가 발생합니다.

• LinearProbingHashTable: 평균 스텝이 4~5배 증가, 군집화(clustering) 발생
• KrapvinProbingHashTable: 증가폭이 완만하고, log²(x) 성장 경향을 보임

→ 공간 활용이 높아도 충돌 분산이 잘 이뤄짐

하지만 적재율 99%에서는 또 재미있는 결과를 확인할 수 있습니다.

• LinearProbingHashTable: 평균 스텝수가 10~40 수준으로 급등
• KrapvinProbingHashTable: 접근 실패 발생

→ log(x) 회수의 탐색 범위 내에서 빈 슬롯을 찾지 못해 예외 발생

이렇듯 적재율이 매우 큰 경우에 krapvin 방식은 탐색에 큰 단점이 있음을 알 수 있습니다.
물론 제가 탐색 횟수를 임의로 제한하도록 구현했기 때문이지만, 적재율이 과도한 상태에서 krapvin 방식은 탐색 범위 파악에서 한계가 있음이 분명합니다.
Linear한 경우도 10만건에 대해 평균 40 스텝만으로 찾아내는 걸 보면, 적재율이 과도한 상태라도 Linear도 충분히 효율적임을 알 수 있습니다.

마치며

해시 테이블은 CS 분야에서 가장 오래되고 널리 활용되는 자료구조 중 하나입니다. 그만큼 이론적으로도 철저히 분석되었고, 성능의 한계 또한 오랜 시간 정립되어 왔죠. 많은 엔지니어와 연구자들은 해시 테이블의 개선 여지에 대해 고민조차 안 해보았을지 모릅니다.

학부생이 이러한 통념을 뒤집은 것은 참 고무적이고 놀라운 일인 것 같습니다. 이번 포스팅은 동작 원리에 대한 깊은 이해가 얼마나 중요한지 되새기는, 저에게는 매우 인상깊은 사례가 될 것 같습니다. Krapivin과 같이 익숙한 것들을 의심하고 탐구하는 과학자의 자세가 저와 여러분의 엔지니어 커리어에 깃들기를 바랍니다.

References

• CS - 해시테이블, 해시함수 정리(Chaining, Open addressing)
  
• Tiny Pointers - arxiv
• Undergraduate Upends a 40-Year-Old Data Science Conjecture
• Optimal Bounds for Open Addressing Without Reordering - arxiv