
걱정을 해서 걱정이 사라지면 걱정이 없겠다.
라는 생각을 지울 수 없는 나날이다ㅋㅋ
회사 괜히 나왔나 라는 생각이 자주 드는 요즘이라 공부가 손에 잘 안잡힌다.
그래서 오랜만에 알고리즘 책을 다시 펴서 복습했다.
이번에 복습한 내용은 병합정렬 Merge Sort다.
Python이나 Javascript처럼 리스트를 쉽게 slice할 수 있다면 쉽게 재귀로 쉽게 구현할 수 있을거 같은데, C로 구현하려다 보니 손이 꽤 가는 느낌을 받았다.
병합이란?
병합이란 여러개의 이미 배열된 자료를 합치는 방법을 의미한다. 근데 그냥 합치는게 아니라 정렬을 해서 합친다.
예를 들어서 ["A", "E", "L", "N", "R"] 이 차례대로 정렬되어 있는 A라는 배열과, ["O", "R", "S", "T"] 라는 정렬되어 있는 B라는 배열을 병합해서 새로운 C라는 배열을 만들면 아래와 같다.
["A", "E", "L", "N", "O", "R", "R", "S", "T"]
병합하는 방법은 간단한데, 먼저 A배열의 A와 B배열의 O를 비교한다. 그러면 A가 O보다 더 작은 값이기에 C배열에 먼저 집어넣는다.
다음은 A배열의 E와 B배열의 O를 비교하는데, 마찬가지로 A배열의 E가 B배열의 O보다 더 작은 값이기에 C배열에 먼저 집어넣는다.
이런 과정을 반복하는게 병합이고, 병합의 끝은 두 배열에 모두 자료가 없는 경우다.
이렇게 병합은 두개의 배열에서 차례대로 꺼내지는 최소값들을 비교해서 작은 쪽의 값을 선택하는 방법으로 이루어지는데, 이때 반드시 한쪽의 배열이 먼저 소진되는 경우가 발생하기때문에 대비를 해야한다.
A배열의 자료의 갯수 an, 그리고 B배열의 자료의 갯수 bn인 배열을 병합해 C배열을 만든다라고 가정하자.
i = j = k = 0;
whlie(i < an || j < bn) {
a[i] <= b[j] && i < na ? c[k++] = a[i++];
a[i] <= b[j] && i >= na? c[k++] = b[j++]; => a배열이 텅빔
a[i] > b[j] && j < nb ? c[k++] = b[j++];
a[i] > b[j] && j >= nb ? c[k++] = a[i++]; => b배열이 텅빔
}병합정렬의 전략
병합정렬은 병합을 수행하는 단위를 가장 작은 1에서부터 2배씩 늘려가면서 병합을 반복함으로 배열을 정렬하게된다.
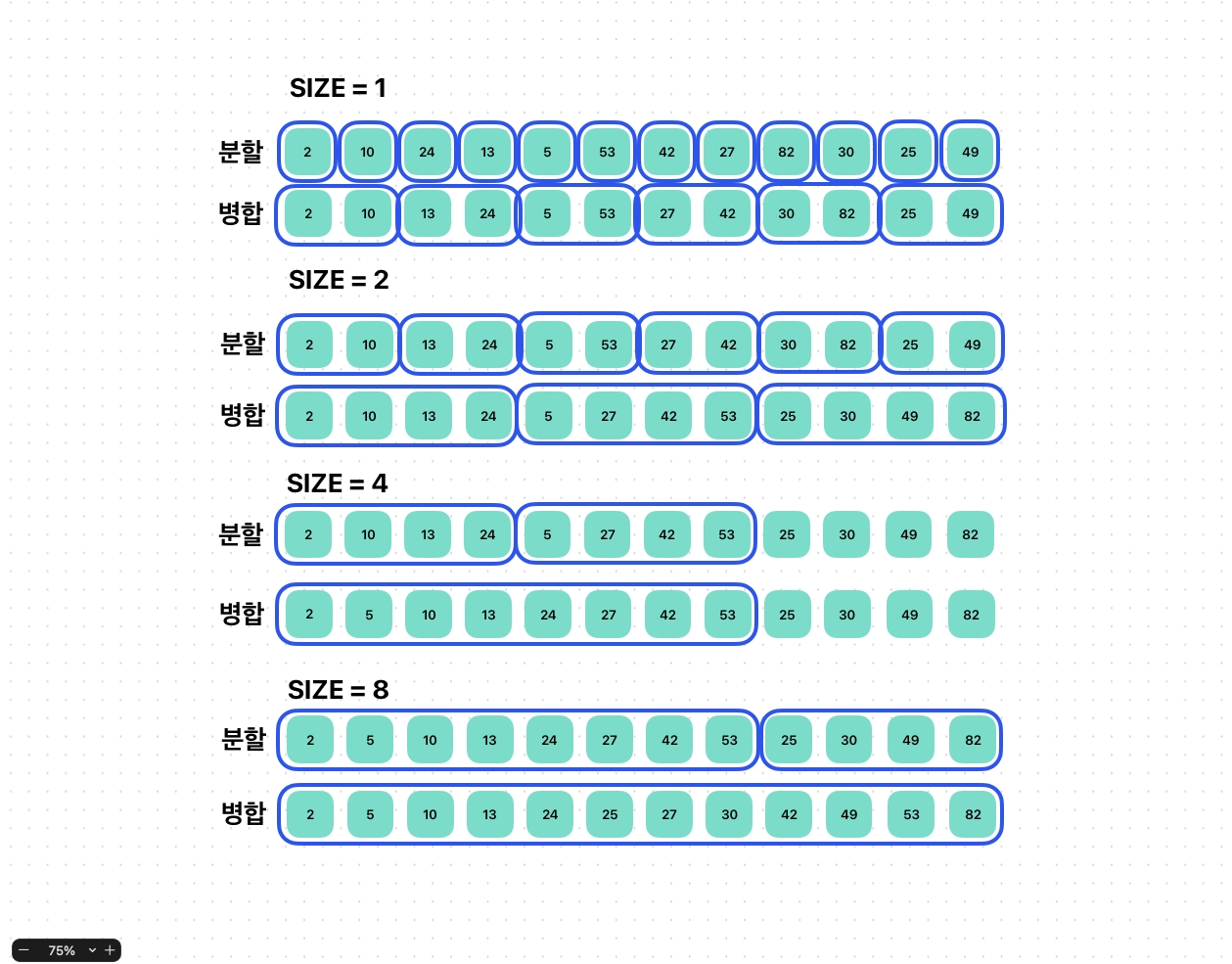
처음에는 1의 크기를 갖는 두 배열의 병합을 배열 전체에 대해서 실행하고, 다음에는 2의 크기를 갖는 두 배열의 병합을 배열 전체에 대해 실행한다.
그 다음으로는 크기가 4, 크키가 8 순으로 반복하다 크기가 N을 넘어가면 중단하면 된다.
- size = 1
- size가 N보다 작을동안
2.1 size의 크기로 배열을 분할해 두 분할씩 차례로 병합
2.2 size = size * 2
C로 구현
병합 정렬은 원리는 간단하지만 C로 구현하는거는 은근 빡쌘거같다.
서두에 말한거처럼 Python이나 Javascript같이 List를 slice할 수 있다면, 그냥 재귀함수로 List를 계속 반씩 쪼개가면서 더 이상 쪼갤 수 없을때 리스트를 머지하면 되는데, C로 구현 하려고 생각하니 memcpy까지 하면서 그렇게 해야하나? 라는 생각이 들었다.
일단 size가 4일때를 가정하고 그림을 먼저 그려보자.
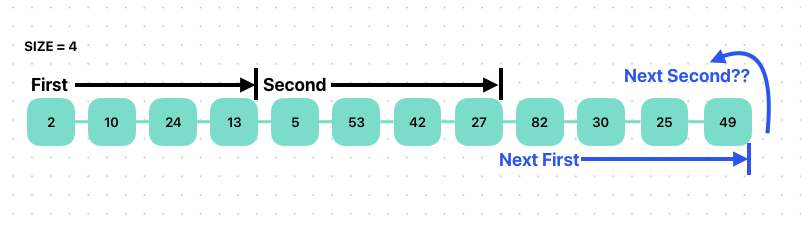
이렇게 병합을 위해서는 "2개의 병합할 배열이 필요하다"
근데 위에서 말한것처럼 list를 slice해서 잘라진 배열의 조각을 함수의 인자로 넘겨받아 merget sort하는게 아니기 때문에 조작이 까다롭다.
그래서 병합에 필요한 크기에 맞는 2개의 서로다른 배열을 구분하기 위해서 first, second라는 변수를 통해 위치를 가리키도록 한다.
first는 병합에 필요한 첫번째 배열을 가리키고, second는 병합에 필요한 두번째 배열을 가리킨다.
이렇게 병합을 완료하면 first 그리고 second는 size의 2배만큼 이동해 다음으로 위치한 병합해야할 첫번째 배열과 두번째 배열을 가리킨다.
다음으로 second가 배열의 범위를 벗어나 병합할것이 없게되면 병합을 마무리하게 된다.
이렇게 함수의 인자로 size별로 조각난 배열을 인자로 받아서 머지하는것이 아닌, 전체의 큰 배열을 조각내면서 병합을 하기때문에 병합에 필요한 서로다른 두개의 배열을 first와 second로 나타내게된다.
즉, 서로 다른 두 배열에 대해서 병합을 실시하지 않고, 한 배열 내에서 분할하면서 병합을 하기 위해 first, second라는 변수를 사용한다.
void merge_sort(int array[], int length) {
int i, j, k;
int first, second;
int *merged_array;
merged_array = (int *)malloc(sizeof(int) * length);
for(int size = 1; size < length; size *= 2) {
first = -2 * size; // 여기서 first가 0이 아닌 이유는, 아래 while문에서 size * 2 만큼 더하면서 0이 되기때문임
second = first + size;
// next second가 배열을 넘어가지 않는다면
while((size * 2) + second < length) {
first += size * 2;
second += size * 2;
i = first;
j = second;
k = first;
// 병합해야할 배열 [A] 와 [B]가 있을때, A와 B 배열에 합칠 배열에 저장해야할 요소가 남아있는 경우
// 즉 배열 [A], [B]의 병합이 완료되지 않았을 경우
// 여기서 배열 [A]는 First 구간을 의미하고, 배열 [B]는 Second 구간을 의미
while((i < first + size) || (j < second + size && j < length)) {
// [A] 배열의 요소가 B배열의 요소보다 작을경우
if(array[i] <= array[j]) {
// A배열에 있는 작은 요소를 머지 배열에 추가
if(i < first + size) {
merged_array[k++] = array[i++];
}
// A배열에 요소가 없기는경우, 즉 A배열은 정렬이 완료 되었으니 B배열 요소를 추가
else {
merged_array[k++] = array[j++];
}
}
// 반대로 B배열에 있는 요소가 A배열의 요소보다 작을경우
else {
// B배열의 요소가 남아있고, 인덱스가 배열을 초과하지 않았다면
if(j < second + size && j < length) {
merged_array[k++] = array[j++];
}
// B배열에 요소가 없는경우, 즉 B는 정렬이 완료되었으니 A배열 요소를 추가
else {
merged_array[k++] = array[i++];
}
}
}
}
for(i = 0; i < length; i++) {
array[i] = merged_array[i];
}
}
free(merged_array);
}전체 코드
//
// main.c
// MergeSort
//
// Created by 박재현 on 2024/07/04.
//
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void print_array(int array[], int length) {
for(int i = 0; i < length; i++) {
printf("%c ", array[i]);
}
printf("\n\n");
}
void merge_sort(int array[], int length) {
int i, j, k;
int first, second;
int *merged_array;
merged_array = (int *)malloc(sizeof(int) * length);
for(int size = 1; size < length; size *= 2) {
first = -2 * size; // 여기서 first가 0이 아닌 이유는, 아래 while문에서 size * 2 만큼 더하면서 0이 되기때문임
second = first + size;
// next second가 배열을 넘어가지 않는다면
while((size * 2) + second < length) {
first += size * 2;
second += size * 2;
i = first;
j = second;
k = first;
// 병합해야할 배열 [A] 와 [B]가 있을때, A와 B 배열에 합칠 배열에 저장해야할 요소가 남아있는 경우
// 즉 배열 [A], [B]의 병합이 완료되지 않았을 경우
// 여기서 배열 [A]는 First 구간을 의미하고, 배열 [B]는 Second 구간을 의미
while((i < first + size) || (j < second + size && j < length)) {
// [A] 배열의 요소가 B배열의 요소보다 작을경우
if(array[i] <= array[j]) {
// A배열에 있는 작은 요소를 머지 배열에 추가
if(i < first + size) {
merged_array[k++] = array[i++];
}
// A배열에 요소가 없기는경우, 즉 A배열은 정렬이 완료 되었으니 B배열 요소를 추가
else {
merged_array[k++] = array[j++];
}
}
// 반대로 B배열에 있는 요소가 A배열의 요소보다 작을경우
else {
// B배열의 요소가 남아있고, 인덱스가 배열을 초과하지 않았다면
if(j < second + size && j < length) {
merged_array[k++] = array[j++];
}
// B배열에 요소가 없는경우, 즉 B는 정렬이 완료되었으니 A배열 요소를 추가
else {
merged_array[k++] = array[i++];
}
}
}
}
for(i = 0; i < length; i++) {
array[i] = merged_array[i];
}
}
free(merged_array);
}
int main(int argc, const char * argv[]) {
int length;
int *array;
char *str = "TOLEARNSORTALGORITHM";
length = (int)strlen(str);
array = (int *)malloc(sizeof(int) * length);
for(int i = 0; i < length; i++) {
array[i] = str[i];
}
printf("Before MergeSorting.\n");
print_array(array, length);
merge_sort(array, length);
printf("After MergeSorting.\n");
print_array(array, length);
return 0;
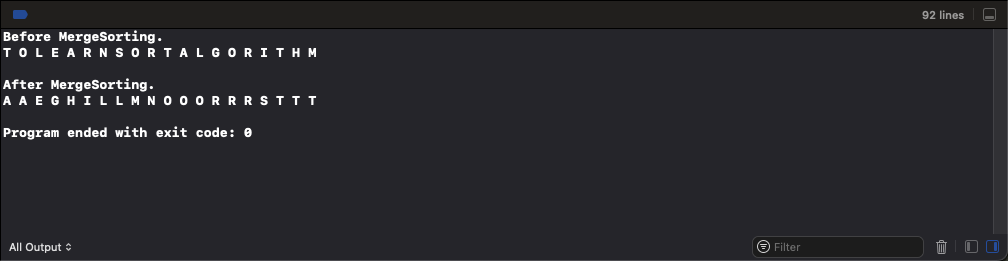
}실행결과

세상에 재현 님 벨로그가 7월 5일로 끝이라니 말도 안돼