Quick Sort

박재현·2024년 6월 27일
Cdata structure
1

Algorithm

목록 보기
21/22
post-thumbnail

아마 퀵 정렬이 정렬 알고리즘 중에서 가장 유명한(?) 정렬이지 않을까라는 생각이다.

라딕스 소트, 머지 소트는 못들어봐도 퀵 소트는 다들 한번씩 들어보는거 같은 기분이랄까?

일단 퀵 소트는 아주 빠른 속도를 보여주면서 동시에 원리도 간단한 아주 착한 알고리즘이다.

퀵 정렬은 간단히 말하면 연속적인 분할에 의해서 정렬된다. 분할의 의미는 단순히 정령를 위해 입력값으로 받은 배열을 쪼개는것이 아니라, 어떠한 축(Pivot)값을 중심으로 왼쪽은 이 축값보다 작은 값으로, 오른쪽은 모두 이 축값보다 큰 값으로 배열시키는 작업을 말한다.

이렇게한 다음 축값의 왼쪽과 오른쪽 부분을 각각 또 다시 분할하는 과정을 분할해야할 크기가 1이 될때까지 반복한다.

예를 들어보자!

먼저 편의를 위해서 분할의 축(Pivot)값은 가장 우측에 위치한 M이라고 하자.

그 다음으로 먼저 왼쪽부터 축값인 M보다 큰 값이 있는지 i를 1씩 증가시키면서 검사한다, 그 다음으로 오른쪽 부터는 M보다 작은 값이 있는지를 j를 1씩 감소 시키면서 검사한다.

// 왼쪽부터 기준값인 M보다 큰 값, 작은 값을 찾는다.

T O L E A R N S O R T A L G O R I T H M
i                                   j =

그러면 처음으로 걸린값은 T와 H이고, 이 두개의 값을 서로 바꾼다음 계속 i, j를 움직이면서 찾아나선다.

// i, j에 위치한 값을 서로 바꾼다.

H O L E A R N S O R T A L G O R I T T M
i                                   j =

다음으로 걸린 값은 O와 I인데, 이 두개의 위치도 서로 교환한다.

// i는 O를 찾고, j는 I를 찾는다.

H O L E A R N S O R T A L G O R I T T M
  i                             j     =
  
// i와 j의 위치를 서로 교환한다.

H I L E A R N S O R T A L G O R O T T M
  i                             j     =

그 다음으로 걸린 값은 R과 G인데, 이 또한 서로 위치를 교환한다.

// i는 R을 찾고, j는 G를 찾는다.

H O L E A R N S O R T A L G O R I T T M
          i               j           =
          
// 서로 교환한다.

H O L E A G N S O R T A L R O R I T T M
          i               j           =

그 다음으로 걸린 값은 N과 L인데, 이 또한 서로 위치를 교환한다.

// i는 N을 찾고, j는 L을 찾는다.

H O L E A G N S O R T A L R O R I T T M
            i           j             =
          
// 서로 교환한다.

H O L E A G L S O R T A N R O R I T T M
            i           j             =

그 다음으로 걸린 값은 S와 A인데, 이 또한 서로 위치를 교환한다.

// i는 S를 찾고, j는 A을 찾는다.

H O L E A G N S O R T A L R O R I T T M
              i       j               =
          
// 서로 교환한다.

H O L E A G N A O R T S L R O R I T T M
              i       j               =

그 다음으로 i는 오른쪽으로 한칸씩 이동하면서 M보다 큰 값인 O를 발견한다.

그리고 j는 왼쪽으로 한칸씩 이동하면서 A를 발견하게 된다.

이렇게 i와 j의 위차가 서로 같아지거나, i가 j보다 더 우측으로 가게 될 경우는 바로 분할이 완료가 된 경우를 말한다!!

따라서 이렇게 분할이 완료가 된 경우에는 i의 자리에 위치한 값 O와, Pivot값인 M을 서로 마지막으로 교환한다.

// i는 O를 가리키고 j는 A를 가리킨다. 
// i가 j보다 더 우측으로 가게 되었으니 분할은 완료가 된 상태다!

H O L E A G N A O R T S L R O R I T T M
              j i                     =
              
// 따라서 마지막으로 i자리에 위치한 O와, Pivot값은 M을 서로 교환한다.

H O L E A G N A M R T S L R O R I T T O
              j i                     =

그럼 i위치로 온 M을 기준으로 좌측은 모두 M보다 작은 값이고, 우측은 모두 M보다 큰 값이 위치한다.

이러한 분할 과정은 축값인 M을 중심으로 나누어지는 두 구간에 대해서 똑같이 적용한다.

즉 좌측 H부터 A까지의 구간을 가장 오른쪽값인 A를 축값으로 해서 위와 같은 분할 과정을 거친다.

그리고 우측의 R부터 O까지의 구간은 가장 오른쪽값인 O를 축값으로 해서 분할한다.

이러한 과정을 구간의 크기가 1이 될때까지 반복하면 정렬은 완료되게 된다.

그리고 구간의 구간을 나누는 과정은 재귀함수로 충분히 구현할 수 있다.

퀵 정렬 알고리즘 (array, length)
1. 만약 length > 1 이라면
- 1.1 length 크기의 배열 array를 분할해 축값의 위치를 mid로 넘긴다.
- 1.2 재귀 호출하여 (array, mid)
- 1.3 재귀 호출하여 (array+mid+1, length-mid-1)

여기서 mid값이 의미하는 부분은, 가장 마지막에 i와 j가 서로 엇갈리면서 분할이 완료되어서 i자리에 축값이었던 M이 오게되는데, 이때의 M이 위치한 값을 mid라고 한다.

따라서 (array, mid)가 말하는 바는 H~A까지, 즉 M의 좌측 구간을 말하고 (array+mid+1, length-mid-1)은 R~O까지, 즉 M의 우측 구간을 말한다.

C로 구현한 퀵 정렬

void quick_sort(int array[], int length) {
    int i,j;
    int temp;
    int pivot;
    
    if(length > 1) {
        pivot = array[length-1]; // 기준 값
        i = -1;         // i는 왼쪽부터 검색할 위치
        j = length-1;   // j는 오른쪽부터 검색할 위치
        
        // 분할
        while(1) {
            while(array[++i] < pivot);
            while(array[--j] > pivot);
            
            if(i >= j)  break;  // i와 j의 위치가 겹치거나 뒤바뀌면 분할 종료
            
            temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
        
        // 배열의 가장 끝에 위치한 기준 값과, i위치의 값을 서로 교환함
        temp = array[i];
        array[i] = array[length-1];
        array[length-1] = temp;
        
        quick_sort(array, i);
        quick_sort(array+i+1, length-i-1);
    }
}

코드를 보면 약간 Tree를 순회하는 방법 중 하나인 전위순회가 생각나기도 한다.

위 알고리즘대로 실행하면

  1. 처음으로 i와 j가 서로 교차될때 까지 분할을 한다.
  2. 처음 분할이 완료되면 가장 우측의 축값이 i의 위치로 온다.
  3. 그 이후로 i의 위치로온 첫번째 축값을 기준으로 좌측 구간을 분할을 시작한다.
  4. 좌측 구간 분할이 끝나면, 이동했던 첫번째 축값을 기준으로 우측 구간을 분할을 시작한다.

추가적으로 퀵소트는 안정성은 없다.

퀵정렬은 랜덤하게 섞여있는 난수 배열이나 아니면 절반정도 정렬된 배열에 대해서는 아주 좋은 속도를 보여준다.

하지면 이미 정렬된 배열이나 역순으로 정렬된 배열에 대해서는 너무너무 성능이 떨어진다.

정렬된 배열로 예를 들어보자.

위에 작성한 퀵쏘트 함수는 축값으로 먼저 배열의 가장 오른쪽 값을 선택했다.

그렇다면 이미 정렬된 배열의 경우 가장 큰 값을 축값으로 가지게 된다.

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 즉, 이 상태로 시작한다면 축값은 가장 우측인 10이되고, i를 먼저 1씩 증가시켜서 축값인 10보다 작지 않을때까지 증가시키게 된다.

그러면 i는 결국 가장 우측인 축값 혹은 축값과 같은 값에 위치하게 된다.

j는 당연히 1감소하고 보기때문에, i는 이미 j의 우측에 위치해있기에 분할은 종료되었다고 보고 i자리의 값과 축값을 서로 교환한다.

따라서 10이 위치한 자리에 10을 넣는다라는 소리고, 아무런 변화가 없다는 이야기가 된다.

즉 분할해야할 오른쪽 구간은 없고, 왼쪽 구간만 N-1의 크기로 된다.

이렇게 N-1크기의 왼쪽 구간은 또 왼쪽 구간내에서 가장 오른쪽에 위치한 값을 축으로 분할하므로, 또 다시 왼쪽 구간만 N-2의 크기로 된다.

이렇게 N번을 계속해서 재귀해 들어가야 정렬이 완료되고 분할도 제대로 이루어지지 않기 때문에 시간만 많이 걸리게 된다.

퀵 정렬의 이상적인 경우는 분할이 정확하게 구간을 양분하는 경우다. (그니까 배열 내에서의 중위값)

이 경우 재귀의 깊이는 log2N이고 가장 빠른 속도를 보여준다.

난수의 배열은 이렇게 이상적인 경우와 가까운데, 축값이 되는 가장 오른쪽 값이 그 구간에서 가장 작은 값 혹은 가장 큰 값이 될 확률이 정렬해야할 구간이 크면 매우 작아지기 때문이다.

이렇게 퀵 정렬은 분할할 축값이 어느 정도 그 구간의 중앙을 나누느냐에 성능이 좌우되지만, 일반적인 경우는 O(NlogN)의 평균 시간을 가지는 알고리즘이다.

퀵 정렬 개선

위의 퀵 정렬을 개선할 수 있는 몇가지 방법이 있다.

개념적으로 쉽게 이해할 수 있어서 구현에 큰 어려움은 없다고 생각해서 개선을 위한 코드를 별도로 작성하지는 않았지만 기록은 해두려고 한다.

1. 비재귀 함수로 수정

먼저 위에 작성한 퀵소트 함수는 재귀함수로 작성했다.

즉 재귀 호출로 인해서 Function Call Stack에 쌓인다는 소리다. 그래서 N이 늘어나면 스택의 크기도 같이 늘어나야 한다.

퀵소트의 가장 최악의 경우인 정렬된 배열 혹은 역으로 정렬된 배열의 경우 N번 재귀호출이 필요하기에 내부 메모리를 그만큼 사용하게 된다는 소리다.

이런 문제를 개선하기 위해서는 재귀함수를 사용하는 대신 직접 스택을 구현하면 된다.

(개인적으로 요즘 단말들 스펙들이 너무 좋아서 퀵쏘트 재귀함수 때문에 내부 메모리가 초과하는 일이 생길까? 싶기는 하다.)

스택으로 구현할때 유의해야할 부분이 있는데, 일단 FILO 구조라는 점을 유의해야 한다.

그리고 분할 해야할 구간을 재귀함수로 사용할땐 quick_sort(array+i+1, length-i-1); 이런식으로 int * 형과 int형 서로다른 2개의 데이터 타입을 사용했다.

그래서 스택을 사용할때는 시작하는 구간과 끝나는 구간, 즉 left, right의 index를 이용해서 구현해줘야 한다.

2. 난수 분할

퀵소트는 정렬된 배열 혹은 역으로 정렬된 배열에서 가장 안좋은 성능을 보인다는걸 우리는 알고있다.

그 이유가 축값을 배열의 가장 오른쪽 값을 선택하기 때문에, 결과적으로 가장 큰값 혹은 가장 작은 값이 축값이 되기 때문이고, 이럴 경우는 재귀가 깊어지고 메모리를 많이쓰고 재수없으면 OOM이 날지도 모른다.

이 문제를 해결하기 위해서는 축값을 잘 선택하면 된다.ㅋㅋ

하지만 입력되는 자료가 임의적인 것이기때문에 일관적인 방법으로 축값을 잘 선택하는 방법은없다.

그래서 축값은 랜덤하게 선택하는 것이 하나의 방법이다.

0부터 length-1 범위의 난수를 발생시키고, 이 발생시킨 난수의 값을 제일 오른쪽 요소와 서로 교환한 다음 퀵정렬을 수행하는 것이다.

left = 0;
right = length - 1;

rand = random(right-left+1) + 1;
temp = array[rand];
array[rand] = array[right];
array[right] = temp;

quick_sort();

3. 삽입 정렬 사용

삽입 정렬은 구현도 비교적 간단하고 작은 크기의 배열에서는 성능도 좋은 알고리즘이다.

퀵소트는 구간을 쪼개가면서 정렬을 하게되는데, 큰 구간은 퀵소트로 쪼개고, 작은 구간을 삽입 정렬을 사용하는건 어떨까?

추가로 삽입 정렬은 추가적인 메모리도 필요료 하지 않아서 이또한 장점이다.

그렇다면! 어느 정도 작아질때 삽입 정렬을 사용하는가가 남아있다.

정렬해야할 구간의 크기를 너무 크게 잡아버리면 삽입 정렬은 성능이 좋지 못하고, 또 정렬해야할 구간을 너무 작게 잡아버리면 삽입 정렬의 이점또한 많이 못가지고 가게된다.

동시에 삽입정렬은 교환을 자주하는 알고리즘이라서 교환해야할 레코드의 크기가 큰 경우는 불리하다.

여튼저튼 본론만 바로 말하면, 레코드가 작은 경우는 100~200개 정도가 효율이 좋다하고, 레코드가 크면 10~50개 사이가 효율이 좋다고 한다.

left = 0;
right = length-1;

if(right-left+1 > 200) {
// 정렬 해야할 구간의 크기가 200보다 크면
	quick_sort();
} else {
// 정렬 해야할 구간의 크기가 200보다 작으면
	insert_sort();
}

4. 세 값의 중위 값 사용

난수로 분할값을 정하는 방법 외에도 세 값의 중위(Three of Median)를 이용해서 퀵 정렬을 개선하는 방법도 있다.

세 값은 먼저 가장 왼쪽값 array[left], 그리고 가장 오른쪽 값 array[right], 그리고 중간의 값 array[(left+right)/2]을 의미한다.

이 세 값을 정렬해서 가장 작은 값을 왼쪽으로, 중간 값을 중간에, 가장 큰 값을 가장 오른쪽으로 옮긴다.

그 다음으로 중간값과 가장 오른쪽 바로 앞의 값(array[right-1])과 위치를 바꾼다.

그런 다음 array[right-1](원래는 중간값 이었음)로 분할을 시작하는데, 가장 왼쪽값인 array[left]는 array[right-1] 보다 작은 값인게 확실하다.
(왜냐하면 처음에 3개를 뽑아서 정렬해서 가장 작은 값이 array[left]이고, 중간값이 array[right-1]이고, 가장 큰 값이 array[right] 이니까)

따라서 분할해야할 구간을 left+1 ~ right-2로 줄일 수 있다.

이렇게 정렬해야할 구간에서 2개만 줄여도 재귀의 깊이도 줄어들 뿐 아니라, 정렬이된 배열이나 역순으로 정렬된 배열에서는 분할을 정확히 중앙에서 부터 할 수 있기에 이 방법을 사용하면 가장 속도가 빨라진다.

초기 배열: [3, 5, 1, 2, 9, 8, 7, 4, 10, 6]

세 값: 3, 8, 6
세 값을 정렬: 3, 6, 8

가장 작은 3을 array[0]에, 중간인 6을 array[5]에, 가장 큰 8을 array[9]로 이동

세 값 이동 배열: [3, 5, 1, 2, 9, 6, 7, 4, 10, 8]

중간값인 6을 오른쪽에서 2번째로 이동

세 값 이동 배열: [3, 5, 1, 2, 9, 10, 7, 4, 6, 8]

3과 6과 8은 정렬이 완료되기 때문에 분할해야할 범위를 5부터 6으로 줄일 수 있고, 축값은 6이된다.

전체 코드

//
//  main.c
//  QuickSort
//
//  Created by 박재현 on 2024/06/27.
//

#include <stdio.h>
#include <stdlib.h>
#include <string.h>


void print_array(int array[], int length) {
    for(int i = 0; i < length; i++) {
        printf("%c ", array[i]);
    }
    printf("\n\n");
}


void quick_sort(int array[], int length) {
    int i,j;
    int temp;
    int pivot;
    
    if(length > 1) {
        pivot = array[length-1]; // 기준 값
        i = -1;         // i는 왼쪽부터 검색할 위치
        j = length-1;   // j는 오른쪽부터 검색할 위치
        
        // 분할
        while(1) {
            while(array[++i] < pivot);
            while(array[--j] > pivot);
            
            
            if(i >= j)  break;  // i와 j의 위치가 겹치거나 뒤바뀌면 분할 종료
            
            temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
        
        // 배열의 가장 끝에 위치한 기준 값과, i위치의 값을 서로 교환함
        temp = array[i];
        array[i] = array[length-1];
        array[length-1] = temp;
        
        quick_sort(array, i);
        quick_sort(array+i+1, length-i-1);
    }
}

int main(int argc, const char * argv[]) {
    int length;
    int *array;
    char *str = "TOLEARNSORTALGORITHM";
    
    length = (int)strlen(str);
    array = (int *)malloc(sizeof(int) * length);
    
    for(int i = 0; i < length; i++) {
        array[i] = str[i];
    }
    
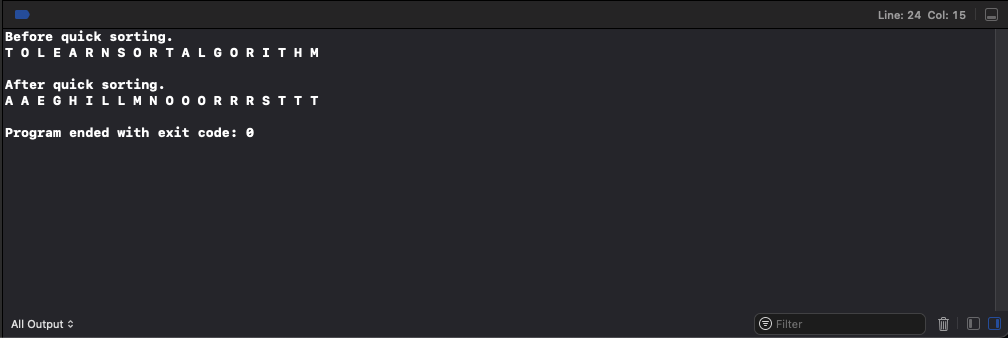
    printf("Before quick sorting.\n");
    print_array(array, length);
    
    quick_sort(array, length);
    printf("After quick sorting.\n");
    print_array(array, length);
    
    return 0;
}

실행 결과

profile
박재현
기술만 좋은 S급이 아니라, 태도가 좋은 A급이 되자
이전 포스트

분포수 세기 Distribution Count(Counting Sort)

다음 포스트

Merge Sort

0개의 댓글

관련 채용 정보