정렬
정렬(Sort)이란 임의의 순서대로 배열되어 있는 자료의 집합을 일정한 순서대로 재배열하는걸 의미한다. (모르는 사람은 없겠지?)
예를 들어서 1부터 10까지의 번호가 적힌 카드가 순서없이 배열되어 있다고 하면, 이때 오름차순(ascending order)으로 정렬한다고 하면 1,2,3,4 순서로 10까지 카드를 배열하는걸 말한다! (내림차순이면 당연히 반대겠지?)
정렬은 컴퓨터로 문제 해결을 하는데 있어서 검색과 함께 가장 많이 접하는 문제다.
그래서 알고리즘들 중에서는 가장 역사가 깊고, 연구가 많이 되어 왔고 가장 다양한 알고리즘들이 선택을 기다리고 있다.
일반적으로 가장 빠른 정렬 알고리즘은 퀵 정렬(Quick Sort)이라고 알려져 있고, 실제로도 빠른 속도를 나타낸다. 하지만 퀵 정렬은 거의 정렬이 되어 있는 자료에 대해서는 다른 기본적인 정렬 알고리즘(예를 들어서 삽입정렬)보다는 성능이 떨어진다.
이렇게 어떤 알고리즘이 가장 좋은 알고리즘이라는 일반해는 없고, 단지 주어진 상황과 여건에 가장 적합한 알고리즘이 있을뿐이다.
정렬 알고리즘의 다양성
정렬 알고리즘은 참으로 다양하다.
우선 정렬 알고리즘은 간단한것이냐, 복잡한것이냐에 따라서 관습적으로 나눌 수 있다.
간단한 알고리즘에는 선택 정렬, 삽입 정렬, 거품 정렬, 셀 정렬 등이 있고, 복잡한 정렬 알고리즘에는 퀵 정렬, 기수 정렬, 힙 정렬, 병합 정렬 등이 있다.
간단한 알고리즘은 안정되어 있고 구현이 쉬운 장점이 있으나 복잡한 알고리즘에 비해서 정렬 속도가 느리다.
반면에 복잡한 알고리즘은 구현에 어려움이 있거나 부차적인 메모리가 필요하기도 하지만, 일반적으로 단순한 알고리즘에 비해서 정렬 속도가 빠르다.
안정성(Stability)
정렬 알고리즘의 주요한 특징으로 안정성(Stability)이 있다.
안정성이란 같은 내용을 가지는 키값의 배열이 정렬 후에도 상대적 순서가 그대로 유지되면 그 알고리즘이 안정성이 있다고 하고 유지되지 않는 경우는 안정성이 없다고 한다.
안정성은 여러개의 키를 우선순위를 정해서 정렬하는 경우 알고리즘의 선택에 중요한 관건이 된다.
예를들어서 인사정보를 정렬한다고 가정하자.
그리고 정렬해야할 인사정보에는 이름, 사번, 나이, 와 같은 정보들이 저장되어 있을것이다.
만일 안정성이 있는 정렬 방법이라면 나이가 같은 "홍길동"과 "이춘향"에 대해서는 사번순으로 홍길동이 먼저 나오고 이춘향이 뒤에 나오게 될거다.
그러나 안정성이 없는 정렬 방법은 어느것이 먼저 나올지 알수가 없다.
이렇게 정렬을 여러가지 키로 하는것을 다중키(Multi-key) 정렬 이라고 하고, 여기에는 각각 키의 우선순위가 존재한다.
가장 높은 우선순위를 가지는 키를 1차 키(Primary key)라고 하고 정렬은 이 1차키를 대상으로 실시한다.
하지만 1차키의 값이 같은 레코드에 대해서는 다음으로 우선순위가 높은 2차 키(Secondary key)에 의해 정렬을 하게 된다.
이와 같은 다중 키(Multi key) 정렬에서 안정성이 있는 정렬 알고리즘을 사용할 경우 우선순위가 낮은 키부터 높은 순서로 여러번 정렬하면 자동적으로 다중키 정렬이 구현된다.
만일 안정성이 없는 정렬 방법을 사용할 경우에는 키값의 비교에서 우선순위대로 대소를 판별하는 방법이 포함되어야 한다.
선택 정렬 (Selection Sort)
드디어! 이번 포스팅의 내용인 선택 정렬!
위의 전반적인 정렬 알고리즘은 이전 포스팅인 Heap Sort에서 다루지 못했기 때문에 추가적으로 다뤘다.
여튼!
선택 정렬은 가장 간단한 정렬 알고리즘이다. 선택 정렬은 우리가 실생활에서 가장 많이 사용하는 알고리즘이기도 하다.
만약 순서없이 뒤죽박죽 섞인 카드 뭉치를 순서대로 정렬해봐! 라고 한다면 아마도 이 카드뭉치에서 가장 작은 카들르 찾아서 가장 앞으 두고, 다음으로 작은 카드를 찾아서 그 다음에 두고.... 를 반복하면 카드 뭉치가 정렬이 될거다.
이런 정렬 방법을 바로 선택 정렬(Selection Sort)라고 한다.
선택 정렬 알고리즘
일단 이후에 나오는 알고리즘은 기본적으로 정수형태의 배열을 정렬하는걸 원칙으로 하겠다.
다음은 선택 정렬을 하는 알고리즘이다!
- i = 0
- i가 n-2가 되면 끝낸다.
- 배열의 i항 부터 n-1항 까지 중 최소값을 찾아서 그 항을 min에 저장한다.
- 배열의 i항과 min항을 교환한다.
- i를 1 증가 시키고 2번으로 돌아간다.
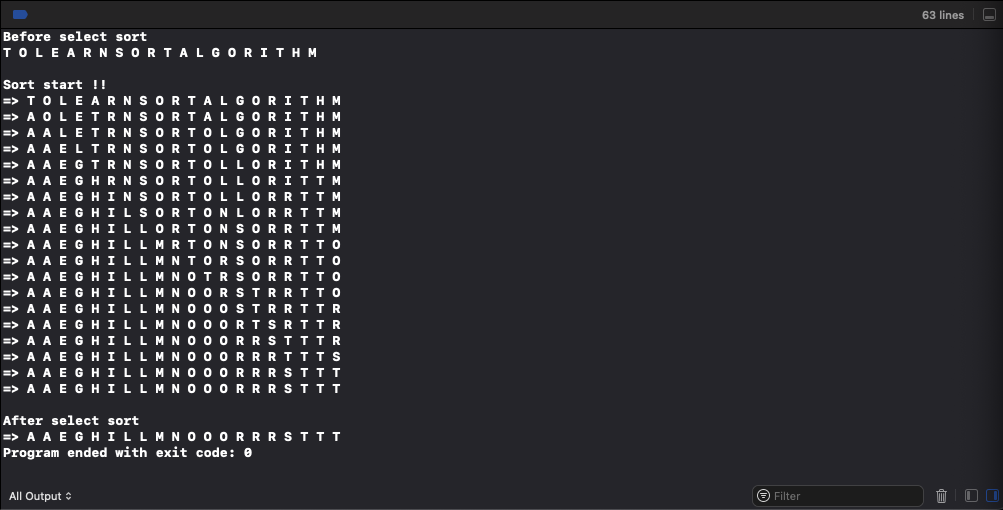
위 알고리즘 대로 "TOLEARNSORTALGORITHM" 이라는 문자열을 정렬하는 과정을 보자.
처음에는 최소값을 찾는 범위는 전체 범위가 되고, 최소값은 5번째 원소인 A가 된다. (같은 값이 여러개 나올때는 가장 앞에 위치한 값을 선택한다.)
이 A와 가장 앞의 T를 바꾸는것이 정렬의 첫단계다.
두번째 단계로 최소값을 찾는 범위를 O부터 끝까지가 되고, 최소값은 A가 되므로 역시 O와 A 두 값을 바꾼다.
세번째 단계의 범위는 L부터 끝까지가 되고, 최소값은 E가 되므로 L과 E 두개 값을 서로 바꾼다.
이 과정을 반복하는것이 바로 선택정렬 알고리즘이다!
한번 끝까지 추적해보자!
안정성 문제
안정성(Stability)이란 위에서 설명한것 처럼, 같은 키의 상대적 순서가 정렬 후에도 변함이 없을을 의미한다.
하지만 선택 정렬은 안정성이 없다.
위 문자열에서 T는 총 3개가 있는데 정렬이 완료되면 T의 순서는, 3번째가 1번째로, 1번째가 2번째로, 2번째가 3번째로 바뀌어 있다.
선택정렬과 같이 인접한 배열의 요소를 교환하지 않고, 뚝 떨어진 요소를 교환하는 경우에는 안정성이 없는 경우가 많다.
선택 정렬 알고리즘 실행 시간 분석

정렬을 해야할 N의 갯수가 1000개에서 2000개로 두배 늘어날때 실행 시간은 2의 제곱인 약 4배가 늘어나게 된다.
그래서 선택 정렬은 더 큰 N을 적용하는것은 무리가 있다.
하지만 N이 100 이하인 경우에는 만족할만한 속도를 보여준다.
선택정렬의 최악의 경우는 역순으로 저장된 배열인데, 이 경우 정확히 N번을 교환해야 하기 때문이다.
반면 최전의 경우는 이미 정렬된 배열이 되는데, 정렬이된 배열의 경우는 교환은 필요없고 대소 비교만 하면 되기 때문이다.
이렇게 선택 정렬은 Nx(N-1)/2번의 비교를 위해 시간을 다 잡아먹기 때문의 최악의 경우와 최선의 경우나 별 차이가 없고, 시간의 차이가 생기는 부분은 최소값을 교환하는 횟수일 뿐이다.
위 표를 보면 알겠지만 선택 정렬의 가장 좋은 경우와 최악의 경우 모두 O(N^2)의 시간보갑도를 보여주는데, 사실 2중 for문을 사용하기 때문에 O(N^2)의 시간복잡도가 나올거라는게 충분히 예상 가능하긴 하다.
전체 코드
//
// main.c
// Selection Sort
//
// Created by 박재현 on 2024/05/30.
//
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void print_array(int a[], int n) {
printf("=> ");
for(int i = 0; i < n; i++) {
printf("%c ", a[i]);
}
printf("\n");
}
void select_sort(int a[], int n) {
int min;
int min_index;
for(int i = 0; i < n - 1; i++) {
print_array(a, n);
min = a[i];
min_index = i;
for(int j = i + 1; j < n; j++) {
if(a[j] < min) {
min = a[j];
min_index = j;
}
}
a[min_index] = a[i];
a[i] = min;
}
}
int main(int argc, const char * argv[]) {
int length;
int *array;
char *str = "TOLEARNSORTALGORITHM";
length = (int)strlen(str);
array = (int *)malloc(sizeof(int) * length);
printf("Before select sort\n");
for(int i = 0; i < length; i++) {
array[i] = (int)str[i];
printf("%c ", array[i]);
}
printf("\n\nSort start !!\n");
select_sort(array, length);
printf("\nAfter select sort\n");
print_array(array, length);
return 0;
}실행 결과