재귀함수로 조합, 순열 구하다 갑자기 무슨 Heap Sort??
마음 같아서는 나도 Bubble Sort부터 Insert Sort 차례차례 하고싶지만, 인생은 내맘처럼 안되는법!ㅋㅋ
사정이 생겨서 먼서 빠르게 Heap에 대해서 정리를 하게 되었다.
여튼 그래서 Heap Sort에 대해서 정리해보고 알아보자.
Heap Sort
엉덩이할때 힙이 아니다!
Heap은 우선순위큐의 일종으로 우선순위가 높은 요소를 효율적으로 선택할 수 있는 자료구조를 의미한다.
???: 우선순위큐가 뭔데 씹덕아?

우선순위큐는 일단 조금 뒤에 다시 이야기해보자.
일단 본포스팅에서는 힙은 나무 구조로 구현하고, 이 나무구조는 linked list가 아닌 배열을 이용해서 구현할 예정이다.
힙정렬은 추가적인 메모리(Extra Memory)가 전혀 필요없으면서도 O(NlogN)의 성능을 보여주는 매우 빠른 정렬 방법이고, 입력되는 자료에도 거의 무관하게 고른 성능을 보여주는 뛰어난 알고리즘이다.
왜 Linked List가 아니라 배열을 이용해서 구현하나? 🧐
그 부분은 아래에서 설명해보겠다!
아! 그리고 센스있는 사람이라면, Heap Sort가 O(NlogN)이니까, Heap은 O(logN) 이겠네? 라는것도 유추할 수 있을듯하다.
우선순위 큐 (Priority Queue)
우선순위 큐는 어떤 특정한 자료 구조를 의미하는게 아니다. 허허허.
다만 자료의 집합이 있고, 이 자료는 각각의 우선순위(Priority)가 존재하는 형태를 의미한다.
그리고 우선순위큐는 다음과 같은 7개의 동작이 정의되는 경우가 많다.
- 생성(Construct): 주어진 N개의 자료로 우선순위 큐를 생성한다.
- 삽입(Insert): 우선순위 큐에 새로운 자료를 삽입한다.
- 제거(Remove): 순위가 가장 높은 자료를 제거한다.
- 대치(Replace): 순위가 가장 높은 자료와 새로운 자료를 대치한다.
- 변경(Change): 자료의 순위를 변경한다.
- 삭제(Delete): 임의의 자료를 삭제한다.
- 결합(Join): 두 우선순위 큐를 결합하여 큰 우선순위 큐를 만든다.
위 7개의 기본 동작 중에서는 다른 기본 동작에 의해서 정의된것들이 많다.
예를 들어서 대치(Replace) 동작은 삭제(Remove와) 삽입(Insert)을 이어서 하는것과 동일하다.
또 변경(Change)는 삭제(Delete)와 삽입(Insert)을 이어서 하는것과 같고, 생성(Construct)은 N번의 삽입(Insert)을 하는것과 동일하다.
스택과 큐는 넓은 의미에서 우선순위 큐의 예시가 될 수 있다.
스택은 여러개의 자료의 집합이며 가장 나중에 삽입(Insert)된 자료가 가장 우선순위(Priority)가 높다.
스택의 대표적인 동작인 팝(Pop) 동작은 바로 우선순위가 가장 높은(가장 나중에 들어온) 자료를 제거(Remove)하는 것과 같으며, 푸쉬(Push) 동작은 삽입(Insert) 동작과 같다.
큐도 동일하다.
흔히들 우선순위 큐에 대해서 오해하는 점은 우선순위 큐가 어떤 구체적인 자료 구조라고 생각하는 부분인데, 우선순위 큐는 말 그대로 우선순위에 의해서 순서가 유지되고 관리되는 자료 구조의 추상적인 개념이다.
아직도 이해가 잘 안되는 사람을 위해서 짧고 굵게 정리해보자면!
우선순위 큐는 우선순위가 높은것을 먼저 빼는것을 의미하고, Queue의 선입 선출 이런거 다 필요없고, 데이터가 언제 들어가던지간에 우선순위가 가장 높은것이 먼저나오는 자료구조를 의미한다.
단! 우선순위가 동일할 경우에는 선입선출이 보장되어야 한다!
이제는 이해가 되었을거라고 생각한다.
힙(Heap) 이란?
힙은 우선순위 큐의 1번부터 5번까지의 동작이 정의되어 있으며 우선순위는 키값의 크기에 의해 정해지는 자료구조다.
그리고 힙은 어떤 키가 다른 특정한 두 키보다 큰값을 가져야 한다는 조건이 만족해야 한다. (최대힙)
그래서 힙은 나무 구조와 자연스럽게 연결된다!
나무 구조에서 부모의 키는 두 자식의 키값보다 크게 만들어주면 자연스럽게 힙의 구조가 되는것이다~
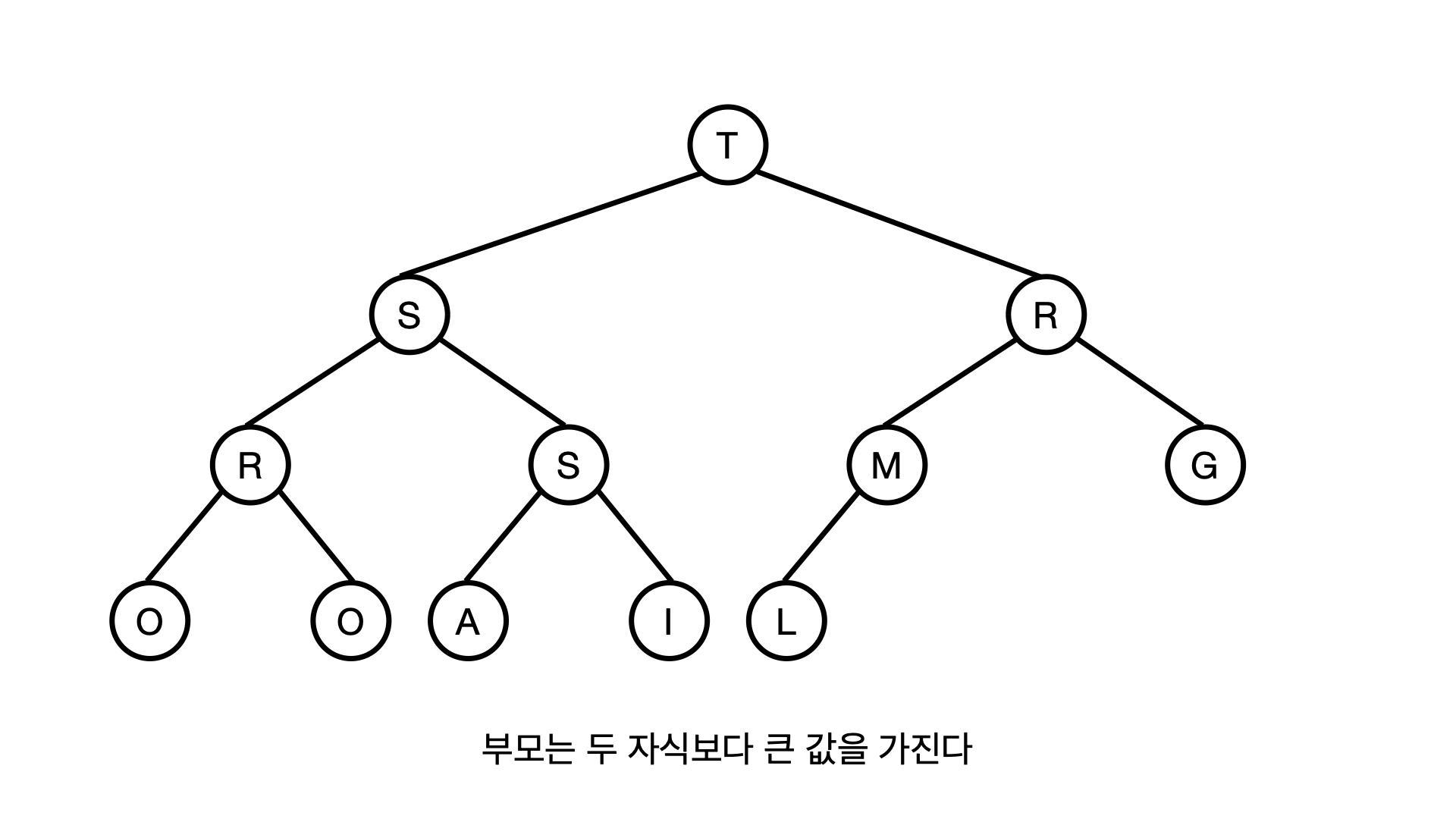
위 그림은 "SORTALGORITHM" 이라는 12개의 문자를 힙으로 구성한 예시이다.
힙의 뿌리는 전체 레코드(노드) 중에서 가장 큰 레코드(노드)가 된다.
그리고 뿌리의 자식은 뿌리 다음으로 큰 두개의 레코드가 되고, 이 규칙은 아래 노드에서도 동일하게 적용된다!
잘 보면, S가 가장 먼저 Insert가 되겠지만 T가 가장 높은 우선순위를 갖고 있다는걸 눈치채야 한다.
위 그럼처럼 완성된 힙에 Z라는 자료를 삽입(Insert) 해보자!
일단 Z는 힙의 가장 말단에 추가되어야 하는데, 좌측 노드에서부터 차례대로 추가가 되어야 한다.
여튼 Z를 힙의 가장 말단에 추가 하게되면 힙의 규칙에 위배된다.
왜냐하면 Z의 부모노드인 M은 Z보다 작은 값이기 때문에, Z와 M노드가 서로 자리를 바꿔야 한다.
이제는 R이 Z의 부모가 되었는데, R이 Z보다 값이 작기때문에 또 이 두 노드의 값을 서로 바꿔야 하고 Z는 한칸 위로 올라간다.
이제 Z의 부모는 T가되고, T역시 Z보다 작은 값이기 때문에 두개의 노드가 서로 자리가 바뀌게 된다.
결국 Z는 뿌리의 자리를 차지하게 되는데, Z가 힙의 값중에서 최대값이기 때문이다.
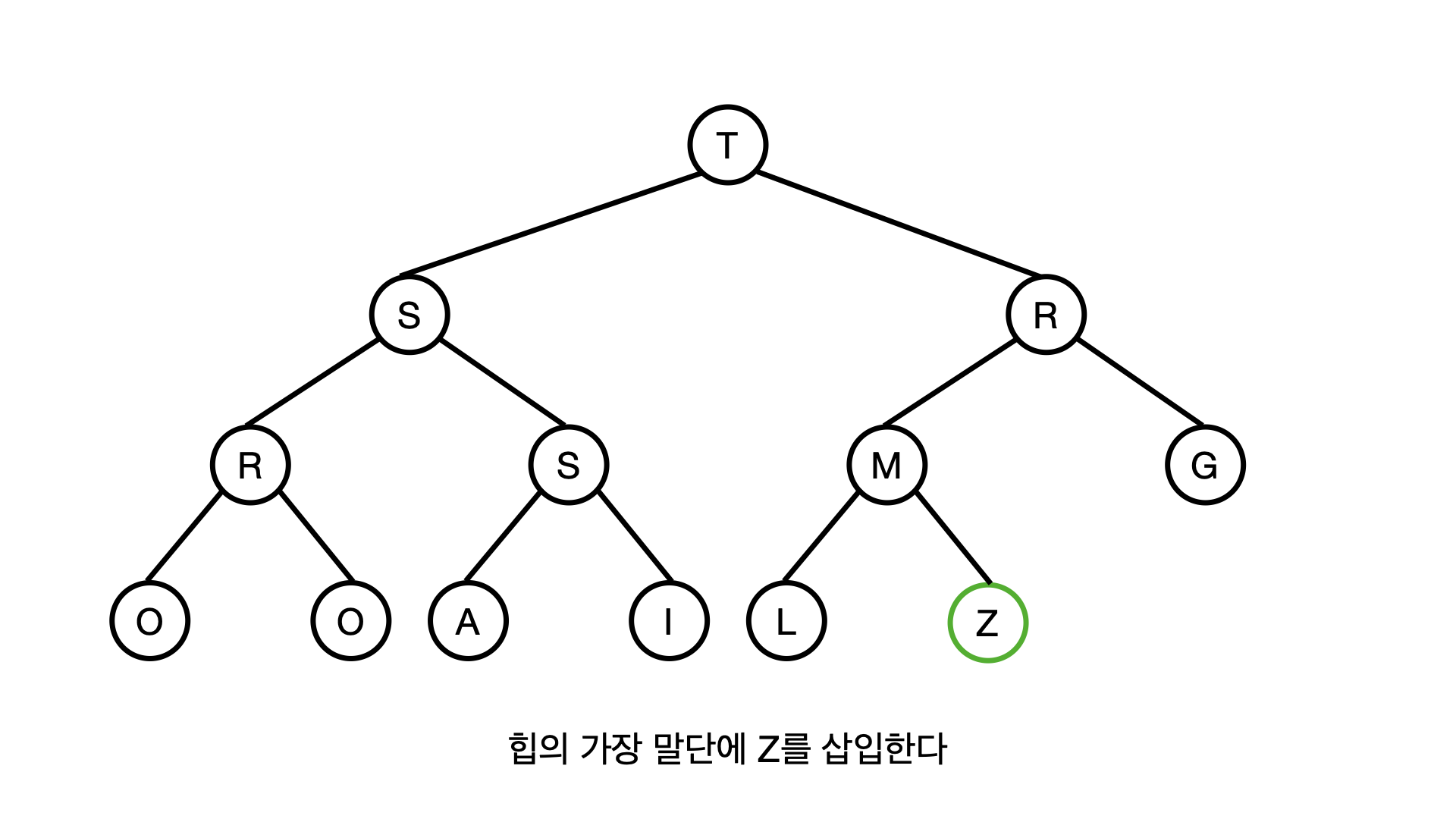
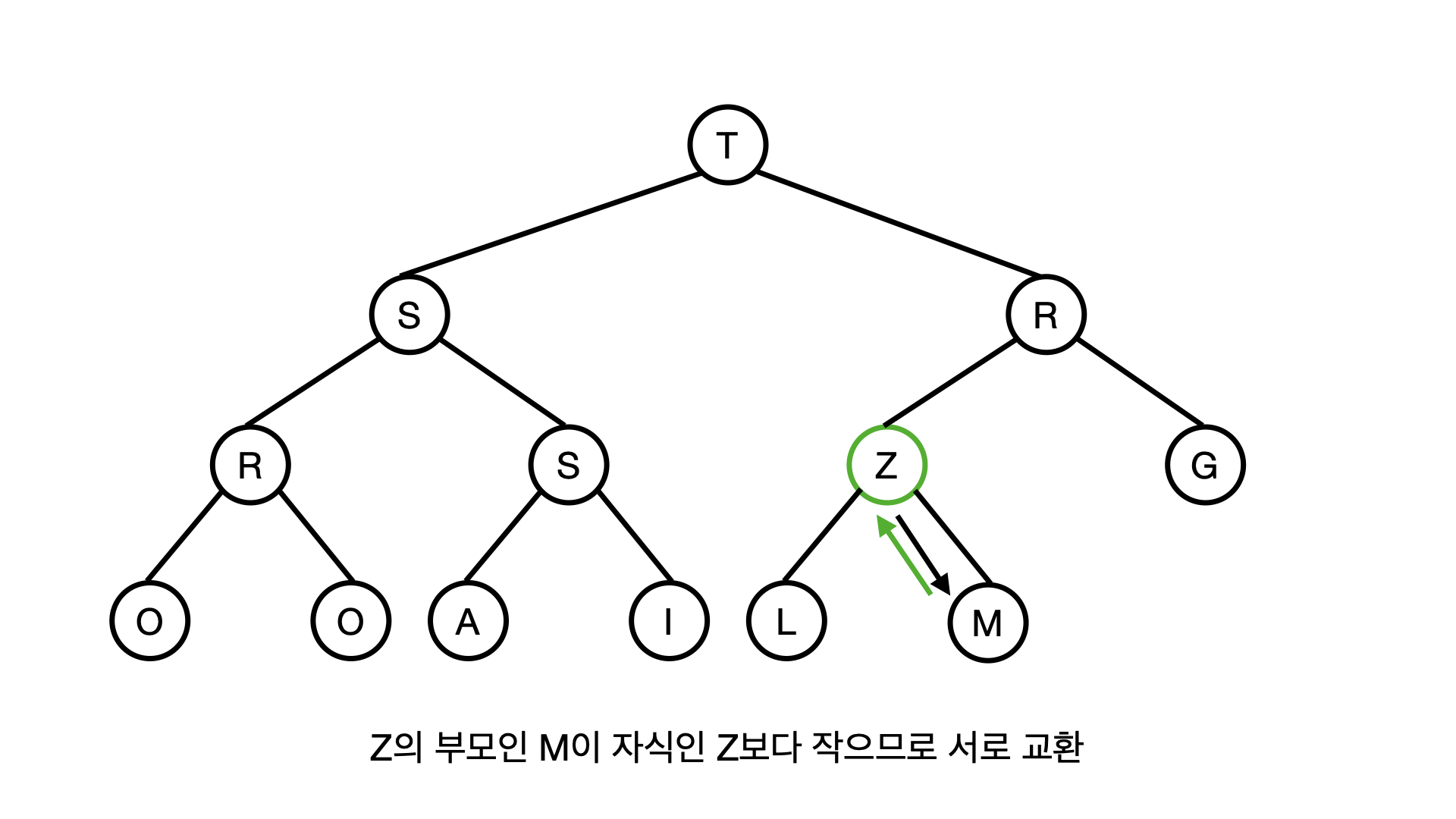
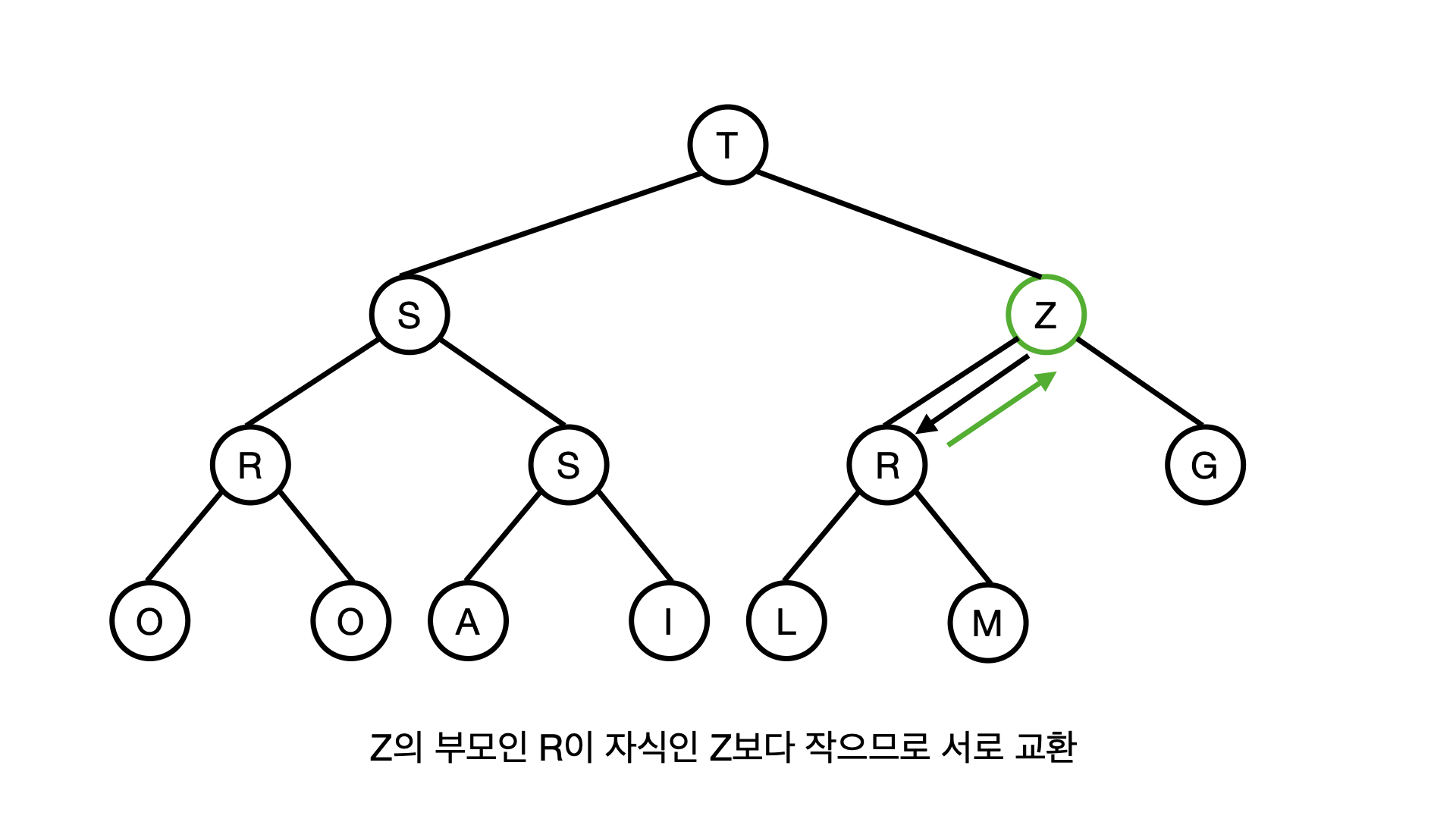
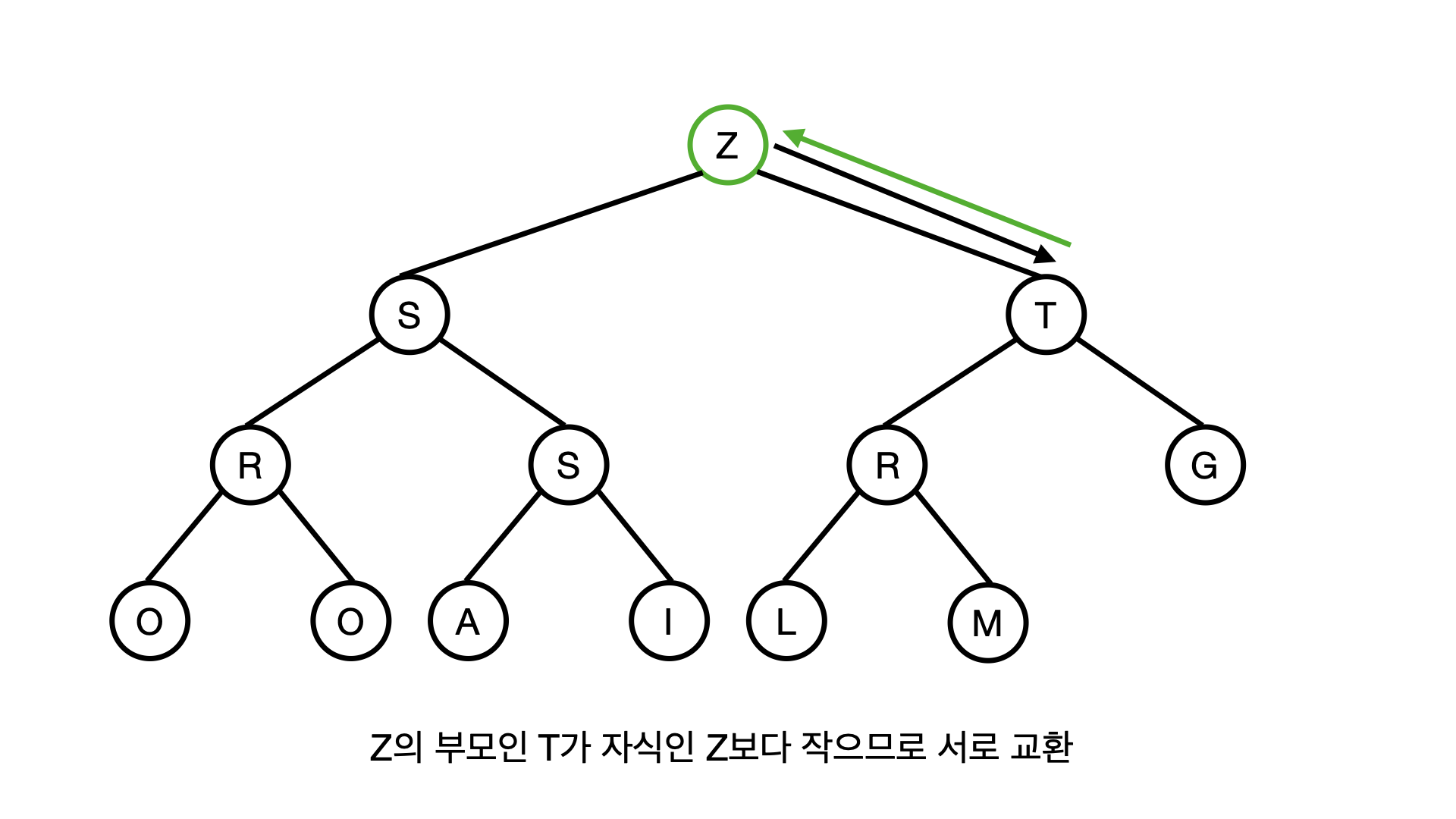
이렇게 새로 삽입된 Z가 힙의 규칙에 맞춰서 지위가 상승하는 작동을 Z를 UPHEAP 한다 라고 표현단다.
UPHEAP 동작을 잘 기억해두자!
다음으로 힙에서 가장 큰 자료를 제거(Remove)하는 동작을 정의해보자!
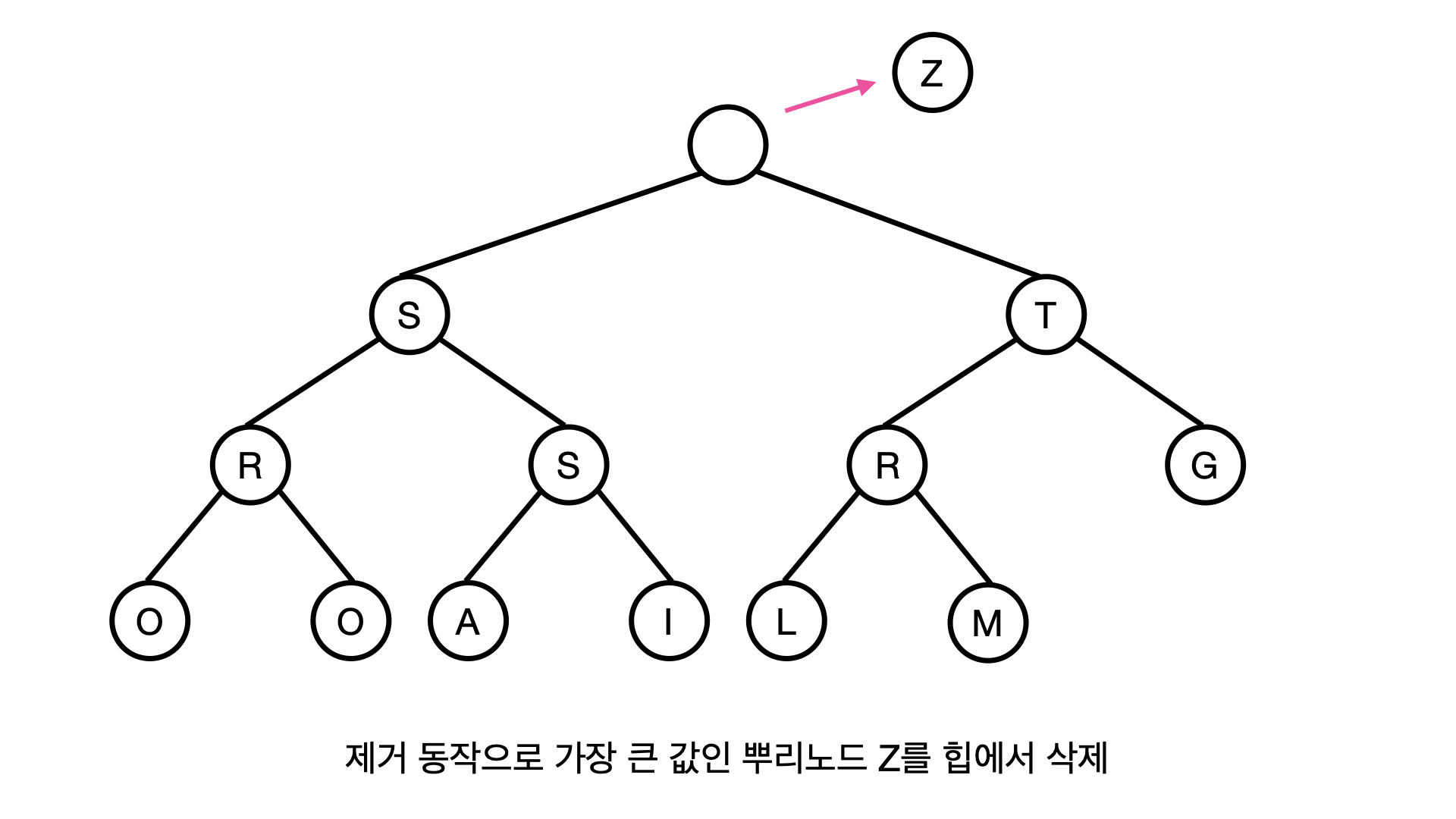
현재 힙에서 제일 큰 자료는 뿌리의 값이다. (왜냐면 최대힙이니까!)
따라서 현재 뿌리는 Z이므로 일단 힙에서 Z를 제거해보자, 그러면 뿌리가 없는 이상한 나무 구조가 되어버린다, 그래서 힙의 가장 말단 값인 M을 일단 뿌리에 둔다.
그러면 나무 구조의 모양은 유지가 되었지만 힙의 규칙에는 위배되는데, M의 자식인 S와 T는 모두 부모인 M보다 크기 때문이다.
이때 M을 대신할 뿌리를 찾아야 하는데, 이는 두개의 자손 중에서 제일 큰 T가 되어야 한다.
만약 S가 뿌리 노드로 온다면 S의 자손이 T가 되게되고, T는 S보다 크기때문에 힙의 규칙에 위배가 되기 때문이다.
이렇게해서 T와 M은 서로 교환해 위치가 변한다. 다음에 M의 자식은 R과 G인데, R은 M보다 크므로 힙의 규칙에 어긋난다.
그래서 R과 M을 서로 교환한다. 다음으로 M의 자손은 L인데, L은 M보다 작으므로 힙의 규칙을 만족하기 때문에 이제 M은 제자리를 찾게됐다.
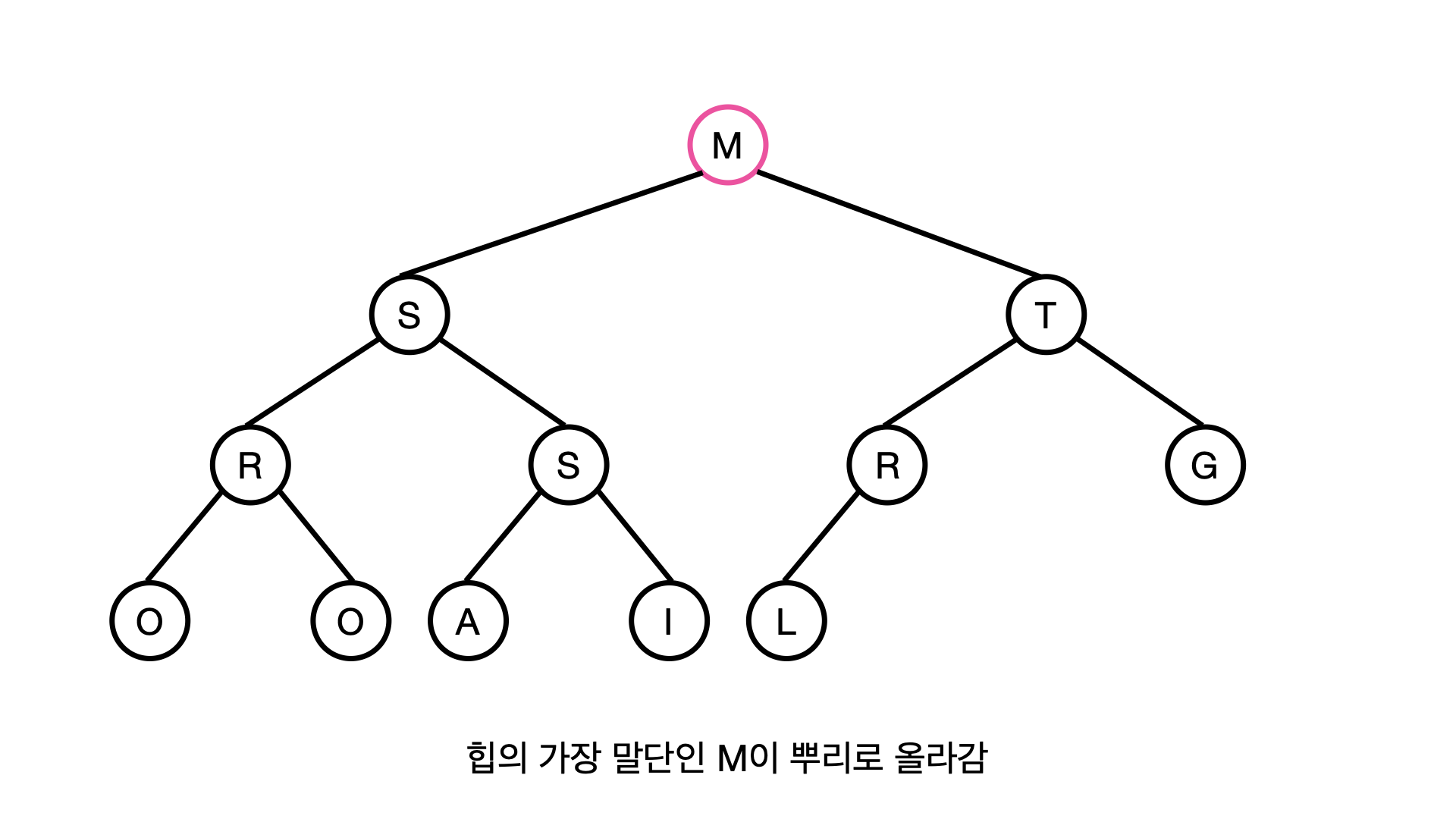
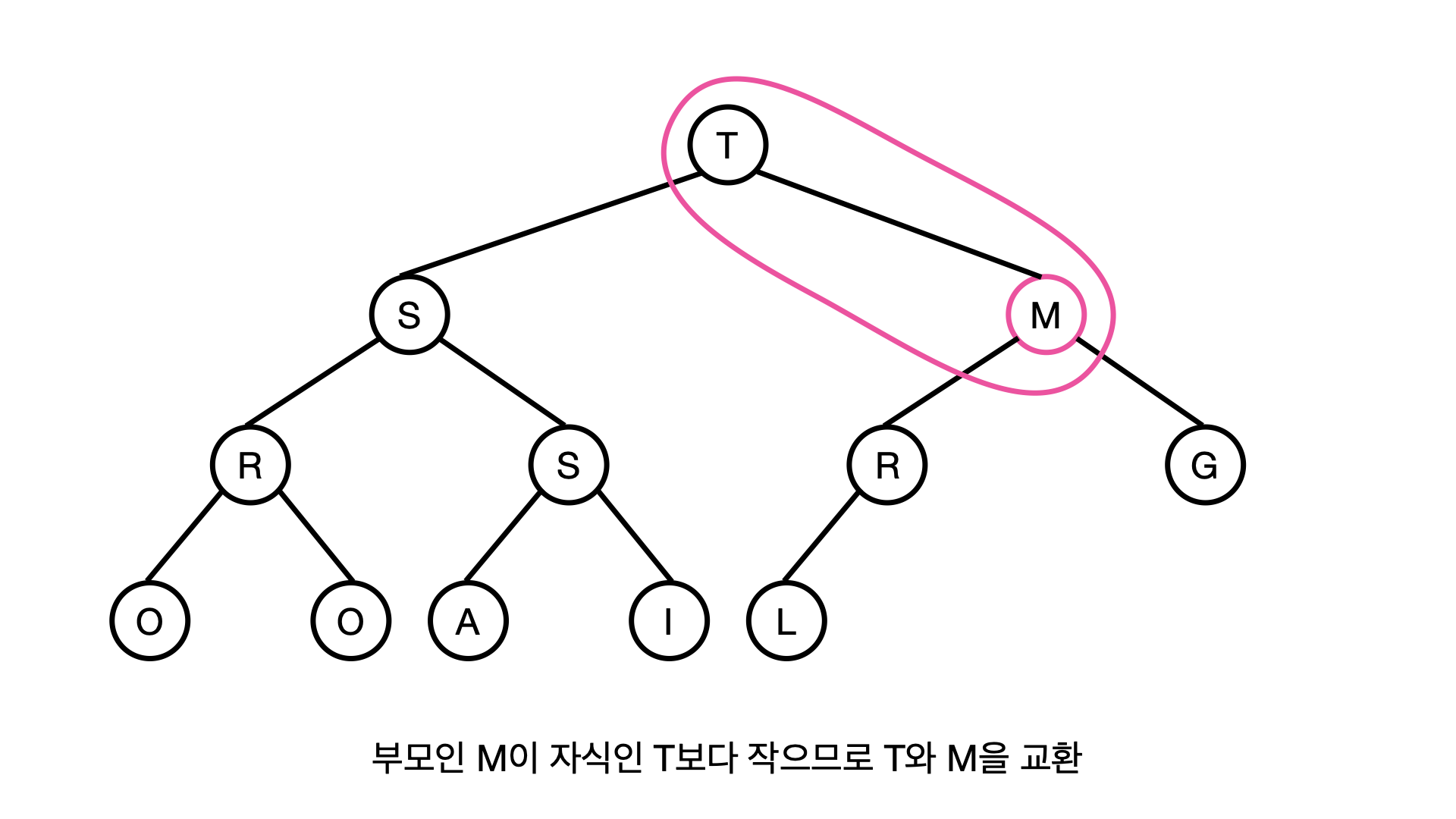
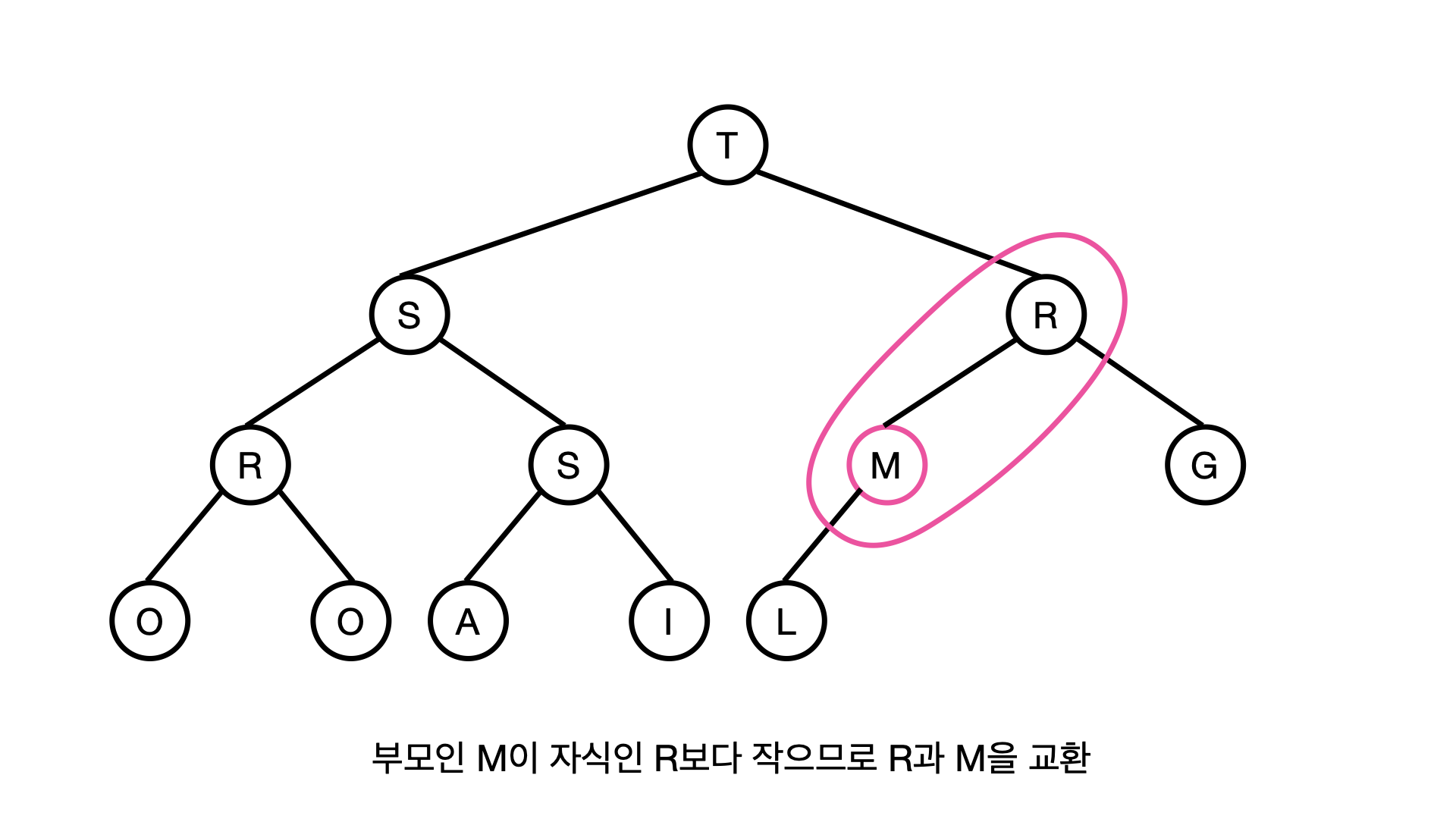
이렇게 힙의 상단을 차지하던 M을 힙의 규칙에 맞게 적절한 위치로 끌어 내리는 동작을 M을 DOWNHEAP 한다라고 표현한다.
DOWNHEAP동작도 잘 기억해두도록 하자!
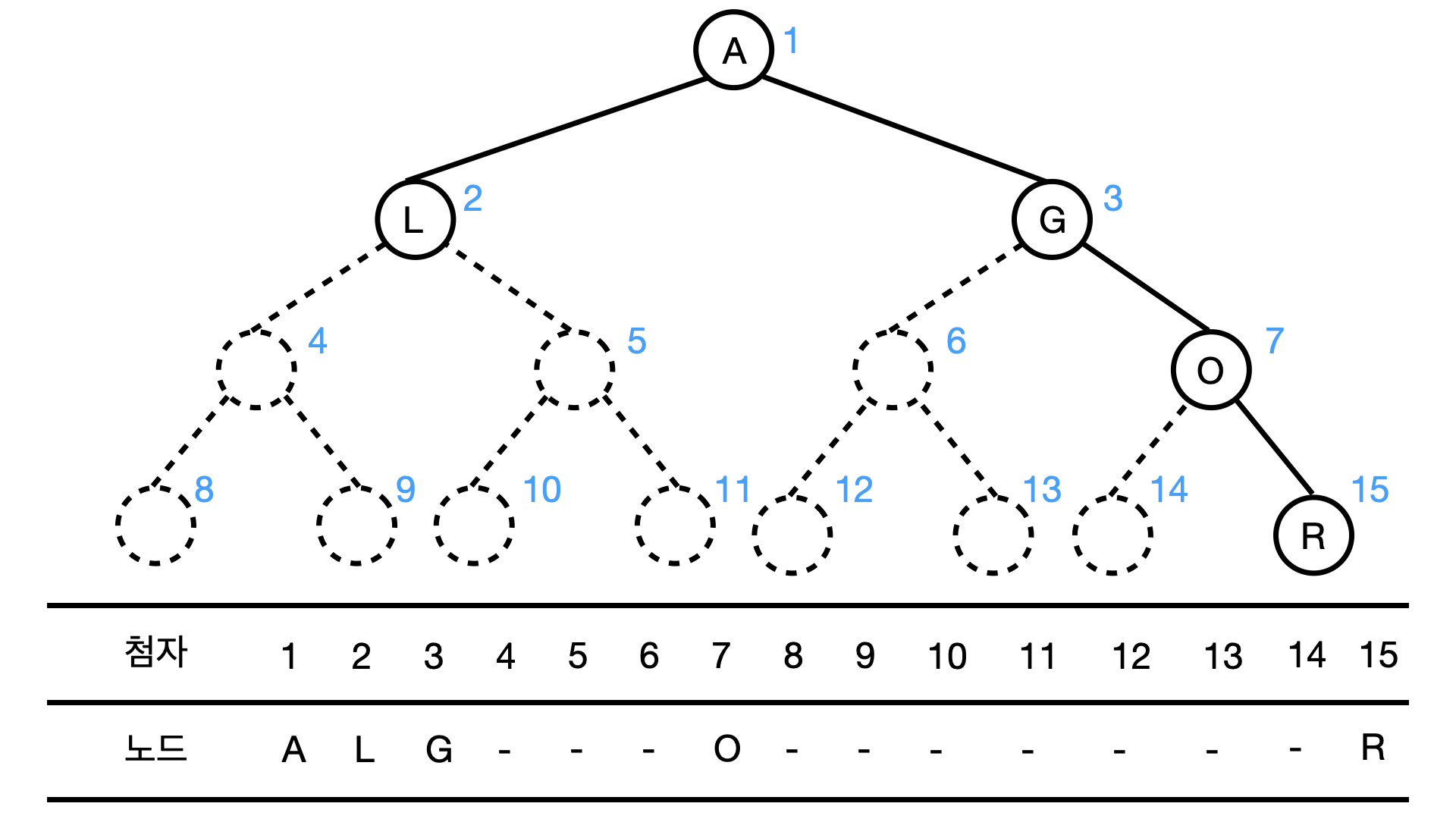
트리 구조를 배열로 구현하는 법
나무 구조를 구현하는 방법에는 연결 리스트를 이용하는 방법과 배열을 이용하는 방법이 있다.
연결 리스트는 부모와 자식관의 관계를 포인터를 이용해 직접적으로 결합시키지만, 배열을 이용하는 방법은 첨자(index)의 조작으로 간접적으로 부모 자식간을 연결시켜준다.
일단 아래 그림과 같이 힙 구조에 층별로 나무를 타는(Level-order Travlers 혹은 BFS) 방법으로 각 노드에 1번부터 번호를 부여해보자.
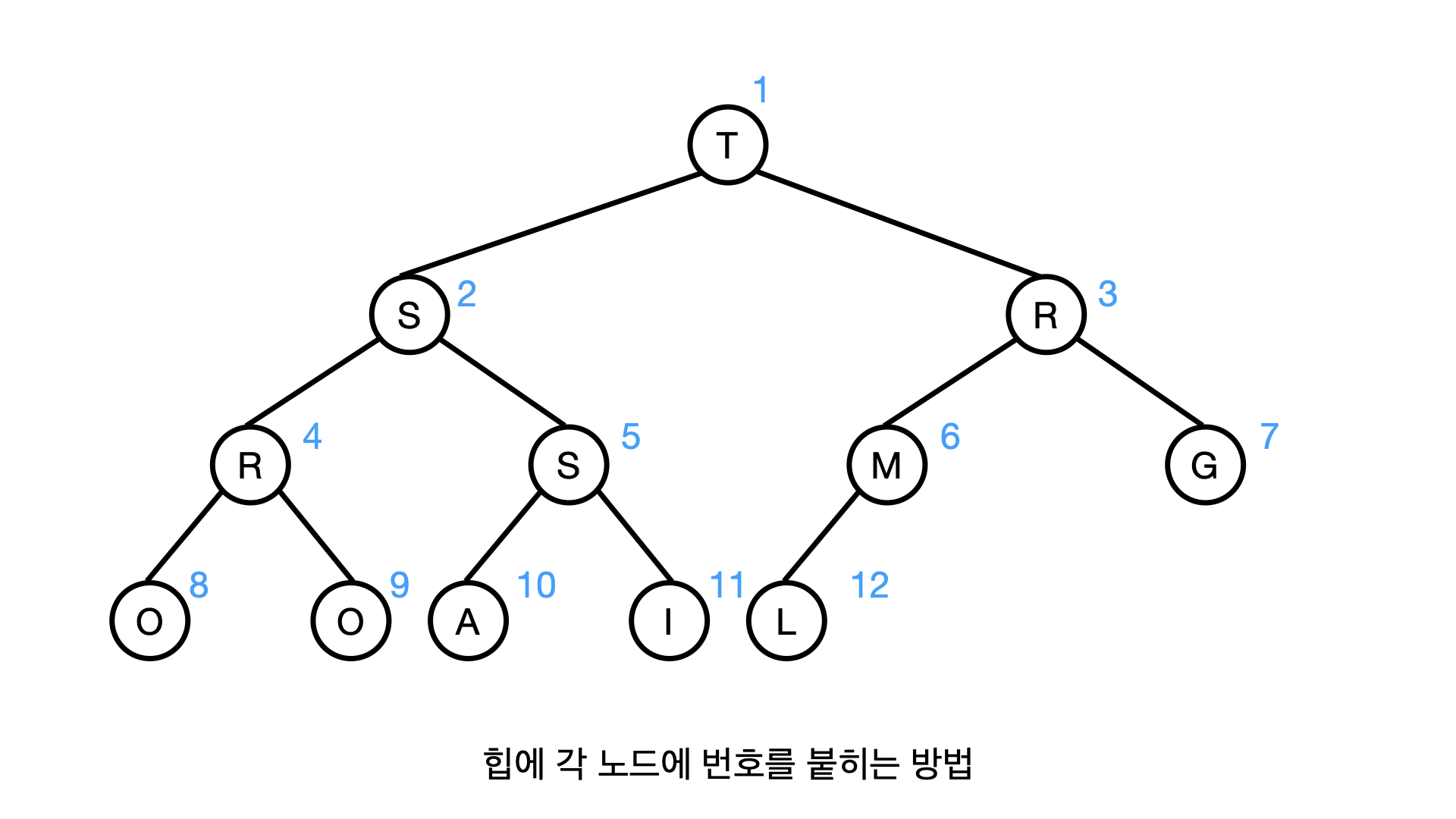
이렇게 번호를 붙혀두면, 이진 나무 구조(Binary Tree)의 경우 다음과 같이 부모와 자식간의 관계를 나타낼 수 있다.
- 번호 j를 갖는 노드의 부모의 번호는 j/2 이다.
- 번호 j를 갖는 노드의 왼쪽 자식의 번호는 jx2이고, 오른쪽 자식은 jx2+1 이다.
- 힙 자료의 갯수 n의 절반(n/2)까지가 내부 노드이다.
예를 들어서 번호 2번의 S노드의 왼쪽 자식은 2x2=4의 번호를 갖고있는 R이며, 오른쪽 자식은 2x2+1=5의 번호를 갖는 S가 된다.
반대로 4의 번호를 갖는 R의 부모는 4/2=2의 번호를 갖는 S가 되고, 번호 5를 갖는 S의 부모는 5/2=2의 번호를 갖는 S가 된다.
또한 위 3개 규칙중 3번 규칙은 DOWNHEAP의 구현에 필수적인데, 위 그림을 자세히보면 노드의 갯수가 12개이고, 12/2=6까지의 노드가 내부 노드(Internal Node)가 된다.
내부 노드란 자식을 가지고 있는 노드를 의미하고, 자식을 가지지 않는 말단의 노드를 외부노드(External Node 혹은 Leap)라고 한다.
이 번호를 배열의 첨자(index)라고 생각하면 다음과 같이 힙 구조는 배열로 선형적으로 저장할 수 있다!
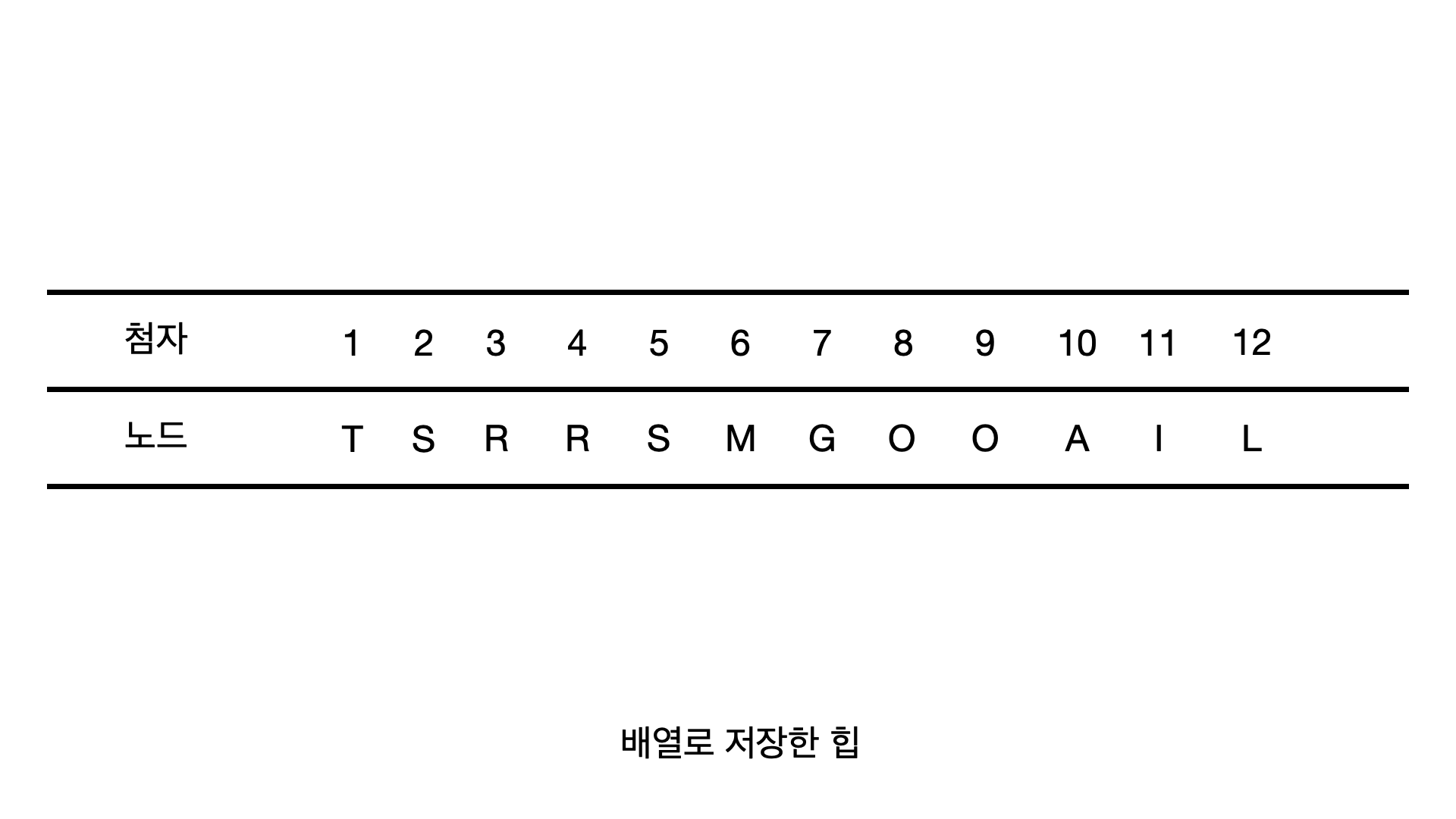
배열로 나무 구조를 저장하는 방법은 연결리스트를 이용하는 방법에 비해서 링크를 저장할 공간이 필요없고 구현이 간단하기 때문에 이점이 있다!
하지만 나무 구조가 균현이 잡혀있지 않은 경우(Unbalanced)에는 실제로 없는 노드를 위해서 배열 공간을 확보해야 하는 문제점이 생긴다.
그래서 배열을 이용하는 방법은 규현이 잡힌(Balanced) 나무 구조에 한해서 사용할 수 있다.
즉 Complete Binary Tree 구조에 한해서 사용할 수 있고, Heap은 Complete Binary Tree 구조로 만들어야 한다는 소리다.
아래 그림으로 극도로 균형이 잡히지 않은 나무 구조에 대해서 배열로 구현하면 얼마나 많은 메모리를 낭비하는지 확인해보자.
겨우 5개 노드를 저장하기 위해서 무려 15개의 배열 공간이 필요하게 되므로 10개의 공간을 낭비하게 된다. (심지어 뿌리 노드를 0번이 아닌 1번 인덱스부터 저장한다면 11개의 공간을 낭비하게 된다.)
하지만! 힙에 대해서는 이런 점을 우려하지 않아도 된다.
왜냐하면 힙은 위에서 정의한것 처럼 완전하게 균형이 잡힌 나무 구조를 나타낸다. 따라서 연결 리스트를 사용하지 않고 배열을 사용하면 링크의 공간이 절약될뿐 아니라 구현도 간단하고 속도도 향상될 수 있다.
힙 생성
이제 실제로 힙을 생성하는 과정을 따라가보자!
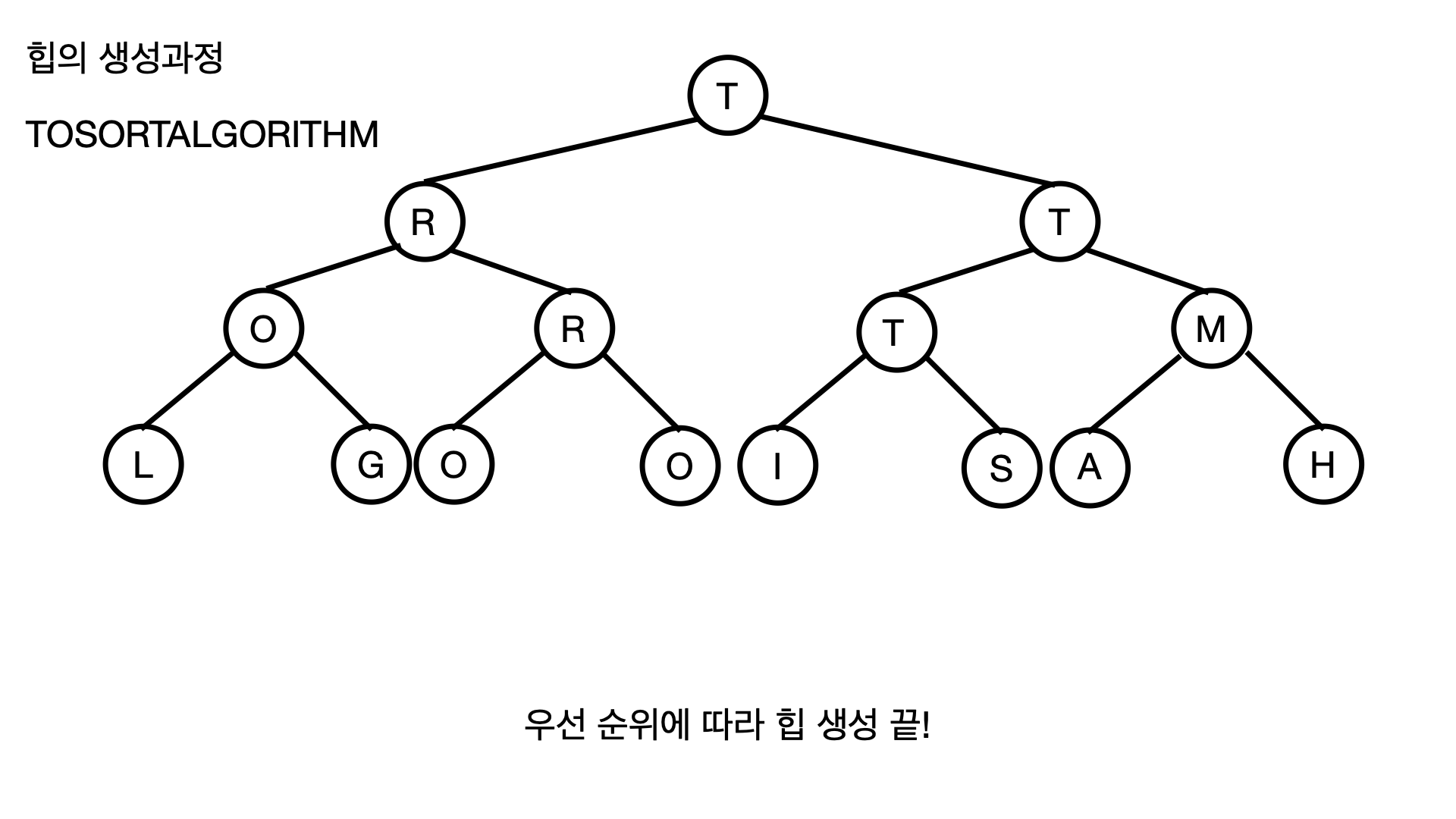
먼저 힙을 생성할때는 우선순위에 맞게 정렬하면서 힙을 생성하게 되는데, 하양식 힙 생성 방법으로 자료를 순서대로 읽어서 힙의 말단에 두고 그것을 계속 UPHEAP 하게 된다.
위에서 언급한 UPHEAP을 기억해내야 한다!
정렬할 데이터는 "TOSORTALGORITHM" 이라는 문자열이다!

결과적으로 아래 사진과 같이 힙이 정렬되면서 만들어진걸 확인할 수 있다.
힙 제거
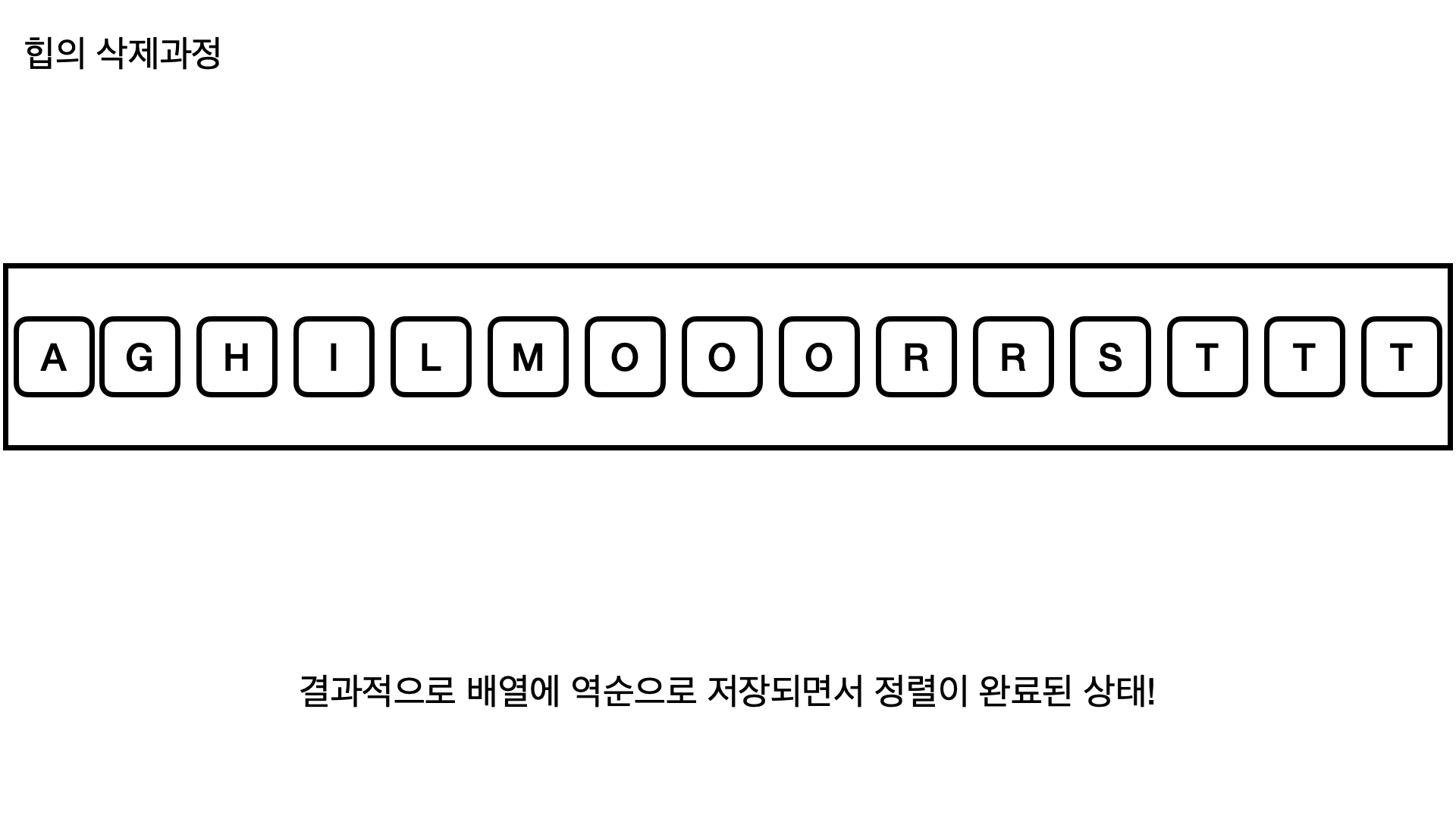
이렇게 힙을 우선순위에 따라 생성을 했다면, 정렬할 준비가 완료된 상태고 정렬을 하는 방법은 이미 힙이 우선순위에 따라서 생성했기 때문에 가장 큰 값을 차례대로 뽑아서 역순으로 저장하면 끝난다!
여기서 큰 값을 뽑는다는건 힙에서 원소 하나를 삭제한다는것을 의미하고, 뽑은값을 역순으로 저장하면 오름차순이 되고 그대로 저장하면 내림차순이 된다.
하지만 내림차순으로 하게 될 경우 추가적인 배열 공간이 필요하기때문에, 역순으로 저장하는것이고 자연스럽게 오름차순으로 정렬이 된다.
아마 아래 코드를 살펴보면 충분히 이해할수 있을거라고 생각한다.
여튼 아래 힙을 제거하는 과정은 DOWNHEAP이라는 과정의 반복인데, 위에서 설명한 DOWNHEAP을 상기시키면서 아래 영상을 확인해보자!
결과적으로 우선순위큐를 이용한 힙을 삭제하면 아래와 같이 힙에 있는 값들이 자연스럽게 정렬되는걸 확인할 수 있다!
C로 구현한 힙정렬
먼저 UPHEAP과 DOWNHEAP 동작들을 정의해야 나머지 동작들을 구현할 수 있다.
아래의 upheap 함수는 힙을 저장한 배열과 위치를 상승시킬 노드의 번호(첨자, index)를 인자로 받아 조건에 맞게 위치를 상승시키는 함수다.
void uphead(int a[], int k) {
int v = a[k];
a[0] = INT_MAX;
while(a[k/2] <= v) {
a[k] = a[k/2];
k /= 2;
}
a[k] = v;
}v라는 변수에 노드가 가지고 있는 값을 저장하는데, 이때 이 값이 우선순위 결정에 사용할 값이다.
힙을 배열에 저장할때는 그 번호가 1번에서부터 시작하기 때문에 자연스럽게 배열의 첨자(index)를 1부터 자료가 저장된다.
그래서 배열의 첫째 요소 a[0]은 비게 된다.
이 a[0]를 보초로 이용하면 더욱 효율적인데, a[0]에 아주 큰 값을 넣어두면 k의 값이 0으로 들어가는 경우가 사라지게 되어서 k > 0 이라는 조건을 제외할 수 있다.
결과적으로 uphead 함수는 부모 노드의 값이 현재 위치를 상승 시키고자 하는 노드의 값보다 작으면 계속해서 부모를 타고타고 올라가게 된다.
그래서 반복이 끝나게 되면 자연스럽게 부모보다 작은 값을 가지는 위치에 가게된다.
void downheap(int a[], int n, int k) {
int i;
int v = a[k];
while(k <= n/2) {
i = k * 2; // 왼쪽자식
if(a[i + 1] > a[i] && i < n) // 오른쪽 자식이 왼쪽 자식보다 크다면 오른쪽 자식을 선택!
i++;
if(v >= a[i]) // 현재 아래로 내리고 싶은 노드의 값이 자식보다 크거나 같으면 힙의 조건을 만족해서 중단
break;
a[k] = a[i];
k = i;
}
a[k] = v;
}다음으로 downheap 함수다.
힙을 저장한 배열과, 전체 노드의 수 n과, 아래로 내릴 노드의 번호 k를 인자로 받는다.
눈여겨 봐야하는 것은 "내부노드"만 확인하는 것인데, 이유는 내부노드들만 자식들을 가지고 있기 때문이다.
그리고 인자로 받는 n은 배열의 전체 크가기 아니라 힙에 저장된 노드의 갯수임을 잊으면 안된다.
void insert(int a[], int *n, int v) {
a[++(*n)] = v;
uphead(a, *n);
}삽입동작은 매우 간단한데, 힙의 가장 말단에 새로운 노드를 추가하고, 해당 노드를 upheap 시키면 된다~
여기서 인자로 들어오는 n은 힙의 노드의 갯수를 의미한다.
그래서 n을 1증가시키고 해당 위치에 새로운 값을 추가하면 된다.
int extract(int a[], int *n) {
int v = a[1];
a[1] = a[(*n)--];
downheap(a, *n, 1);
return v;
}삭제하는 함수다.
remove 라는 이름은 reserved name이라 사용할수 없어서 extract라는 이름으로 함수를 작성했다.
삭제하는 과정도 단순한데, 힙에서 가장 큰 값, 즉 뿌리 노드인 1번 노드를 삭제하고 뿌리에 가장 말단에 위치한 값을 위치시킨 다음 downheap 동작으로 옳바른 위치를 찾도록 하면 된다.
void heap_sort(int a[], int n) {
int i;
int hn = 0; // hn은 힙의 노드 수. n은 배열의 크기다
for(i = 1; i <= n; i++)
insert(a, &hn, a[i]);
for(i = hn; i >= 1; i--)
a[i] = extract(a, &hn);
}이제 힙을 정렬할 준비가 모두 끝났기 때문에, 실제로 정렬을 해보자!
먼저 함수를 자세히 보면 알 수 있듯이 힙의 저장을 위해서 별다른 공간을 사용하지 않고 인자로 들어오는 a배열을 그대로 이용하고 있다.
이런 이유로 힙 정렬은 추가적인 메모리가 전혀 필요하지 않는다.
여튼 위 정렬하는 함수의 동작을 보면 배열 a에 차례대로 우선순위를 확인하면서 값을 저장한 다음, 높은 우선순위에 맞춰서 값을 하나씩 빼와 배열에 역순으로 저장하는걸 확인할 수 있다.
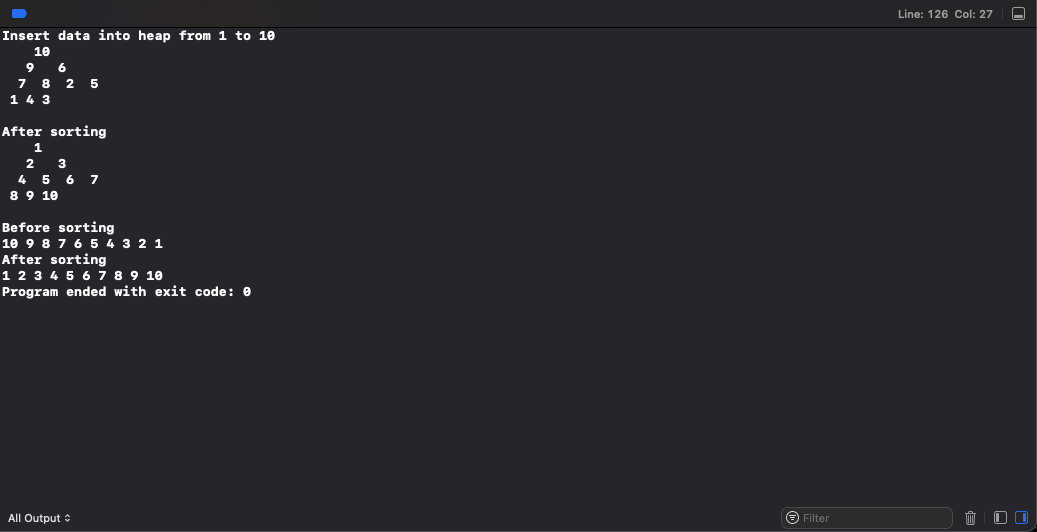
결과적으로 1부터 10까지 차례대로 힙에 저장하면 아래와 같은 모양으로 힙이 생성된다.
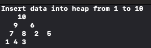
그리고 이렇게 만들어진 힙을 정렬하면 아래처럼 1부터 10까지 차례대로 정렬된다.
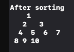
결과적으로 힙정렬은 O(NlogN)의 뛰어난 성능을 가지면서 다른 알고리즘과 다르게 추가적인 메모리가 전혀 필요하지 않다는 점에서 좋은 알고리즘이다.
개선을 할 수는 없을까? 🧐
위의 힙 정렬을 개선하는 방법으로 상향식 힙 생성(Buttom-up Heap Construction)이라는 것이 있다.
위에서 본 방법은 하향식 힙 생성이라는 방법인데, 이는 힙의 크기가 0이라고 가정하고 힙의 크기를 삽입을 통해 증가시켰다.
하지만 상향식 힙 생성은 "처음부터 힙의 크기를 배열의 크기와 같이 잡고 DOWNHEAP을 통해 힙을 힙 조건에 맞게 수정하는 방식으로 힙을 생성한다"
무슨말이냐??
배열은 a[1]부터 a[N]까지 이미 저장되어 있으므로 이것을 바로 힙이라고 가정하고, 각각의 노드에 대해 DOWNHEAP을 적용하면 힙 구조가 완성된다는 소리다.
사실 정렬을할때 빈 배열에 값을 추가하면서 정렬하는것 보다는, 이미 랜덤하게 배치된 배열을 정렬하는 경우가 더 빈번하지 않은가?
바로 이럴때 사용할 수 있는 방법이다.
그리고 DOWNHEAP은 내부노드에 한해서만 적용하면 되는데 왜냐하면 외부노드는 자식이 없기 때문에 자식과 부모를 비교할 필요가 없고, 지위가 하강할 여지가 없기 때문이다.
또 DOWNHEAP은 배열의 크기(= 힙의 크기)를 2로 나눈 번호의 노드, 즉 내부 노드의 가장 말단 부터 뿌리까지 순서대로 적용하면 된다.
이렇게 되면 빈 배열에 값을 하나하나 채워 넣으면서 힙을 생성하는 것보다 훨씬 간편하고, 힙을 생성할 필요가 없기 때문에 UPHEAP 동작을 생략할 수 있다!
믿기 힘들겠지?? 나도 그랬다ㅋㅋ 하지만 실제로 그려보자!
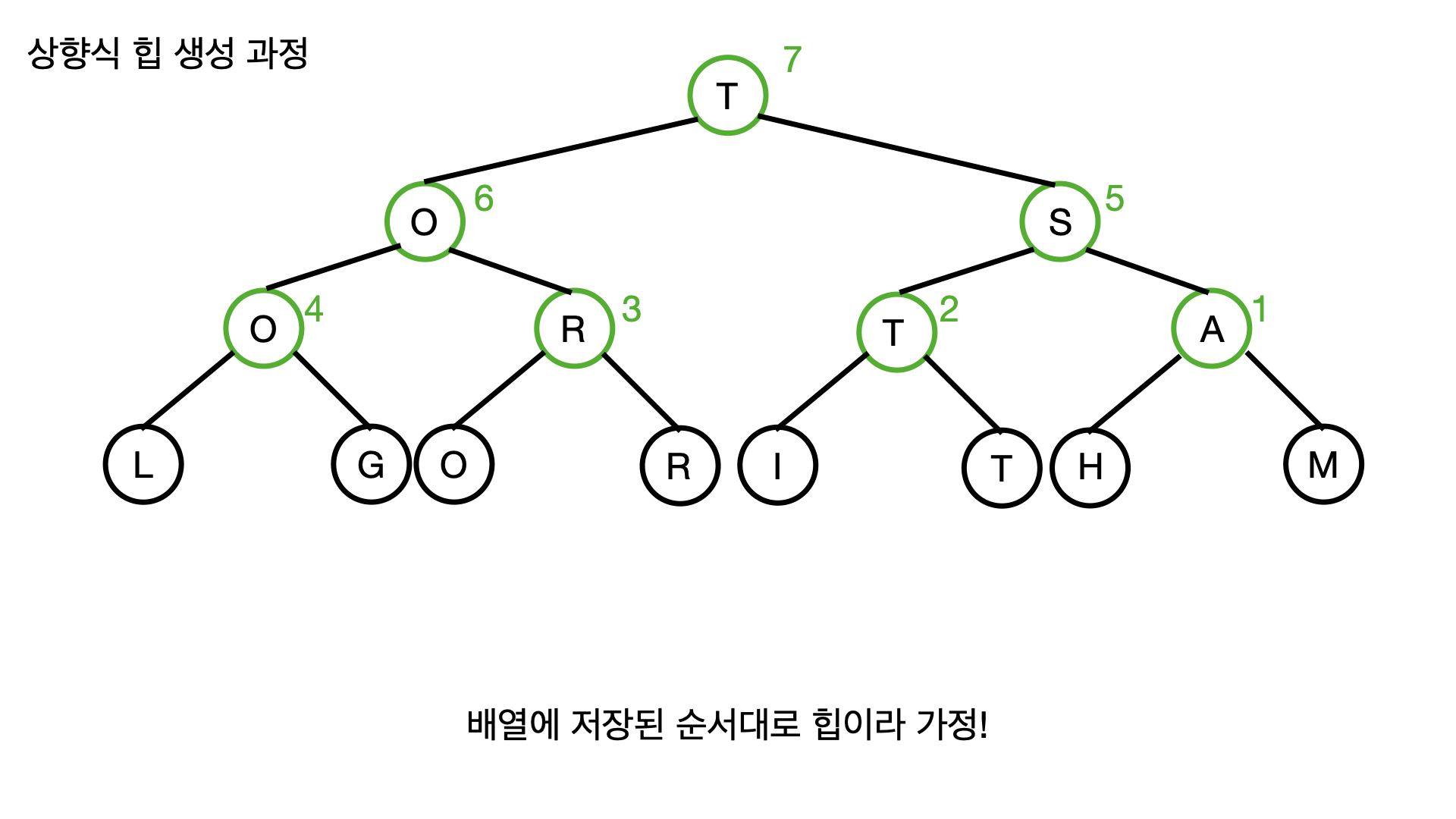
먼저 위 그림처럼 무작위 배열이 입력으로 들어왔다고 생각하자.
이 상태에서 초록색으로 표시한 노드들, 즉 내부 노드들에 한해서 가장 마지막인 내부 노드인 1번부터 뿌리인 7번까지 차례대로 DOWNHEAP 동작을 진행하면 우선순위에 맞게 힙이 졍렬되게 된다.
이후에 정렬된 힙을 뿌리에서 부터 차례대로 큰값을 빼주고 -> 대치하고 -> DOWNHEAP하고를 반복하면 정렬이 끝나게 된다.
이렇게 하게되면 하향식 힙 생성, 즉 힙의 길이가 0인 상태에서부터 값을 하나하나 채워나가 UPHEAP하는 과정이 없고, 동시에 UPHEAP을 이용하는것보다 범위도 절반으로 줄기때문에 속도가 더욱 빠르다.
(사실 당연하긴 하다, 이미 랜덤하게 들어온 값을 바로 정렬하는 것과, 값을 차례차례 우선순위에 맞게 채워넣고 정렬하는건 다르니까!)
void heap_sort2(int a[], int n) {
int k, t;
for(k = n/2; k >= 1; k--)
downheap(a, n, k);
while(n > 1) {
t = a[1];
a[1] = a[n];
a[n] = t;
downheap(a, --n, 1);
}
}위 코드를 보면 알 수 있듯이, 내부노드의 말단부터 뿌리 순서로 downheap을 진행한 다음, 뿌리노드를 빼고 -> 말단 노드를 뿌리로 열러서 다시 downheap을 진행하는 과정을 반복하게된다.
여기서 중요한 부분이 있다!!!
뿌리 노드를 1번, 즉 배열의 1번 index에 위치시키는 것으로 힙정렬을 구현했다.
근데 정렬해야할 배열의 경우는 0번 index 부터 값이 들어가 있게 된다.
따라서 이럴 경우는 위 정렬하는 함수의 index를 1번 노드가 뿌리가 아닌 0번 노드가 뿌리인것으로 수정해야 한다.
그게 아니라면 배열의 가장 앞부분에 빈 값을 추가해서 강제로 1번 인덱스부터 값이 있는 모양새로 만들어준다면 1번 노드가 뿌리 노드가 되게된다.
전체코드
//
// main.c
// Heap Sort
//
// Created by 박재현 on 2024/05/22.
//
#include <stdio.h>
#include <math.h>
#define INT_MAX 99999
#define HEAP_SIZE 100
void uphead(int a[], int k) {
int v = a[k];
a[0] = INT_MAX;
while(a[k/2] <= v) {
a[k] = a[k/2];
k /= 2;
}
a[k] = v;
}
void downheap(int a[], int n, int k) {
int i;
int v = a[k];
while(k <= n/2) {
i = k * 2;
if(a[i + 1] > a[i] && i < n)
i++;
if(v >= a[i])
break;
a[k] = a[i];
k = i;
}
a[k] = v;
}
void insert(int a[], int *n, int v) {
a[++(*n)] = v;
uphead(a, *n);
}
int extract(int a[], int *n) {
int v = a[1];
a[1] = a[(*n)--];
downheap(a, *n, 1);
return v;
}
void heap_sort(int a[], int n) {
int i;
int hn = 0;
for(i = 1; i <= n; i++)
insert(a, &hn, a[i]);
for(i = hn; i >= 1; i--)
a[i] = extract(a, &hn);
}
void heap_sort2(int a[], int n) {
int k, t;
for(k = n/2; k >= 1; k--)
downheap(a, n, k);
while(n > 1) {
t = a[1];
a[1] = a[n];
a[n] = t;
downheap(a, --n, 1);
}
}
void print_heap(int a[], int n) {
int cnt = 0;
int goal = 1;
int level = (int)sqrt(n) + 1;
for(int i = 1; i <= n; i++) {
cnt++;
for(int j = 0; j < level; j++)
printf(" ");
printf("%d", a[i]);
if(cnt == goal) {
printf("\n");
goal = cnt * 2;
cnt = 0;
level--;
}
}
printf("\n\n");
}
void print_array(int a[], int n) {
for(int i = 1; i <= n; i++) {
printf("%d ", a[i]);
}
printf("\n");
}
int main(int argc, const char * argv[]) {
int node = 0;
int heap[HEAP_SIZE];
int heap2[11] = {INT_MAX, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1};
for(int i = 1; i <= 10; i++) {
insert(heap, &node, i);
}
printf("Insert data into heap from 1 to 10\n");
print_heap(heap, node);
heap_sort(heap, node);
printf("After sorting\n");
print_heap(heap, node);
printf("Before sorting\n");
print_array(heap2, 10);
heap_sort2(heap2, 10);
printf("After sorting\n");
print_array(heap2, 10);
return 0;
}
실행 결과