재귀함수가 뭘까?!

위 짤은 스트리머 김찬호 형님의 레전드 영상 중 하나인 랄로와 기울어진 마라탕 영상의 일부분인데, 위 짤이 바로 재귀함수를 정확하게 표현해주고 있다고 생각한다.

???: 랄로 방송이 왜 재귀함수임!?

왜 위에 저 짤이 재귀함수를 표현해주냐고 생각하냐면 바로 스트리머 본인의 화면에서 ➡️ 또 다른 작은 화면으로 내 화면이 보이고 ➡️ 그 작은 화면에서 또 다시 다른 작은 화면으로 내 화면이 보이고

위와같은 현상이 계속 반복되는데 이 현상이 바로 재귀함수와 같다라는 생각이다!!

---

자기자신을 호출한다!

재귀 함수(Recursive Function)는 자기자신으로 부터 호출이되는 함수를 말하고, 이런 함수 호출을 재귀 호출(Recursion)이라고 한다.

그리고 재귀적으로 문제를 해결함은 또 문제를 점점 더 작은 단위로 쪼개면서 해결하는걸 의미한다.

만약 커다란 문제를 해결하기 위해서 솔루션을 마련하기 어려울수 있는데, 작은 문제는 해결 방법이 눈에 보일수 있기때문에 이런식으로 큰 문제를 작은문제로 쪼개면서 문제를 해결하는 방법이 재귀호출을 이용하는 방법이다.

재귀함수의 코드는 간결하기 짝이없는데, 이런 소스코드를 작성하기는 쉽지가 않다.
또 운좋게 "어!!? 이게 왜 됨!!?" 이렇게 코드를 작성했다고 하더라도 그 정확한 결과를 예측하기는 힘들다.

또 재귀 호출은 함수 호출을 위해서 내부 스택을 사용하는데 잘못된 재귀 호출은 시스템을 다운시킬수도 있어서 디버깅하기도 어려운 특성을 가지고 있다.

---

잘못된 재귀 호출

재귀적인 방법은 일상생활에서도 많이 접하는 방법이다.
내가 친구한테 "야 장미가 뭐냐??" 라고 물어봤더니 똑똑한 친구가 "장미는 장미다" 라고 이야기해줬다라고 해보자.

당연히 장미는 장미이기 때문에 이 명제는 참이다. 하지만 내가 장미에 대해 무엇을 알게되었지?? 라고 생각해보면 사실상 나의 문제 해결에 전혀 도움이 되지 않는다.

위 내용은 코드로 작성해보면 아래처럼 될거같다.

void rose(void) {
	rose();
}

자! 그러면 rose 함수의 실행 결과가 어떻게 될까??

아마도 무한루프일 것이라고 생각할 수 있지만 실제적으로는 함수의 호출시에는 시스템 내부의 스택에 복귀 주소와 인자를 저장해야 하므로 rose함수가 호출될때 마다 스택에 자료가 쌓여간다.

이러다 function call stack의 한계를 넘어가면 십중팔구 시스템이 죽어버리는 일이 일어난다.

오케이 그럼 다른 친구한테 "야 철이 집이 어디냐??" 라고 물어봤더니 친구가 "철이 집은 영희 집 옆이야." 라고 대답해줬다.

오? 그래도 철이집이 철이집이지~ 라고 대답안해서 낫배드다!

그럼 "영희 집은 어디냐??" 라고 물어봤더니 "영희 집은 철이 집 옆이다." 라고 대답했다.

그렇다면 철이와 영희가 서로 이웃이라는것만 알뿐, 정확히 어느 지역에 거주하는지 알 방법이 없다.

이런식의 재귀 호출을 간접 재귀 호출이라고 하고, 이런 예시 또한 잘못된 재귀 호출이라고 할 수 있다.

void cheol(void) {
	young();
}

void young(void) {
	cheol();
}

---

재귀 호출의 요건

또 다른 예를 한번 들어보자.

친구 집들이를 가려고 근처에 다른 사람에게 "아이파크 어떻게 가야하나요???" 라고 물어봤을때 "아..? 일단 저기 앞에 사거리 신호등에서 오른쪽으로 돌면 편의점이 있는데 거기서 다른분께 물어보실래요??" 라고 했다.

그래서 시킨대로 사거리 신호등에서 오른쪽으로 돌아서 편의점을 찾았고, 거기서 또 다른분께 "아이파크 가려면 어떻게 가야하나요??" 라고 물어봤더니 "저기 앞에 보이는 GS25 편의점 맞은편이 아이파크에요!" 라고 알려줬다.

덕분에 나는 친구가 살고있는 아이파크에 잘 도착할 수 있었다!

위 방법이 바로 재귀 호출을 사용해서 문제를 해결하는 방법이다.

1. 재귀 호출이 이루어질때마다 문제의 크기가 점점 작아져야 한다.
2. 재귀 호출이 끝나는 종료 조건이 명확하게 있어야 한다.

이 두가지를 절대 잊지말고 몇가지 예시를 한번 작성해보자!

---

누승을 구하는 재귀함수

누승이 뭐지? 처음 들으보는데? 하는 사람들이 있을수도 있는데 영어로 하면 Factorial 팩토리얼이다.

우선 누승은 어떻게 재귀적으로 정의되는지 알아보자!

N의 누승은 N!이라고 표시하고, N팩토리얼 이라고 말한다.

N! = N x (N-1) x (N-2) x ... x 2 x 1
= N x (N-1)!, When 0! = 1

위와 같이 재귀적으로 표현할수 있고, 0의 누승이 1이라고 정의하는것은 이부분이 바로 재귀 호출을 끝내는 종료조건이 되기 때문이다.

코드로 한번 작성해보자!

int foactorial(int n) {
	if(n == 0)
    	return 1;
    return n * factorial(n - 1);
}

생각보다 간단한데?? 라는걸 느낄 수 있는데, 4!를 계산할때 실제로 어떤식으로 동작하는지 한번 그려보자!

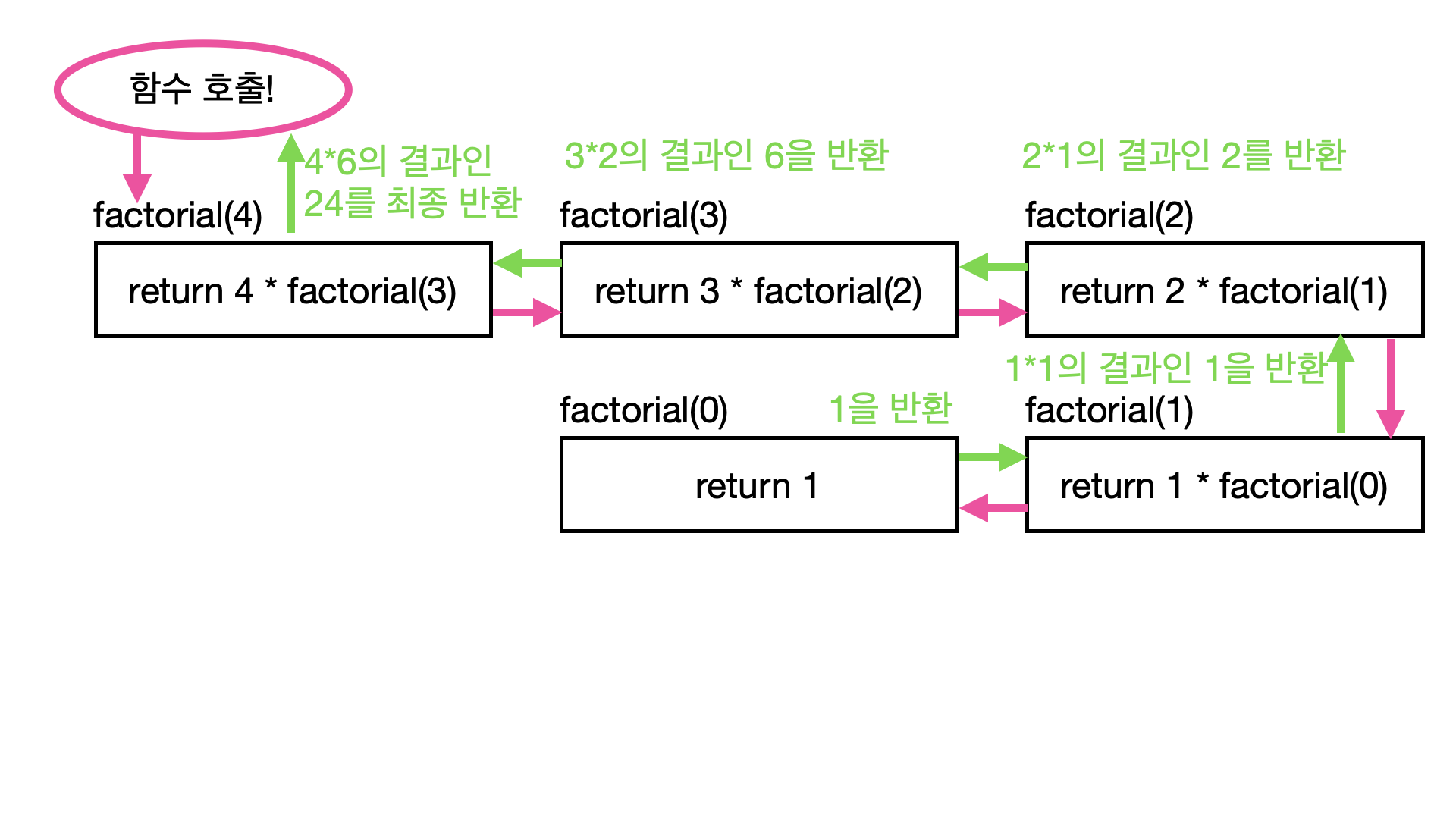
핑크색으로 표시한 화살표는 함수가 호출되는 순서이고, 초록색으로 표시해둔 화살표는 호출된 함수가 종료되는 순서이다.

---

피보나치 수열을 구하는 재귀함수

재귀 호출은 하나의 함수에서 한번만 이루어져야 하는것은 아니다.

하나의 함수에서 두번 혹은 그 이상도 자기자신을 호출할 수 있고, 자기 자신을 호출하는 횟수는 주어진 문제를 몇개로 나누어서 푸느냐에따라 결정된다.

예를들어서 피보나치 수열을 생각해보자.

F(N) = F(N-1) + F(N-2), 단, F(1) = F(2) = 1

즉 앞의 2개의 숫자를 더해서 새로운 값을 구하는게 피보나치 수열이고, 위 식을 통해서 보듯이 F(N)을 구하기 위해서는 F(N-1)과 F(N-2)를 알아야 한다는걸 알수있고 재귀호출을 2번 해야한다는것 또한 알 수 있다.

그러면 위 내용을 코드로 한번 작성해보자!

int fibonacci(int n) {
	if(n == 1 || n == 2)
    	return 1;
    return fibonacci(n - 1) + finonacci(n - 2);
}

위 함수가 수식으로 정의한것과 완전히 동일한 모양이라는걸 알 수 있는데, 이게 어떤식으로 동작하는지는 바로 이해가 힘들수있다.

그럼 어떤식으로 동작하는지도 한번 그려보자!

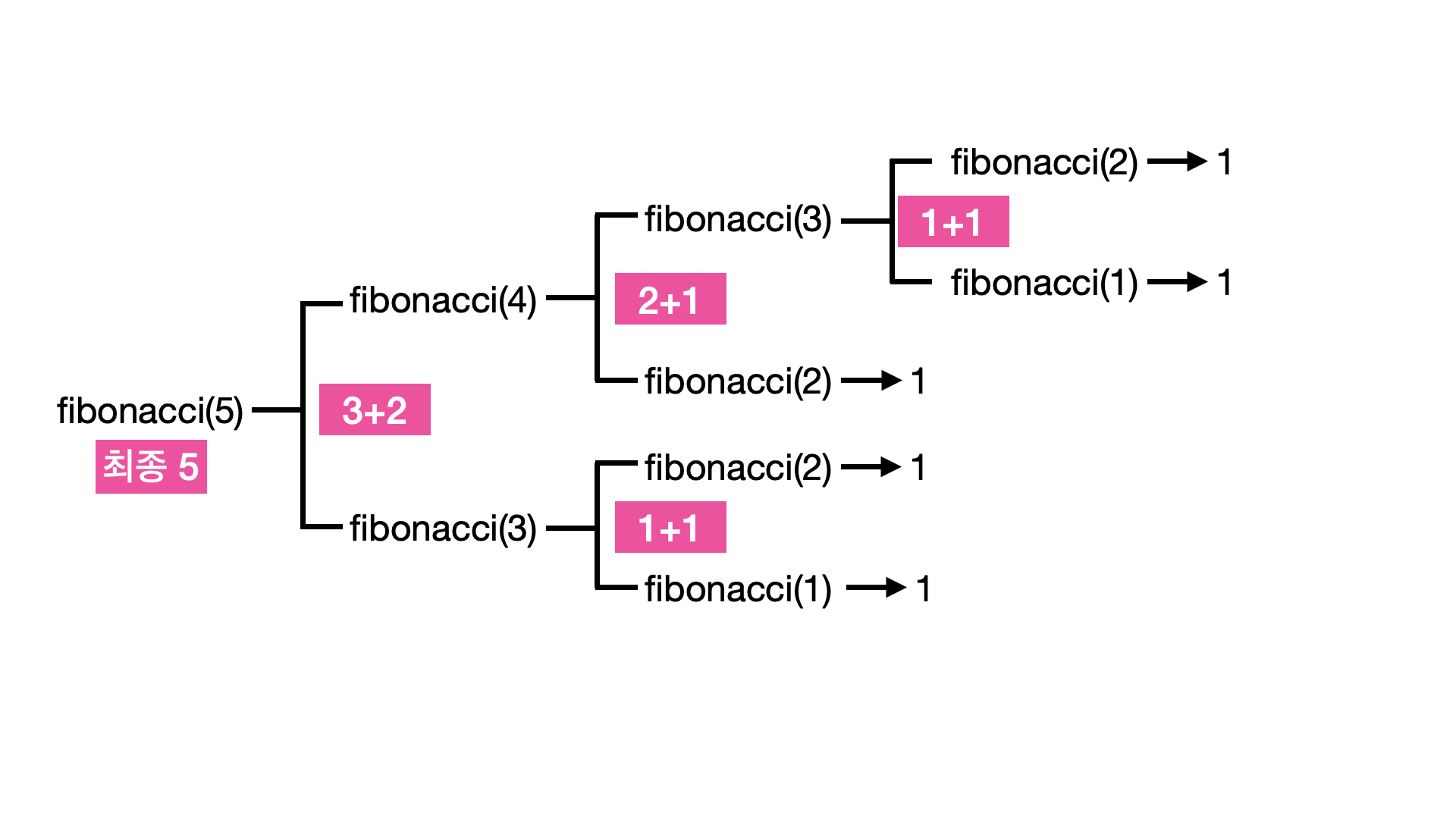
이런식으로 재귀나무를 직접 그려보면서 값을 유추해본다면 하나의 함수에서 두번씩 자기자신을 호출할지라도 큰 어려움없이 재귀함수의 동작을 분석할수 있다!

---

재귀 호출 전략

재귀 호출이 문제를 풀어가는 전략은 대략 3가지로 나눌수 있다.

1. 문제의 크기를 조금씩 줄여가는 방법

문제가 너무 커서 해결이 힘든 문제는 해결할 수 있는 단위까지 차례차례로 줄여서 해결한다. 이 유형의 예시로는 맨처음에 누승(팩토리얼)을 구하는 함수나 피보나치 수열, 하노이탐 문제도 이런 유형이다.

2. 문제의 크기를 양분하여 가는 방법

꼭 정확히 절반이 아니더라도 되는 경우가 있으며(퀵소트) 수학적으로 정확히 반을 나누어가는 경우도 있다.
여튼 이런 방법을 분할정복 혹은 분할통치 Divide and Concuer라는 방법이라고도 한다.

3. 문제 자체에 점근하여 가는 방법

Tree를 순회하는 방법이 가장 전형적인 예시다.
예를들어서 뿌리를 먼저 순회하는 전위순회(Preorder Travels)로 나무를 순회할때를 생각해보자.

먼저 뿌리를 방문하고, 왼쪽의 subtree를 방문해야 하는데 나무 자체를 방문할수는 없다.

오로지 개별 노드만 방문할 수 있는 단위가 되므로, 이때의 재귀 호출은 계속해서 왼쪽 작은 나무를 타고타고 내려가면서 가장 최자측의 노드를 찾아내는 것이 된다.

---

하노이의 탑

하노이탑이 뭐냐? 라고 물어볼수 있는데 그림으로 그려보면 아래와 같은게 바로 하노이탑이다.

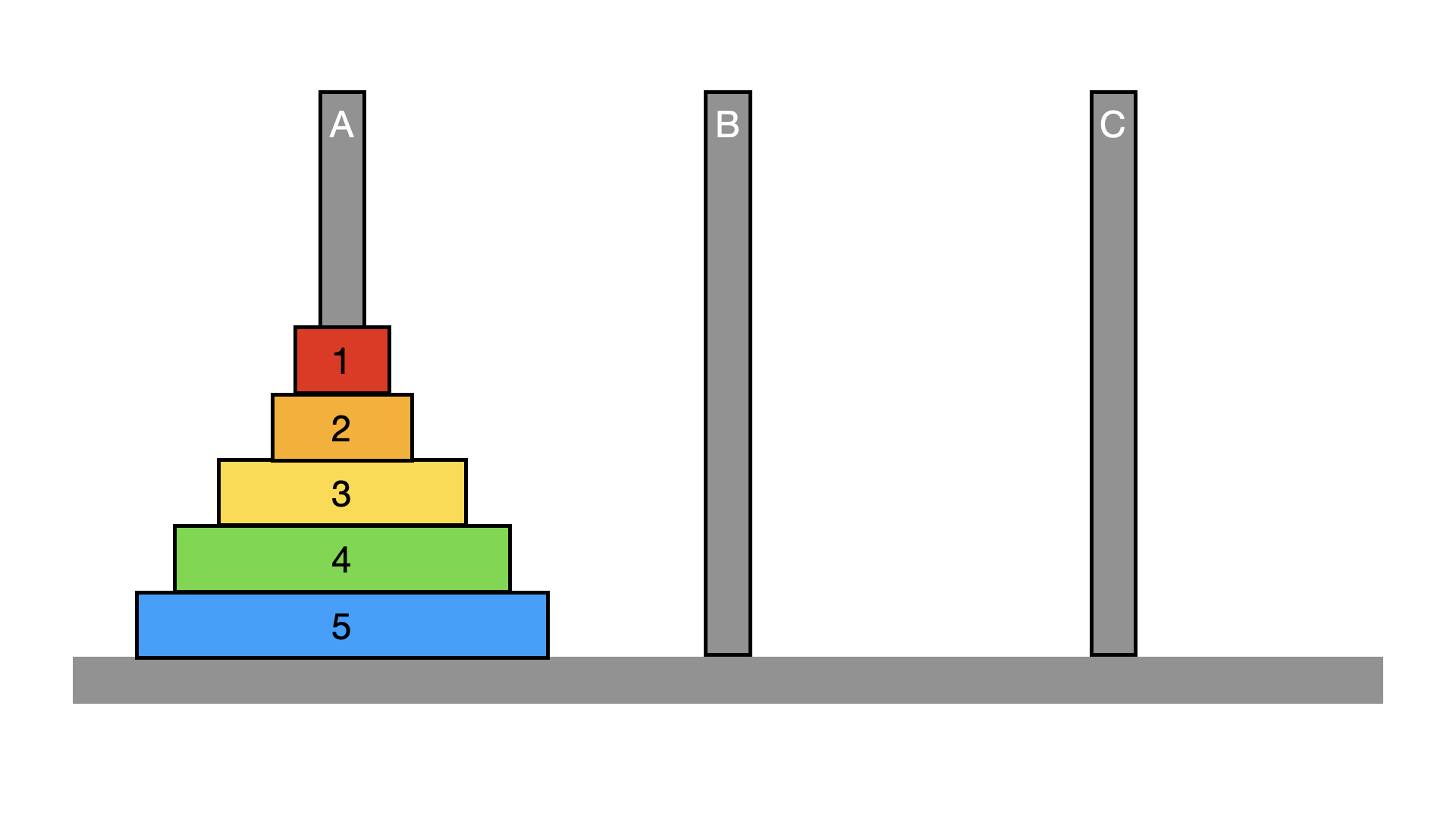
브라만 사원의 승려분들이 하셨다는게 하노이탑인데, 하노이탑은 3개의 기둥과 서로다른 크기인 N개의 원판으로 구성된다.

이 원판들은 세개의 기둥 중 하나에 반드시 꽂혀 있어야 하고, 자신보다 작은 원판 위에는 올라갈 수 없다.

즉 위 그림에서 1번 원판위에 2번 원판이 올라올 수 없고, 3번 원판위에 4번, 5번 원판이 올라갈 수 없다는 소리다.

문제는 1번(A) 기둥에 N개의 원판이 모두 꽂혀져 있는 상태에서 시작된다. 물론 원판은 크기의 순서대로 꽂혀있는 상태이고, 이 원판을 2번(B) 기둥을 이용해서 3번(C) 기둥으로 모두 옮기는 것이다.

이 과정에서 원판을 옮길때 나보다 작은 원판 위에 올라갈수 없다는 규칙은 여전히 유효하다.

그렇다면 문제를 가장 잘 이해하는 방법은 뭘까!!?

바로 적은수의 원판으로 직접 문제를 풀어보면 된다 ㅋㅋㅋ

원판이 3개가 있다고 가정할때, 위의 규칙대로 3개의 원판을 A기둥에서 C번기둥으로 옮기는 과정을 직접 해보자.

1. A기둥에서 1번 원판을 C기둥으로 옮긴다.
2. A기둥에서 2번 원판을 B기둥으로 옮긴다.
3. C기둥에서 1번 원판을 B기둥으로 옮긴다.
4. A기둥에서 3번 원판을 C기둥으로 옮긴다.
5. B기둥에서 1번 원판을 A기둥으로 옮긴다.
6. B기둥에서 2번 원판을 C기둥으로 옮긴다.
7. A기둥에서 1번 원판을 C기둥으로 옮긴다.

위 과정에서 하노이탑을 해결하기 위해서 반복적이고 공통된 규칙을 찾아야 한다.

1. A기둥에서 N-1개의 원판을 기둥B로 옮긴다.
2. A기둥에서 1개(가장 큰) 원판을 기둥C로 옮긴다.
3. B기둥에서 N-1개의 원판을 기둥C로 옮긴다.

위와 같이 설명하면 매우 간단한데, 코끼리를 냉장고에 집어넣는 방법처럼 황당한데, 어떻게 N-1개의 원판을 동시에 옮길수 있을까??

사실 N-1개의 원판을 동시에 옮긴다는 것이 아니고, 이 부분이 바로 재귀적인 표현임을 이해하면 위 알고리즘이 납득이 된다.

알고리즘의 1번을 잘 보면, 기둥 A에서 N-1개의 원판을 기둥B로 옮기는 방법을 새로운 문제로 생각하고 다시 알고리즘을 적용해 보자.

그럼 기둥 A에서 N-2개의 원판을 기둥C로 옮겼다가, 기둥A에서 1개의 원판을 기둥B로 옮기고 기둥C에서 N-2개의 원판을 기둥B로 옮기면 될거같다.

이런식으로 N-1개의 원판을 움직이는 문제에서 N-2개를 움직이는 문제로 점점 문제의 크기를 줄여가다 보면 1개의 원판을 움직이는 기본적인 문제에 도달하게 된다.

void move_disk(int from, int to) {
    printf("Move disk from %d pillar to %d pillar\n", from, to);
}

void hanoi(int disk, int from, int via, int to) {
    if(disk == 1) {
        move_disk(from, to);
    } else {
        hanoi(disk - 1, from, to, via);
        move_disk(from, to);
        hanoi(disk - 1, via, from, to);
    }
}

그림으로 함수가 실행되는 순서를 그려보면 아래와 같다.

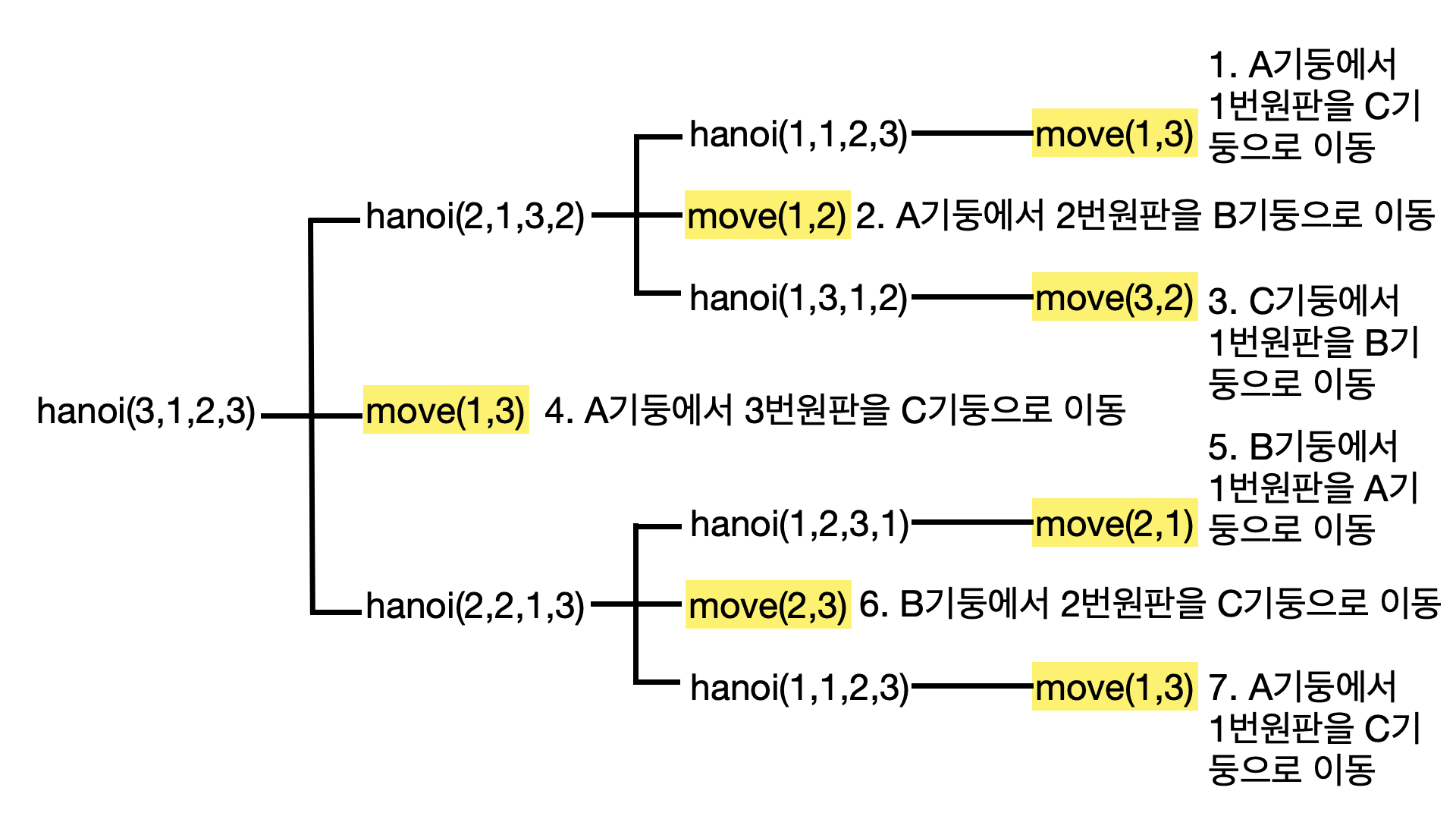
그림그리기 참 힘들다...