바로 이전글에서 C언어로 재귀함수에 대해서 살펴봤다.
그래서 이번에는 재귀함수로 조합과 순열을 구하는 함수를 작성해보려고 한다.
일단 이번에는 C언어 대신 Javascript를 사용해서 구현을 할것이고, 이유는 C언어로 하게되면 list를 또 구현하기 귀찮기 때문이다.
중요한건 어떤 프로그래밍 언어로 구현을 했느냐보다, 어떤 아이디어를 근거로 구현을 했는지 이해하는게 더 중요한게 아닐까 라는 생각을한다.
아! 그리고 개인적으로 재귀함수를 작성할때 중요하게 생각하는 부분이 바로 "앞으로 어떤식으로 전개될지를 고려하지 않는다." 이다.
뭔소리인가 싶겠지만, 정상적으로 재귀함수를 잘 만들었다면, 알아서 잘 돌아간다.
즉, "어... 이 다음에 이렇게 호출되서 이렇게 동작하고 그다음은 이렇게 되겠지...??" 이런걸 생각하지 않는다는 의미다.
따라서 패턴을 찾고 규칙을 만드는데에 더 신경을 써야한다고 나는 생각한다.
여튼 한번 만들어보자!
조합
조합이 뭘까?
일단 뭐 고등학교 수학시간에 배웠느니, 10개중에서 5개를 조합할때 나오는 경우의수가 몇개인데 이걸 어떤식으로 구하느니 이런건 다 스킵하겠다.
왜냐면 지금 중요한건 구현 하는거니까?
여튼 그러면 조합이 뭘까???
조합은 서로다른 N개의 아이템들 중에서 순서를 생각하지 않고 X개를 선택하는걸 말하는데, 이때 중요한건 조합의 순서는 상관 없다.
즉, [A, B]와 [B, A]는 같다는 소리다.
그럼 예시를 들어보자!
[1, 2, 3, 4] 4개의 숫자들 중에서 3개를 뽑아서 만들수 있는 조합을 손으로 직접 노트에 구해보자!
아마 정상적으로 조합을 잘 했다면, [ 1, 2, 3 ], [ 1, 2, 4 ], [ 1, 3, 4 ], [ 2, 3, 4 ] 이런 조합이 나온다.
오케이 그러면 [1, 2, 3]의 경우를 확인해보자!?
먼저 처음으로 1을 선택한다. 그 다음으로 남은 2, 3, 4 중에서 또 2를 선택한다, 그리고 또 남은 3, 4중에서 3을 선택하면되네??
오? 그러면 "현재 나 자신은 무조건 포함 시키고 나머지 아이템들에서 제외" + "조합해야할 갯수가 아직 모자라면, 여기서도 차례대로 바로 앞에부터 추가" 이런 규칙이 보이나??
다음으로 재귀함수의 종료조건은 어떻게 될까??
이 부분도 잘 생각해보면 간단한데, 조합할 숫자를 더이상 찾을 필요가 없을때가 종료조건일 것이고 아마도 조합해야할 숫자가 1일때일거다.
그러면 [1, 2, 3, 4] 4개의 숫자중 1개를 뽑아서 만들수 있는 조합은 바로 [1], [2], [3], [4]가 된다.
정리해보자!
- 재귀함수의 종료조건은 선택 해야할 숫자가 1일때 종료해야 한다.
- N개의 아이템들은 차례대로 무조건 자기자신이 포함되어야 한다.
- 남아있는 아이템들의 목록에는 이미 확인한 숫자는 포함하지 않는다.
- 선택해야할 숫자가 1보다 크다면 계속 반복하고, 반복될때마다 선택해야할 숫자는 1씩 감소한다.
위 내용응 자바스크립트 코드로 작성하면 아래처럼 작성할 수 있다.
function combinations(items, set) {
if(set === 1) {
return items.map(item => [item]);
}
let result = [];
items.forEach((item, index) => {
let left = items.slice(index + 1);
let combination = combinations(left, set - 1);
combination.forEach(comb => result.push([item, ...comb]))
})
return result;
}순열
순열을 조합하고 큰 차이가 없다, 다만 조합은 순서에 상관이 없었다면 순열은 순서에 상관이 있다. 그러니까 순열이겠지?
무슨말이냐?
조합의 경우는 [A, B]와 [B, A]는 서로 같은거라고 했지만, 순열의 경우는 위 경우는 서로 다른 경우다.
그렇다면 [1, 2, 3, 4] 이 4개의 숫자중에 3개를 뽑아서 순열을 한번 직접 손으로 구해보자!
전부 다 구하는건 어려움이 있으니 규칙이 보일때 까지만 해도 충분할것 같기한데, 중요한건 [1, 2, 3]과 [1, 3, 2]는 다르다 라는것이다.
일단 손으로 한번 찾아보자.
- 1을 선택하면 2, 3, 4가 남는다. => 1
- 여기서 2를 선택하면 3, 4가 남는다. => 1, 2
- 여기서 3을 선택하면 4가 남고 끝난다. => 1, 2, 3
그러면 1, 3, 2의 경우는 어떨까?
- 1을 선택하면 2, 3, 4가 남는다. => 1
- 여기서 3을 선택하면 2, 4가 남는다. => 1, 3
- 여기서 2를 선택하면 4가 남고 끝난다. => 1, 3, 2
여기서 규칙이 보일지 모르겠지만, 조합의 경우는 앞에서부터 순서대로 1개씩 빼면서 오고 뺀 숫자들은 앞으로 빠질 아이템들에서 제외된다.
근데 순열은 앞에서부터 순서대로 온다고 한들, 바로 직전에 선택된 숫자만 앞으로 빠질 아이템들에서 제외된다.
이해가 잘 안된다면 1, 2, 3과 2, 1, 3의 경우를 다시한번 해볼까?
[2, 1, 3]을 생각해보자, 맨 처음에 1, 2, 3, 4중에서 2를 선택하면 남겨진 목록은 1, 3, 4가 되어야 한다는거다 3, 4가 아니라.
조합이라면 1, 2, 3, 4 앞에서부터 차례대로 오면서 이미 2라는 값이 맨첫번째로 선택이 될때에는 1이라는 값은 선택지에서 아예 없어졌을거다.
따라서 순열의 경우 "방금 선택된 나 자신"만 제외하면 앞으로 선택할 목록이 된다.
그렇다면 종료조건은 어떻게될까?? 조합과 동일하다.
[1, 2, 3, 4] 중에서 1개의 숫자로 순열을 만들라면 [1][2] [3][4]가 될거다.
정리하면
- 종료조건은 선택해야할 숫자가 1일때이다.
- 조합과 다르게 선택해야할 목록은 초기상태에서 나 자신만 제외하면 된다.
- 재귀함수가 진행될수록 뽑아야할 숫자는 1씩 감소한다.
이걸 코드로 작성하면 아래와 같이 나온다.
function permutations(items, set) {
if(set === 1) {
return items.map(item => [item]);
}
let result = [];
items.forEach((item, index) => {
let left = [...items.slice(0, index), ...items.slice(index + 1)];
let permutation = permutations(left, set - 1);
permutation.forEach((per) => result.push([item, ...per]));
})
return result;
}설명이 이해가 가지않고 부족했다고 느낄지 모르겠지만, 노트에 손으로 직접 생각하면서 조합과 순열을 만들다보면 "오?? 이런 규칙이!?" 하면서 보이리라고 믿는다...!
전체 코드
function combinations(items, set) {
if(set === 1) {
return items.map(item => [item]);
}
let result = [];
items.forEach((item, index) => {
let left = items.slice(index + 1);
let combination = combinations(left, set - 1);
combination.forEach(comb => result.push([item, ...comb]))
})
return result;
}
function permutations(items, set) {
if(set === 1) {
return items.map(item => [item]);
}
let result = [];
items.forEach((item, index) => {
let left = [...items.slice(0, index), ...items.slice(index + 1)];
let permutation = permutations(left, set - 1);
permutation.forEach((per) => result.push([item, ...per]));
})
return result;
}
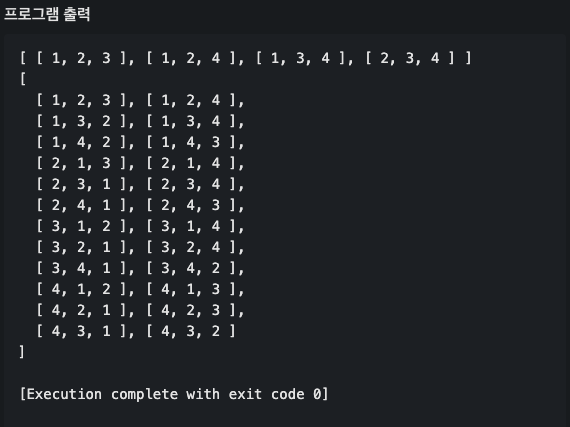
console.log(combinations([1,2,3,4], 3));
console.log(permutations([1,2,3,4], 3));실행결과