[9/14] 퍼셉트론

박정훈·2021년 9월 17일

ML numpy 과외 퍼셉트론

수업 일지

목록 보기

4/4

참고

프로그래밍 수업 내용 정리와 복습, 기초적인 딥러닝 정보 저장을 위해 작성합니다
고등학교 수학 정도의 지식을 가지고 있는 학생이 주된 대상입니다
Python에 대해서는 기본적인 내용(자료형, 제어문, 함수, 클래스)에 대한 학습을 마친 상태입니다

수업 환경

MacOS (학생) / Ubuntu 20.04 (선생님)
python 3.8
anaconda 4.10.3

인공신경망 스케치

인공신경망?

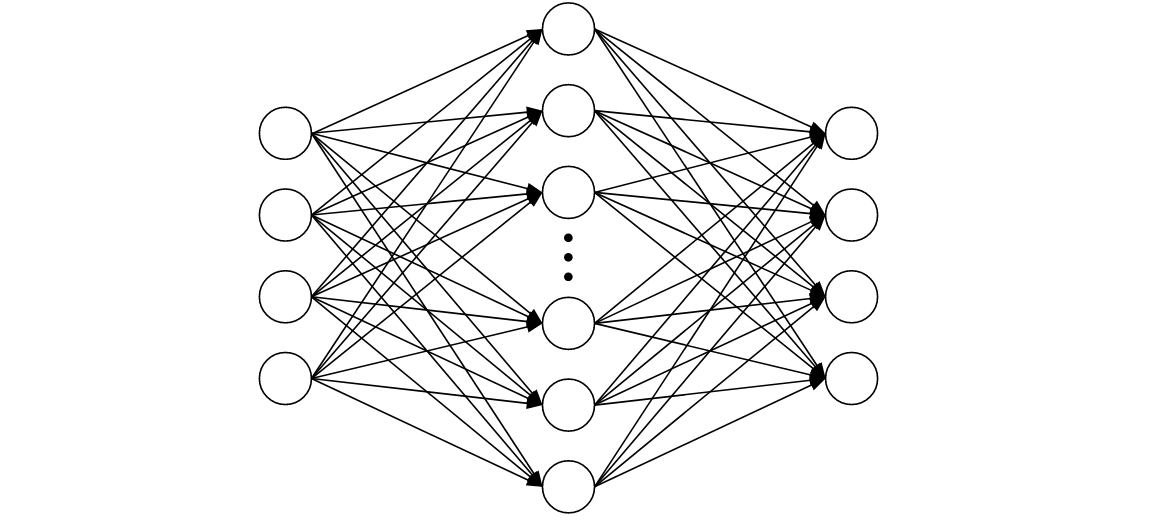
아래와 같은 그림을 보신 적이 있나요? 사실 정확히는 모르더라도, 원과 선이 아래 그림처럼 엉켜있는 그림은 꽤 익숙할지도 모릅니다. 인공신경망이라는 단어는 어떤가요? 이젠 알파고도 꽤 옛날 일이 되어버렸지만, 아무튼 인공신경망은 생각보다 익숙한 단어입니다.

오늘은 인공신경망이 어떻게 이루어지는지 매우매우매우 간단히 알아보고, 인공신경망을 이루는 가장 작은 단위라고 할 수 있는 퍼셉트론에 대해 배워볼 것입니다.

인공신경망 vs 신경망

인공신경망은 말 그대로 뇌 속에 있는 신경망을 인공적으로 모방한 구조를 가지고 있습니다. 신경계를 구성하는 신경 세포(뉴런)은 아래와 같이 생겼습니다. 가지돌기(머리 같이 생긴 부분)에서 다른 뉴런들로부터 신호를 받아들여, 축삭(꼬리 부분)에서 신호를 내보냅니다.

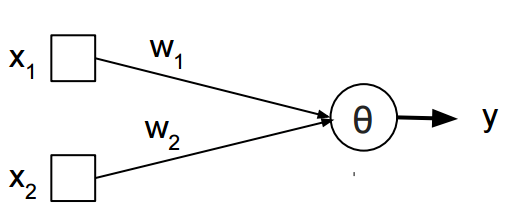
이번엔 퍼셉트론을 볼까요? 간단히 말해서 인공신경망에서 뉴런의 역할을 하는 친구입니다. x1, x2가 다른 퍼셉트론으로부터 온 신호라고 생각하고, y를 퍼셉트론의 출력이라고 생각하면, 뉴런과 비슷하지 않나요?

뉴런	퍼셉트론(인공신경망의 뉴런)

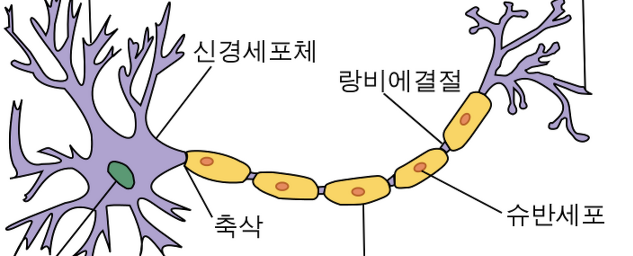뉴런이 다른 뉴런으로부터 신호를 받아 적절히 처리한 후 다른 뉴런으로 내보냅니다. 퍼셉트론 역시 마찬가지로, 다른 퍼셉트론으로부터 신호를 받아 내부에서 연산한 후 값을 내보냅니다. 위의 x1, x2를 다른 퍼셉트론으로부터 받은 신호, y를 다른 퍼셉트론에게 보낼 신호라고 생각하면 됩니다.

이런 방식으로 퍼셉트론들이 서로 연결되고, 가장 위에서 본 익숙한 인공신경망이 구성되는 것이죠! layer라는 친구는 아직 배우진 않았지만, 퍼셉트론들을 계층별로 분류해놓았다고 생각하면 됩니다.

인공신경망의 학습

인공신경망의 학습은 사실 자세히 보면 쉽지만은 않습니다. 하지만 개념 정도는 이해할 수 있죠! 인공신경망이 신경계를 모방했듯이, 인공신경망의 학습도 인간의 학습을 어느정도 모방했습니다.

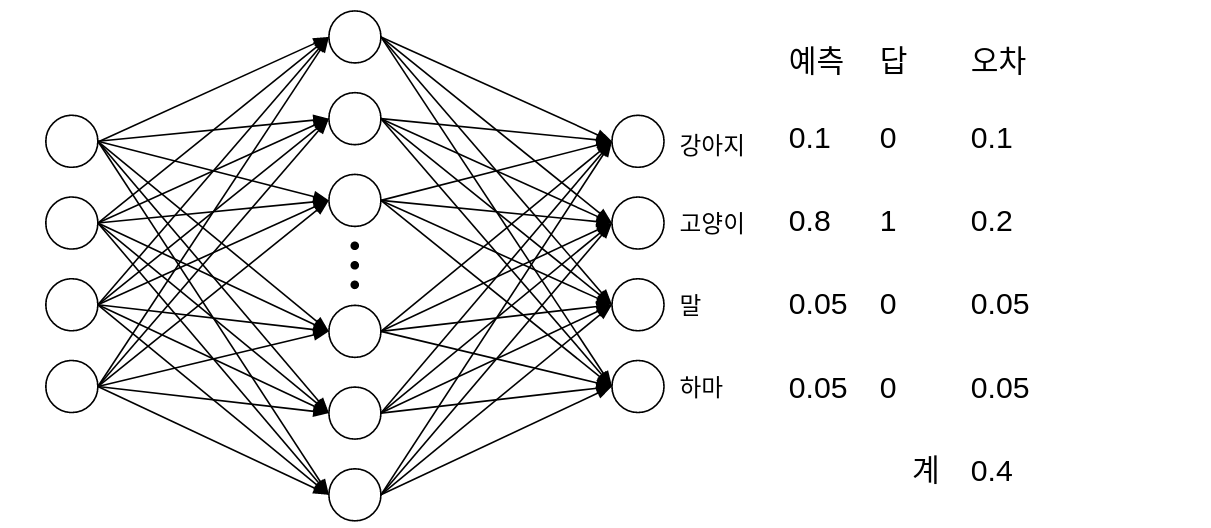
사람이 어떤 문제를 풀 때, 열심히 푼 후 정답을 확인합니다. 인공신경망도 마찬가지입니다. 어떤 입력이 입력되었을 때 신경망은 출력을 내보내는데, 이 출력을 정답과 비교합니다. 이미지 분류로 예를 들면, 입력(ex. 고양이 이미지)이 들어오면 인공신경망은 이 이미지가 어떤 동물인지 예측합니다. 인공신경망이 잘 예측하면(출력 = "고양이") ok, 예측하지 못하면(ex. 출력 = "강아지") 패널티를 주는 것이죠.

퍼셉트론

퍼셉트론 정의

퍼셉트론은 사실 별게 없습니다. 이전에 말한대로 여러 개의 신호를 입력으로 받아, 하나의 신호를 출력하는 장치입니다. 인공신경망의 가장 간단한 구조로, 신경망의 흐름을 만들어주죠. 언제 어떤 신호를 출력하느냐는 입력값에 영향을 받습니다. 아래 그림은 입력 값이 2개인 간단한 퍼셉트론입니다.

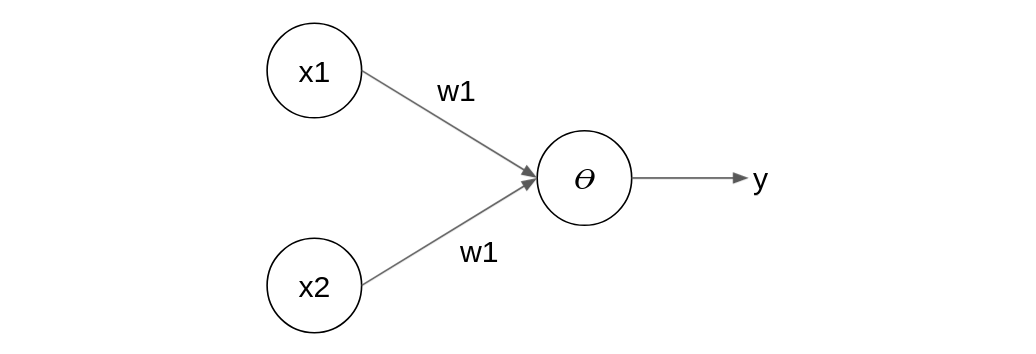
x1과 x2는 입력, y는 출력입니다. w1과 w2는 가중치로, 각 입력이 출력에 미치는 영향을 의미합니다. θ는 임계값으로, 신호의 총합(입력 * 가중치의 총합)이 이 임계값을 넘어야 퍼셉트론이 활성화됩니다(즉, y가 1). 활성화되지 않으면 y는 0입니다.

y= \begin{cases} 0, & (w_1 x_1 + w_2 x_2 \le \theta) \\ 1 & (w_1 x_1 + w_2 x_2 \gt \theta) \end{cases}

즉 퍼셉트론을 결정하는 것은 w1과 w2 등의 가중치, 그리고 임계값 θ입니다. 같은 가중치와 임계값을 가지면 같은 퍼셉트론이죠. 우리는 편의를 위해 θ를 -b로 쓴 후 이항하여 0과 비교하겠습니다. 식으로 나타내면 다음과 같습니다. b를 우리는 편향(bias)이라고 부르겠습니다.

y= \begin{cases} 0, & (w_1 x_1 + w_2 x_2 + b\le 0) \\ 1 & (w_1 x_1 + w_2 x_2 + b \gt 0) \end{cases}

동일한 동작을 수행하는 퍼셉트론은 여러 개가 있을 수 있습니다. 논리 게이트에서 더 자세히 보죠.

논리게이트

논리게이트는 이미 알고있을 수도 있습니다. 2개의 입력(0 or 1)에 따라 1개의 출력을 내보냅니다. 다양한 종류의 논리 게이트가 있으니, 진리 표로 확인해봅시다.

x1	x2	출력	AND	OR	NOT(x1)	NAND	NOR	XOR	XNOR
0	0	→	0	0	1	1	1	0	1
0	1	→	0	1	1	1	0	1	0
1	0	→	0	1	0	1	0	1	0
1	1	→	1	1	0	0	0	0	1

뭐가 많아 보이지만 간단합니다.

AND는 입력이 모두 1일 때만 1, OR은 입력이 하나라도 1이면 1입니다. NOT은 특이하게 입력을 1개만 받는데요, 입력이 0이면 1, 1이면 0을 반환합니다. NAND와 NOR은 각각 AND와 OR에 NOT을 붙인 것입니다.

XOR은 exclusive or의 약자로, OR과 비슷하지만 입력이 모두 1일 때는 0입니다. 다르게 말하면, 입력이 서로 다를 때 1을 갖습니다. XNOR역시 XOR에 NOT을 붙인 것으로, 입력이 서로 같을 때 1입니다.

퍼셉트론으로 AND, OR, NOT 만들기

논리 게이트는 2개의 입력을 받고 1개의 출력을 내보내죠(입력이 2개 이상인 게이트도 존재합니다). 여러 개의 입력을 받고 하나의 출력을 내보낸다는 점에서 논리 게이트를 퍼셉트론으로 구현할 수 있습니다. 입력이 0 또는 1이 들어올 때 적절한 가중치와 편향을 골라 원하는 출력을 내보내도록 설계하면 됩니다.

AND/NAND gate

코드가 길지 않으니 코드부터 보겠습니다.

def AND(x1, x2):
    X = np.array([x1, x2])
    W = np.array([1, 1])
    b = -1.5
    tmp = sum(X * W) + b
    return 0 if tmp <= 0 else 1

$w_1 x_1 + w_2 x_2$ 라는 식은 numpy array를 통해서 간단히 구할 수 있습니다. array의 *연산은 원소 별로 곱하는 것이었죠. 곱한 결과를 sum함수를 통해 더해주면 원하는 식이 나옵니다.

여기에선 w1과 w2를 모두 1로, b는 -1.5로 지정했네요. 아래와 같이 확인해보면 AND게이트와 동일한 결과를 보여주는 것을 확인할 수 있습니다.

for i in range(2):
    for j in range(2):
        print(AND(i, j))
# 0 0 0 1

NAND 게이트는 AND게이트에 NOT만 붙여준 것입니다. 따라서 AND게이트 코드의 W와 b에 -1만 곱해주면 NAND게이트로 작동하게 됩니다. 나중에 NOT게이트를 구현하게 되면 NAND2()와 같이 만들 수도 있겠네요.

def NAND(x1, x2):
    X = np.array([x1, x2])
    W = np.array([-1, -1])
    b = 1.5
    tmp = sum(X * W) + b
    return 0 if tmp <= 0 else 1
    
def NAND2(x1, x2):
    return NOT(AND(x1, x2))

Note: 퍼셉트론은 직선으로 영역을 나눈다
처음 AND를 만들 때 W와 b에 적절한 값을 찾기 쉽지 않았을 것입니다. 이때 퍼셉트론을 조금 다르게 해석하면 값을 찾는 것이 한결 쉬워집니다.

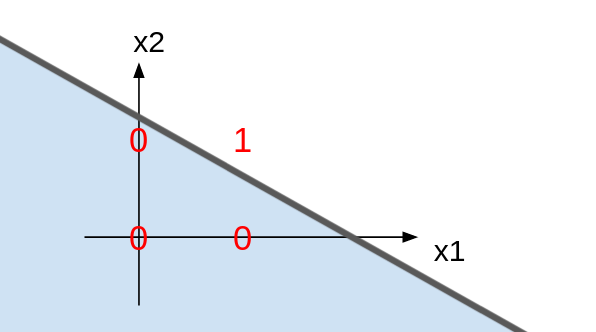
사실 퍼셉트론은 $w_1 x_1 + w_2 x_2 + b = 0$ 이라는 직선을 긋고, 이 직선보다 아래 부분은 0으로, 위쪽 부분은 1로 구분하는 장치입니다. 그래서 우리는 퍼셉트론을 linear classifier(선형 분류기)라고도 부릅니다. 논리 게이트는 어차피 입력이 0 아니면 1이기 때문에 2차원 평면을 두 부분으로 나눠도 충분했던 것이죠. NAND는 직선은 그대로 둔 채 영역 구분만 반대로 해주면 되기 때문에 -1을 곱해준 것입니다.

그럼 직선의 기울기(w1과 w2), 그리고 절편(b)만 골라주면 AND게이트를 만들 수 있겠죠? 위 예제에선 가중치들이 서로 같았지만, 아래 그림처럼 굳이 같을 필요는 없습니다. 구분만 잘 하면 되니까요!

OR/NOR gate

OR과 NOR역시 퍼셉트론이 linear classifier라는 점을 알았으면 어렵지 않게 W와 b를 찾아내 구현할 수 있습니다. 저 같은 경우 W = [1, 1], b = -0.5로 구현했네요.

NOT gate

NOT 게이트는 입력이 하나입니다. 사실 0 or 1을 1 or 0으로 바꿔주기만 하면 되기에 구현이 간단하지만, 이미 구현한 퍼셉트론을 이용해서 만들어보았습니다.

def NOT(x):
    return NAND(x, x)

NAND는 NOT + AND로, 입력이 모두 1일 때만 0이었죠. NAND의 두 입력에 같은 x를 주게 되면, (0, 0) 또는 (1, 1)만 NAND의 입력으로 들어오게 됩니다. 위의 게이트 진리표에서 확인하면, 결국 NOT과 동일하게 동작하는 것을 볼 수 있습니다.

다층 퍼셉트론으로 XOR 만들기

그럼 XOR은 어떻게 구현할까요? 퍼셉트론이 linear classifier라는 것을 배웠으므로, 좌표 평면에서 XOR에 대응되는 직선을 그려봅시다.

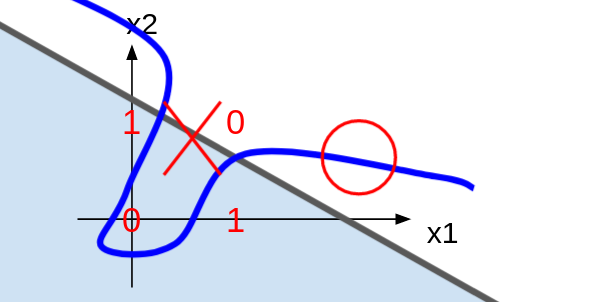
그런데 XOR은 그 어떤 직선으로도 분류할 수 없습니다. AND나 OR이 하나의 직선으로 잘 분류되던 것과는 상반되는 결과입니다. 이게 바로 퍼셉트론의 한계입니다. 하나의 퍼셉트론으로는 선형적인 분류밖에 할 수 없었던 것이죠. XOR을 분류하려면 비선형적인 경계(곡선)을 그려야합니다. 이를 위해 퍼셉트론들을 연결하기 시작합니다.

게이트를 조합하여 XOR 만들기

AND, OR, NOT 등의 게이트를 조합해서 XOR과 동일한 동작을 하는 모델을 만들 수 있다면, 결국 XOR을 퍼셉트론을 연결시켜 만든 셈이 됩니다. 각각의 게이트들을 이미 퍼셉트론으로 구현해놨기 때문이죠.

XOR이 입력이 서로 다를 때 1을 갖는다는 점에 주목해봅시다. x이라는 표현을 x = 1, x'이라는 표현을 x = 0이라고 약속하죠. 그럼 XOR은 다음과 같이 표현할 수 있습니다.

XOR(x1, x2) = (x1 AND x2') OR (x1' AND x2)

입력이 서로 다를 때라는 표현을 반영했습니다. x1이 1이면 x2는 0, 또는 그 반대일 때 XOR의 결과가 1이 되는 것이죠.

XOR 구현

위에 등장한 XOR 식을 구현하면 다음과 같습니다.

def XOR(x1, x2):
    not_x1 = NOT(x1)
    not_x2 = NOT(x2)
    tmp1 = AND(x1, not_x2)
    tmp2 = AND(not_x1, x2)
    return OR(tmp1, tmp2)

모든 입력에 대해 테스트해보면 XOR의 진리표와 동일하게 작동하는 것을 볼 수 있습니다. 그런데 이게 어떻게 퍼셉트론을 연결한 것이냐구요? 그림으로 보면 아래와 같습니다. 방금 3층으로 구성된 신경망을 만든 셈이죠!

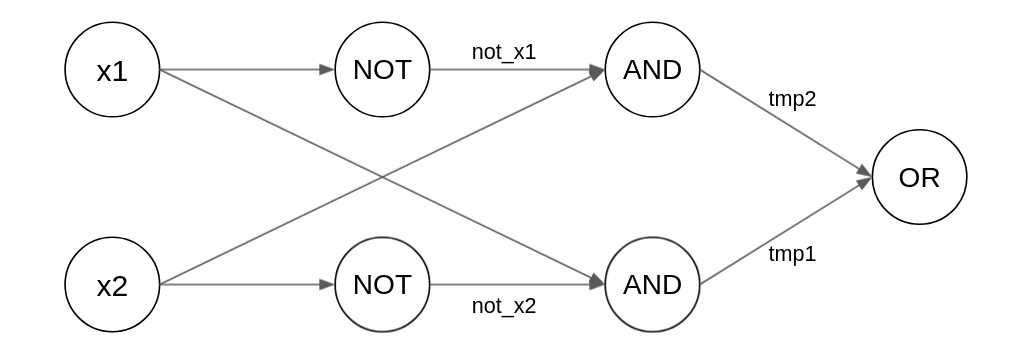
앞으로 배울 인공신경망도, 연산의 형태는 조금 변할 수 있지만, 본질적으론 오늘 한 XOR 만들기와 다르지 않습니다. 각 퍼셉트론의 결과들을 다음 퍼셉트론으로 내보내는 것이죠. 이러한 과정을 통해 비선형적인 경계를 만들어, 퍼셉트론을 1개만 사용했을 때 나타나는 한계를 극복하는 것입니다.

논리 게이트 심화

오늘 배운 논리 게이트들로 사실 (이론상) 컴퓨터도 만들 수 있습니다. 결국 컴퓨터도 수많은 논리 게이트들의 집합이랍니다.

사실, NAND 게이트 만으로도 모든 것을 만들 수 있습니다. NOT은 오늘 NAND를 통해 구현했죠. AND는 NOT(NAND(x1, x2))의 방식으로 구현할 수 있습니다. 이와 비슷하게 OR, NOR, XOR, XNOR역시 모두 NAND만을 이용해 구현할 수 있습니다.

믿기지 않는 친구를 위해, 남은 수업 시간 동안 이진수에 대해 간단히 배워보고, 오늘 만든 논리 게이트들로 이진수 덧셈을 수행하는 가산기를 만들어보겠습니다.

이진수

우리가 사용하는 십진법은 한 자릿수가 가질 수 있는 값이 10가지(0~9)입니다. 이진법은 이와 유사하게, 한 자릿수가 가질 수 있는 값이 2가지(0, 1)밖에 없는 수 체계입니다. 그리고 각 자릿수들을 일반적으로 비트(bit)라고 부릅니다.

12 = 1100_{(2)} \\ 12 = 1 \times 10^1 + 2 \times 10^0 \\ 1100_{(2)} = 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0

12는 2진법으로 표현하면 1100과 같습니다. 십진법 숫자를 자세히 뜯어보면, 12라는 표현은 각 자릿수가 $10^k$ 의 값을 갖는다는 것을 알 수 있습니다. 이진법도 이와 마찬가지로 각 자릿수가 $2^k$ 의 값을 갖습니다. 위 식을 보면 이해가 편할거에요.

십진법 to 이진법

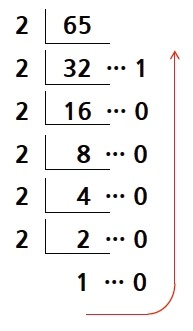
우리가 사용하는 십진법 수를 이진법으로 바꾸는 방법은 간단합니다. 각 자릿수가 2로 나눈 나머지라는 점을 이용하면 됩니다. 원래 수를 더이상 2로 나눌 수 없을 때 까지 계속 나눠줍니다. 그럼 k번 째 비트는 원래 수를 2로 k번 나눴다는 뜻이 되므로, 위에 적은 이진수 표기와 맞아떨어지게 됩니다. 가장 아래의 몫부터 역순으로 나머지들을 읽어주면, 우리가 원하는 이진법 표현을 얻을 수 있습니다.

이진법 to 십진법

이진법에서 십진법으로 바꾸는건 더 간단합니다. 각 비트가 $2^k$ 의 크기를 가지고 있으므로, 각 자릿수에 이것을 곱해주면 됩니다. 각 비트의 값이 $b_i$ 일 때 십진수의 변환 결과는 다음과 같습니다.

dec = \sum_{i=1}^nb_i\ 2^k \\ 65 = 1 \times 2^6 + 0 \times 2^5 +0 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0

논리 게이트로 adder 만들기

십진수끼리 덧셈을 할 수 있듯이, 이진수끼리 또한 덧셈을 할 수 있습니다. 또한 각 비트의 값이 0 또는 1이라는 점에서, 우리가 오늘 만든 논리게이트로 덧셈을 구현할 수 있습니다.

이진수 덧셈

초등학교 때 덧셈을 배웠던 기억을 되돌아보죠. 각 자릿수의 합을 더해서 10이 넘어가면, 받아 올림이라는 것을 했습니다. 십의 자릿수는 다음 자리로 넘기고, 일의 자리만 더한 결과로 취했습니다. 이진법에서도 마찬가지입니다. 다만, 각 자릿수는 2이상의 수를 담지 못하기 때문에, 더한 결과가 2 이상이 되면 받아 올리는 것입니다. 위 식은 $10111_{(2)}$ 와 $01101_{(2)}$ 를 더하는 과정입니다.

반가산기

비트 하나에 대해서만 생각해봅시다. 각 비트끼리의 덧셈은 두 가지의 결과를 출력합니다. 바로 더한 결과(S)와 받아 올림 여부(carry_out)입니다.

x1	x2	S	cout
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

이렇게 작동하는 가산기를 반가산기(Half Adder)라고 부릅니다. '반'이 들어간 이유는, 이전 비트에서 넘어온 받아 올림을 고려하지 않았기 때문이죠. 논리 게이트로 표현하면 다음과 같습니다.

S = XOR(x1, x2)
cout = AND(x1, x2)

구현도 간단하게 할 수 있습니다.

def half_adder(x1, x2):
    s = XOR(x1, x2)
    cout = AND(x1, x2)
    return (s, cout)

전가산기

전가산기는 여전히 비트 하나에 대해서만 계산하지만, 이전 비트에서 받아 올려진 결과 역시 고려합니다. 즉, 입력이 3개인 것입니다.

x1	x2	cin	S	cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

전가산기 역시 회로도와 진리표를 참고하여 논리게이트로 구현할 수 있습니다. (숙제)

Reference

박정훈

배우는 중입니다

이전 포스트