다음 코드로 텐서플로의 데이터를 불러온다.
from tensorflow import keras
(train_input, train_target), (test_input, test_target) =\
keras.datasets.fashion_mnist.load_data()데이터의 크기를 확인한다.
print(train_input.shape, train_target.shape)
#출력값: (60000, 28, 28) (60000,)print(test_input.shape, test_target.shape)
#출력값: (10000, 28, 28) (10000,)위의 train 데이터는 2828의 픽셀로 되어있는 이미지가 총 6만개가 있고, test 데이터는 2828 픽셀로 되어있는 이미지가 총 10000개가 있다는 뜻이다.
다음은 10개의 데이터만 이미지로 출력하는 코드이다.
import matplotlib.pyplot as plt
fig, axs = plt.subplots(1, 10, figsize=(10, 10))
for i in range(10):
axs[i].imshow(train_input[i], cmap='gray_r')
axs[i].axis('off')
plt.show()출력결과

다음은 target에 대한 데이터이다.
print(train_target[:10])
#출력값: [9 0 0 3 0 2 7 2 5 5]MNIST의 타깃은 0~9로 이루어진 레이블로 구성되어 있다. 각 숫자는 다음을 의미한다.

Tensorflow는 구글이 오픈소스로 공개한 딥러닝 라이브러리이다. 텐서플로에는 저수준 API와 고수준 API가 있다. 바로 Keras가 텐서플로의 고수준 API이다.
딥러닝 라이브러리가 다른 머신러닝 라이브러리와 다른 점 중 하나는 그래픽 처리 장치인 GPU를 사용하여 인공 신경망(ANN)을 학습한다는 것이다. GPU는 벡터와 행렬 연산에 매우 최적화되어 있기 때문에 곱셈과 덧셈이 많이 수행되는 인공 신경망에 큰 도움이 된다.
하지만 케라스 라이브러리는 직접 GPU 연산을 수행하지 않습니다. 대신 GPU 연산을 수행하는 다른 라이브러리를 백엔드로 사용한다. 예를 들면 텐서플로가 케라스의 백엔드 중 하나이다.
다른 머신러닝 모델에서는 교차 검증을 사용하여 모델을 평가했지만, 인공 신경망에서는 교차 검증을 잘 사용하지 않고, 검증 세트를 별도로 덜어내어 사용한다.
그 이유는 다음과 같다.
1. 딥러닝 분야의 데이터셋은 충분히 크기 때문에 검증 점수가 안정적이다.
2. 교차 검증을 수행하기에는 학습 시간이 너무 오래걸리기 때문이다.
따라서 검증 세트를 따로 나누기 위하여 sklearn의 train_test_split() 메서드를 사용한다
from sklearn.model_selection import train_test_split
train_scaled, val_scaled, train_target, val_target = train_test_split(train_scaled, train_target, test_size=0.2, random_state=42)우리는 현재 10개의 클래스를 가지고 있는 데이터를 사용하기 때문에, 최종적으로 나오는 뉴런의 개수(출력층)은 10개의 뉴런으로 구성된다.
다음은 케라스의 Dense 클래스를 사용하여 밀집층을 생성한다.
#밀집층 클래스인 Dense 클래스를 사용하여 밀집층을 생성.
#뉴런의 개수: 10개, 누련의 출력에 적용할 함수: softmax, 데이터 입력의 크기: 784*1
dense = keras.layers.Dense(10, activation='softmax', input_shape=(784,))첫 번째 매개변수로는 뉴런의 개수를 10개로 지정한다. 10개의 패션 아이템으로 분류하기 때문이다. 10개의 뉴런에서 출력된 값을 확률로 바꾸기 위해서는 Softmax함수를 사용한다. 만약 2개의 클래스를 분류하는 이진 분류라면 Sigmoid함수를 사용해야 한다.
마지막으로 세 번째 매개변수는 입력값의 크기이다.
위의 코드를 실행시키면 인공 신경망의 밀집층을 구현한 것이다. 이제 이 밀집층을 가진 신경망 모델을 만들어야 한다. 케라스의 Sequential 클래스를 사용한다.
#Sequential 클래스에 밀집층의 객체 dense를 전달하여 신경망 모델인 model 객체 생성.
model = keras.Sequential(dense)Sequential 클래스의 객채에 밀집층의 객체 dense를 전달했다. 여기에서 만든 model 객체가 바로 신경망 모델이다. 다음 그림에 지금까지 만든 신경망을 나타냈다. 마지막에 소프트맥스 함수를 적용한 것을 주목해라.
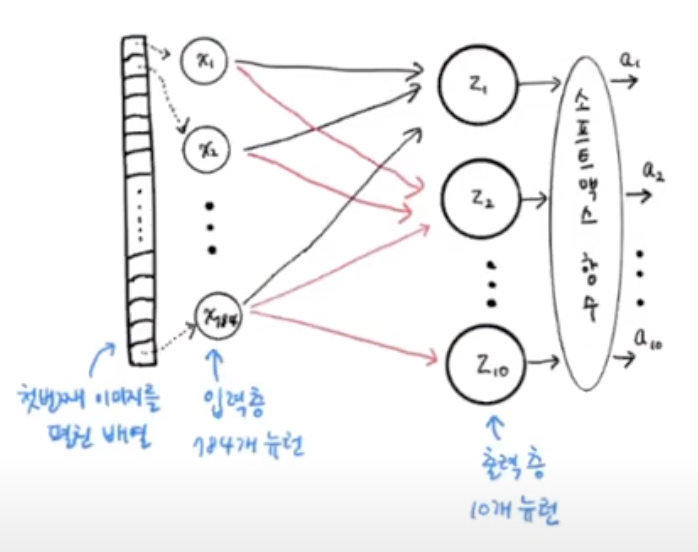
소프트맥스와 같이 뉴런의 선형 방정식 계산 결과에 적용되는 함수를 활성화 함수라 부른다.
지금까지 신경망 모델을 생성하였다. 이제 우리가 가지고 있는 학습용 데이터로 학습을 시키면 된다. 하지만 케라스 모델은 학습을 하기 전, 설정 단계가 필요하다. 이런 설정을 model 객체의 compile() 메서드에서 수행한다. 꼭 지정해야 할 것은 손실 함수의 종류이다. 다음은 compile()메서드를 이용하여 설정하는 코드이다.
model.compile(loss='sparse_categorical_crossentropy', metrics='accuracy')- 이진 분류에서는 binary_crossentropy(이진 크로스 엔트로피 손실함수)를 사용한다.
- 다중 분류에서는 categorical_crossentropy(크로스 엔트로피 손실 함수)를 사용한다.
케라스에서는 위의 두 손실 함수를 사용한다.
케라스 모델의 다중 분류는 다음과 같이 확률을 계산한다.
출력층은 10개의 뉴런이 있고, 10개의 클래스에 대한 확률을 출력한다. 첫 번째 뉴런은 티셔츠일 확률이고, 두 번째 뉴런은 바지일 확률을 출력한다. 이진 분류와 달리 각 클래스에 대한 모든 확률이 모두 출력되기 때문에 타깃에 해당하는 확률만 남겨 놓기 위해서 나머지 확률에는 모두 0을 곱한다.
예를 들어, 첫 번째 뉴런으로 분류가 되었다면, 첫 번째 뉴런의 활성화 함수 출력인 a1에 크로스 엔트로피 손실 함수를 적용하고, 나머지 활성화 함수 출력 a2~a10까지는 전부 0으로 만든다.
이와 같이 타깃값을 1로, 나머지는 모두 0으로 만드는 것을 One-Hot Encoding이라 한다.
다중 분류에서 크로스 엔트로피 손실 함수를 사용하려면 0,1,2와 같은 정수로 되어야 한다. 이러한 정수로된 타깃값을 사용해 크로스 엔트로피 손실을 계산하는 것이 바로 sparse_categorical_crossentropy이다.
케라스는 모델이 훈련할 때마다 기본으로 에포크마다 손실 값을 출력해준다. 손실이 줄어드는 것을 보고 훈련이 잘되었다는 것을 알 수 있지만, 정확도와 함께 출력이 된다면 더욱 더 좋을 것이다.
이를 위해 metrics 파라미터에 정확도 지표를 의미하는 accuracy를 지정한다.
이제 모델을 학습시켜야 한다. 다음은 케라스 모델을 학습시키는 코드이다.
#model 학습, epoch는 5로 설정.
model.fit(train_scaled, train_target, epochs=5)
#출력
Epoch 1/5
1500/1500 [==============================] - 1s 529us/step - loss: 0.4792 - accuracy: 0.8395
Epoch 2/5
1500/1500 [==============================] - 1s 524us/step - loss: 0.4570 - accuracy: 0.8481
Epoch 3/5
1500/1500 [==============================] - 1s 528us/step - loss: 0.4444 - accuracy: 0.8515
Epoch 4/5
1500/1500 [==============================] - 1s 525us/step - loss: 0.4372 - accuracy: 0.8557
Epoch 5/5
1500/1500 [==============================] - 1s 527us/step - loss: 0.4316 - accuracy: 0.8576이제 앞에서 분리한 검증 세트에서 모델의 성능을 확인해보겠다. 다음은 케라스 모델의 성능을 평가하는 코드이다.
#학습된 model의 검증.
model.evaluate(val_scaled, val_target)
#출력
375/375 [==============================] - 0s 468us/step - loss: 0.4468 - accuracy: 0.8524
[0.4468023180961609, 0.8524166941642761]