SCINet(2021)_논문 리뷰

환공지능·2022년 4월 27일

Deep Learning Time Series

[Paper Research]

목록 보기

2/4

Time Series is a Special Sequence: Forecasting with Sample Convolution and Interaction(Liu et al.; 2020, AAAI)

Univariate Time Series Forecasting에서 SOTA 모델인 SCINet에 대한 리뷰입니다.

아직 학부생이기에 부족할 수 있지만 최대한 논문의 모든 내용을 세세하게 읽고 리뷰하고자 하였습니다. 감사합니다 :)

Paper : https://arxiv.org/pdf/2106.09305.pdf

Github : https://github.com/cure-lab/SCINet

My Implementation : (추후 게시 예정)

Abstract

기존에 시계열 데이터 예측 문제에 대해 RNN, Transformer, TCN 등 다양한 딥러닝 방법론이 제안되었습니다. 그러나 이러한 모델들은 시계열 데이터의 가장 중요한 특징인 Trend, Seasonality, Irregular Component로 분해될 수 있다는 점을 간과하였습니다.

특히 Trend와 Seasonality를 활용하는 것은 예측 문제에 대한 합리적인 해결 방안이 될 것이며, 이에 영감을 받아 본 연구에서는 Sample Convolution과 Temporal Interaction을 사용한 새로운 DNN 모델을 제안하고자 합니다. SCINet(Sample Convolution and Interaction Networks)는 Downsample-Convolve-Interact 구조를 사용하여 예측 성능을 올리는 구조로 다양한 시계열 예측 문제의 벤치마크에서 Outperform함을 확인할 수 있었습니다.

1. Introduction

시계열 예측 문제(Time Series Forecasting)를 해결하기 위한 방법들이 지속적으로 연구되었습니다. 전통적인 통계 기반 모델들은 AR 부터 ARIMA, Prophet을 거쳐 발전해왔으며, 신경망 기반의 모델들도 RNN이 강세였던 시기를 지나, TCN(Temporal Concolutional Networks)나 Attention 기반의 모델들이 등장하였습니다.

💡 신경망 기반 모델의 발전과정은 아래와 같은 순서로 이루어졌습니다.
1) RNN
2) LSTM & GRU
3) Transformer
4) Transformer Based Models (Informer, Autoformer, TFT)
5) TCN
6) GNN ...

시계열 예측 문제는 일반적으로 다변량 및 단변량 문제를 구분하며, 단변량이라는 것은 변수 하나를 설정하며 미래 시점의 변수를 예측하는 것이고, 다변량이라는 것은 다수의 변수를 활용하는 것을 의미합니다. 예를 들면 주가를 예측한다고 가정했을 때, 주가 그 자체로 예측하는 것은 단변량 문제이나, 해당 기업의 경제 지표, 거시 경제 지표, 뉴스 등의 데이터를 활용하는 것은 다변량 문제가 되는 것입니다.

그러나 기존의 시계열 분석 기법들에서는 Trend나 Seasonality는 잘 고려하지만 Irregular Component를 잘 고려하지 못한 바, SCINet을 이를 해결하고자 제안하는 바입니다.

📌 SCINet의 주요 골자는 다음과 같습니다.

시계열 데이터의 특징에 기초하여 다양한 시계열 해상도로부터 반복적으로 추출되고 교환하는 계층적인 TSF Framework를 제안하고자 합니다.
계층적인 구조를 위해 SCINet의 구성요소이자 기본 단위인 SCI Block을 제안하며, SCI Block은 입력 시계열이나 데이터를 다운 샘플링하고, 그 특징들을 추출하는 역할을 수행합니다.

SCINet을 검증하기 위하여 본 연구에서는 ETT Dataset을 사용하여 실험하였으며, Informer나 Informer를 개량한 Yformer보다 더 좋은 성능을 보임을 확인할 수 있었습니다.

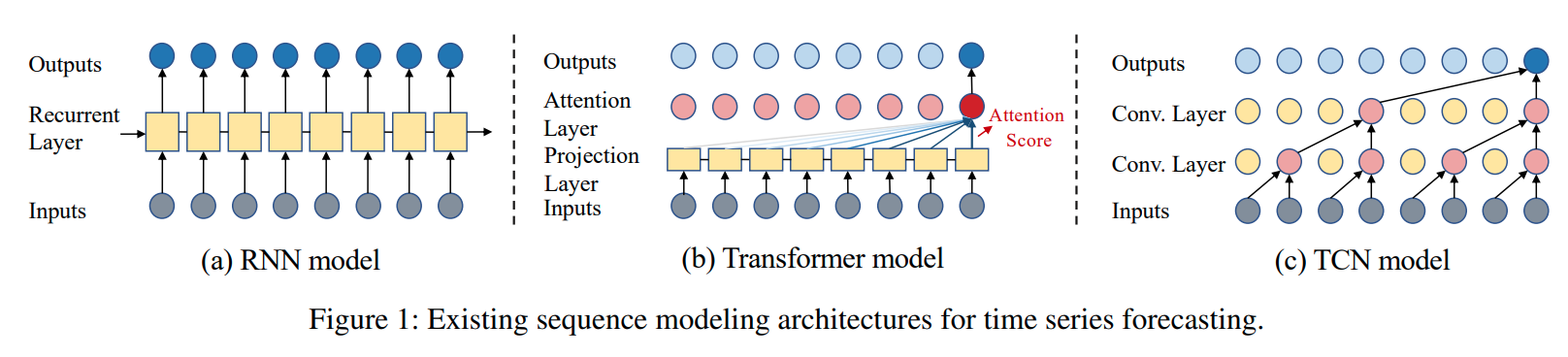
RNN 기반의 TSF 방법론은 그림 (a)와 같이 과거의 정보를 압축하여 내부 메모리에 저장하고, 각각의 time step에 따라 새로운 input이 들어오면 메모리를 업데이트하는 방식입니다. 그러나 이와 같은 방식은 error accumulation 문제와 gradient vanishing/exploding 문제로 인하여 제약이 큽니다.

Transformer 기반 모델은 Self-attention mechanism을 사용하여 거의 모든 데이터에서 RNN 기반 모델을 대체하였습니다. TFT, Informer, Yformer와 같이 Transformer 기반의 모델이 다수 제안되었으며 긴 시퀀스에 대한 예측 문제에서 꽤 효과를 보이기도 하였습니다. 그러나 모델의 크기가 크고 계산 복잡도가 크다는 Overhead 문제가 존재하며 이 문제를 해결하기 위해 Transformer 기반 모델들에 대한 다양한 연구가 진행 중입니다.

CNN 기반의 모델은 시계열 데이터에 존재하는 Local correlation을 잘 반영하기 때문에 TSF 문제에서 가장 많은 선택을 받았으며 Convolutional filter는 Spatial-Temporal TSF 문제를 해결하는 분야에서 광범위하게 사용되고 있습니다.

본 연구에서 제안하는 SCINet은 TCN을 기반으로 하고 있으나 기존의 모델과 비교하여 Dilated Causal Convolution 측면에서 차이가 있기에 아래에서는 본 연구의 인사이트와 새로운 점을 강조하고자 합니다.

2.2 Rethinking Dilated Causal Convolution

Causal Convolutions

시퀀스 모델링을 입력 시퀀스 $x_0, ..., x_T$ 에 대하여 출력 시퀀스 $y_0, ..., y_T$ 를 예측하는 문제로 정의한다면 입력을 출력으로 매핑하는 최적의 함수 $f$ 를 찾는 것이라고 정의할 수 있습니다.

\hat y_0, ... \hat y_T = f(x_0, ..., x_T)

여기에서 중요한 점은 시계열 데이터의 특성 상 $t$ 시점의 출력은 미래에 의존하지 않고 현재와 과거에만 의존한다는 causality를 만족해야 한다는 점입니다. 이 때문에 TCN은 1차원 Convolution을 사용하여 'kernel 크기 - 1' 만큼의 zero-padding을 전체 시퀀스의 길이를 유지하기 위해 양쪽에 붙이게 되며, 시퀀스 길이 이후 Convolution한 결과물을 잘라내어 미래 시점의 정보가 현재 시점의 출력으로 흐르지 않도록 방지합니다. 이를 Causal Convolution이라고 합니다.

Dilated Convolutions

일반적인 1차원 Convolution으로 멀리 떨어진 time step의 정보를 파악하기 위해서는 매우 많은 Layer와 Filter가 필요합니다. 이를 극복하기 위해서 TCN에서는 WaveNet 모델에서 사용하는 Dilated Convolution을 이용합니다.

그림 (c)는 전형적인 TCN 구조를 보여줍니다. Dilation factor와 Causal convolutional layers를 통해 많은 양의 정보를 저장할 수 있는 형태이며, TCN 기반의 구조는 모든 형태의 시계열 예측 문제에 광범위하게 사용되고 있습니다.

Downsample-convolve-interact Architecture

기존의 Dilated Convolution은 적은 수의 Convolutional layer를 사용하여 더 많은 정보를 수용할 수 있었으나, 단 하나의 Convolutional filter가 모든 층에 걸쳐 공유되기 때문에 이전 Layer의 Temporal Dynamics를 추출하는데 제약이 크다는 단점이 있었습니다. 이에 SCINet에서는 Downsample-Convolve-Interact 구조를 사용하여 시계열 데이터가 가지는 특성을 온전히 사용하여 예측 성능을 높이고자 합니다.

3. SCINet : Sample Convolution and Interaction Networks

긴 시계열 $X*$ 와 고정된 $T$ 길이의 윈도우, 그리고 Time step $t$ 가 주어진 경우, 과거 $T$ 로부터 현재까지의 입력 시계열 $X$ 에 기반하여 예측한 시계열 $\hat X$ 는 다음과 같이 표현할 수 있습니다.

\hat X_{t+1:t+\tau} = x_{t+1}, ... , x_{t+\tau}

X_{t-T+1:t} = x_{t-T+1}, ... , x_{t}

이 때, $\tau$ 는 예측할 시계열의 길이이고, 각 시점 $t$ 의 값인 $x_t$ 는 $d$ 차원의 실수입니다.

3.1 SCI-Block

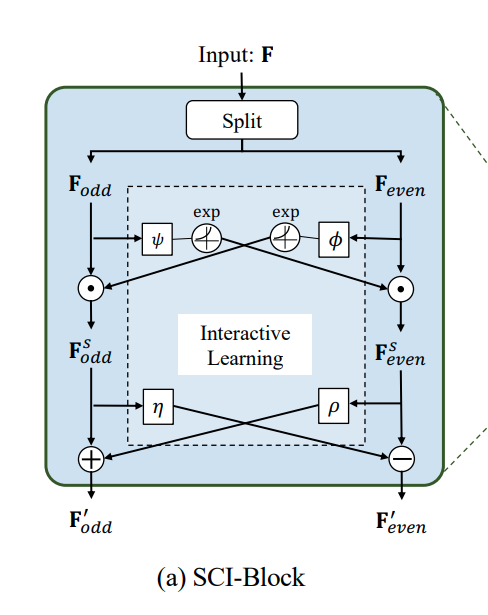
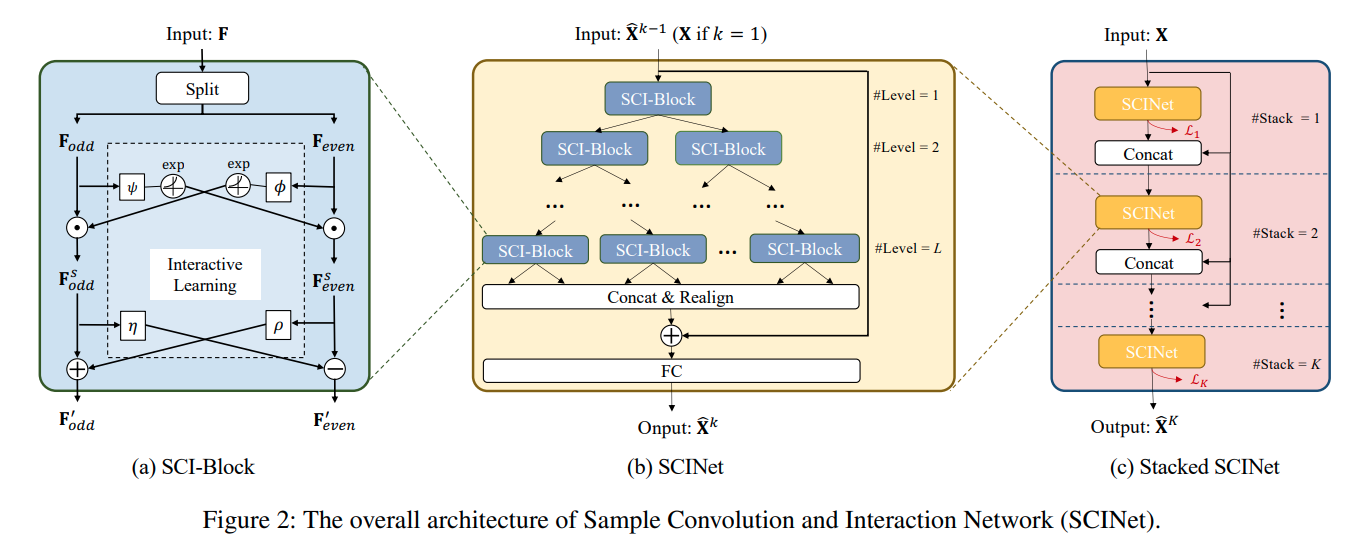
한편, SCINet의 기본 유닛인 SCI-Block은 위와 같은 구조를 갖습니다. 입력 시계열 또는 Feature들을 의미하는 $F$ 는 $F_{odd}$ 와 $F_{even}$ 으로 나뉜 후 Interactive Learning을 활용한 특징 추출 과정을 거치게 됩니다.

그림의 $\circ$ 는 element-wise product라고도 불리는 Hadamard product이며, $\psi, \phi, \eta, \rho$ 는 서로 다른 convolutional kernel을 의미합니다.

나뉜 $F_{odd}$ 와 $F_{even}$ 은 각기 다른 $\psi, \phi$ kernel과 exponential 함수를 순차적으로 통과하며, 전달받는 값과 element-wise product를 계산하여 $F_{odd}^s$ 라는 feature로 변환됩니다. 반대쪽의 경우 각기 다른 $\eta, \rho$ kernel과 +-연산자를 활용하여 SCI-Block의 Feature인 $F_{odd}', F_{even}'$ 을 출력하며 위의 과정을 식으로 정리하면 아래와 같습니다.

F_{odd}^{s} = F_{odd} \odot \exp ( \phi ( F_{even} ) )

F_{even}^{s} = F_{even} \odot \exp ( \psi ( F_{odd} ) )

F_{odd}' = F_{odd}^{s} + \rho ( F_{even}^{s} )

F_{even}' = F_{even}^{s} - \rho ( F_{odd}^{s} )

이와 같은 과정을 통해 시계열 예측을 위한 Long-Term, Short-Term Dependency를 반영할 수 있습니다.

3.2 SCINet

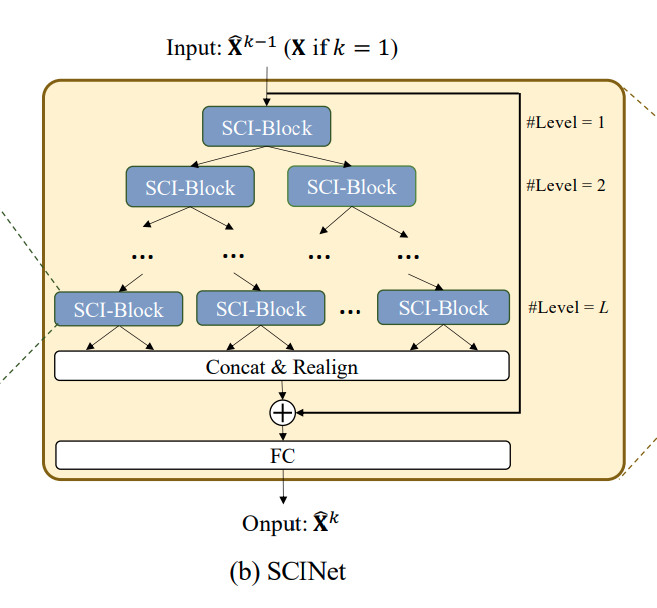
나뉜 $F_{odd}'$ 와 $F_{even}'$ 은 입력 시계열 길이 $T$ 의 절반이 됩니다. 따라서 SCI-Block을 활용하여 Binary Tree의 구조로 만든 것이 SCINet이며 트리의 깊이 $k$ 가 깊어질수록 추출되는 시계열의 길이는 $\frac{T}{2^k}$ 를 만족하게 됩니다.

$L$ 레벨까지 추출된 Feature들은 길이가 $T$ 인 새로운 Feature들의 시계열 데이터로 병합할 수 있지만 순서가 Binary Tree에 따라 섞여 있는 바, 추출된 Feature들을 병합하고 정렬한 후 입력 시계열의 Residual Connection을 더해줍니다. 마지막으로 FC Layer는 시계열의 길이를 $T$ 에서 $\tau$ 로 바꾸어주는 역할을 수행합니다.

3.3 Stacked SCINet

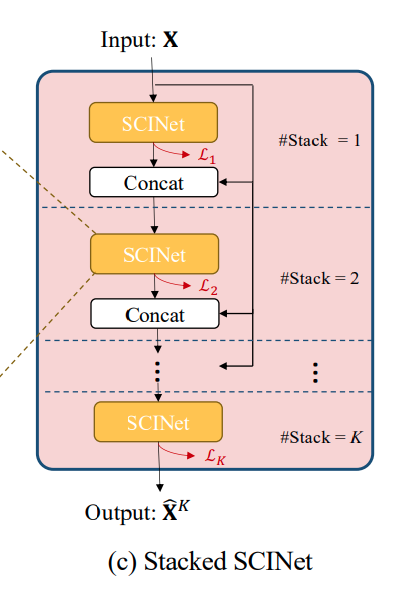
마지막으로 SCINet을 $K$ 개 만큼 Stack 합니다. 특별히 K개의 SCInet을 비슷한 관점으로 학습하기 위해 Loss Function을 다음과 같이 구성합니다.

\mathcal{L}_k = \frac{1}{\tau} \sum_{i=0}^{\tau} \parallel \hat{x}_i^k-x_i \parallel

\mathcal{L} = \sum_{k=1}^{K} \mathcal{L}_k

🔎 SCINet이 제안한 구조의 특징들은 아래와 같은 특징이 있습니다.
(1) 서로 다른 convolutional kernel을 가집니다.
(2) Inter-learning이 구현되어 있습니다.
(3) Residual connection을 가집니다.
(4) Linear Enhancement가 있습니다.

본 연구에서는 위에서 제안한 4가지 요소가 유효함을 증명하기 위해 4가지 요소를 모두 적용하였을 때와 각기 다른 한가지 요소들을 제외하였을 때의 성능 차이를 비교하는 방식으로 실험을 진행합니다.

4. Experiments Results

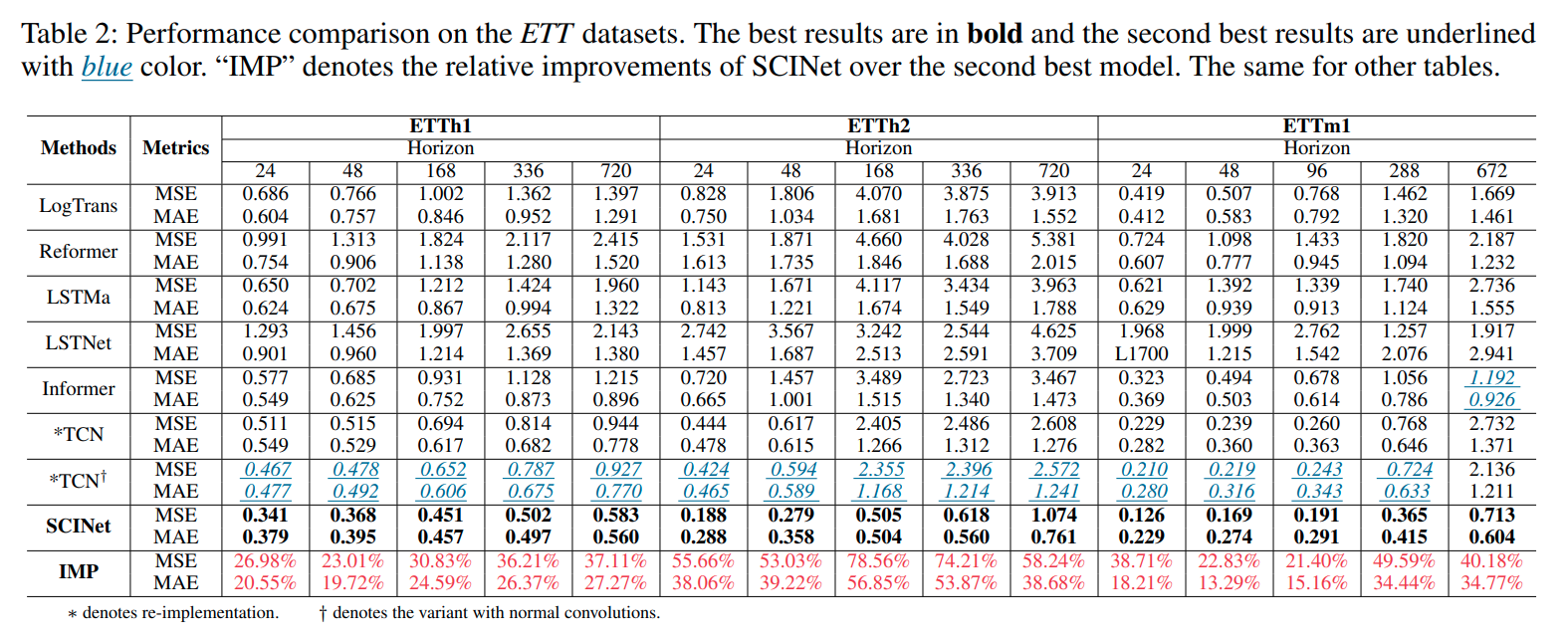
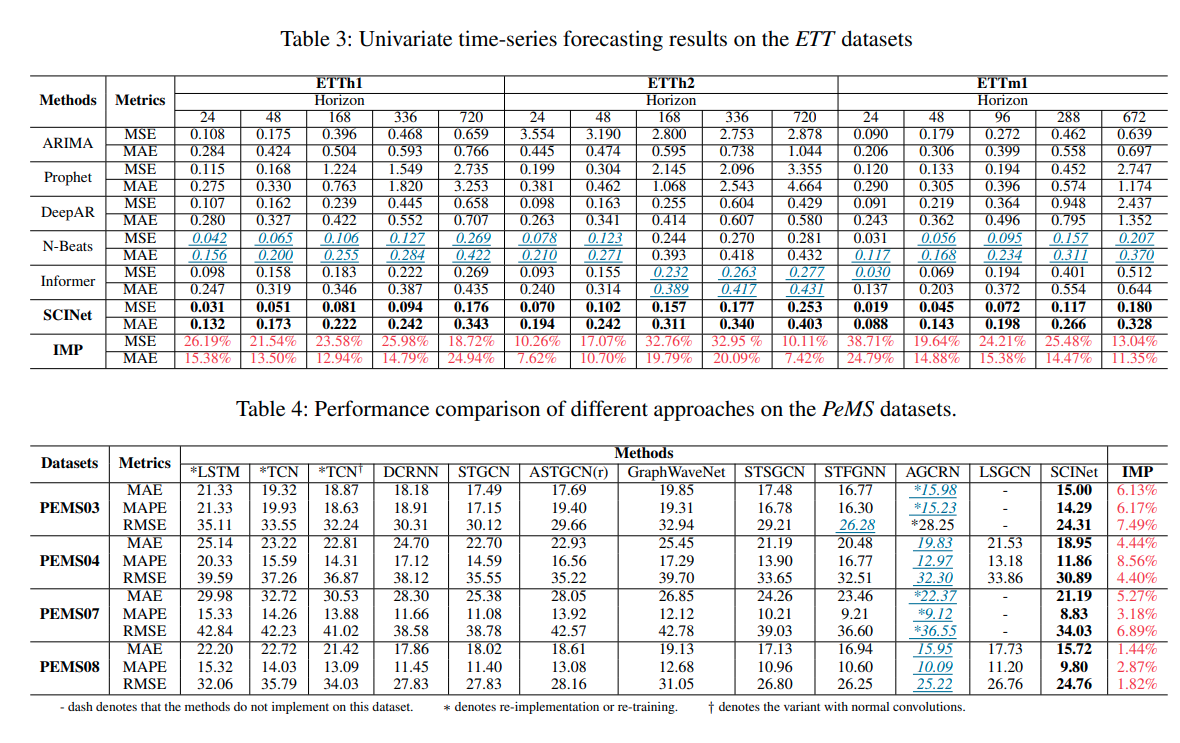
본 연구에서는 ETT Dataset을 활용하여 다양한 길이의 시계열 예측을 시도하였고, SCINet이 ETTh2(720)을 제외한 모든 데이터에서 최고의 성능을 가짐을 확인할 수 있었습니다.

최근에 제안된 LogTransformer, Reformer, Informer는 물론 TCN과도 성능 비교를 하였으며, 확연한 성능 개선을 확인할 수 있었습니다.

5. Conclusion

현실 세계의 다양한 시계열 데이터는 Regular Time Series가 아니라 Irregular Time Series인 바, SCINet은 노이즈가 많은 현실 세계의 데이터에 대해 Downsampling과 Interactive Learning을 통해 강건한 성능을 가질 수 있을 것입니다.

Downsampling Mechanism과 관련하여 불규칙한 Interval의 Sampling이 불가능하다는 한계가 있지만 거의 모든 시계열 벤치마크에서 SOTA를 달성한 만큼 SCINet의 잠재력이 무궁무진하다고 볼 수 있습니다.

.
.
.

References

환공지능

데이터사이언티스트 대학원생

이전 포스트

Temporal Fusion Transformer(2020)_논문 리뷰

다음 포스트

SCINet(2021)_논문 리뷰

[Paper Research]

Time Series is a Special Sequence: Forecasting with Sample Convolution and Interaction(Liu et al.; 2020, AAAI)

Abstract

1. Introduction