
💡오늘 배울 내용
신경망 학습에서 꼭 필요한 편미분 기초 내용을 살펴봅시다.
🔎미분
편미분을 배우기에 앞서, 미분법을 복습하고 "미분한다"의 의미를 확실히 이해해봅시다.
🔔평균 변화율
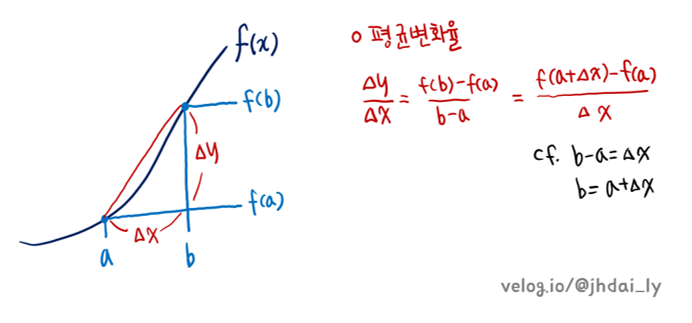
평균 변화율은 주어진 구간에서 y값이 평균적으로 변화한 양을 의미합니다.
기하적으로는 그래프에서 구간의 양 끝점을 잇는 직선의 기울기를 뜻하고, y의 변화량을 x의 변화량으로 나누어 구할 수 있습니다.
🔔순간 변화율
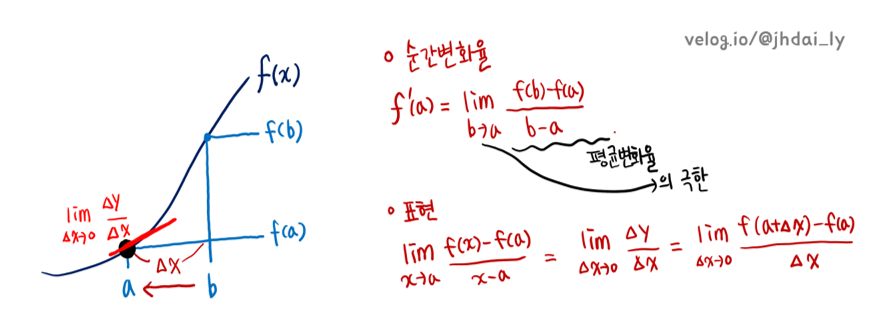
순간변화율은 구간에서의 평균적인 변화율인 평균 변화율과 달리, 한 점에서의 순간적인 개념입니다.
즉, 어느 한 점의 접선의 기울기를 뜻한다고 말할 수 있습니다.
순간 변화율은 평균 변화율의 극한을 통해 정의할 수 있습니다. 예를 들어, b가 a로 한없이 가까워질때 a에서의 접선의 기울기를 f'(a)라고 표현하고 이 값을 순간적인 변화율(=미분 계수 =접선의 기울기)라고 부르는 것입니다.
🔔"미분한다"
"미분한다"는 말은 도함수를 구한다는 것으로, 도함수는 입력 x에 대해 함수 f가 얼마나 민감하게 변화하는지(순간변화율)을 알려주는 함수입니다.
🔎편미분
신경망을 학습할때, 파라미터 하나의 변화가 전체에 미치는 영향을 구하기 위해 편미분 개념을 사용합니다. 보통 다변수 함수에서 정의됩니다. 특정 변수를 기준으로 하고 나머지 변수들을 상수취급하므로 변수가 하나 이상이여야 하기 때문입니다.
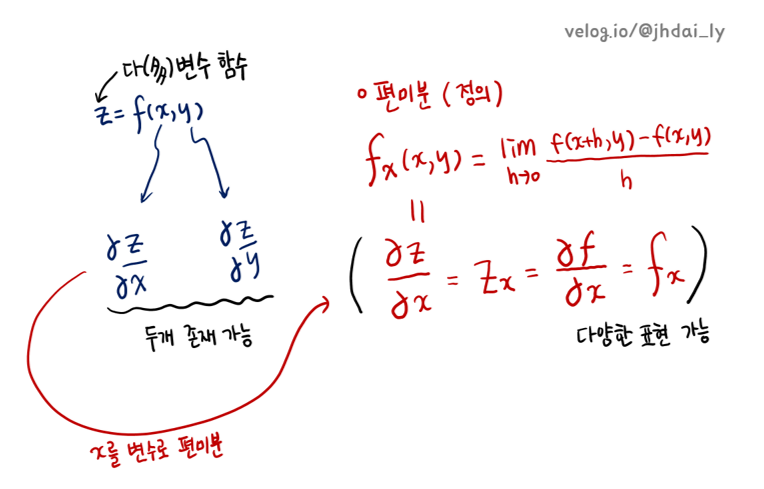
편미분은 다변수 함수에서 하나의 변수를 기준으로 미분하는 것입니다. 예를 들어, 함숫값 z에 x가 주는 영향을 계산하고 싶을때 x만 변수로 두고 미분을 시도할 수 있습니다.
🔎클레로의 정리
어떤 함수를 x에 관해 편미분 한 후, y에 관해 편미분을 한 함수와 y에 관해 편미분 한 후, x에 관해 편미분을 한 함수는 항상 같다고 할 수 있을까요?
클레로의 정리에 의하면, '어떤 조건'을 만족할때 편미분을 하는 순서는 중요치 않다고 합니다.

우선 3차원 공간상에 정의되는 이변수 함수인만큼 점 (a, b)의 근방을 주목해야합니다. (a, b)를 포함하는 근방에서 fx, fy, fxy, fyx가 존재하고 동시에 연속하면 fxy(a, b)는 fyx(a, b)와 같은 값을 갖게 됩니다.
클레로의 정리를 사용하면 여러번 편미분 하는 상황에서 간단하게 계산할 수 있습니다. 예를 들어 특정 변수를 먼저 미분하면 상수(0)이 되어버리는 상황에서 그 변수를 우선적으로 미분하면 됩니다.
🔎편미분의 기하적 의미
y = f(x)에서 x = a 에서의 미분계수 f'(a)는 (a, f(a)) 에서 접하는 접선의 기울기라는 기하적 의미를 갖습니다.
이변수 함수 z = f(x, y)의 기하적 의미를 설명하기 위해선 3차원 공간상에 그려지는 곡면을 떠올려야 하는데요, 면 위의 점 (x, y) 위에 떠오르는 공간상의 점 z를 기준으로 하기 때문입니다.
공간상의 점 z를 기준으로, 어떤 방향으로든지 미분계수를 구할 수 있지만 편미분을 한다는 것은 축 방향으로만 생각하겠다는 말입니다. 즉, 이변수 함수에서는 x와 y축 방향으로만 방향미분계수를 구하겠다는 의미입니다.
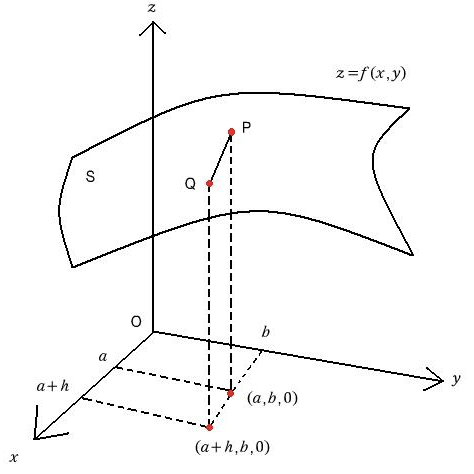
해당 그림은, x를 변수로 놓고 편미분을 시도하는 과정을 나타내고 있습니다.
y위의 점 b가 고정되었을때, x가 a에서 a+h로 변화함에 따라 곡면 PQ의 기울기를 정의할 수 있습니다. 이때 x의 변화량이 점점 작아지면(h가 0에 점점 가까워지면) P와 Q를 잇는 선분은 점 P에서의 접선에 가까워집니다.
이때의 접선의 기울기, 즉 xz 평면에 평행한 x축 방향으로의 접선의 기울기를 x를 변수로 두고 편미분했을때의 기하적 의미로 설명할 수 있습니다.


안녕하세요:) 지나가다 댓글 남겨요!! 이 글 보니까 새내기 때 미적분 공부했던 공부가 새록새록 나면서 두근거렸네요. 그림그려가면서 설명해주시니 오랜만에 보는 내용인데도 한번에 이해됐어용 파이팅입니닷