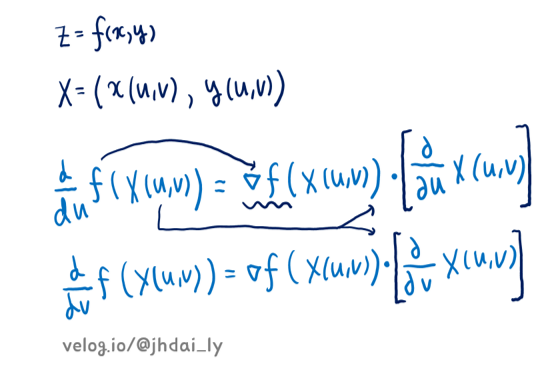💡오늘 배울 내용
합성함수로 정의된 벡터함수를 살펴보고, 이를 편미분하는 과정을 학습합니다. 이 과정에서 다변수 함수의 미분계수인 기울기벡터장(gradient)가 등장하는데, 이는 방향도함수 파트에서도 매우 중요한 용어와 개념입니다.
🔎벡터함수
다변수 함수의 합성함수를 생각해보기에 앞서, 일변수 함수의 합성함수 f(g(x))를 살펴봅시다. x가 함수 g를 통과하여 g(x)가 되고, g(x)가 또다시 함수 f의 원소가 되려면 함수 g의 치역이 f의 정의역이 되어야 합니다.
다변수 함수에서도 마찬가지로 합성함수 f(X(x, y))를 살펴보면, 합성함수 f(X(x, y))의 정의역으로 X(t) = (x(t), y(t))나 X(u, v) = (x(u, v), y(u, v)) 등의 함수가 필요하고, 이와 같은 함수가 결국 벡터함수임을 알 수 있습니다.
벡터함수는 실수값을 벡터에 대응시키는 함수로, z = f(x, y)를 어떤 함수와 합성시키는 과정에서 자연스럽게 벡터 함수가 구성됩니다.
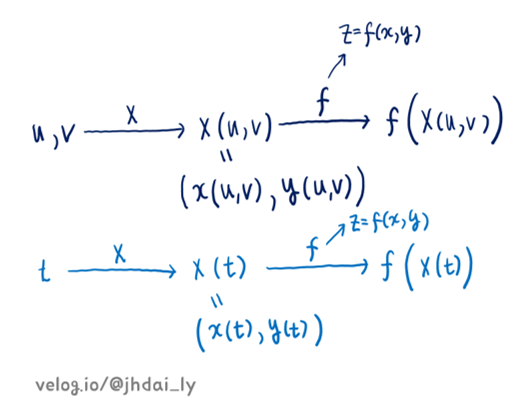
🔎벡터함수의 미분
함성함수 f(X)에서 X가 X(u, v)일 수도, X(t)일 수도 있다고 했습니다. 합성함수 f(X)를 미분, 혹은 편미분 하기에 앞서 속함수 X를 어떻게 미분할 수 있을지 살펴봅시다.
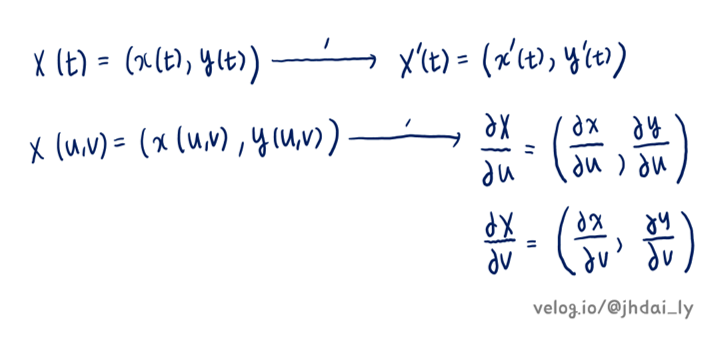
속함수가 X(t)인 경우 x(t)와 y(t)는 같은 변수로 된 함수이므로 X'(t)도 각각에 미분을 함으로써 구할 수 있습니다. X(u, v)인 경우는 이변수 함수라서 u를 기준으로, v를 기준으로 각각 편미분을 할 수 있으므로 X'(u, v)도 두가지의 경우로 나뉠 수 있습니다.
🔎기울기 벡터장(gradient)
참고로 다변수함수 z = f(x, y)의 미분계수는 아래의 벡터장으로 표현됩니다. 이를 기울기벡터장(gradient)라고 부르고, ∇f = (fx, fy)처럼 씁니다.
기울기벡터장이 어떠한 의미를 갖는지, 기하학적으로 방향도함수와 어떻게 엮일 수 있는지는 방향도함수를 다룰때 다루기로 하겠습니다. 이번 연쇄법칙 챕터에서는 합성함수 f(X)를 미분하는 과정에서 필요한 겉미분(f')을 위해서 z의 미분계수를 도입하는 것입니다.
🔎연쇄법칙(1)
연쇄법칙(1)에서는 속함수가 X(t)인 경우를 다루도록 하겠습니다.
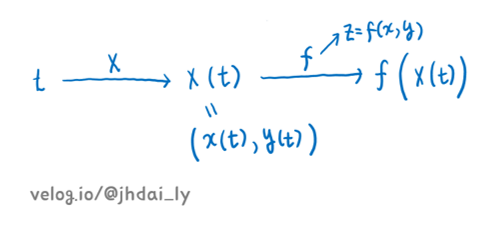
일변수 함수가 속함수인 합성함수 f(g(x))를 미분할때는 겉미분과 속미분을 곱한 결과로 미분이 진행됩니다. 즉 f(g(x))를 미분하면 f'(g(x))*g'(x)가 그 결과로써 도출됩니다.
마찬가지로 이변수 함수가 속함수인 합성함수 f(X(t)) = f(x(t), y(t))를 미분할때도 겉미분과 속미분을 곱한 결과가 미분의 결과가 됩니다.
위에서 X(t)와 f를 어떻게 미분하는지 배웠습니다. 즉, X'(t)와 ∇f를 곱한 결과가 f(X(t))의 미분 결과가 됩니다. 참고로 벡터 함수이므로, X'(t)와 ∇f를 곱하는 과정은 내적 연산으로 구해야 합니다.

🔎연쇄법칙(2)
연쇄법칙(2)는 속함수가 X(u, v)인 경우입니다.
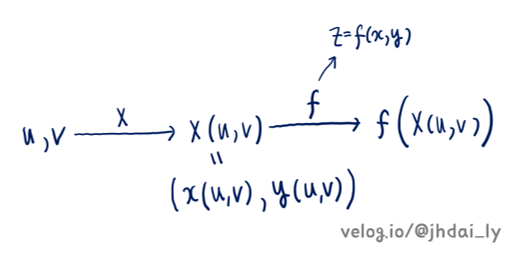
이 경우도 마찬가지로, 속미분과 겉미분을 내적 연산 한 형태로 미분이 진행된다고 할 수 있습니다. 하지만 속함수 X(u, v)를 미분하는 방법은 위에서 설명했던 것 처럼 두가지가 있을 수 있어 f(X(u, v))의 미분 결과도 두가지가 있습니다. u로 미분했을때(u를 기준으로 편미분), v로 미분했을때(v를 기준으로 편미분) 이렇게 두가지입니다.