
💡오늘 배울 내용
방향도함수의 개념과 크기를 구하는 공식, 그리고 기하학적 의미까지 배워봅시다.
또한 gradient 방향이 무엇을 의미하는지, 기울기 벡터장의 의미를 살려 이해해봅시다.
🔎방향도함수의 도입

https://velog.io/@jhdai_ly/미분적분학편미분-미분-순간-변화율-편미분의-개념-편미분의-기하학적-의미
편미분의 기하학적 의미 포스팅에서, 편미분은 공간상의 점 z를 기준으로 축 방향에서만 생각하여 미분계수를 구하는 것이라는 설명을 했었습니다.
그렇습니다. 이변수 함수 z = f(x, y)는 3차원의 공간 상에서 그래프가 그려지고, 공간상의 한 점을 기준으로 생각하면 수많은 방향에서의 기울기(방향미분계수)가 고려될 수 있는 것입니다.
방향도함수의 미분계수, 방향미분계수가 공간상의 점을 기준으로 한 기울기라고 가볍게 생각하고, 이제 어떻게 방향도함수가 정의되는지 살펴봅시다.
🔎방향도함수의 정의

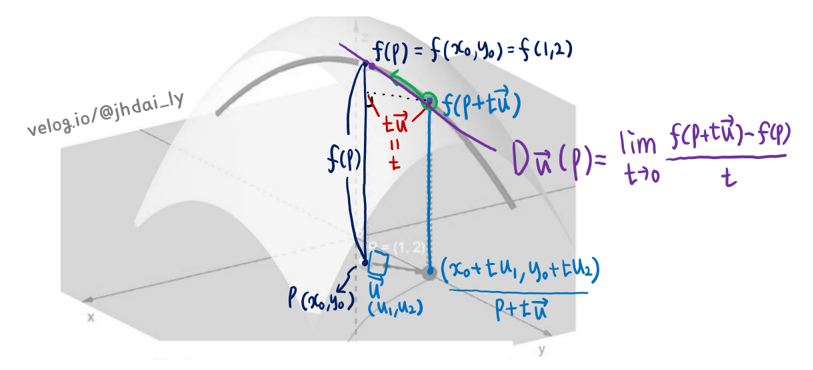
역시 방향도함수를 정의하는 과정에서 방향(u), 한 점(P), 함수(f) 세가지 정보가 필요함을 알 수 있습니다. 어떤 방향으로 기울기를 구할 것인지(방향 미분계수를 구할 것인지) 단위벡터(u)를 통해 알 수 있는 것입니다.
방향도함수의 정의식이 왜 다음과 같이 나오는지 그림을 통해 확인해 볼 것입니다. 공간상의 점에서 특정 방향을 기준으로 구한 기울기가 방향미분계수임을 미리 이해하고 그림을 살펴보면 이해하기 쉽습니다.
🔎방향도함수와 gradient
Chain Rule 포스팅에서 gradient는 다변수 함수에서의 미분계수라는 설명을 했습니다. f(x, y) 함수에서 x축과 y축으로 편미분계수를 구한 것을 ∇f = (fx, fy)처럼 벡터로 묶어 나타낸 것입니다.
이변수함수의 합성함수 미분을 진행하며 f'를 구하기 위해 gradient를 설명했지만, gradient는 사실 방향미분계수를 구하는대도 매우 중요한 역할을 합니다. gradient(∇f)와 방향을 나타내는 단위벡터(u)를 내적연산하면 그 방향으로의 방향미분계수를 구할 수 있기 때문입니다.
즉, gradient를 알면 모든 방향에서의 미분계수를 구할 수 있는 것입니다.

🔎방향미분계수의 크기

앞서서 gradient와 방향을 내적연산하여 방향 미분계수를 구할 수 있다고 배웠습니다.
추가로 설명하면, 방향도함수의 미분계수는 gradient 값과 코싸인 값을 곱하여 구할 수 있는데요. 이 경우에서 코싸인에 들어가는 세타(θ)는 단위벡터가 나타내는 방향과 gradient 방향의 사이 각도를 의미합니다.
그래서 점이 고정되어있어 ∇f(x)가 상수인 상황에서는, 방향미분계수의 크기가 cosθ의 영향을 받는 것입니다. 코싸인 함수는 최대 최소를 갖는 점의 좌표가 정해져있어, 방향미분계수의 크기 또한 최대 혹은 최소를 갖는 좌표가 정해져있습니다.
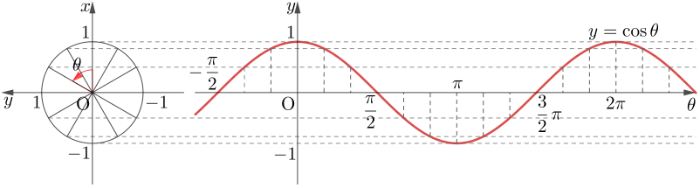
세타(θ)가 0와 2𝝿에서 코싸인 함수는 1로 최대값을 갖는데, 이는 gradient 방향과 단위벡터가 나타내는 방향이 같다는 것을 나타냅니다. 즉, 단위벡터가 나타내는 방향과 gradient 방향이 같을 때 방향 미분계수는 최대값을 갖을 수 있습니다.
🔎gradient 방향
방향 미분계수의 크기를 설명하며 gradient 방향이라는 개념이 자주 나왔습니다.
여기서 gradient 방향, 즉 기울기벡터장의 방향이 무엇인지 자세히 살펴보겠습니다.
이변수 함수를 기준으로 기울기벡터장은 ∇f = (fx, fy)처럼 쓰고 나타냅니다. 이때 이 기울기벡터장을 2차원의 그림으로 나타낼 수 있는데요, x축 성분과 y축 성분이 합쳐진 벡터를 하나의 화살표로 표현하는 것입니다.
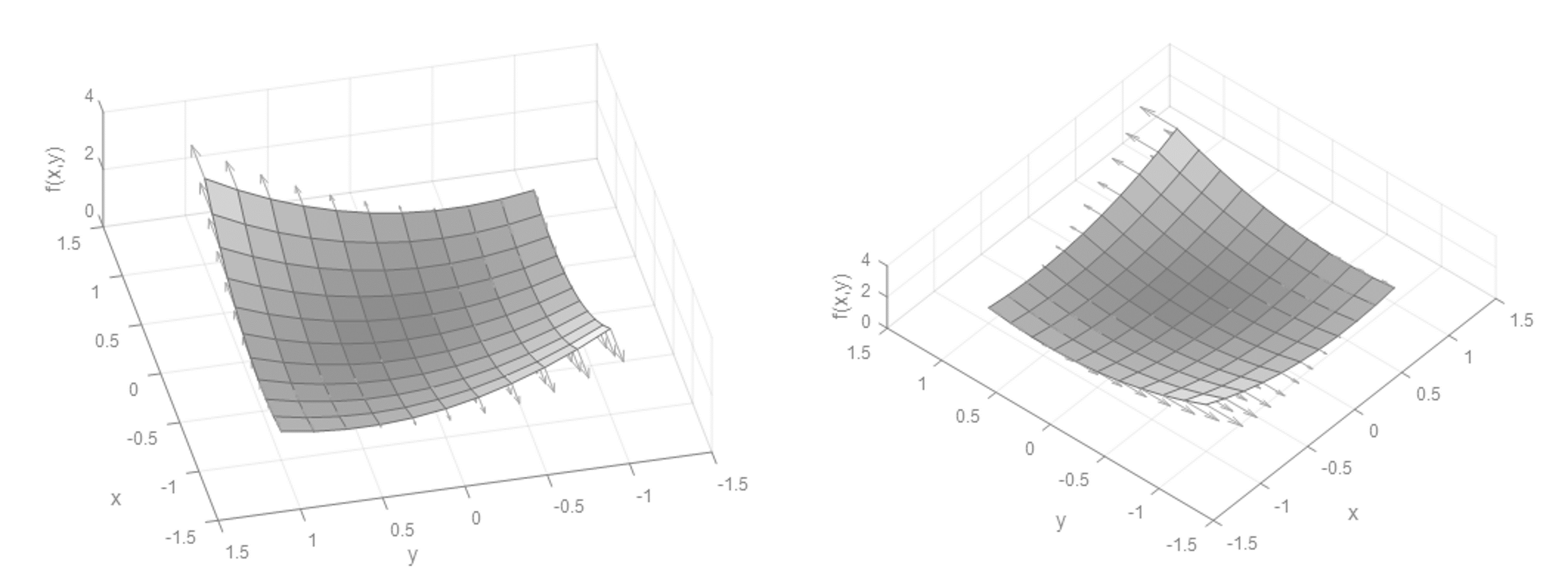
위의 그림은 f(x,y) = x^2 + xy + y^2를 그림으로 그린 후 벡터 성분을 화살표로 표현한 그림입니다. 첫번째 그림은 x축 벡터 성분만을 기준으로 하였고(각 좌표에서 x를 기준으로 구한 기울기=편미분계수), 두번째 그림은 y축 벡터 성분만을 표현하였습니다.
그렇다면 이 두 성분을 합쳐서 표현할 수 있지 않을까요?
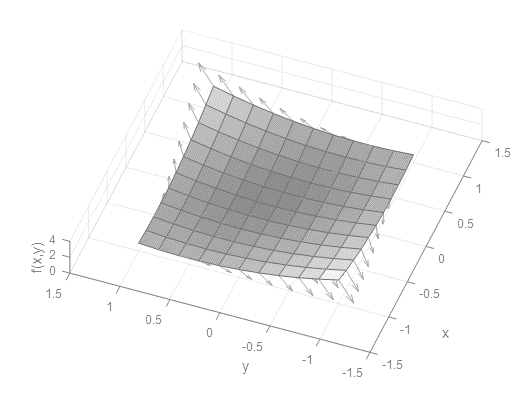
∇f를 이용하여 x축과 y축 방향 성분을 합쳐 화살표로 그려보면 다음과 같은 형태를 띄게 됩니다. 화살표가 가르키는 방향이 gradient방향으로, gradient 방향은 함수값이 증가하는 방향을 가르키고 있다고 볼 수 있습니다.
