MST(최소 신장 트리)
신장트리
- 무향(방향이 없다
- 사이클 x
--> 여기서 비용이 최소인 것이 최소 신장 트리(모두 연결 최소 비용)
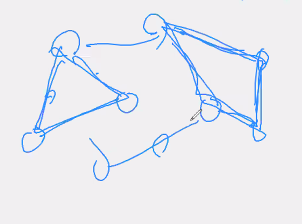
이러한 사이클이 없어야 함.
크루스칼 알고리즘
어떻게 연결해야만 사이클이 안생기고 최소로 연결할 수 있는지
간선을 따라 최소 비용인 정점을 탐색
- 서로소 집합을 이용해 사이클 여부를 확인할 수 있음
- 싼 노드랑 비싼 노드 정렬 -> 싼 노드 선택해 연결 반복(모두 연결할 때까지 V-1번/사이클 생기면 버려야 됨)
서로소 집합
공통 원소가 없는 두 집합
- union(합집합으로 만듬), find(특정 원소가 속한 집합이 무엇인지) 연산으로 조작 가능
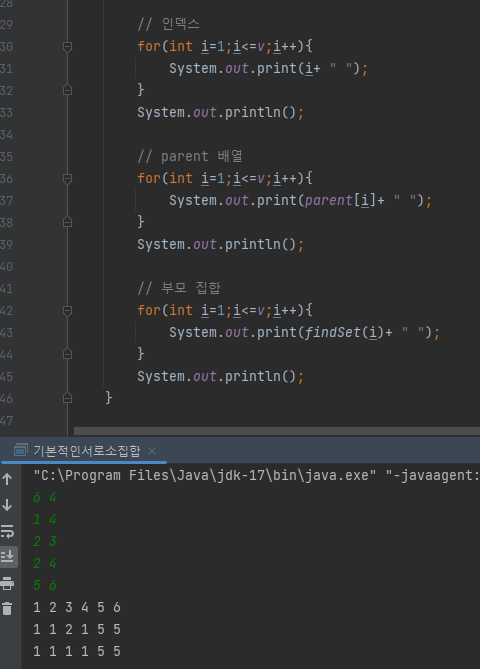
서로소 집합 findSet()에서 parent[] 배열에 관해
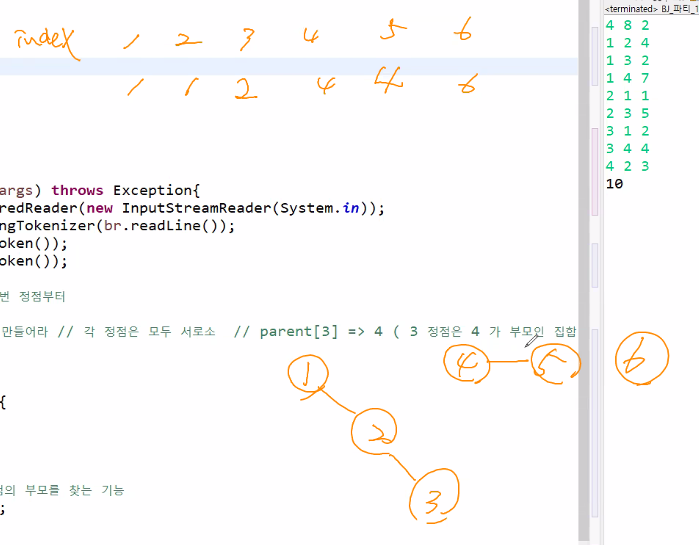
findSet(4) = 1, findSet(5) =1 처럼 같은 값을 가지면 이미 그 집합에 속해있다.
-> 이때 4와 5를 연결하면 사이클이 생김
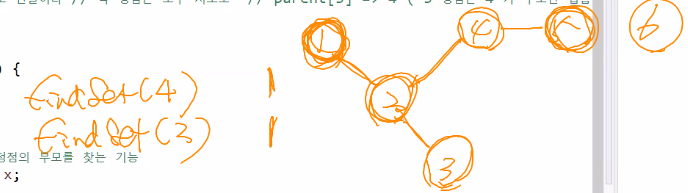
서로 다른 집합일 때 union을 해야함
프림 알고리즘
시작점 하나를 잡고 가장 가까운 노드를 찾아가 V를 만들어 가는 알고리즘
- 갈 수 있는 노드 중에 가장 비용이 적은 정점을 고름 -> 우선순위 큐 사용
(다익스트라와 비슷 - 하지만 꺼낸 다음에 cost를 만들 필요는 없다) - 노드 중심으로 탐색하여 가장 비용이 적은 정점을 선택
-> 간선이 많은 경우는 프림 알고리즘, 간선이 적은 경우는 크루스칼 알고리즘이 유리함
조별시간에 프림과 다익스트라가 어떤 점이 다른가에 대해 의문이 생겨 토론하였다.
프림 vs 다익스트라
프림
- 최소 신장 트리를 만드는 것으로
- 각 정점에서 자신과 연결된 간선의 가중치를 저장
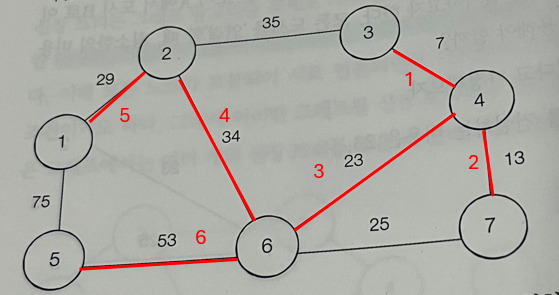
다익스트라
- 한 정점에 대한 최단 경로를 구함
- 시작 정점이 바뀔때마다 최단 경로가 바뀜
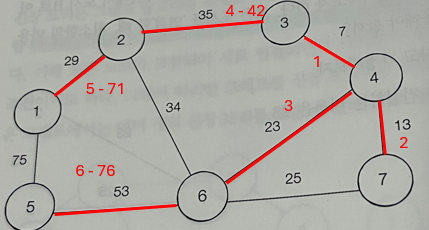
백준 도시 분할 계획
https://www.acmicpc.net/problem/1647
골드 4, MST 문제다.

문제를 처음에 이해를 못했었다.
아예 연결되어있지 않은 상태에서 마을을 2개로 분할하는 방법을 모두 따져야 하는건가 생각했다.
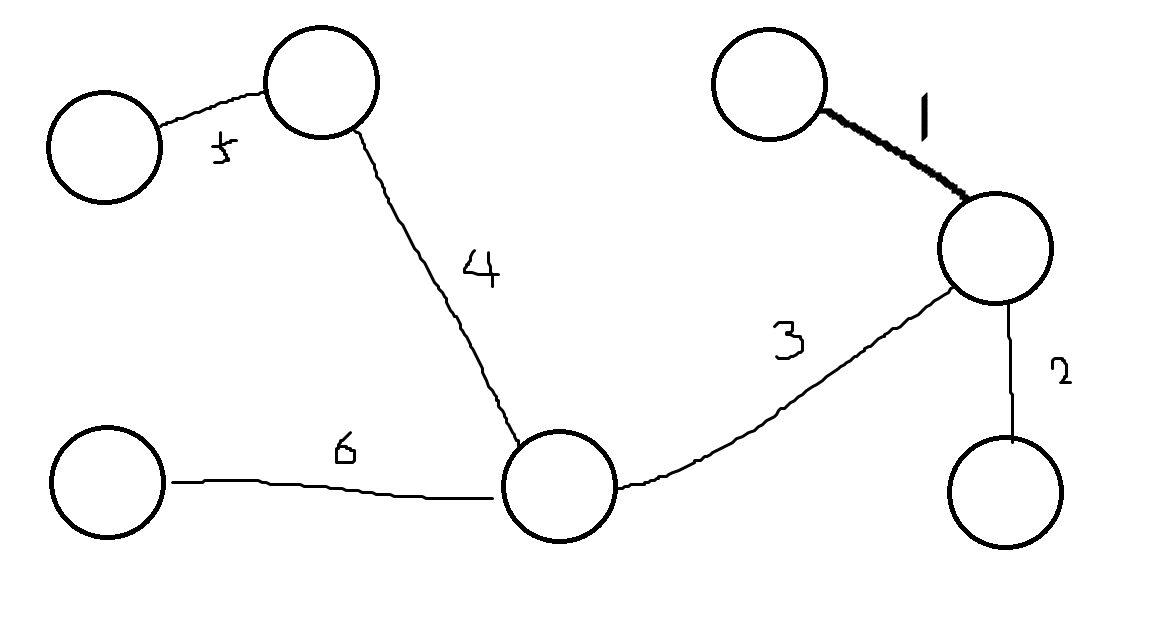
만약 최소 신장 트리가 위와 같이 구성된다면 위 상태에서 마을을 2개로 분할하면 된다.
하지만 마을 유지비가 최소 비용이 되어야 한다.
이 말은 MST에서 최대 비용인 길을 끊어내 마을을 분할시킨다는 뜻이 된다.
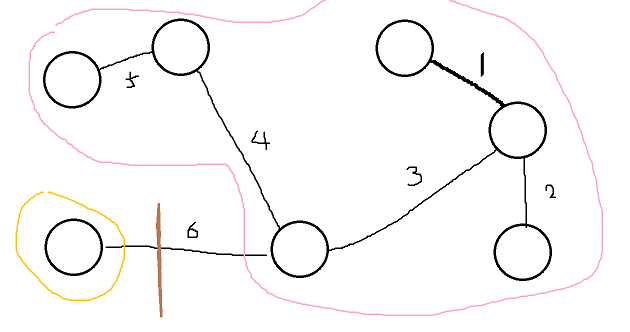
그래서 가장 값이 큰 6인 길을 없애면 마을이 위와 같이 2개로 만들어진다.
그래서 총 유지비는 1+2+3+4+5가 된다.
코드 풀이도 MST 최소 신장 트리를 만들어 비용을 모두 합친 다음 그 중 최대 비용을 빼는 식으로 구하였다.
아래는 크루스칼 알고리즘을 사용하였다.
package _240702;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BOJ_도시분할계획 {
static Edge[] edges;
static int N, M, result;
static int parent[];
static class Edge{
int v1, v2, c;
Edge(int v1, int v2, int c){
this.v1 = v1;
this.v2 = v2;
this.c = c;
}
}
public static void main(String[] args) throws Exception{
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stringTokenizer = new StringTokenizer(bufferedReader.readLine());
N = Integer.parseInt(stringTokenizer.nextToken());
M = Integer.parseInt(stringTokenizer.nextToken());
parent = new int[N+1];
edges = new Edge[M];
for(int i=0;i<M;i++){
stringTokenizer = new StringTokenizer(bufferedReader.readLine());
int A = Integer.parseInt(stringTokenizer.nextToken());
int B = Integer.parseInt(stringTokenizer.nextToken());
int C = Integer.parseInt(stringTokenizer.nextToken());
edges[i] = new Edge(A, B, C);
}
Arrays.sort(edges, (n1, n2) -> n1.c - n2.c);
makeSet();
int cnt = 0;
int max = 0;
for(Edge edge : edges){
if(union(edge.v1, edge.v2)){
result += edge.c;
max = Math.max(max, edge.c);
cnt++;
}
if(cnt == N-1){
break;
}
}
System.out.println(result - max);
}
static void makeSet(){
for(int i=0;i<N;i++){
parent[i] = i;
}
}
static int findSet(int x){
if(parent[x] == x) return x;
return parent[x] = findSet(parent[x]);
}
static boolean union(int x, int y){
int px = findSet(x);
int py = findSet(y);
if(px == py) return false;
if(px < py) parent[py] = px;
else parent[px] = py;
return true;
}
}