백준 11404

문제

---

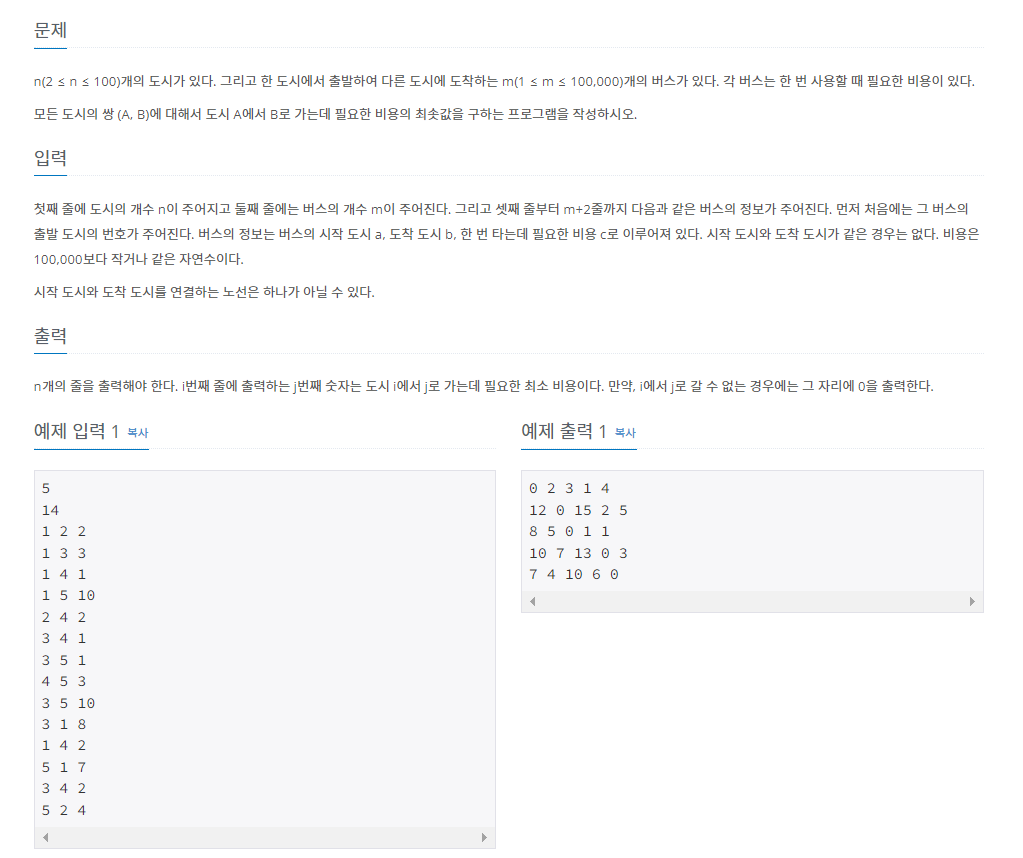
Floyd-Warshall Algorithm

다익스트라 알고리즘은

하나의 지점에서 다른 특정 지점까지의 최단 경로를 구하는 알고리즘

이것을 확장시켜,

모든 두 지점 간의 최단 경로를 모두 구하고 싶을 때

Floyd-Warshall 알고리즘을 쓸 수 있다고 함.

---

모든 두 노드 간의 최단 경로를 구해야하므로

DP로 사용할 2차원 배열을 만든다.

각각의 노드들이 경로의 중간 노드라고 했을 때, 총 거리가 짧아지면 최단거리를 갱신한다.

물론 초기값 INF 은 적당히 큰 값으로 설정한다.

ex) (최대 가중치) * (정점의 개수 - 1) + 1

---

Integer.MAX_VALUE로 설정하면 안된다...

거리 더하는 순간 int 범위상 음수로 바뀌어버리고

Math.min이나 조건문 등으로 더 짧은 거리 저장하라고 명령해 놓았으니

해당 음수가 저장되어 버린다.

---

Code

package test;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.StringTokenizer;

public class P11404 {

	// INF : 최대 가중치 * (정점 개수 - 1) 보다 큰 값으로
	static final int INF = 100000 * (100 - 1) + 1;
	static int[][] dist;
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringBuilder sb = new StringBuilder();
		StringTokenizer st;
		
		int n = Integer.parseInt(br.readLine());
		int m = Integer.parseInt(br.readLine());
		
		dist = new int[n + 1][n + 1];
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= n; j++) {
				/*
				 문제 조건 상
				 자신으로 가는 간선은 없음
				 */
				dist[i][j] = i == j ? 0 : INF; 
			}
		}
				
		for(int i = 0; i < m; i++) {
			st = new StringTokenizer(br.readLine(), " ");
			int a = Integer.parseInt(st.nextToken());
			int b = Integer.parseInt(st.nextToken());
			int c = Integer.parseInt(st.nextToken());
			
			/*
			 동일한 간선에 대해 여러 가중치가 입력되면
			 그 중 가장 작은 값 저장
			 */
			dist[a][b] = Math.min(dist[a][b], c);
		}
		
		floydWarshall(n);
		
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= n; j++) {
				if(dist[i][j] >= INF) {
					// 경로 없을 경우
					dist[i][j] = 0;
				}
				sb.append(dist[i][j]).append(" ");
			}
			sb.append('\n');
		}
		
		bw.write(sb.toString());
		
		br.close();
		bw.flush();
		bw.close();
	}
	
	// int n : 전체 노드(정점) 개수
	private static void floydWarshall(int n) {
		/*
		Round k : 
		k번 노드를 경로의 중간 지점이라 할 때
		i번 노드부터 j번 노드까지 거리가 짧아지면
		최단 거리 갱신   
		*/
		for(int k = 1; k <= n; k++) {
			for(int i = 1; i <= n; i++) {
				for(int j = 1; j <= n; j++) {
					if(dist[i][j] > dist[i][k] + dist[k][j]) {
						dist[i][j] = dist[i][k] + dist[k][j];
					}
				}
			}
		}
	}

}

---

참고 :

https://velog.io/@kimdukbae/%ED%94%8C%EB%A1%9C%EC%9D%B4%EB%93%9C-%EC%9B%8C%EC%85%9C-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Floyd-Warshall-Algorithm

https://chanhuiseok.github.io/posts/algo-50/