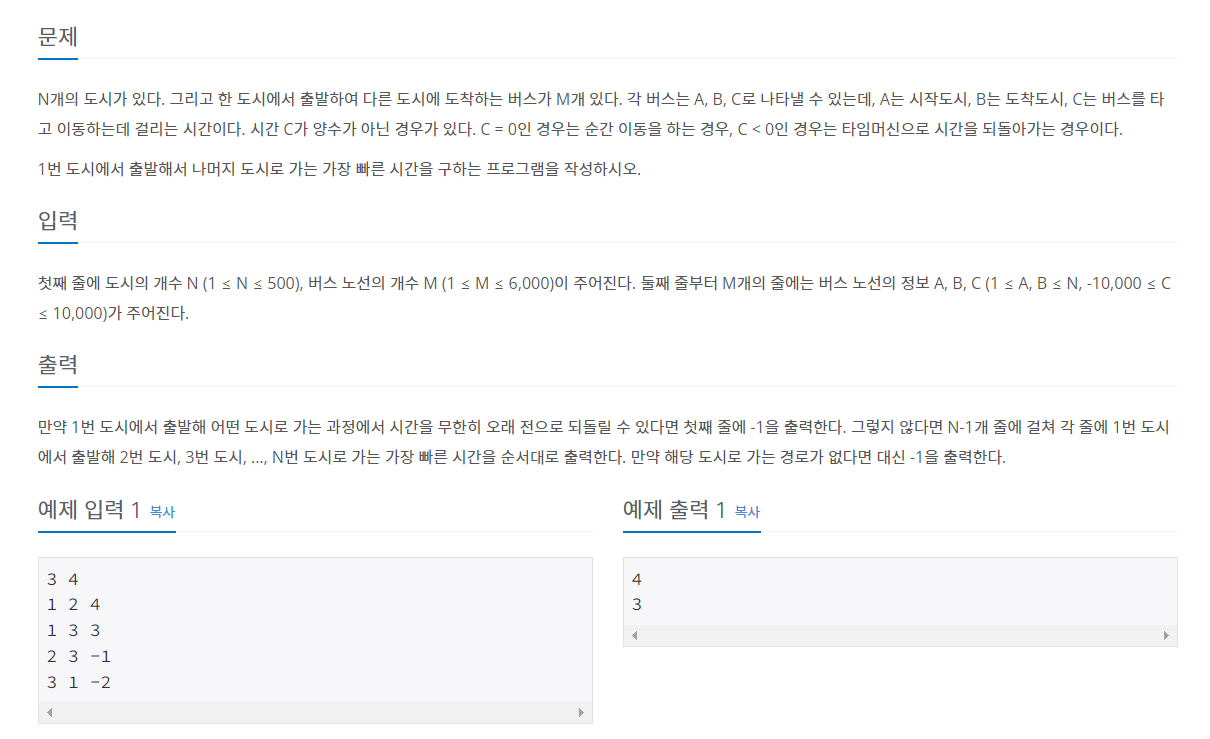
간선의 가중치가 음수일 수 있기 때문에 모든 경우를 다익스트라 알고리즘으로 풀 수 없다.
다익스트라 알고리즘의 경우, 매번 방문하지 않은 노드 중 최단거리가 짧은 노드를 선택하기 때문
이것은 간선의 가중치가 양수라는 전제 하에 가능한 것
2개의 문제를 해결해야 함
문제 1)
만약 음수 가중치가 존재한다면, 다익스트라 알고리즘을 사용해서
각 단계에서는 거리(가중치)가 짧은 노드를 선택했더라도,
결과적으로는 다른 루트가 거리가 더 짧을 수 있다.
(아래의 예시 참고 : 1에서 시작해서 3을 먼저 방문해버리기 때문에 1 -> 3이 정답이 되는 잘못된 결과)
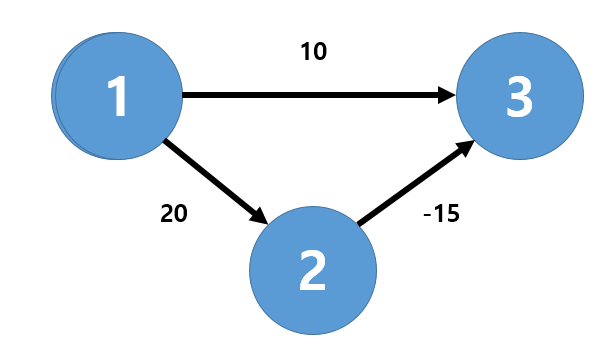
문제 2)
아래의 예시와 같이, 최단 거리를 특정할 수 없는 경우가 있다.
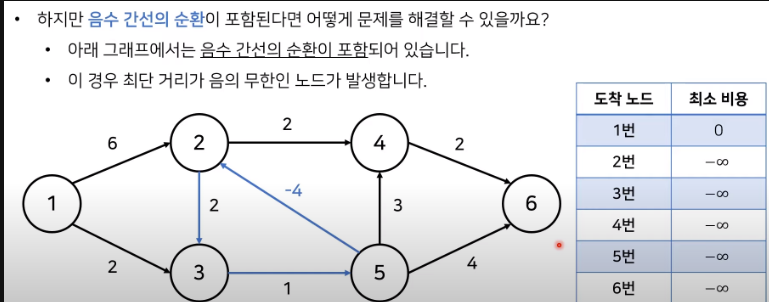
왜냐하면 2,3,5 번 노드가 사이클을 이루고 있고 2 -> 3 -> 5 순으로 이동할 경우
총 거리가 음수(-1)이다.
거기다가 모든 노드가 1에서 출발해서 2 -> 3 -> 5 사이클을 거쳐 도달할 수 있기 때문에
해당 사이클을 많이 거칠수록 최단 거리가 그만큼 줄어들게 됨
위와 같은 사이클을 '음의 사이클'이라고 한다고 함.
따라서 최단 거리 갱신을 하면서도
다익스트라 알고리즘과 다르게
1) 모든 경우의 수를 생각해야 하고
2) 음의 사이클이 존재하는지 파악해야 함
Bellford - Algorithm
음수인 가중치를 가지는 간선이 존재한다면 Bellford-Algorithm으로 해결해야 한다고 함
정점의 개수를 N이라 하자.
결론 : 최단 거리 갱신을 (N - 1) 번 만큼 시행한 후, 다시 최단 거리를 갱신했을 때 결과가 또 변경된다면 음의 사이클이 존재하는 것
먼저 갱신을 (N - 1)번 만큼 하는 이유는,
한 번에 갱신이 모두 안되는 경우가 존재하기 때문
당연한 사실이지만, 음의 사이클이 없을 경우
최단거리를 이루는 간선의 개수는 최대 N - 1 개이다.
1
|
2 <- 3 <- 4 <- 5 <- 6
// 1, 2, 3, 4, 5, 6 순으로 (1번 노드부터의) 최단거리 계산할 때
// 예를 들어, 2번 노드의 경우 한 번에 최단거리 갱신 안 됨.따라서 시작 노드를 제외한 정점의 개수(N - 1)만큼 갱신을 하면 충분하다.
다만, (N - 1) 번 내에 더 이상 갱신되지 않는다면 음의 사이클이 존재하지 않는다는 것이므로
성능을 고려하여 중단해도 무방
Code
package test;
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.StringTokenizer;
public class P11657 {
static class Bus {
int end;
int time;
Bus( int end, int time) {
this.end = end;
this.time = time;
}
}
static ArrayList<ArrayList<Bus>> list;
static final long INF = Long.MAX_VALUE;
static long[] dist; // dist[i]: 1번부터 i번까지의 최단 거리
static int N, M;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringBuilder sb = new StringBuilder();
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
list = new ArrayList<>();
for(int i = 0; i <= N; i++) {
list.add(new ArrayList<>());
}
dist = new long[N + 1];
for(int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine(), " ");
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int C = Integer.parseInt(st.nextToken());
list.get(A).add(new Bus(B, C));
}
if(bellmanFord()) {
sb.append(-1);
} else {
for(int i = 2; i < dist.length; i++) {
long result = dist[i] == INF ? -1 : dist[i];
sb.append(result).append('\n');
}
}
bw.write(sb.toString());
br.close();
bw.flush();
bw.close();
}
// return : 음의 사이클 존재 여부
private static boolean bellmanFord() {
Arrays.fill(dist, INF);
dist[1] = 0;
boolean flag = false; // 최단거리 갱신 여부
for(int i = 1; i < N; i++) {
flag = false;
for(int j = 1; j <= N; j++) {
for(Bus bus : list.get(j)) {
if(dist[j] == INF) {
// 가는 길 없음
break;
}
if(dist[bus.end] > dist[j] + bus.time) {
dist[bus.end] = dist[j] + bus.time;
flag = true;
}
}
}
/*
(정점의 개수 - 1) 번 내에 최단 거리 갱신이 더 이상 일어나지 않는다면
음의 사이클이 없다는 것이므로
성능을 고려하여 중단해도 무방
*/
if(!flag) {
break;
}
}
/*
음의 사이클이 존재한다면
갱신을 하면 또다시 최단거리가 줄어들 것이다.
*/
if(flag) {
for(int i = 1; i <= N; i++) {
for(Bus bus : list.get(i)) {
if(dist[i] == INF) {
break;
}
if(dist[bus.end] > dist[i] + bus.time) {
return true;
}
}
}
}
return false;
}
}
