머신러닝 알고리즘 중 하나인 K-평균(K-means) 군집화 알고리즘에 대해 알아보자.

K-means 알고리즘이란?

머신러닝 비지도학습에 속하는 K-means 알고리즘은 쉽게 말해 데이터를 K개의 군집(Cluster)으로 묶는(Clusting) 알고리즘이다.

군집이란 쉽게 말해서 비슷한 특성을 지닌 데이터들을 모아놓은 그룹(Group)이다. 마찬가지로 군집화는 군집으로 묶는다는 의미로 해석할 수 있다.

K-means 알고리즘에서 K는 묶을 군집(클러스터)의 개수를 의미하고 means는 평균을 의미한다. 단어 그대로의 의미를 해석해보면 각 군집의 평균(mean)을 활용하여 K개의 군집으로 묶는다는 의미다. 여기서 평균(Means)이란 각 클러스터의 중심과 데이터들의 평균 거리를 의미하는데 자세히는 뒤에서 살펴보자.

아래의 그림이 주어졌다고 했을 때 어떻게 군집화를 할 수 있을까?

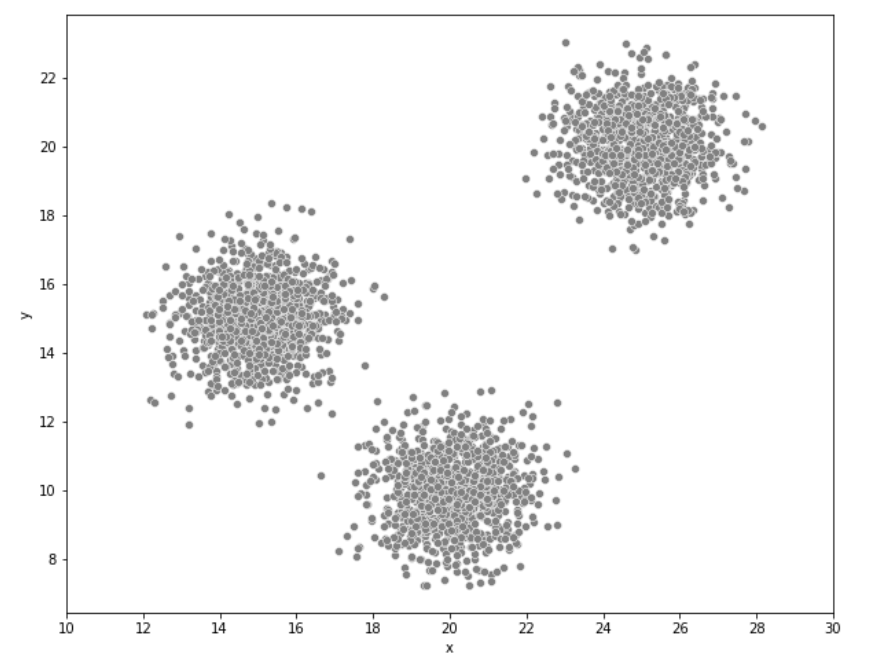
대부분의 사람이라면 아래의 그림과 같이 3개의 군집으로 묶을 것이며 이는 K-means 알고리즘에서 K가 3인 경우에 속한다.

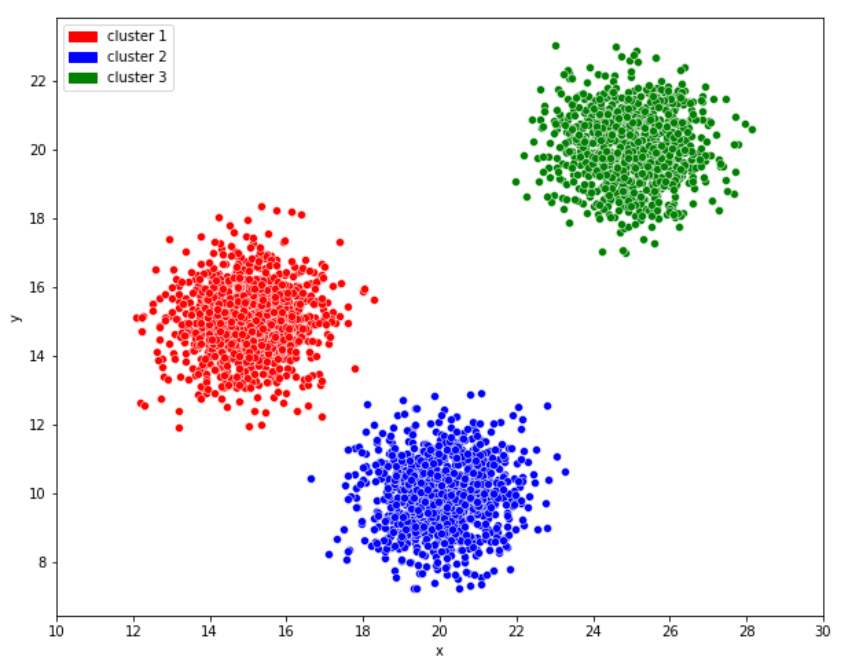
다시 말해, K-means 알고리즘은 비슷한 특성을 지닌 데이터들끼리 묶어 K개의 군집으로 군집화하는 대표적인 군집화 기법이다. 하지만 비슷한 특성을 지닌 데이터들끼리 묶는 방법은 여러가지가 있을 수 있다.

예를 들어 한국, 일본, 중국, 미국, 캐나다, 멕시코, 영국, 독일, 프랑스 총 9개의 국가를 3개의 군집으로 군집화한다고 가정해보자. 이때 이 9개의 국가를 군집화하는 방법은 수 없이 많다. 모국어(제1언어)가 영어인 국가와 아닌 국가로 묶을 수도 있고, 날씨나 인구 수를 기준으로 군집화할 수도 있다. 하지만 K-means 알고리즘을 기반으로는 다음과 같이 군집화 될 것이다.

1) cluster 1

한국	일본	중국

2) cluster 2

미국	캐나다	멕시코

2) cluster 3

영국	독일	프랑스

결과를 보면 아시아 국가들끼리, 북아메리카 국가들끼리, 유럽 국가들끼리 총 3개의 군집으로 묶인 것을 알 수 있다. 이는 거리를 기반으로 군집화한 것이다. 즉, 가까운 나라일수록 비슷한 특성을 지닌 것으로 보고 같은 군집으로 묶은 것이다.

다시 말해, K-means 알고리즘은 가깝게 위치하는 데이터를 비슷한 특성을 지닌 데이터로 여기고 같은 군집으로 군집화한다.
위에서 보았던 그래프에서 점들을 빨간색, 파란색, 초록색, 이 3개의 군집으로 군집화한 것도 결국 거리가 가까운 데이터끼리 군집화한 것이다.

K-means vs K-NN

K-means 알고리즘은 K-NN 알고리즘과 유사하면서도 다르다. 둘은 모두 K개의 점을 지정하여 거리를 기반으로 구현되는 거리기반 분석 알고리즘이다. 하지만 둘의 차이점은 지도학습에 속하는 K-NN 알고리즘과 달리 K-means 알고리즘은 비지도학습 방법에 속한다. 따라서 K-means 알고리즘의 목적을 분류(Classification)라고 하지 않고 군집화(Clustering)라고 한다. 즉, K-NN은 분류 알고리즘, K-means은 군집화 알고리즘이라고 할 수 있다.

이미지 출처 : https://opentutorials.org/course/4548/28942

분류(Classification) vs 군집화(Clustering)

분류와 군집화의 차이점에 대해 간단히 살펴보자.

분류

분류는 지도학습 방법에 속하여 레이블(정답)이 주어졌을 때 레이블을 기반으로 데이터를 나누는 방법을 의미한다. 따라서 머신러닝에서 모델을 학습시킬 때 모델이 제대로 분류하는지를 평가하기 위해 레이블을 제거하고 모델이 예측한 레이블과 실제 레이블을 비교하여 모델의 성능을 판단한다.

군집화

반면, 군집화는 비지도학습 방법에 속하여 레이블(정답)이 주어지지 않았을 때 주어진 데이터를 묶는 방법을 의미한다. 정해진 레이블이 없기 때문에 분류와 달리 어떤 레이블에 속할지 예측하기 보다는 이렇게 묶일(군집화 될) 수 있구나 정도만 파악이 가능하며 이 정보가 필요할 경우 군집화 알고리즘을 사용한다.

K-means 알고리즘 원리 이해하기

K-means 알고리즘을 통해 레이블이 없는 주어진 데이터를 몇 개의 군집으로 묶을 수 있다고 하였는데 이제 실제 어떻게 군집화하는지 K-means 알고리즘의 원리를 알아보자. K-means 알고리즘의 작동 원리는 다음과 같이 5가지 단계로 구성된다. K-means 알고리즘으로 군집화하는 5가지 단계의 과정을 하나씩 살펴보자.

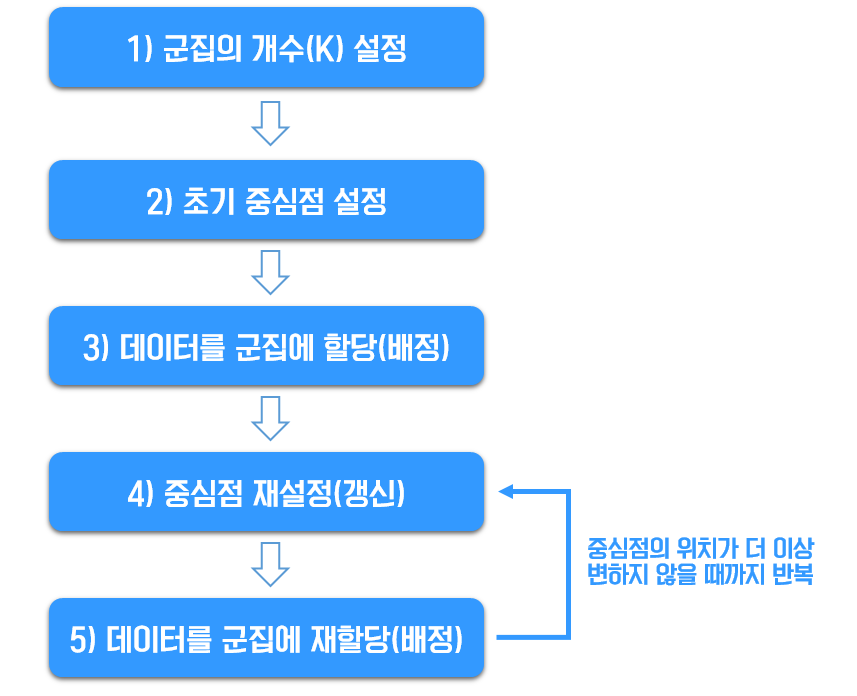
step 1) 군집의 개수(K) 설정하기

데이터를 준비한 뒤 가장 먼저 해야할 것은 군집의 개수를 결정하는 것이다. 몇 개의 군집으로 군집화할지는 사람이 정해야한다. 이는 K-means 알고리즘의 한계점 중에 하나로 보기도 하는데 군집의 개수 설정을 어떻게 하냐에 따라 결과가 크게 달라지며 터무니 없는 결과가 나올 수도 있다는 것이다. 그래서 군집의 개수를 설정하는 방법론으로 다음과 같은 몇 가지 방법들이 존재한다.

1) Rule of thumb
2) Elbow Method
3) 정보 기준 접근법 (Information Criterion Approach)

참고 : Wikipedia(위키피디아)

step 2) 초기 중심점 설정하기

그 다음 K개의 초기 중심점(Center of Cluster, Centroid)을 설정하는 단계이다. 중심점은 영어로 'Centroid'라고 표현하며 이는 무게중심을 뜻한다.

k-means 알고리즘은 초기 중심점으로 어떤 값을 선택하는가에 따라 성능이 크게 달라지는 성질을 가지고 있다고 한다. 따라서 초기 중심 값을 잘 설정해야하며 다음과 같은 몇가지 방법들이 있다.

1) Randomly select
2) Manually assign
3) K-means++

랜덤하게 설정하거나 사람이 임의로 값을 설정해도 되지만 K-means 알고리즘에서 실제 사용되는 초기 중심값 설정 방법은 K-means++ 기법이라고 한다.

step 3) 데이터를 군집에 할당(배정)하기

그 다음 거리 상 가장 가까운 군집(중심점)으로 주어진 모든 데이터를 할당 또는 배정한다.

step 4) 중심점 재설정(갱신)하기

모든 주어진 데이터의 군집 배정이 끝나면 군집의 중심점(Centroid)을 그 군집의 속하는 데이터들의 가장 중간(평균)에 위치한 지점으로 재설정한다.

step 5) 데이터를 군집에 재할당(배정)하기

step 3에서 했던 방법과 똑같이 시행하며, 더 이상 중심점의 이동이 없을 때까지 step 4와 step 5를 반복한다.

K-means 알고리즘 원리 확인하기

앞서 살펴본 K-means 알고리즘의 원리를 단계별로 이해한 뒤 이제 실제 그림으로 각 단계를 확인해보자.

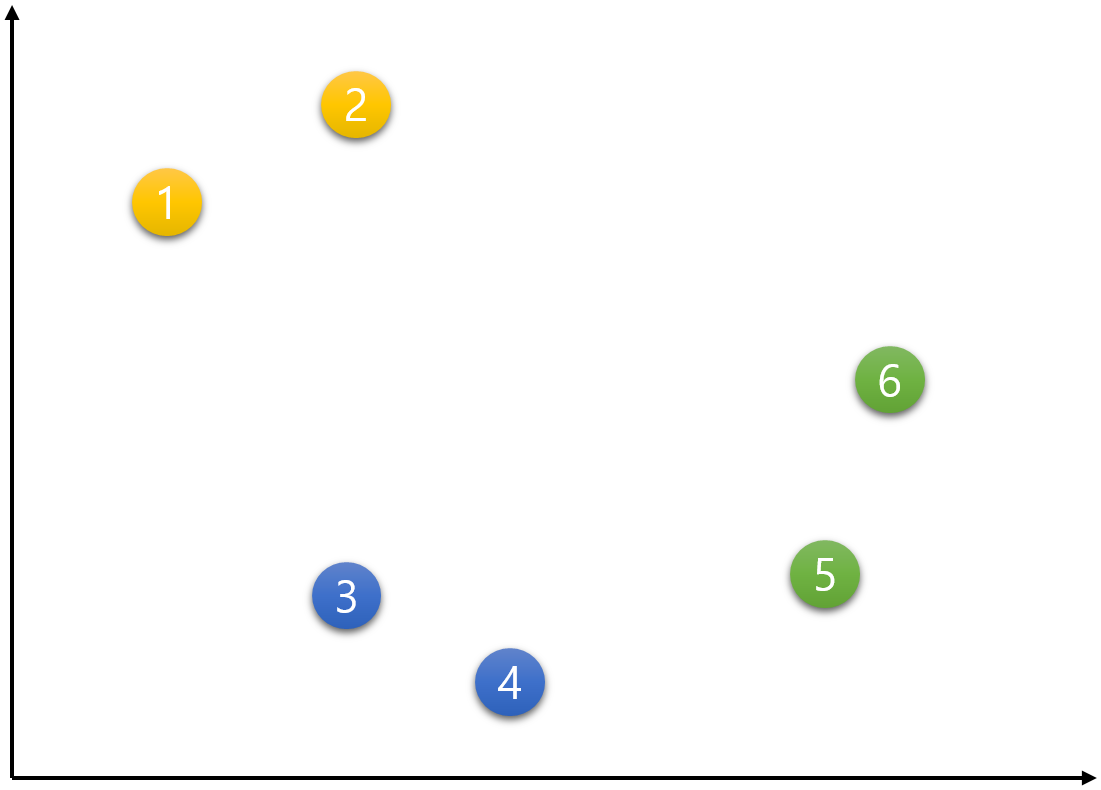
다음과 같이 6개의 데이터가 주어졌다고 하자. 이 주어진 데이터를 K-means 알고리즘의 작동 과정에 따라 군집화 해보자.

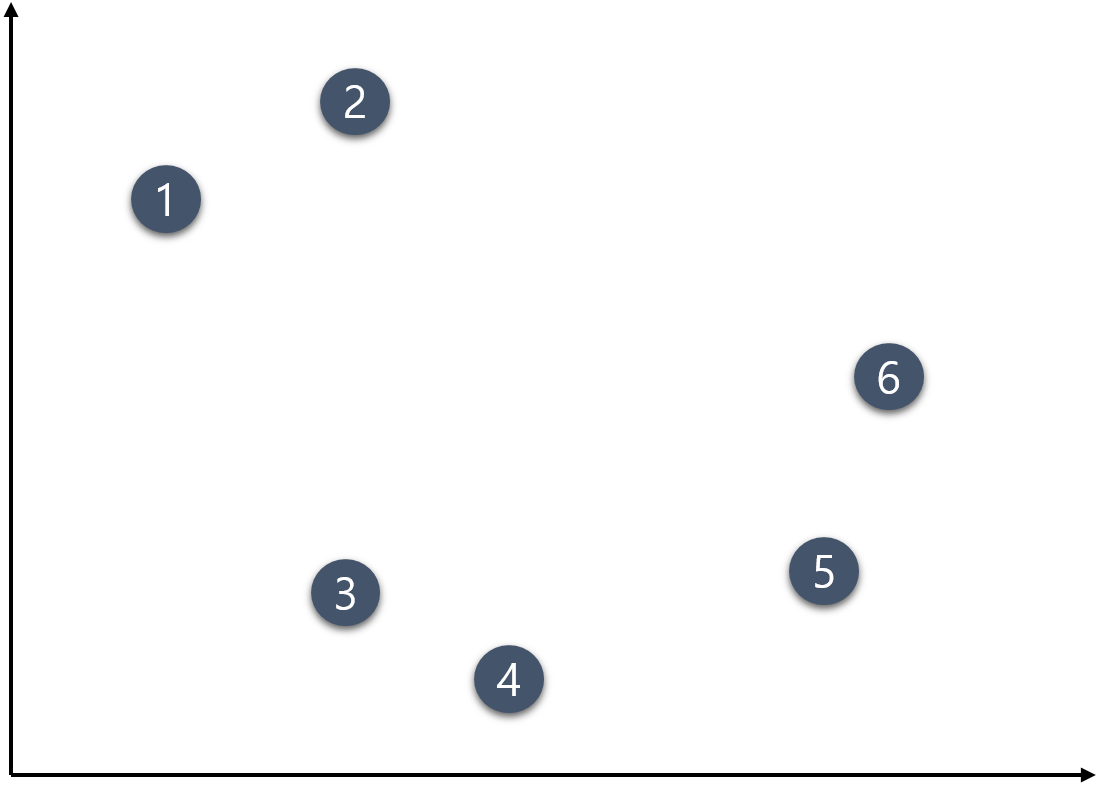
step 1) 군집의 개수(K) 설정하기

군집의 개수는 K는 임의대로 3으로 설정하기로 하자.

step 2) 초기 중심점 설정하기

여러가지 설정 방법이 있지만 여기서는 편의상 초기 중심점(Centroid) c1, c2, c3는 다음과 같이 랜덤으로 설정한다.

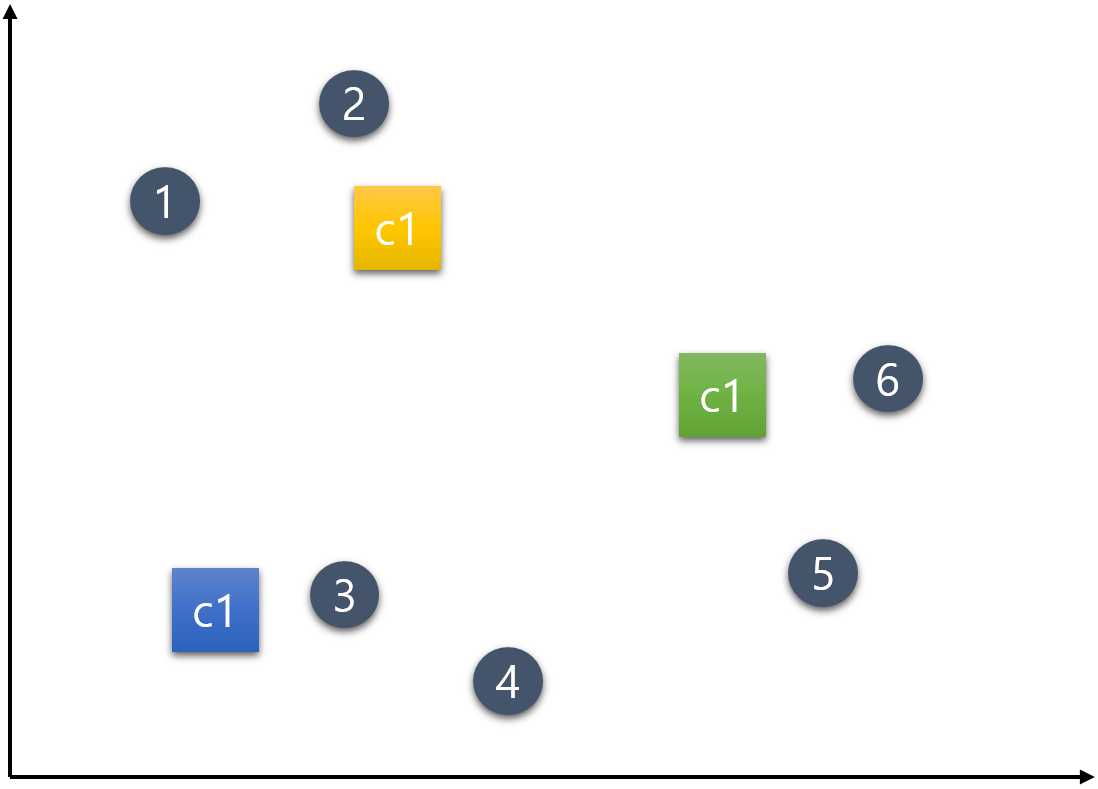
step 3) 데이터를 군집에 할당(배정)하기

거리 상 가장 가까운 군집(중심점)으로 주어진 데이터를 할당 또는 배정하는 단계이며 거리 측정 방법은 일반적으로 유클리드 거리로 측정한다.

1번 데이터부터 시작해서 6번 데이터까지 각각의 중심점에 가까운 군집으로 배정한다.

1번 데이터.

아래의 그림과 같이 c1, c2, c3 중심점으로부터 1번의 유클리드 거리를 측정한다.

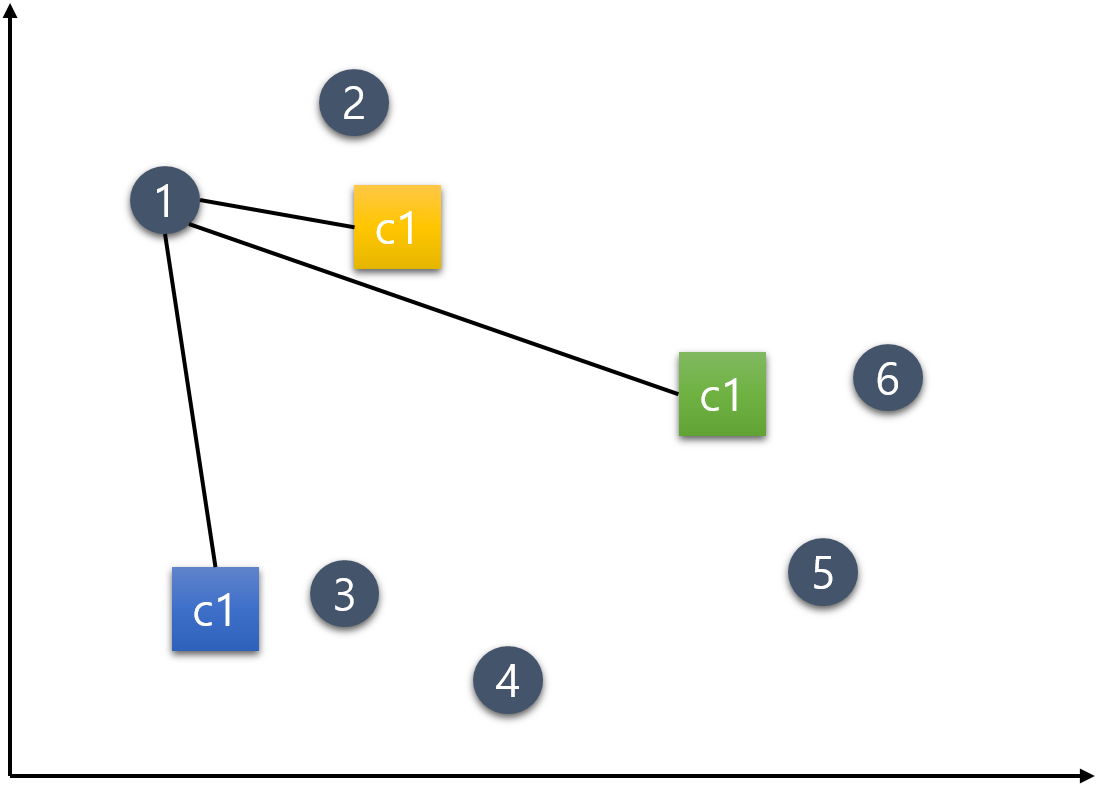
가장 가까이 위치하는 중심점의 군집으로 배정한다. 1번 데이터의 경우 c1 중심점과 가장 가까우므로 노란색으로 바뀐다.

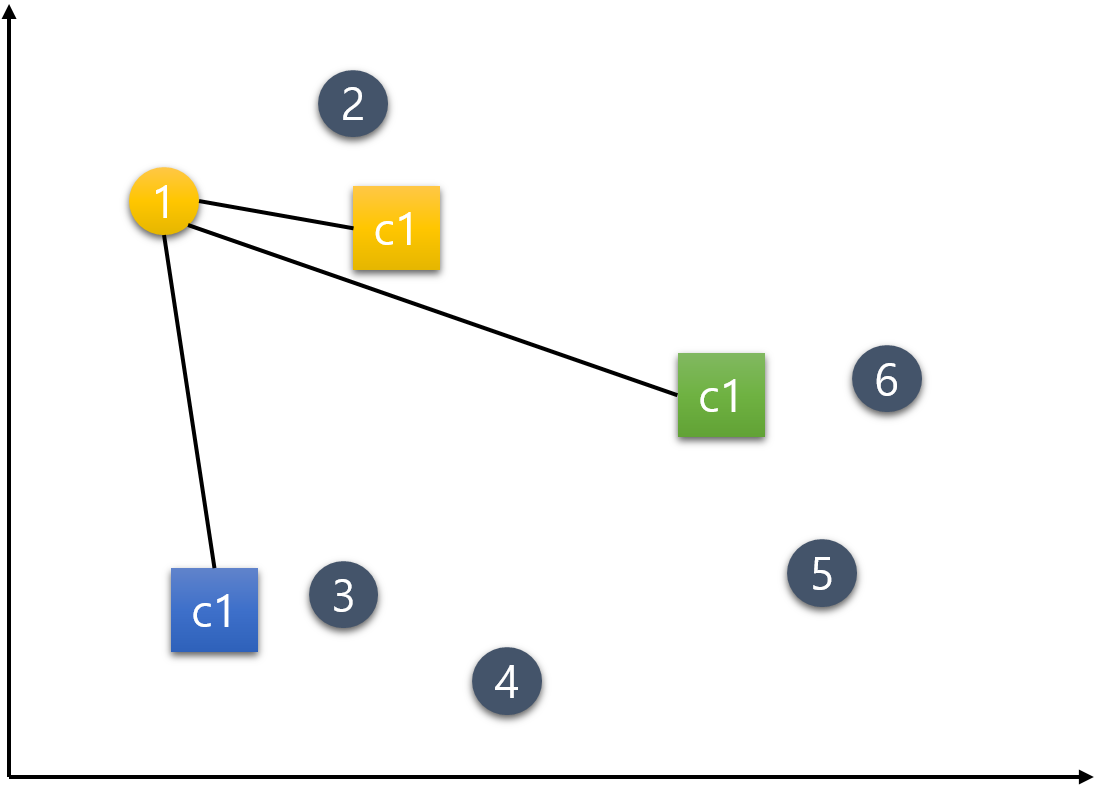
1번 외 나머지 데이터들도 같은 방식으로 배정한다.

2번 데이터.

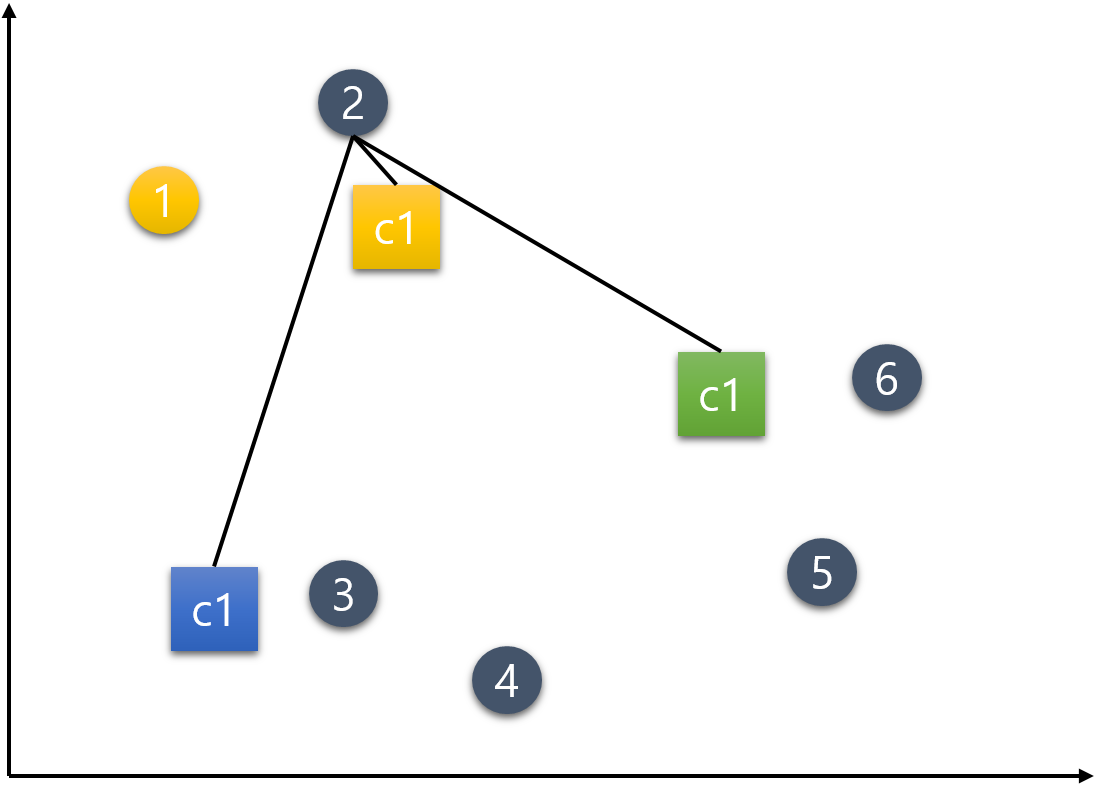
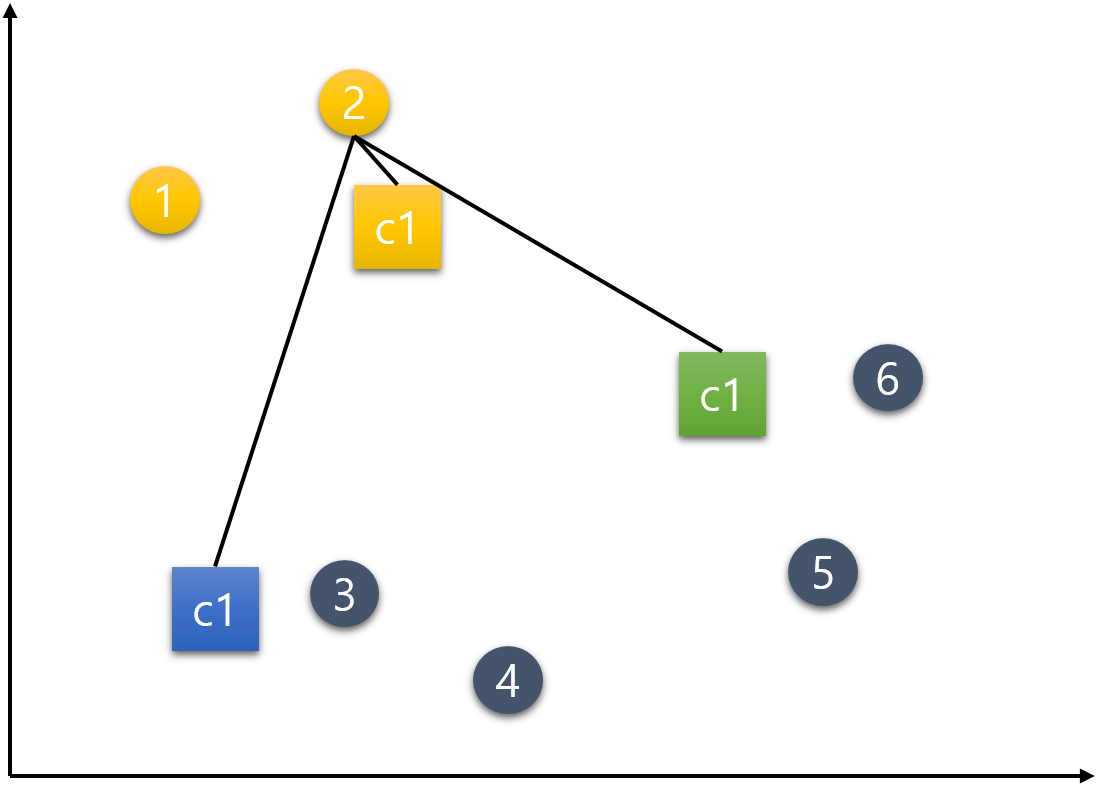
3번 데이터.

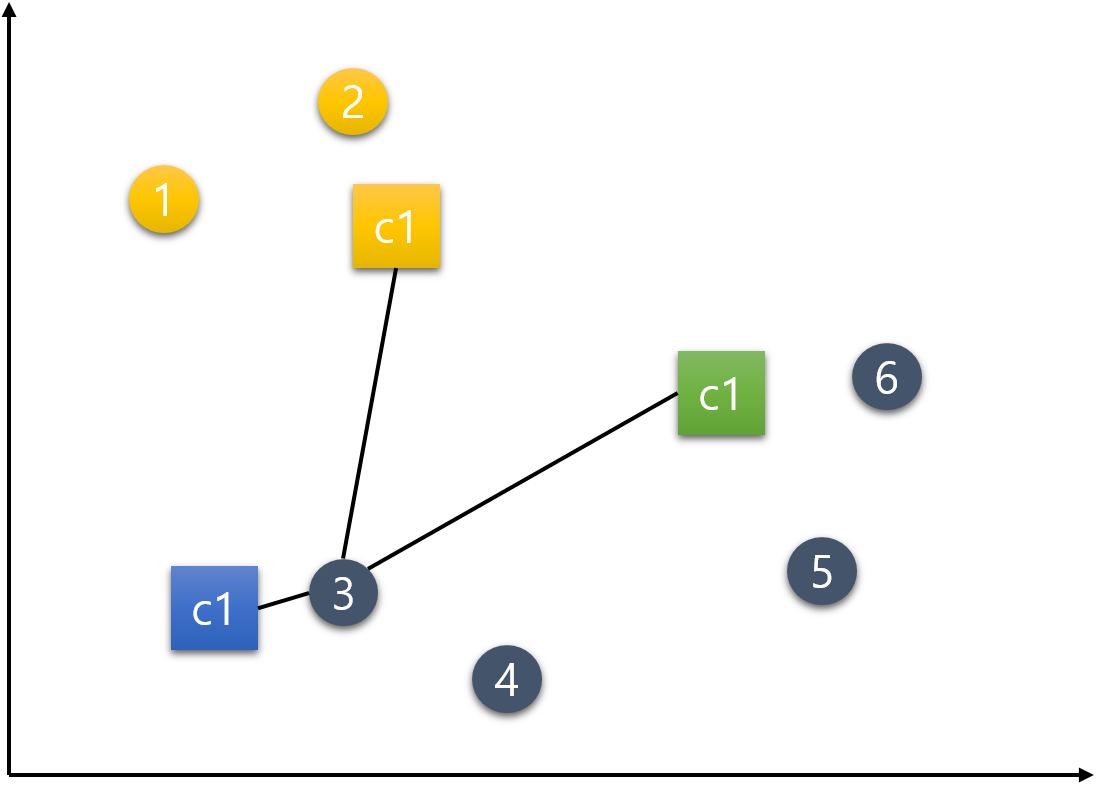
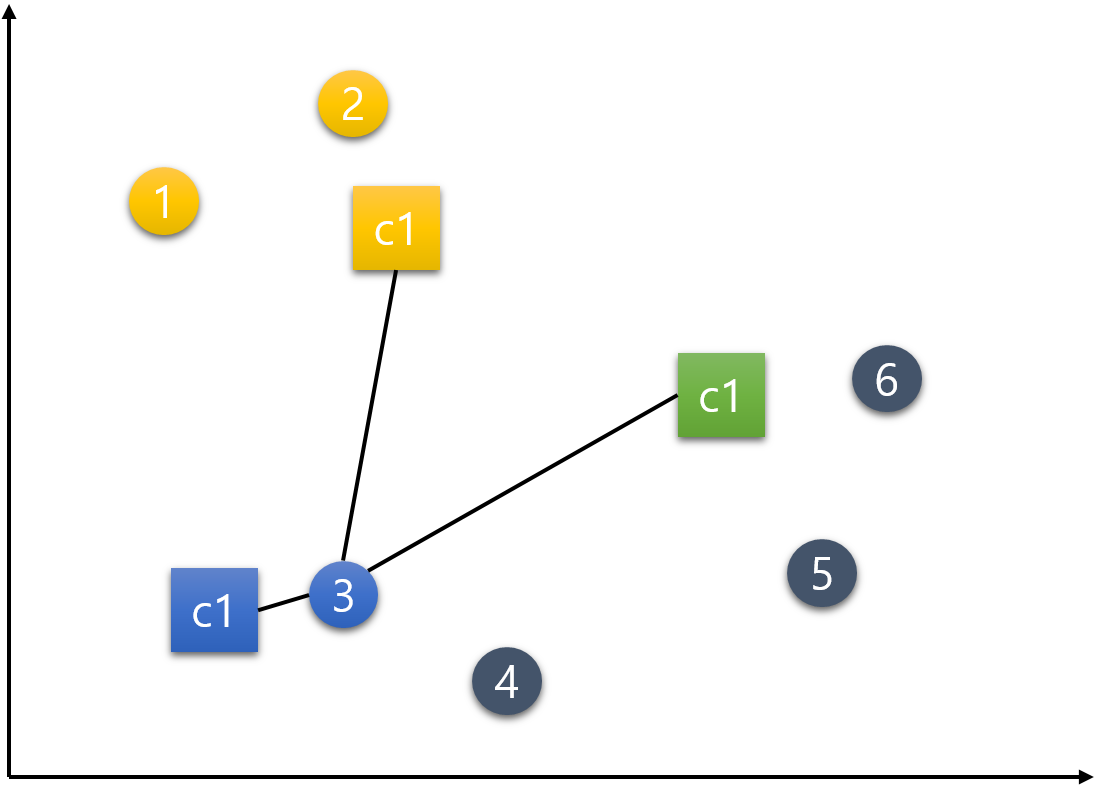
4번 데이터.

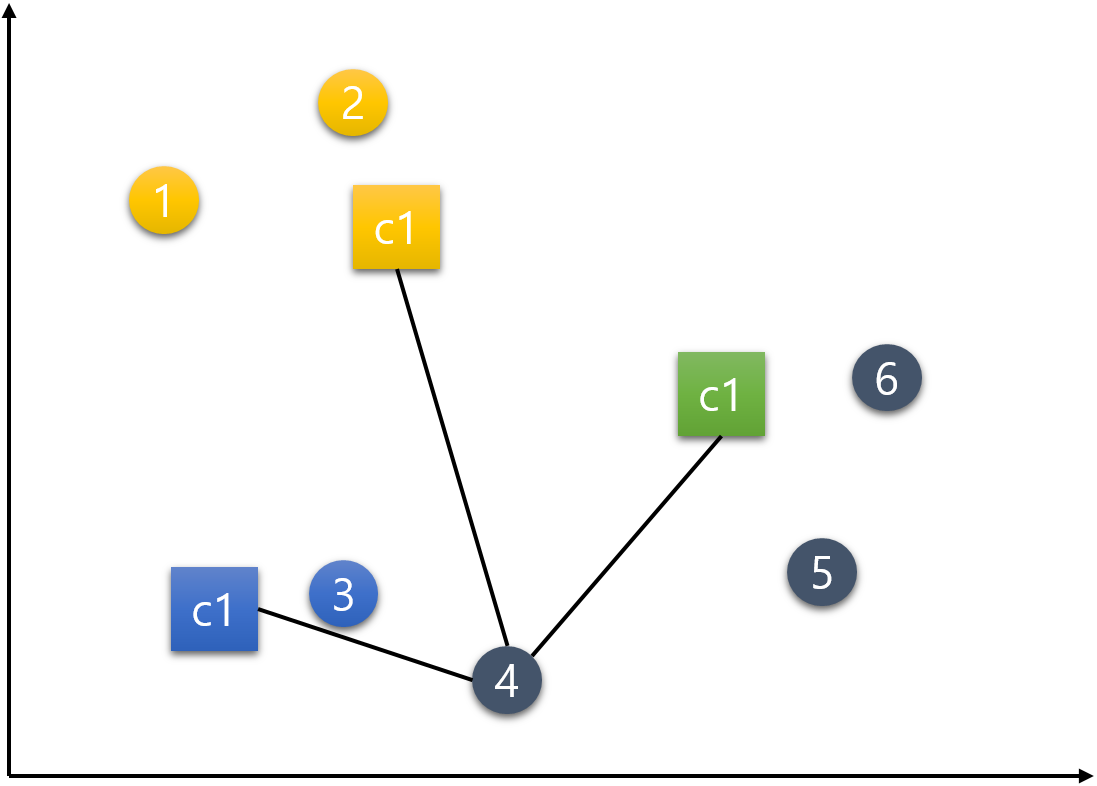
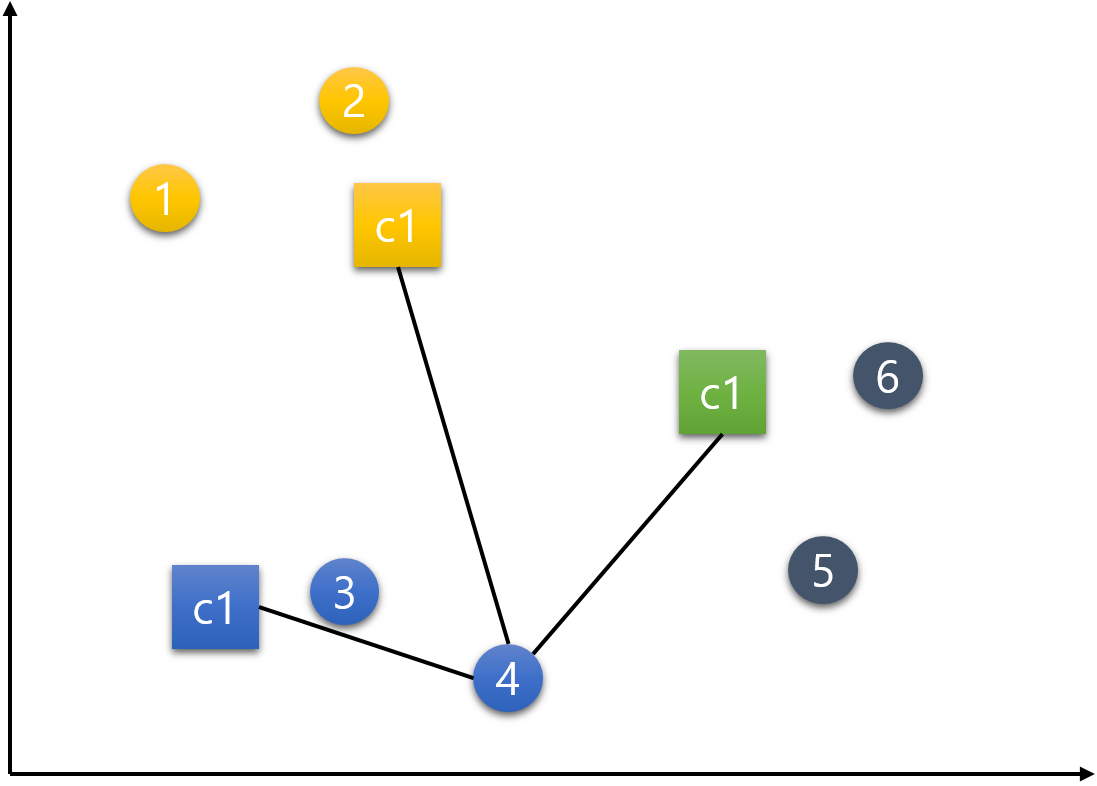
5번 데이터.

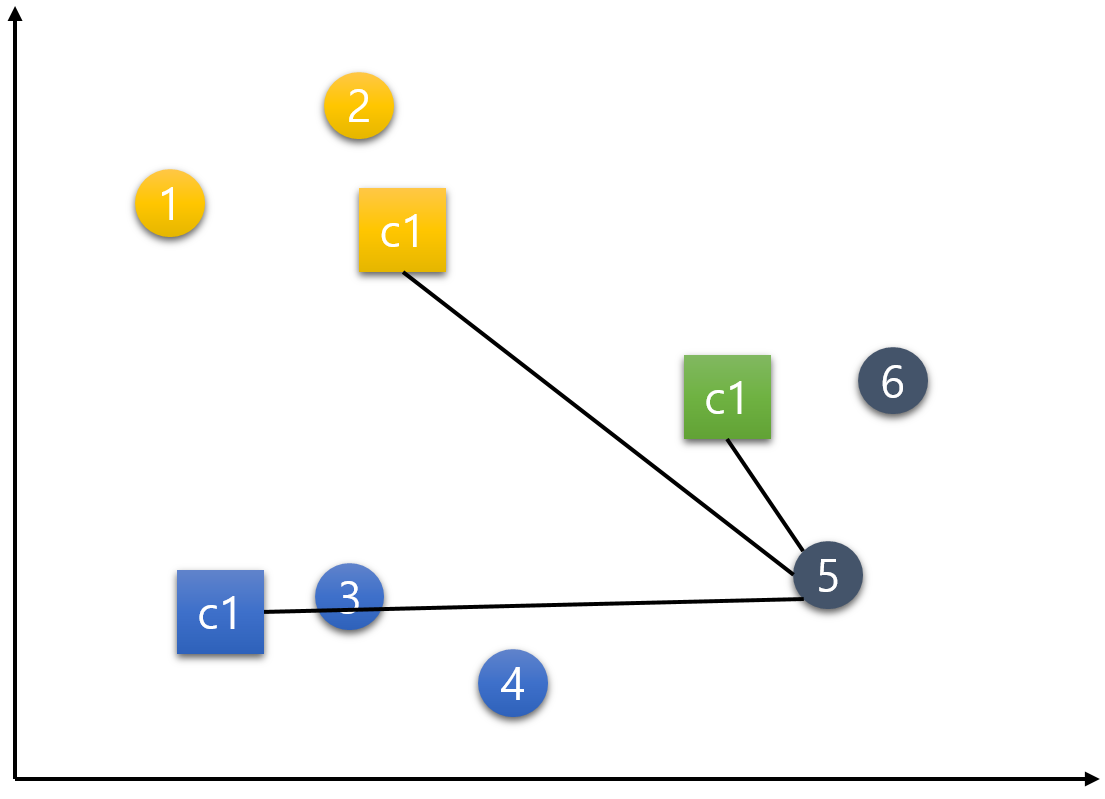
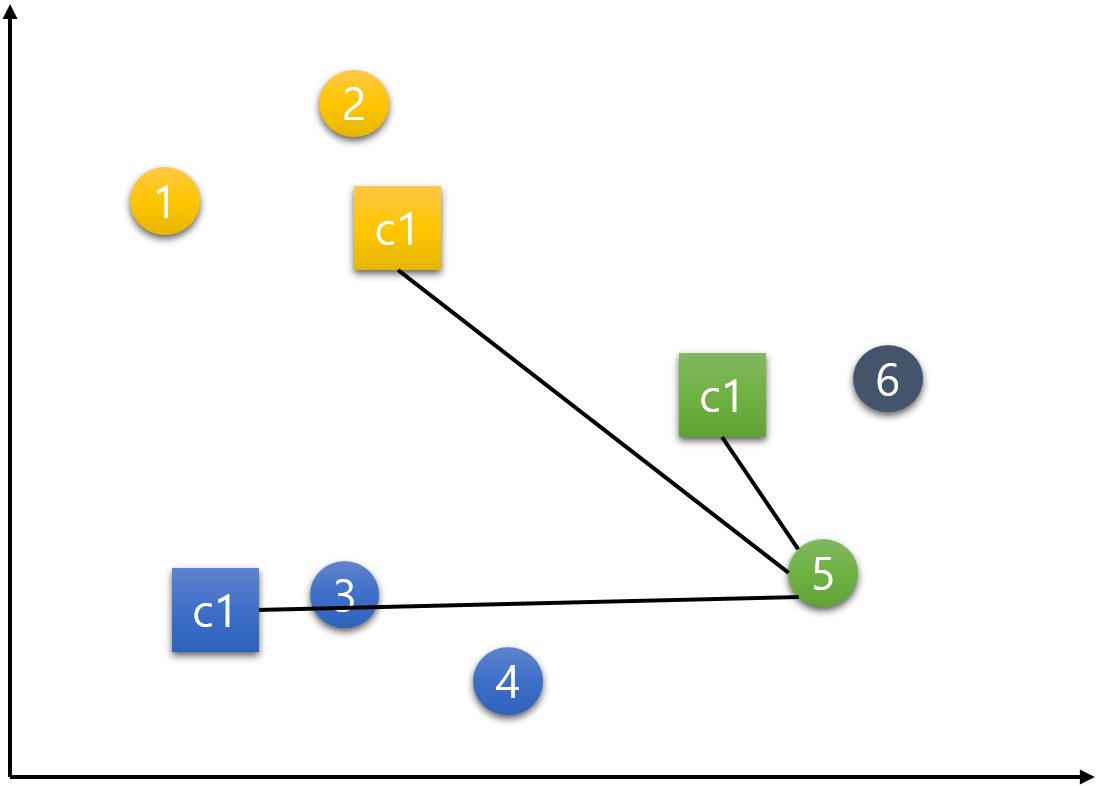
6번 데이터.

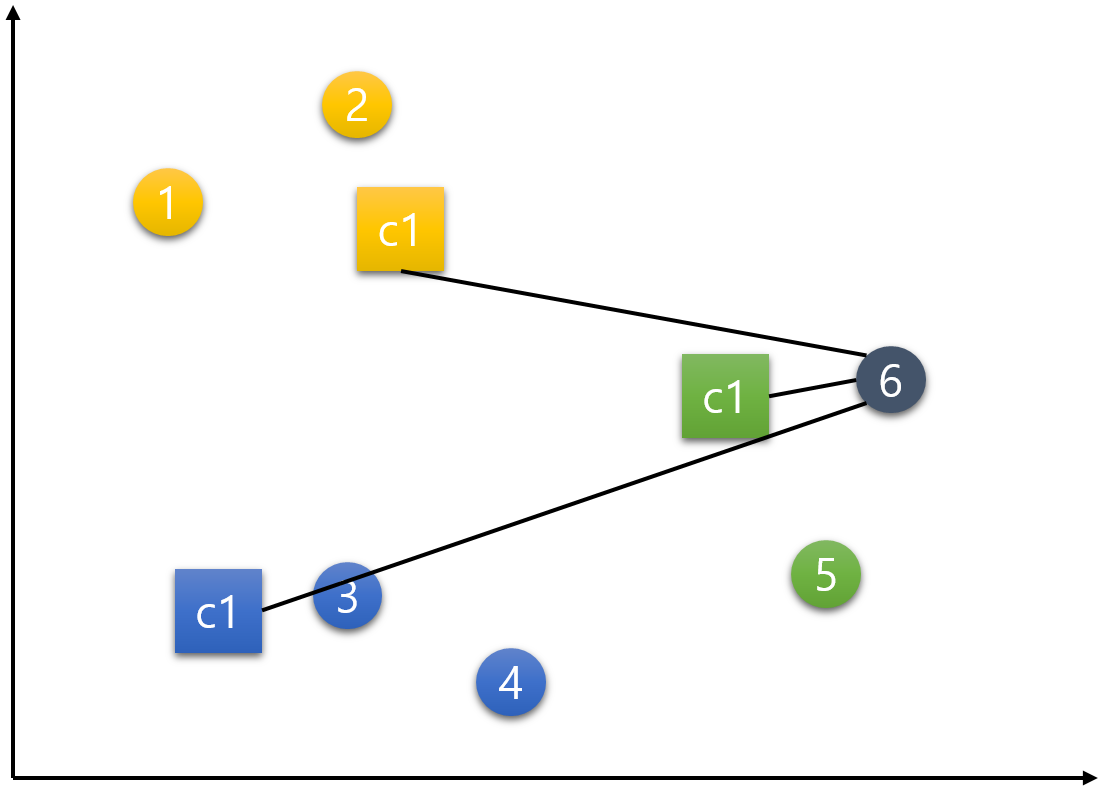
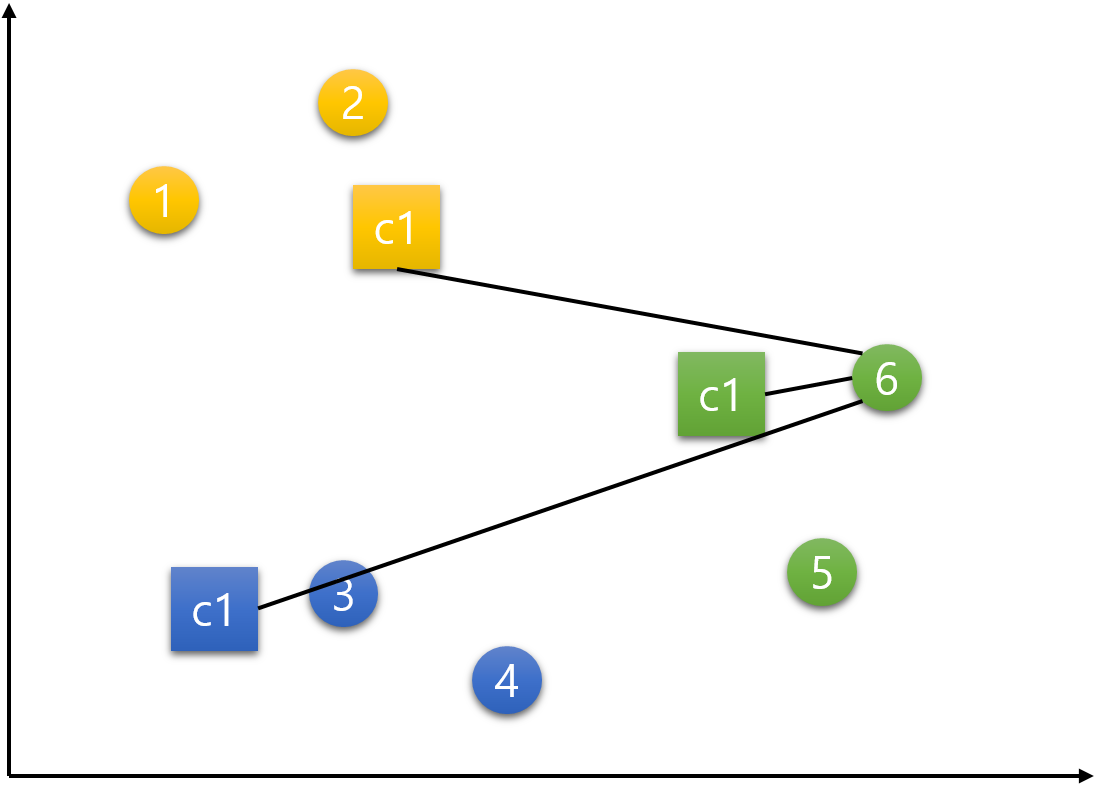
이제 모든 데이터들이 한 번씩 각각의 군집들로 배정이 되었다.

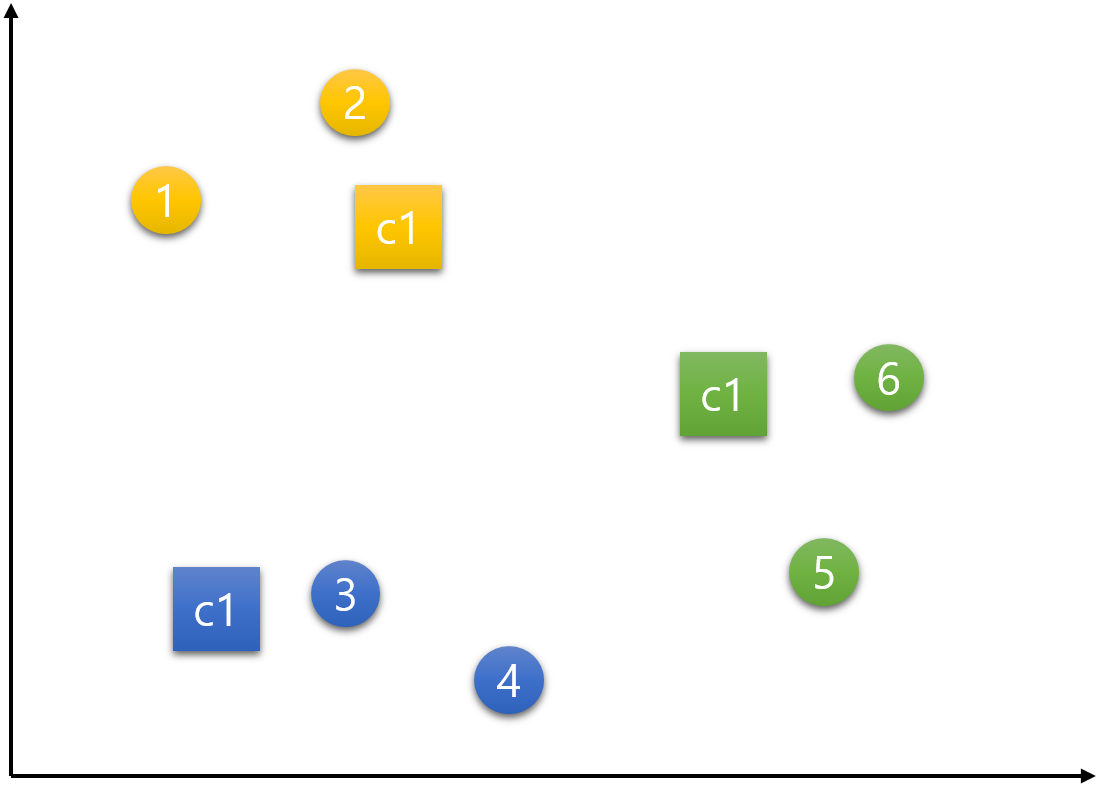
step 4) 중심점 재설정(갱신)하기

이제 중심점을 재설정하는 단계이다.

c1, c2, c3 각각의 중심점은 그 군집의 속하는 데이터들의 가장 중간(평균)에 위치한 지점으로 재설정한다. 중심점 c1은 데이터 1, 2의 평균인 지점으로, 중심점 c2는 데이터 3, 4의 평균인 지점으로, 중심점 c3는 데이터 5, 6의 평균인 지점으로 갱신된다.

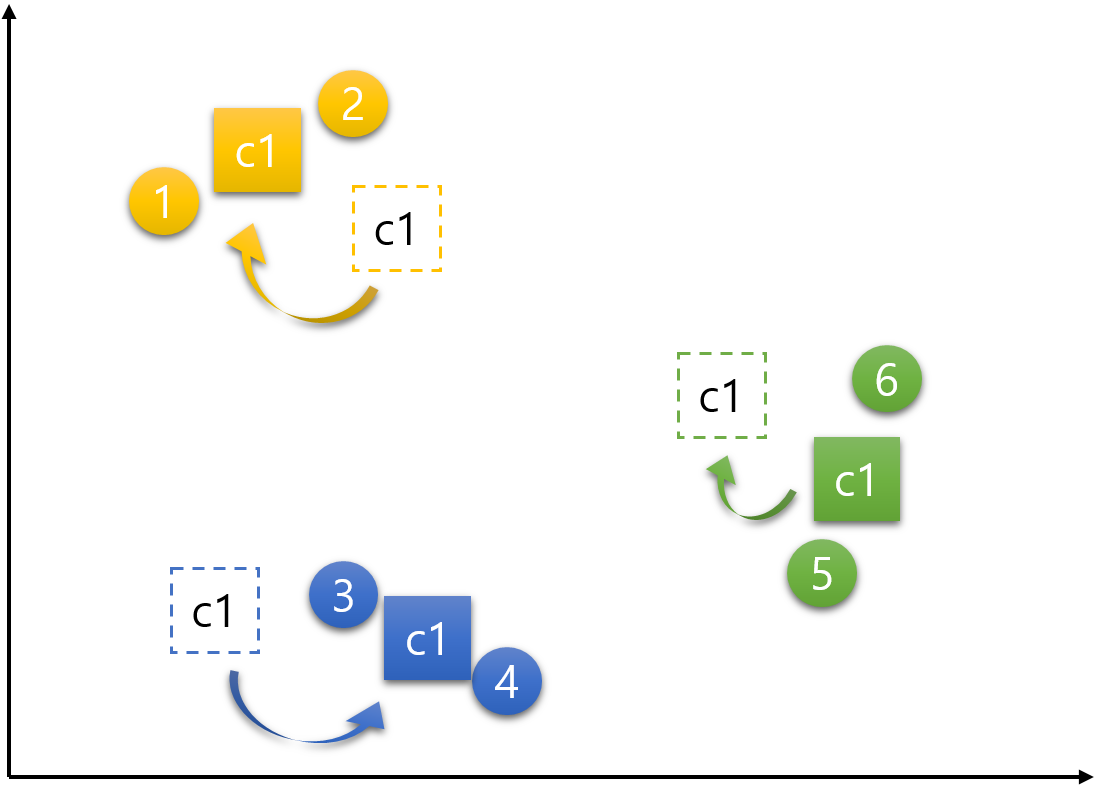
결국 다음과 같이 중심점들이 옮겨진다.

이 세 점이 무게중심을 의미하는 Centroid 라고 불리는 이유는 데이터들의 무게중심의 위치로 이동하기 때문임을 알 수 있다.

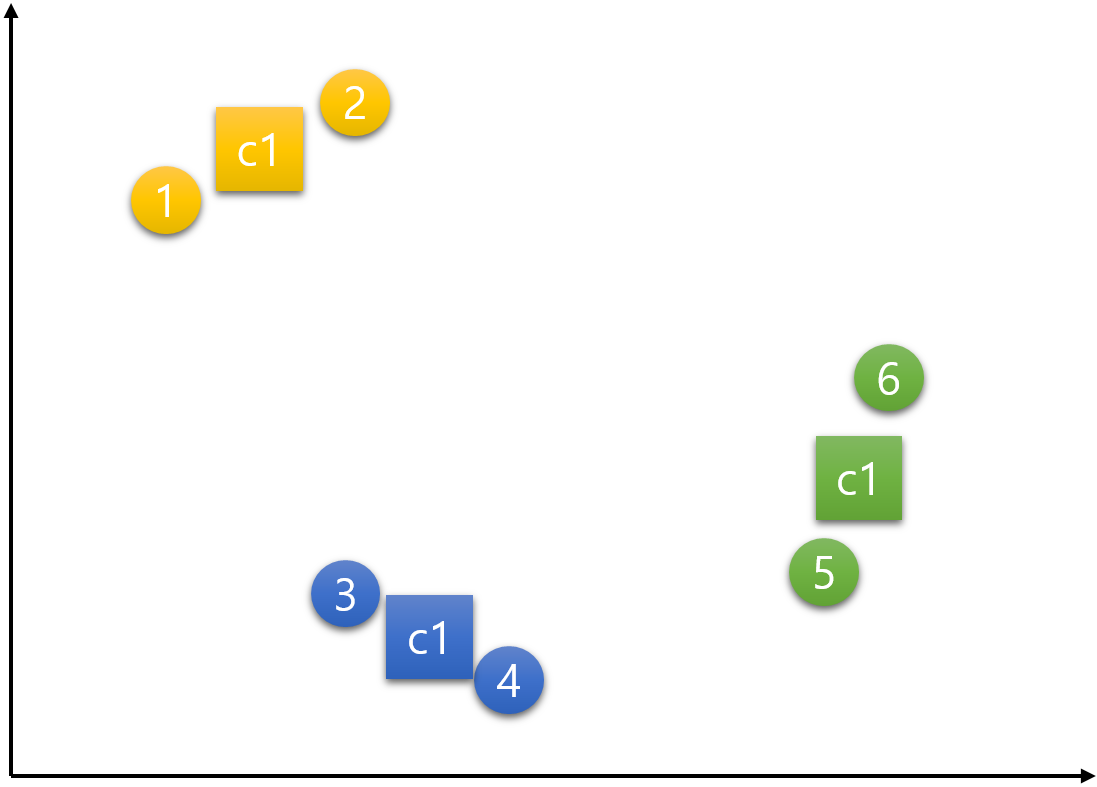
step 5) 데이터를 군집에 재할당(배정)하기

더 이상 중심점의 이동이 없을 때까지 step 4와 step 5를 반복한다고 했는데 위의 예시는 더 이상 이동이 없어 종료된다. 즉, 아래의 그림이 최종 결과이다.