[머신러닝] K-NN(K-Nearest Neighbor) 알고리즘

지도학습에 속하는 K-NN 알고리즘

K-NN 알고리즘은 머신러닝 알고리즘 중 지도학습에 속한다. 지도학습이란 쉽게 말하여 레이블(정답)을 주고 학습을 시키는 것을 의미한다.

예를 들어, 이미지를 주고 개와 고양이를 분류하는데 각각의 이미지가 어떤 레이블에 속하는지 즉, 개인지 고양이인지 꼬리표를 붙혀놓고 학습을 시킨 뒤 기계가 정답을 맞췄는지 확인하는 학습 방식이다.

지도학습은 크게 회귀(Regression)와 분류(Classification)로 나뉘는데 본 글에서 살펴볼 KNN 알고리즘은 지도학습 중 분류에 속한다.

이미지 출처 : https://opentutorials.org/course/4548/28942

지도학습에 속하는 알고리즘은 다음과 같이 다양하다.

• 나이브 베이즈(Naive Bayes)
• 의사결정트리(Decision Trees)
• 최근접 이웃(Nearest Neighbors)
• 선형 회귀(Linear Regression)
• 서포트 벡터 머신(Support Vector Machines)

나머지는 다음에 살펴보고 오늘은 K-NN 알고리즘에 대해 알아보자.

K-NN 알고리즘이란?

K-NN 알고리즘을 설명할 때 대부분 "유유상종"이라는 말을 많이 인용한다. 유유상종이란

"같은 날개를 가진 새들끼리 함께 모인다"

라는 뜻의 속담이다. 즉, 비슷한 특성이나 속성을 가진 것들끼리 가깝게 모여있다는 것이다.
K-NN 알고리즘은 이처럼 데이터를 가장 가까운 속성에 따라 분류하여 레이블링을 하는 알고리즘이다. K-NN은 K-Nearest Neighbor의 줄임말인데, 말 그대로 K개의 가까운 이웃의 속성에 따라 분류한다.

거리기반 분류분석 모델

앞서 가까운 속성에 따라 분류한다고 했는데 '가깝다'는 것에는 기준이 필요하다. K-NN 알고리즘은 거리기반 분류분석 모델로 거리를 기반으로 분류하는 알고리즘이며 따라서 상대적으로 거리가 더 짧은 이웃이 더 가까운 이웃으로 취급된다. 즉, K-NN 알고리즘은 어떤 새로운 데이터로부터 거리가 가까운 K개의 다른 데이터의 레이블(속성)을 참고하여 K개의 데이터 중 가장 빈도 수가 높게 나온 데이터의 레이블로 분류하는 알고리즘이다.

거리 측정 방법

1. 유클리드 거리(Euclidean Distance)

거리 측정 방식에는 여러 가지 방법들이 있겠지만 K-NN 알고리즘은 거리를 측정할 때 일반적으로 '유클리드 거리(Euclidean Distance)' 계산법을 사용한다. 2차원 평면에 서로 다른 두 점 A(x1, y1)와 B(x2, y2)가 있을 때 이 둘의 거리 d는 유클리드 거리 계산법에 의해 다음과 같이 나온다.

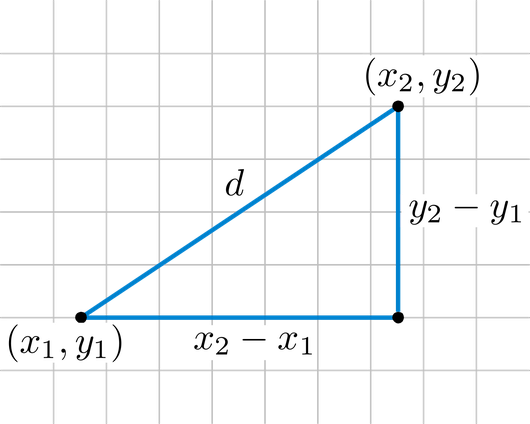
이미지 출처 : https://needjarvis.tistory.com/454

2. 맨해튼 거리(Manhattan Distance)

맨해튼 거리(Manhattan Distance) 혹은 맨하탄 거리는 유클리드 거리(Euclidean Distance)와 함께 매우 기초적인 좌표 간의 거리를 구하는 방식이다. 이 또한 K-NN 알고리즘 내부의 거리 측정 방법으로 흔히 사용된다.

맨해튼 거리의 맨해튼은 실제 미국 뉴욕시의 행정구역 이름이다. 사각형 모양의 촘촘히 들어선 빌딩과 건물의 모습을 지니고 있는 맨해튼의 거리 모습에서 맨해튼 거리 공식이 유래되었다. 유클리드 공식처럼 직선으로 이동할 수 없는 건물들이 많은 체계적인 지역에서 거리를 재기 위해 탄생한 공식으로 보인다.

아래의 그림은 맨해튼 거리를 설명하기에 매우 유용한 그림이다. 검은색 두 점의 거리를 측정하려 한다. 초록색 직선이 바로 위에서 말한 유클리드 거리이다. 바로 검은색 두 점 사이의 최단거리이다. 그리고 나머지 빨간색, 파란색, 노란색 선이 맨해튼 거리를 의미한다. 이 세 선이 모두 맨해튼 거리라는 것은 모두 총 거리가 동일하다는 것이며 이는 실제로 자명한 사실이다.

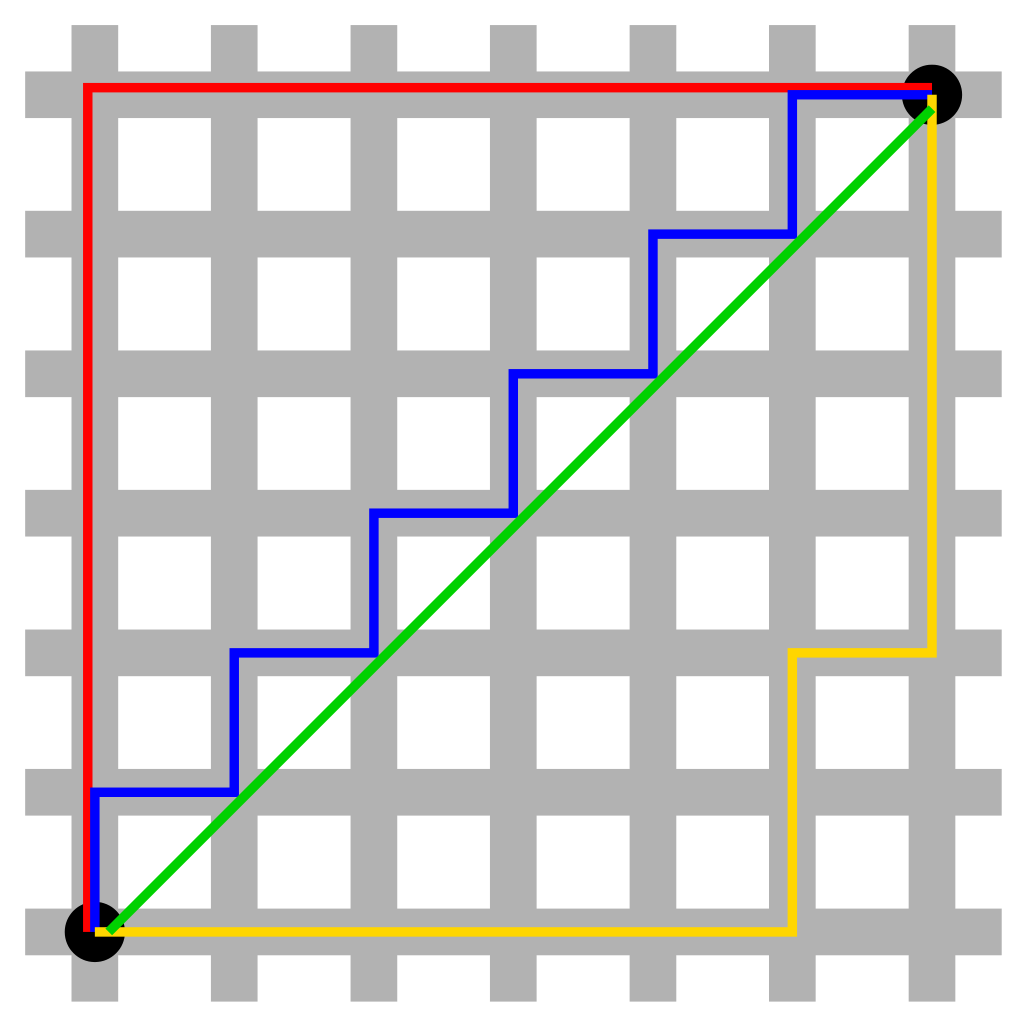
이미지 출처 : https://ko.wikipedia.org/wiki/%EB%A7%A8%ED%95%B4%ED%8A%BC_%EA%B1%B0%EB%A6%AC

위 그림 처럼 2차원 평면에 서로 다른 두 점 A(x1, y1)와 B(x2, y2)가 있을 때 이 둘의 맨해튼 거리(d) 공식은 다음과 같다.

3. 이 외의 거리 측정 공식들

위에서 설명한 유클리드 거리는 다른 말로 L2 Distance라고도 불리며 맨해튼 거리는 L1 Distance라고 불린다. 이들 외에도 해밍 거리(Hamming distance) 등등 자주 사용하지는 않는 여러 거리 측정 방식이 있다.

K-NN 알고리즘의 원리

K-NN 알고리즘의 원리를 이해해야 제대로 이 알고리즘에 대해 파악했다고 할 수 있다. 사실 작동방식이 매우 간단하다. 쉬운 예시를 들어 이해해보자.

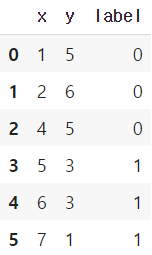
위와 같이 데이터는 총 6개가 있고 변수에 x와 y가 있다. 그리고 각각의 데이터에는 레이블 값이 있다.(K-NN 알고리즘은 앞서 말했듯이 지도학습이기 때문이다.) 위의 데이터를 그래프를 그려보면 다음과 같다.

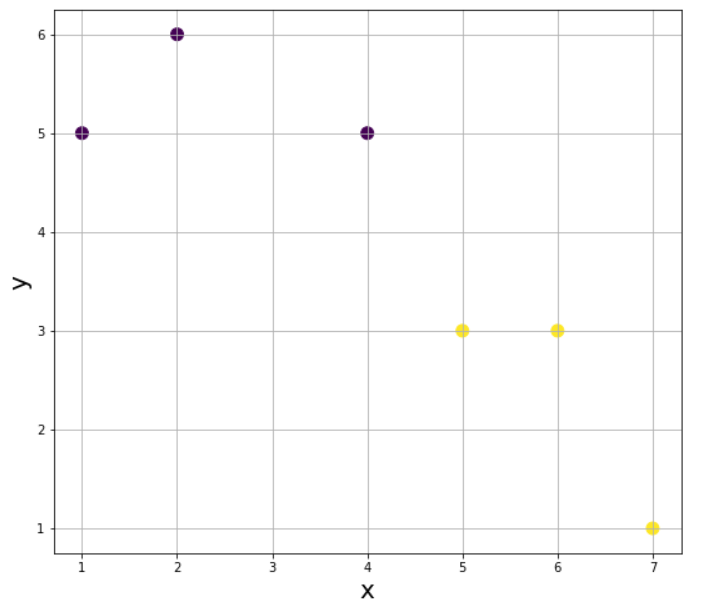
여기서 새로운 데이터 (4, 4)가 입력되었다고 하자. 그럼 이 데이터는 레이블 0(보라색)과 1(노란색) 중에서 어떤 값으로 분류가 될까? 앞서 살펴본 K-NN 알고리즘의 정의에 따라 거리를 기반으로 가장 가까운 K개의 이웃의 값을 참고하여야 한다. 그러기 위해 먼저 K의 값을 지정해야한다.

1) K = 1

K가 1인 경우 입력된 데이터로 부터 가장 가까운 한 개의 데이터의 특성을 참고하면 된다.

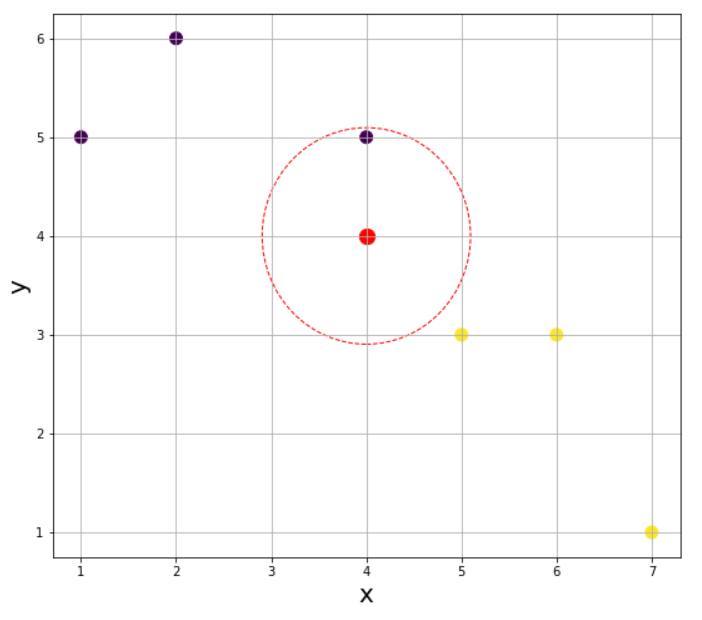
새로운 데이터인 빨간색 점으로 부터 같은 거리에 있는 점들을 이어 원을 그었을 때 그 원에 들어오는 점이 한 개일때 위와 같은 그림이 나온다. 가장 가까운 이웃의 점의 색이 보라색이 이라서 K-NN 알고리즘에 따라 레이블 0(보라색)으로 분류된다.

2) K = 2

K가 2인 경우 가장 가까운 이웃의 수를 2개까지 늘리면 된다.

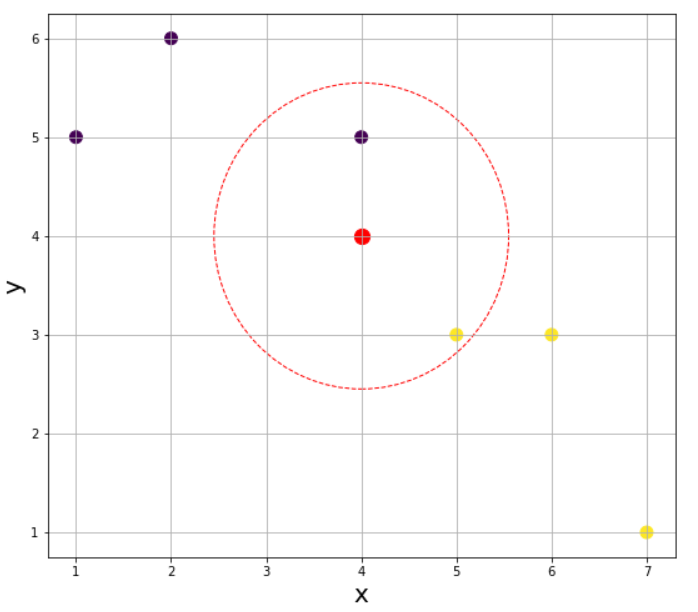
하지만 이때 문제가 발생한다. 가장 가까운 이웃이 각각 1개씩 나와 어떤 값으로 분류해야할지 알 수 없는 상황이다. 물론 가장 가까운 이웃을 따르거나 랜덤으로 찍어도 되지만 편의상 보편적으로 K의 값을 정할 때 동률이 나오지 않도록 홀수로 지정한다. K가 3인 경우로 넘어가자.

3) K = 3

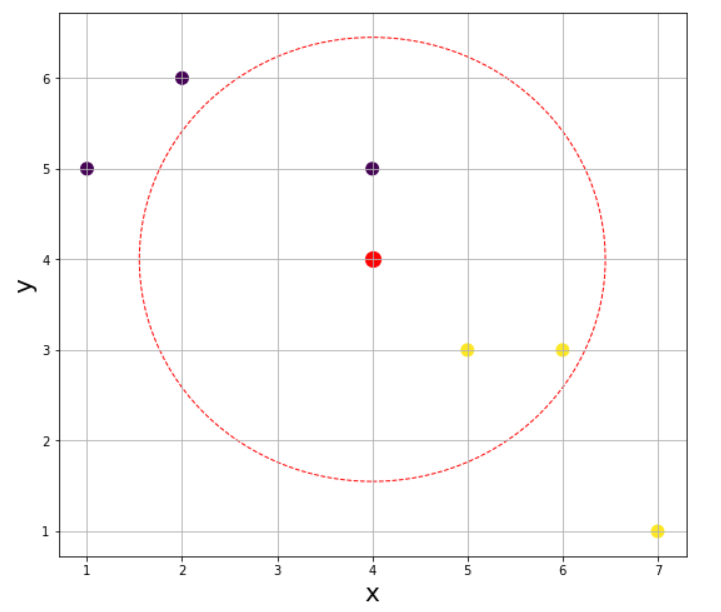
이번에는 K가 1인 경우와 다르게 가장 가까운 3개의 점을 확인하였을 때 노란색 점의 개수가 더 많으므로 레이블 1(노란색)로 분류될 것이다. K가 4인 경우는 동률이 나올 수 있으니(실제로 동률이 나온다.) 패스하고 K가 5인 경우를 확인해보자.

4) K = 5

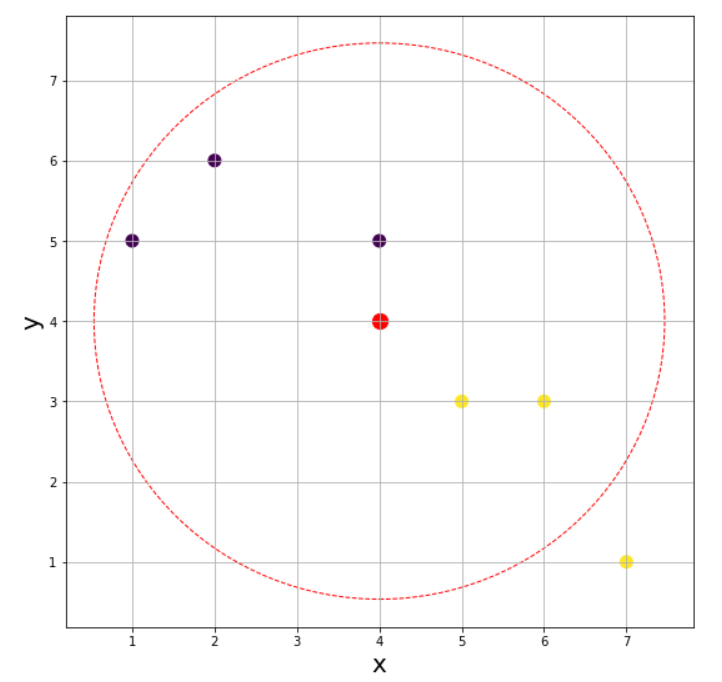
이번엔 또다시 레이블 2(보라색)으로 분류된다. K의 값에 따라 참고하는 데이터의 개수가 달라지고 그럼 분류되는 레이블이 달라지는 것을 알 수 있다. 즉, K의 값에 따라 결과가 달라지며 따라서 잘 지정해주어야 한다는 것을 명심해야한다. 물론 데이터의 개수가 많아지면 이 정도로 레이블이 변덕스럽게 바뀌지는 않을 것이다.

K-NN 알고리즘의 구현 시 주의점

K-NN 알고리즘을 구현할 때 주의해야할 점이 있다. K-NN 알고리즘과 같은 거리기반 모델의 경우에는 구현 시 변수 값의 범위를 재조정 해주어야 한다. 거리를 잴 때에는 숫자를 다루므로 변수 값 범위 재조정를 해주어야 변수의 중요도를 고르게 해석할 수 있다. 참고로 K-means 알고리즘도 비지도학습에 포함되는 거리기반 분류 알고리즘이라서 마찬가지로 변수 값 범위 재조정이 필요하다. (위에서 보았던 'K-NN 알고리즘의 원리'의 예시는 변수의 범위가 비슷했으므로 범위 조정이 필요하지 않았다.)

변수 값 범위 재조정을 해야하는 이유?

변수 값 범위 재조정을 해야 하는 이유에 대해 쉽게 이해하기 위해 예시를 하나 들어보자. 평균 기온과 평균 강수량에 따른 우리나라의 지역별 분류를 한다고 해보자.

이미지 출처 : http://study.zum.com/book/13852

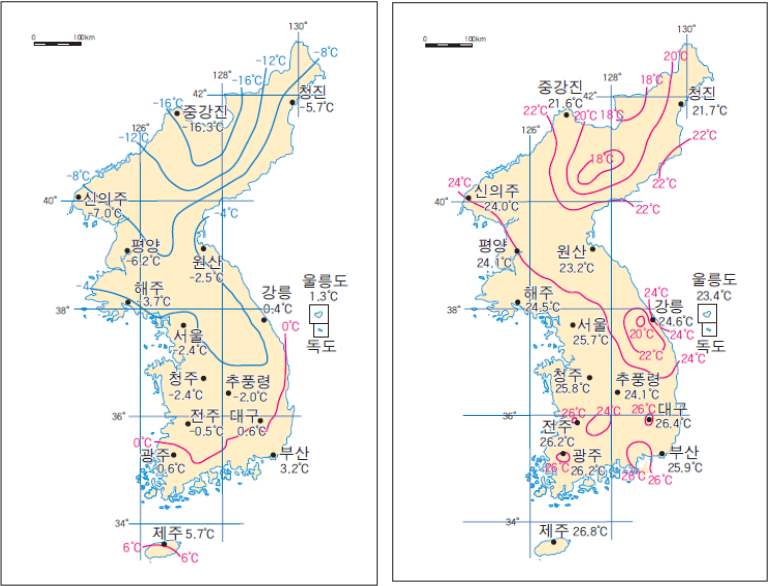
위의 왼쪽 그림은 겨울철 우리나라 평균 기온을 나타낸 지도이고 오른쪽 그림은 여름철 우리나라 평균 기온을 나타낸 지도이다.
기온의 변화 폭을 보면 서울의 경우 -2.4도에서 25.7도 정도이다. 평균 기온에 따라 분류를 하게된다면 여름이든 겨울이든 위도에 따라 크게 위쪽과 아래쪽으로 분류가 될 것이다.

이미지 출처 : http://study.zum.com/book/15165

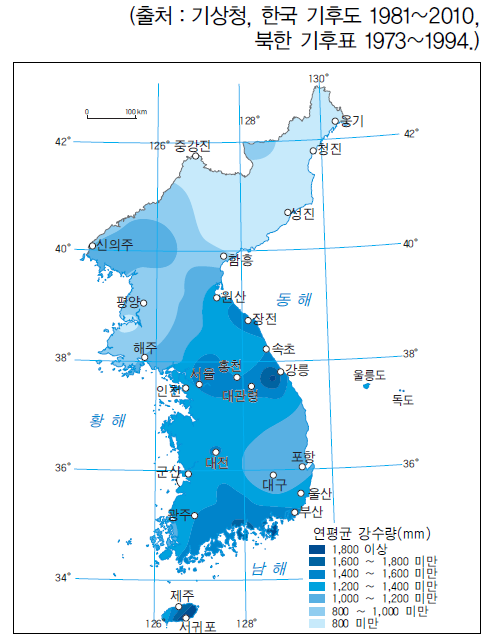
위의 그림은 우리나라의 연평균 강수량 정보를 나타낸 지도이다. 강수량 값을 보면 평균 기온과 다르게 위도가 그렇게 크게 영향을 미치지는 않는다.

여기서 주목해야할 점은 평균 기온은 10단위를 넘지 않는 반면 강수량의 경우 1000단위에 다다르는 지역도 있다는 것이다. 거리를 기반으로 분류를 하다보면 수치적으로 큰 강수량 값에 초점을 맞춰 분류를 하게 될 것이다. 즉, 분류 모델이 상대적으로 큰 값을 지니는 강수량 값은 중요하게 고려하고 상대적으로 값이 작은 평균 기온은 무시하는 경향을 보일 것이다. 결국 평균 기온과 강수량 두 변수를 독립변수로 두는 이유가 상실된다. 이는 단위(범위)를 맞춰주지 않아서이며 범위 재조정이 꼭 필요한 이유이다. 대략 1000단위를 지니는 강수량과 대략 10단위를 지니는 평균기온을 비슷한 단위로 조정을 해주어야 한다.

변수 값 범위 재조정 방법

K-NN 알고리즘을 사용하기 위해 각 변수들의 범위를 재조정해야하는데 이에는 크게 2가지 방법이 있다.

1. 최소-최대 정규화(min-max normalization)
2. z-점수 표준화(z-score standardization)
   
   

최소-최대 정규화(min-max normalization)

최소-최대 정규화는 변수의 범위를 0%에서 100%까지로 나타낸다. 공식은 다음과 같다.

z-점수 표준화(z-score standardization)

z-점수 표준화는 변수의 범위를 정규분포화하여 평균을 0, 포준편차가 1이 되도록 한다. 공식은 다음과 같다.

K-NN 알고리즘 구현하기(iris 데이터)

유명한 iris 데이터로 간단히 K-NN 알고리즘을 사용하여 분류를 해보자.

import numpy as np
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split

iris = load_iris()

knn = KNeighborsClassifier(n_neighbors = 3)

X_train, X_test, Y_train, Y_test = train_test_split(iris['data'], iris['target'], test_size=0.25, stratify = iris['target'])

Y_train

knn.fit(X_train, Y_train)

<실행 결과>
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=None, n_neighbors=3, p=2,
weights='uniform')

y_pred = knn.predict(X_test)

print("prediction accuracy: {:.2f}".format(np.mean(y_pred == Y_test)))

<실행 결과>
prediction accuracy: 0.97

---

참고 :
https://kkokkilkon.tistory.com/14
http://aikorea.org/cs231n/classification/#knn
https://m.blog.naver.com/bestinall/221760380344